LÖSUNGEN MIT R Aufgabe 1 (Grundaufgabe W1) Präzisierung der

ANGEWANDTE STATISTIK 1
MUSTERBEISPIELE MIT LÖSUNGEN
GRUNDAUFGABEN ZUM RECHNEN MIT WAHRSCHEINLICHKEITEN
1. Bei der Bearbeitung eines Problems sind 5 voneinander unabhängige Entscheidungen zu treffen,
von denen jede einzelne mit der Wahrscheinlichkeit α = 0,05 eine Fehlentscheidung sein kann.
Man bestimme die simultane Irrtumswahrscheinlichkeit α_g, d.h. die Wahrscheinlichkeit, dass
eine oder mehr als eine der Entscheidungen falsch sind.
2. Bei einem Verfahren zur sterilen Abfüllung von Flaschen tritt mit der Wahrscheinlichkeit p=0,1%
ein Ausschuss (unsterile Flasche) auf. Es werden n Flaschen zufällig aus einem (sehr großen)
Produktionslos entnommen (Prüfstichprobe). Wie viele Flaschen müssen zur Prüfung vorgesehen
werden, damit mit mindestens 95%iger Sicherheit in der Prüfstichprobe (wenigstens) eine
unsterile Flasche auftritt?
3. In einem Unternehmen mit 500 Beschäftigten werden im Zuge einer Grippeimpfung 300 geimpft.
In der Folge erkrankten 50 Personen, von denen 15 geimpft waren. Wie groß ist die
Wahrscheinlichkeit dafür, dass a) eine Person erkrankt, b) eine geimpfte Person erkrankt, c) eine
erkrankte Person zur Gruppe der Geimpften gehört?
4. Bei einem diagnostischen Verfahren zum Nachweis einer Erkrankung sei die Wahrscheinlichkeit,
ein falsch-positives (falsch-negatives) Ergebnis zu erhalten, gleich 0,5% (2,5%). Die
Wahrscheinlichkeit für das Auftreten der Krankheit in einer bestimmten Zielgruppe sei 1,5%. Man
berechne die Wahrscheinlichkeit, dass bei positivem Ergebnis tatsächlich eine Erkrankung
vorliegt.
LÖSUNGEN MIT R
Aufgabe 1 (Grundaufgabe W1)
Präzisierung der Aufgabe:
F1, F2, F3, F4, F5 bezeichnen die Ereignisse, dass die erste, zweite, …, fünfte Entscheidung falsch ist.
Gemäß Angabe ist P(F1)=P(F2) = P(F3) = P(F4)=P(F5) =α = 0,05.
Gesucht: P(F1 oder F2 oder F3 oder F4 oder F5)
Lösungsansatz:
F1, F2, F3, F4 und F5 sind einander nicht ausschließende Ereignisse, so dass die Additionsregel für
einander ausschließende Ereignisse nicht angewendet werden kann. Es empfiehlt sich, zu den
Gegenereignissen R1, R2, R3, R4 bzw. R5 überzugehen, die die Ereignisse darstellen, dass die erste,
zweite, …, fünfte Entscheidung richtig ist. Es gilt P(R1) = P(R2) = P(R3) =P(R4)=P(R5)=1 − α. Auf
Grund der Unabhängigkeit der Entscheidungen sind die Ereignisse R1, R2, R3, R4 und R5 paarweise
voneinander unabhängig. Wegen
P(F1 oder F2 oder F3 oder F4 oder F5)=1-P(R1 und R2 und R3 und R4 und R5)=
1-P(R1) P(R2) P(R3)P(R4)P(R5)=1-(1 - α)5 =1-0,955=22,62%
Rechnerische Lösung (mit R):
>
+
>
>
>
alpha_g <- function(alpha,n) {
1 - (1-alpha)^n}
n <- 5
alpha <- 0.05
print(cbind(n, alpha_g(alpha, n)), digits=4)
n
[1,] 5 0.2262
Ergebnis:
Die Wahrscheinlichkeit beträgt 22,62%, dass von 5 unabhängigen Entscheidungen mindestens eine
falsch ist, wenn das Fehlerrisiko für die Einzelentscheidung 5% ist.
Musterbeispiele_STAT1_mit_Loesungen
1
ANGEWANDTE STATISTIK 1
MUSTERBEISPIELE MIT LÖSUNGEN
Aufgabe 2 (Grundaufgabe W2)
Präzisierung der Aufgabe:
Das Produktionslos wird als sehr groß vorausgesetzt; der Ausschussanteil (d.h. die
Wahrscheinlichkeit, durch Zufallsauswahl eine defekte Einheit zu erhalten, ist p=0,1%. Wenn das
Produktionslos sehr groß im Vergleich zur Prüfstichprobe ist, kann der Auswahlvorgang als ein
„Ziehen mit Zurücklegen“ modelliert werden. Gesucht ist der Umfang der Prüfstichprobe, so dass
in der Prüfstichprobe mit 95%iger Wahrscheinlichkeit mindestens eine defekte Einheit auftritt.
Lösungsansatz:
Es sei X die Anzahl der defekten Einheiten in der Prüfstichprobe und n der (zu bestimmende) Umfang
der Prüfstichprobe. Nach Voraussetzung ist n klein im Vergleich zur Größe des Produktionsloses. Die
Prüfstichprobe kann man sich unter dieser Voraussetzung so erzeugt denken, dass n-mal eine Einheit
aus dem Produktionslos aufs Geratewohl ausgewählt wird und bei jedem Auswahlvorgang die
Wahrscheinlichkeit p für die Auswahl einer defekten Einheit gleich p=0,001 ist. Die
Wahrscheinlichkeit eine intakte Einheit auszuwählen, ist 1-p = 0.999; die Wahrscheinlichkeit
insgesamt n intakte Einheiten auszuwählen, ergibt sich aus der Multiplikationsregel für unabhängige
Ereignisse zu P(X=0)= (1-p)n = 0.999n. Das Gegenereignis zu „n intakte Einheiten auszuwählen“ ist
das Ereignis „mindestens eine defekte Einheit auszuwählen“; die Wahrscheinlichkeit dafür ist
P(X>=1)= 1-P(X=0) = 1-0.999n. Gesucht ist n derart, dass P(X>=1) = 1-0,999n = 0.95 ist.
Rechnerische Lösung (mit R):
Die Lösung der Gleichung 1-0,999n = 0.95 wird durch „Einsetzen“ von Werten für n gefunden.
>
>
>
+
+
+
>
options(digits=4)
n <- 1
repeat{
P <- 1-0.999^n
if (P >= 0.95) break
n <- n+1}
print(cbind(n, P))
n
P
[1,] 2995 0.95
Ergebnis:
Für die Prüfstichprobe ist ein Mindestumfang von n= 2995 zu planen, damit – bei einem Fehleranteil
von 0,1% - mit einer Sicherheit von (zumindest 95%) mindestens eine fehlerhafte Einheit „gezogen“
wird.
Aufgabe 3 (Grundaufgabe W3)
Präzisierung der Aufgabe:
Es sei E das Ereignis, dass einer der 500 Beschäftigen an Grippe erkrankt, und G das Ereignis, dass
einer der Beschäftigten geimpft wird. Gesucht ist in Teilaufgabe a) die (unbedingte)
Wahrscheinlichkeit P(E), in Teilaufgabe b) die bedingte Wahrscheinlichkeit P(E|G) und in
Teilaufgabe c) die Wahrscheinlichkeit P(G|E).
Lösungsansatz und rechnerische Lösung:
a) P(E) = 50/500 = 10% (Laplace-Definition der Wahrscheinlichkeit)
b) P(E|G) = P(E und G)/P(G) = (15/500)/(300/500) = 5% (Definitionsgleichung der bedingten
Wahrscheinlichkeit)
c) P(G|E) = P(E und G)/P(E) = (15/500)/(50/500) = 30%
Ergebnis:
Die unbedingte Wahrscheinlichkeit für eine Erkrankung ist 10%, die Wahrscheinlichkeit der
Erkrankung einer geimpften Person beträgt 5% und die Wahrscheinlichkeit, dass eine erkrankte Person
vorher geimpft wurde, ist 30%.
Musterbeispiele_STAT1_mit_Loesungen
2
ANGEWANDTE STATISTIK 1
MUSTERBEISPIELE MIT LÖSUNGEN
Aufgabe 4 (Grundaufgabe W4)
Präzisierung der Aufgabe:
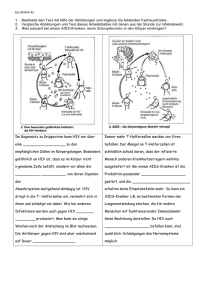
Es sei HIV+ das Ereignis, dass eine aus der Zielpopulation aufs Geratewohl ausgewählte Person HIVinfiziert ist; die Wahrscheinlichkeit dieses Ereignisses ist laut Angabe P(HIV+)= 1,5%. Die
Wahrscheinlichkeit des Gegenereignisses HIV- (ausgewählte Person ist nicht HIV-infiziert) beträgt
P(HIV-) = 1-P(HIV+)=98,5%. Ein falsch-positives Ergebnis liegt vor, wenn eine gesunde Person
einen positivem Testbefund hat. Die Wahrscheinlichkeit dieses Ereignisses kann durch die bedingte
Wahrscheinlichkeit P(T+|HIV-) ausgedrückt werden. Ein falsch-negatives Ergebnis liegt vor, wenn
eine HIV-infizierte Person einen negativen Testbefund hat; die Wahrscheinlichkeit dieses Ereignisses
ist P(T-|HIV+). Gesucht ist die Wahrscheinlichkeit P(HIV+|T+) dafür, dass eine Person mit positivem
Testbefund tatsächlich HIV-infiziert ist.
Lösungsansatz und Lösung:
Variante 1 (Lösung mit Bayes’scher Formel):
Mit bekannter Sensitivität P(HIV+|T+) und Spezifität P(HIV-|T-) des diagnostischen Tests sowie der a
priori-Wahrscheinlichkeit P(HIV+) kann die gesuchte Wahrscheinlichkeit kann mit der Bayes’schen
Formel in Form
P(HIV+ | T +) =
P (T + | HIV+) P (HIV+)
P(T + | HIV+) P(HIV+) + P (T + | HIV-)P (HIV-)
dargstellt werden. Aus der Angabe ist bekannt:
P(HIV+)=0,015; P(HIV-)=0,985;
P(T+|HIV-)= 0,005; P(T-|HIV-)=1-P(T+|HIV-)=0,995
P(T-|HIV+)=0,025; P(T+|HIV+)=1-P(T-|HIV+)=0,975
Einsetzen in die Bayes’sche Formel liefert:
P(HIV+|T+)=0,975*0,015/[0,975*0,015 + 0,005*0,985] = 0,748
Variante 2 (Lösen mit der Laplace’sche Wahrscheinlichkeitsdefinition nach Übergang zu absoluten
Häufigkeiten):
Gegeben:
P(T+ | HIV-) =
P(T- | HIV+) =
P(HIV+) =
Gesucht:
P(HIV+|T+)
0,005
0,025
0,015
P(T- | HIV-) =
P(T+ | HIV+) =
P(HIV-)=
Berechnung: mittels Übergang zu absoluten Häufigkeiten;
Anzahl der Personen in der Zielgruppe =
0,995
0,975
0,985
1.000.000
1.000.000
HIV+
15000
T+
14625
P(HIV+ | T+)=
HIV985.000
T375
T+
4925
T980.075
0,7481
Ergebnis:
Die Wahrscheinlichkeit P(HIV+|T+) bei positivem Testbefund tatsächlich HIV-infiziert zu sein,
beträgt 74,8%.
Musterbeispiele_STAT1_mit_Loesungen
3