Übungsblatt 4 Versicherung und Risikoverhalten

Mikroökonomik B - SoSe2011
Übungsblatt 4 - Seite 1 von 2
Übungsblatt 4
Versicherung und Risikoverhalten
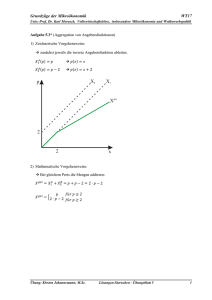
Aufgabe 4.1 Versicherung und Risikoteilung
In einer Agrarökonomie steht ein Bauer B einem Elementarrisiko gegenüber. Mit Wahrscheinlichkeit p bricht ein Feuer auf seinem Hof aus und die Scheune brennt ab. B hat
ein Einkommen von w0 und der Wiederaufbau der Scheune verursacht Kosten, die einem
monetären Betrag k < w0 entsprechen. Bs Präferenzen haben die Erwartungsnutzeneigenschaft und lassen sich durch folgende Nutzenfunktion abbilden:
u(w) = ln(w).
Es wird eine Feuerversicherung angeboten: Für eine zustandsunabhängige Zahlung von
γx (Versicherungsprämie) bekommt der Bauer eine Auszahlung von x falls ein Feuer
ausbricht.
(a) Stellen Sie Bs Optimierungsproblem auf und bestimmen Sie Bs Nachfrage nach
Versicherung abhängig von γ.
Nach einer (in diesem Teil der Vorlesung) unerklärlichen Häufung von Feuersbrünsten
findet sich keine zahlungsfähige Versicherungsgesellschaft mehr. Bs Nachbar C steht vor
demselben (aber unabhängigen) Feuerrisiko wie B und hat gleiche Nutzenfunktion und
gleiches Einkommen wie B. B und C überlegen, folgenden Vertrag zu schließen: Alle
feuerbedingten Wiederaufbaukosten bei B und C werden von beiden geteilt, wobei B
einen Anteil β ∈ [0; 1] und C den Rest der gesamten Aufbaukosten trägt.
(b) Bestimmen Sie die durch den Vertrag induzierten Einkommenlotterien für B und
C.
(c) Zeigen Sie, dass ein Vertrag mit β = 1/2 sowohl B als auch C besser stellt als kein
Vertrag.
(d) Nehmen Sie jetzt an, dass p = 2/3 und w0 = (4/3)k.
Für welches β ist C gerade indifferent den Vertrag anzunehmen?
Aufgabe 4.2 Risikoverhalten I
Bauer B hat 1000 Hennen, die jeden Tag jeweils ein Ei legen. Er kann die Eier für den
Preis von 10 Cent pro Ei auf dem Markt verkaufen. Der Eierverkauf ist Bs einzige Ein√
nahmequelle und seine indirekte Nutzenfunktion ist y. Dabei gibt y B’s Einnahmen an.
Jeden Tag trägt B seine Eier auf den Markt. Der Weg ist jedoch steinig, mit 50% Wahrscheinlichkeit stürzt der Bauer und alle Eier in seinem Korb zerbrechen und können nicht
mehr verkauft werden.
(a) Angenommen B hat keine Opportunitätskosten der Zeit, würde B lieber einmal mit
allen 1000 Eier gehen oder zweimal mit jeweils 500 Eiern? (Nehmen Sie an, daß
Stürze unabhängige Ereignisse sind.)
Mikroökonomik B - SoSe2011
Übungsblatt 4 - Seite 2 von 2
Aufgabe 4.3 Risikoverhalten II
Schwarzfahrer S bezieht Nutzen aus seinem monetärem Einkommen x gemäß der indirekten Nutzenfunktion u(x) = − exp{−x}. S verfügt über (hinreichend große) monatliche Mittel m. Der Preis für Bahnfahrten beträgt p Euro pro Fahrt. Mit Wahrscheinlichkeit
q wird S auf einer Fahrt kontrolliert. Falls S keine gültige Fahrkahrte besitzt, muß er eine
Strafe in Höhe von t zahlen.
(a) Vor dem Einsteigen entscheidet S über den Kauf einer gültigen Fahrkarte. Berechnen Sie die Kontrollwahrscheinichkeit q, so dass S genau indifferent ist zwischen
Fahrkartenkauf und Schwarzfahrt. Wird S bei den Parameterwerten p = 2, t = 3p
und q = 0, 01 schwarzfahren?
Nehme Sie an, S unternimmt pro Monat 2 Fahrten und die Kontrollen sind statistisch
unabhängig. Weiterhin seien p = 2 und t = 3p.
(b) Wie viele Fahrkarten wird S kaufen, wenn q = 0, 01? (Definieren Sie zuerst die
Lotterien, zwischen denen S auswählen kann, stellen Sie S’ Optimierungsproblem
auf, und bestimmen Sie dann die optimale Lotterie.)
(c) Wie ändert sich die optimale Anzahl, falls sich S’ monatliche Mittel m verändern?
Argumentieren Sie, eine Rechnung ist nicht erforderlich.
(d) (schwieriger) Nun sei die Kontrollwahrscheinlichkeit q eine Funktion der kontrollierten Züge z, q(z) = z/Z, 0 ≤ z ≤ Z, wobei Z die Anzahl der fahrenden Züge
beschreibt. Einen Zug zu kontrollieren, verursacht positive Kosten. Berechnen Sie
die kostenminimierende Kontrollwahrscheinlichkeit q, so dass S den Kauf von 2
Fahrkarten gegenüber 2 Schwarzfahrten mindestens schwach bevorzugt. Es fahren
so viele Züge , dass q als stetige Variable betrachtet werden kann. Formulieren Sie
eine Gleichung, die neben q keine weiteren Parameter oder Variablen enthält und
deren Lösung dem gesuchten q entspricht. Das Auflösen der Gleichung ist nicht
notwendig.