blatt12a - Physik

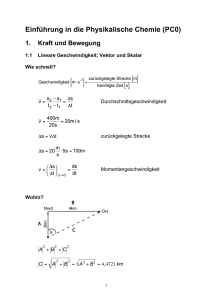
Übungen Physik für Bauingenieurwesen WS01/02
Prof. Dr. P.Böni
Blatt 12
Sergey Prokudaylo
Besprechung am Di, 22.1.2002 (N 0825 14.30) im Hörsaal 1200.
http://www.ph.tum.de/antares/uebungen/uebungen.html
Aufgabe 1: Seilwelle
Eine Seilwelle mit der Wellenlänge , der Frequenz f und der Amplitude A läuft in positiver xRichtung. Zur Zeit t1 befindet sich bei x1 ein Wellental. Stellen Sie die Funktion A(t,x) für
diese Welle auf.
, f, Amin, t1 = T/2, x1 = ¾ .
Aufgabe 2: Entfernung von Sternen
Auf der Erde wird die -Linie der Balmer-Serie des Wasserstoffs mit einer Frequenz von  =
3.5 1014 Hz ( = 4.57 1014 Hz) gesehen. Mit welcher Geschwindigkeit bewegt sich der Stern
von der Erde weg ? Wie groß ist seine Beschleunigung bezüglich der Erde, wenn man
annimmt, daß er beim Urknall mit der gleichen Anfangsgeschwindigkeit wie dei Erde vom
selben Punkt aus ins Weltall geschleudert wurde (Alter des Welltalls : 1010 Jahre)? Welchen
Abstand hat er von der Erde? ( alle Rechnungen nicht relativistisch)
Aufgabe 3: Dynamik einer Feder
Längs einer Schraubenfeder bewegt sich eine Longitudinalwelle mit der Geschwindigkeit
4m/s. Der Abstand zwischen je zwei aufeinanderfolgenden Verdichtungen ist 80 cm, die von
den Teilchen erreichte Amplitude 3 mm. Wie gross ist die Geschwindigkeitsamplitude?
Welche Energie besitzt ein Massenelement von 0.016 g auf der schwingenden Feder?
Aufgabe 4: Superposition periodischer Wellen
Längs eines Drahtes breiten sich zwei Transversalwellen in derselben (positiven x-Richtung)
mit gleicher Amplitude und Frequenz aus. Infolge der 1. Welle geht das Teilchen im 0-Punkt
der Achse zur Zeit t = 0 in der positiven y-Richtung durch die Gleichgewichtslage. Die 2.
Welle läuft mit einem Gangunterschied von ¼ Wellenlänge hinter der ersten nach. Wie lautet
die Schwingungsgleichung für ein beliebiges Teilchen? Berechne damit die resultierende
Elongation für verschiedene Abszissen- und Zeitwerte, z.B. für x =  und t = T.