kapitel2_aufgaben
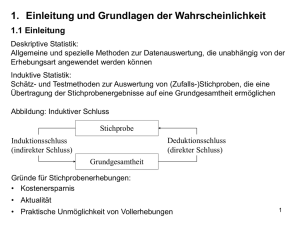
Werbung
Zufallsexperimente; Ergebnisräume
1. Nenne wesentlichen Merkmale durch die sich Zufallsexperimente von
physikalischen Experimenten unterscheiden.
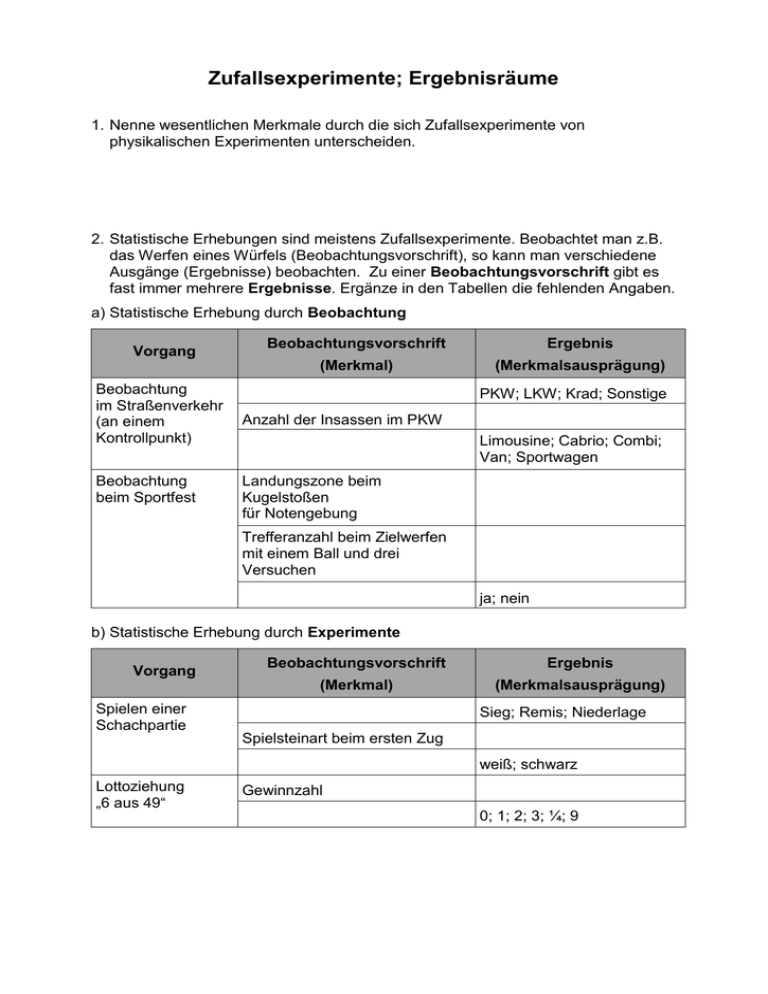
2. Statistische Erhebungen sind meistens Zufallsexperimente. Beobachtet man z.B.
das Werfen eines Würfels (Beobachtungsvorschrift), so kann man verschiedene
Ausgänge (Ergebnisse) beobachten. Zu einer Beobachtungsvorschrift gibt es
fast immer mehrere Ergebnisse. Ergänze in den Tabellen die fehlenden Angaben.
a) Statistische Erhebung durch Beobachtung
Vorgang
Beobachtung
im Straßenverkehr
(an einem
Kontrollpunkt)
Beobachtung
beim Sportfest
Beobachtungsvorschrift
Ergebnis
(Merkmal)
(Merkmalsausprägung)
PKW; LKW; Krad; Sonstige
Anzahl der Insassen im PKW
Limousine; Cabrio; Combi;
Van; Sportwagen
Landungszone beim
Kugelstoßen
für Notengebung
Trefferanzahl beim Zielwerfen
mit einem Ball und drei
Versuchen
ja; nein
b) Statistische Erhebung durch Experimente
Vorgang
Beobachtungsvorschrift
Ergebnis
(Merkmal)
(Merkmalsausprägung)
Spielen einer
Schachpartie
Sieg; Remis; Niederlage
Spielsteinart beim ersten Zug
weiß; schwarz
Lottoziehung
„6 aus 49“
Gewinnzahl
0; 1; 2; 3; ¼; 9
3. Bei einer statistischen Erhebung werden Familien mit vier Kindern befragt. Die
Auswertung der Antworten erfolgt nach unterschiedlichen Gesichtspunkten.
Formuliere für die angegebenen Ergebnismengen jeweils mögliche Fragen
hinsichtlich der bei dieser Umfrage interessierenden Merkmale.
a)
= {(M; M; M; M); (M; M; M; W); (M; M; W; M); (M; M; W; W); (M; W; M; M);
(M; W; M; W); (M; W; W; M); (M; W; W; W); …; (W; W; W; W)}
b)
= {{M; M; M; M}; {M; M; M; W}; {M; M; W; W}; {M; W; W; W};
{W; W; W; W}}
c)
= {ja; nein}
d)
= {0; 1; 2}
e)
= {0; 1; 2; 3; 4}
4. Die Elemente der Ergebnismengen von Zufallsexperimenten können sehr
unterschiedlicher Art sein: Zahlen, Größen, geordnete Paare von qualitativen
Ausdrücken usw.
Nenne analog zum Beispiel zu den unter a) bis e) gegebenen Arten der Elemente
jeweils einen möglichen zugrunde liegenden Vorgang und ein interessierendes
Merkmal. Gib die zugehörige Ergebnismenge an.
Beispiel:
natürliche Zahl
Vorgang/Merkmal:
Auswahl eines Schülers der Klasse mithilfe
der Nummerierung im Klassenbuch
Ergebnismenge:
W = {1; 2; 3; ¼; 29; 30}
a)
Längenmaß
Vorgang/Merkmal:
Ergebnismenge:
b)
Zeitintervall
Vorgang/Merkmal:
c)
Ergebnismenge:
qualitativer Ausdruck
Vorgang/Merkmal:
Ergebnismenge:
d)
Wahrheitswert
Vorgang/Merkmal:
Ergebnismenge:
dreielementige Mengen
e)
Vorgang/Merkmal:
Ergebnismenge:
Ergebnis und Ereignis
Für eine Feier wird ein Lotto „2 aus 5“ vorbereitet. Aus einem Säckchen mit fünf
Kugeln, die mit den Zahlen 1 bis 5 beschriftet sind, kann ein Mitspieler nacheinander
zwei Kugeln – ohne zurückzulegen – ziehen.
Beim Spiel gibt es Preise zu gewinnen, wenn die folgenden Bedingungen erfüllt sind:
Hauptgewinn
Die zweite Zahl ist die Quadratzahl der ersten (Ereignis H).
Trostpreis 1
Beide Zahlen sind ungerade (Ereignis E).
Trostpreis 2
Die erste Zahl ist um 1 kleiner als die zweite (Ereignis Z).
Trostpreis 3
Die zweite Zahl ist größer als die erste (Ereignis D).
a)
Welche Ergebnisse sind bei dieser Lotto-Ziehung möglich? Gib die
Ergebnismenge an.
b)
Welche jeweiligen Teilmengen (Ereignisse) aus der Ergebnismenge sind
den Preisen zugeordnet?
Hauptgewinn:
Trostpreis 1:
Trostpreis 2:
Trostpreis 3:
c)
Gib die Menge der Ergebnisse an, denen kein Preis zugeordnet ist
(Ereignis N).
d)
Stelle die Beziehungen zwischen den Ereignissen (Mengen) E, Z und D in
einem Venndiagramm (Mengendiagramm) dar.
Gib die Menge der Ziehungsergebnisse an, bei denen man zwischen zwei
Trostpreisen auswählen kann.
NOCH EINIGE KURZE AUFGABEN
Ergebnisräume
Gib für die folgenden Situationen einen Ergebnisraum an!
1.
a)
b)
c)
d)
e)
Welche Zahl fällt beim nächsten Roulettespiel
Welches Geschlecht wird das Neugeborene haben?
Welche Note bekomme ich in der nächsten Klausur?
Welches Alter werde ich erreichen?
Welche Seiten werden oben liegen, wenn ich gleichzeitig einen Pfennig und
einen Groschen werfe?
f) Eine Münze wird so lange geworfen, bis zum ersten mal Kopf fällt, höchstens
jedoch 8 mal.
Ereignisräume
2. Stelle folgende Ereignisse beim Wurf eines Würfels als Mengen dar!
a)
b)
c)
d)
3.
Ein Würfel wird zweimal geworfen. Stelle die folgenden Ereignisse als
Teilmenge des Ergebnisraumes dar!
a)
b)
c)
d)
4.
„Augenzahl ist kleiner 3“
„Augenzahl ist größer als drei und kleiner als fünf“
„Augenzahl ist größer gleich eins“
„Augenzahl ist keine Primzahl“
Die Augensumme beträgt höchstens fünf.
Die Augensumme ist gerade.
Das Produkt der Augenzahlen beträgt 12.
Das Produkt der Augenzahlen beträgt mindestens 7.
Ein Würfel wird einmal geworfen.
E1 sei das Ereignis: “Die Augenzahl ist kleiner 3.“, E2 bedeutet das
Ereignis: “Die Augenzahl ist eine ungerade zahl.“. Ermittle die folgenden
Ereignisse. Welch Ereignisse sind gleich?
a) E1 E2
b) E1 E2
c) E1 E2
d) E1 E2
e) E1 E2
f ) E1 E2
g) E1 E2
h) E1 E2
i) E1 E2
j) E1 E2