Ergebnis, Ergebnismenge, Ereignis

Aufgabe 2.1
Ergebnis, Ergebnismenge, Ereignis
Ergebnis und Ergebnismenge
Vorgänge mit zufälligem Ergebnis, oft „Zufallsexperiment“
genannt
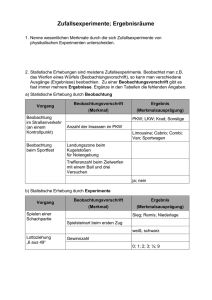
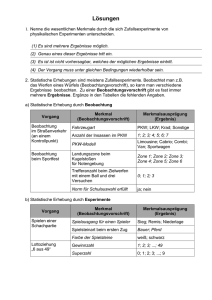
Bei der Beschreibung der Ergebnisse wird stets ein
bestimmtes Merkmal des Zufallsexperiments benannt.
Zufallsexperiment
Merkmal
Ergebnisse
Hochsprung von
Schülern
Sprunghöhe
Höhen zwischen
0,75m und 1,70 m
Ziehen von Kugeln
aus Urne
Werfen einer Münze
gelb, grün, blau
Lage der Oberseite
der Münze
Werfen eines Würfels
Kontrolle einer
Bonbontüte
24,25,26,27,28
Beispiel: Würfeln mit einem Würfel
Mögliche Ergebnismenge,
je nach Fragestellung:
Ω1 = {1,2,3,4,5,6, Ecke, Kante}
Die Ergebnismenge Ω
(sprich:“Omega“)
enthält alle möglichen
Ergebnisse eines
Zufallsexperiments.
Ω2 = {1,2,3,4,5,6}
Ω3 = {6, keine 6}
Ω4 = {gerade, ungerade Augenzahl}
Welche Ergebnismenge
erscheint am geeignetsten d. h. nicht zu grob und ohne
überflüssige Ergebnisse für die Frage nach der
Wahrscheinlichkeit einer
Augenzahl? Begründe.
Die Ergebnisse sind
also die Elemente der
Keine Ergebnismenge:
Ergebnismenge.
Ω = {gerade Zahlen oder
Primzahlen kleiner gleich 6}
Sie sollen höchstens einmal
in Ω vorkommen.
Warum?
Nenne einen geeigneten Ergebnisraum für die folgenden
Zufallsexperimente:
1. Würfeln eines Tetraeders mit den Augenzahlen 1,2,3 und 4.
2. Beim Werfen zweier Tetraederwürfels („zweistufiges
Zufallsexperiment“)
bietet jemand folgende Ergebnismengen an:
Bemerkung: Das Ergebnis (3|4) bedeutet, dass im ersten Wurf eine 3 und im zweiten
Wurf eine 4 gewürfelt wird.
Ω1 = {(1|1);(1|2),(1|3),(1|4), (2|1);(2|2),(2|3),(2|4),(3|1);(3|2),(3|3),(3|4),(4|1);(4|2),(4|3),(4|4)}
Ω2 = {(1|1);(1|2),(1|3),(1|4),(2|2),(2|3),(2|4),(3|3),(3|4),(4|4)}
Ω2 = {Augensumme größer als 1 und kleiner als 9}
Welches sind Ergebnismengen des Experiments?
3. In einer Klinik wir eine Statistik über das Geschlecht der
Neugeborenen geführt.
a) Einzelkinder
b) eineiige Zwillinge
c) zweieiige Zwillinge
Aufgaben
1. Bei einem Wettrennen starten die vier Personen A,B,C und D. Man geht davon
aus, dass alle Läufer zu verschiedenen Zeiten das Ziel passieren.
a) Nenne die verschiedenen Einlaufreihenfolgen. Wie viele sind es?
b) Gib die Ergebnismenge Ω1 an, wenn nur der 1. Sieger interessiert.
c) Gib die Ergebnismenge Ω2 an, wenn nur der 1. und 2. Sieger festgestellt werden
soll.
2. Die drei Triebwerke eines Flugzeugs werden getestet. Gib die Ergebnismenge an,
wenn interessiert,
a) wie viele
b) welche Triebwerke nicht einwandfrei laufen.
3. In einem Land gibt es vier politische Parteien. A, B, C und D. Welche der
Mengen sind mögliche Ergebnismengen zu der Umfrage: Welche Partei würden Sie
wählen, wenn morgen Wahltag wäre?
a) {A;B;C;D; keine} b) {A; B oder C; keine} c) {A;sonstige; keine} d) {A oder B}
Aufgaben
1. Bei einem Wettrennen starten die vier Personen A,B,C und D. Man geht davon
aus, dass alle Läufer zu verschiedenen Zeiten das Ziel passieren.
a) Nenne die verschiedenen Einlaufreihenfolgen. Wie viele sind es?
b) Gib die Ergebnismenge Ω1 an, wenn nur der 1. Sieger interessiert.
c) Gib die Ergebnismenge Ω2 an, wenn nur der 1. und 2. Sieger festgestellt werden
soll.
2. Die drei Triebwerke eines Flugzeugs werden getestet. Gib die Ergebnismenge an,
wenn interessiert,
a) wie viele
b) welche Triebwerke nicht einwandfrei laufen.
3. In einem Land gibt es vier politische Parteien. A, B, C und D. Welche der
Mengen sind mögliche Ergebnismengen zu der Umfrage: Welche Partei würden Sie
wählen, wenn morgen Wahltag wäre?
a) {A;B;C;D; keine} b) {A; B oder C; keine} c) {A;sonstige; keine} d) {A oder B}
Ereignis
Jede Teilmenge von Ω
heißt Ereignis.
Beispiel:
Einmaliges Würfeln
mit Ω = {1,2,3,4,5,6}
E: “gerade Augenzahl“
E = {2;4;6}
Besondere Ereignisse
●
Enthält ein Ereignis nur
ein Ergebnis, so nennt
Beispiel:
man es
E1={6}
„Elementareignis“
●
●
●
Ω heißt „sicheres
Ereignis“
●
Die leere Menge
so betrachte ich es als sicher,
dass eine der 6 Zahlen der
Menge gewürfelt wird.
{} oder ∅
heißt das „unmögliche
Ereignis“
Wähle ich Ω ={1,2,3,4,5,6}
●
Ich betrachte es als unmöglich,
keine der 6 Zahlen zu würfeln.
Aufgaben
1. Zwei Freunde spielen das Knobelspiel
„Schere (S) , Stein (St), Papier (P)“
Notiere die Ergebnismenge Ω, das sichere und das unmögliche
Ereignis sowie die Ereignisse E1 und E2 mit E1:“Erster Spieler
gewinnt“, E2:“Keiner gewinnt“.
2. Gib die Mengen an, die folgende Ereignisse
beim zweimaligen Würfeln mit dem Tetraeder beschreiben:
E1: „Pasch“, E2:“Augensumme gerade“,
E3: „Erste Augenzahl kleiner als zweite“
Verknüpfung von Ereignissen
Ereignisse sind Mengen.
Verknüpfungen von Mengen:
Schnittmenge von A und B: A∩B
„A und B“
Vereinigungsmenge von A und B: A∪B „A oder B“
Komplementärmenge von A: A
„nicht A“
Stelle für das Würfeln mit einem Würfel die Schnittund Vereinigungsmenge von A:“Augenzahl prim“
und B:“Augenzahl höchstens 4“ dar. Nenne auch die
Komplementärmengen zu A und B.
Aufgabe
Auf Karins Schulweg gibt es drei Ampeln, die unabhängig voneinander
den Verkehr regeln. Katrin muss sie alle drei passieren.
a) Nenne die Ergebnismenge Ω für die Möglichkeiten der
Ampelschaltungen, falls nur Rot und Grün beachtet werden soll.
b) Gib die folgenden
Ereignisse an.
A: Alle Ampeln zeigen die
gleiche Farbe.
B: Die erste Ampel zeigt
Rot.
C: Die zweite Ampel zeigt
Rot.
D: Höchstens eine Ampel
zeigt Rot.
c) Notiere die folgenden Ereignisse und beschreibe sie verbal:
R = B∩C , S = B∪C , T = A∩C , U = D
, V = A∩C
Laplace-Experimente
a) Werft in Gruppenarbeit zwei Münzen mit den
Prägungen „Kopf“ und „Zahl“ und notiert die
relativen Häufigkeiten nach 200-maligem Werfen
für die Ereignisse E1:„beide Kopf“, E2:„beide Zahl“
und E3:„unterschiedliche Prägung“
Ereignisse
relative
Häufigkeit
h200(E)
E1
E2
E3
Laplace-Experimente
b) Einigen Schülern ist es zu langweilig, die Würfe durchzuführen. Sie
wollen lieber durch Berechnungen, den Ausfall des Zufallsexperiments
vorhersagen.
Sie schlagen folgende Modelle zur Beschreibung des Versuchs vor:
Ereignisse
Ω1 = {beide Kopf, beide Zahl,
unterschiedlich}
Ω2 = Ω1
Ω3 = {(K|K),(Z|Z),(Z|K),(K|Z)}
beide Kopf
Wahrscheinlichkeit
1
3
P(E)
beide Zahl
unterschiedlich
1
3
1
3
unterschiedlich
Ereignisse
beide Kopf
beide Zahl
Wahrscheinlichkeit
P(E)
1
4
1
4
Ereignisse
(K|K)
(Z|Z)
(Z|K)
(K|Z)
Wahrscheinlichkeit
111
444
1
4
1
4
1
4
P(E)
1
2
Aufgabe (Fortsetzung)
●
Vergleicht mit den relativen Häufigkeiten aus a)
und beschreibt, welche Modelle das
Zufallsexperiment tatsächlich widerspiegeln.
●
Welche Ergebnismenge ist zur Berechnung der
Wahrscheinlichkeiten am geeignetsten?
Begründet.
Laplace-Experiment
Ein Zufallsexperiment, dessen Ergebnisse als
gleichwahrscheinlich angenommen werden,
heißt Laplace-Experiment.