Прочитайте и переведите отрывок текста из учебника

Прочитайте и переведите отрывок текста из учебника Riessinger Mathematik fuer Ingenieure.
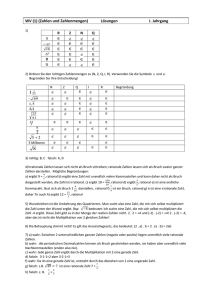
Выпишите незнакомые слова
Выполните упражнения
Перескажите текст
Rechnen mit Zahlen
Die einfachsten Zahlen, mit denen wohl jeder seine rechnerische Karriere
beginnt, sind mit Sicherheit die allseits bekannten natЁurlichen Zahlen. Der
Ordnung halber werde ich kurz aufschreiben, was man unter der Menge der
nat¨urlichen Zahlen versteht, und danach ein paar Worte zu dieser Definition
sagen.
1.1.1 Definition Unter der Menge der nat¨urlichen Zahlen versteht man
die Menge
IN = {1, 2, 3, ...}.
Besonders aufregend ist das nicht, aber deshalb heissen die Zahlen ja auch
”natЁurlich“. Was dabei genau mit dem Wort ”Menge“ gemeint ist und was
man mit Mengen anstellen kann, werden Sie im ersten Kapitel des Lehrbuchs
lernen. FЁur unsere Zwecke genЁugt es, dass man in einer Menge einige Dinge
zusammenfasst, die man gerne als eine grosse Einheit betrachten wЁurde.
In der Regel schreibt man so etwas dann genauso auf wie in der Definition
1.1.1: man schreibt die Elemente der Menge einfach zwischen zwei sogenannte
Mengenklammern { und }, und schon ist klar, wer zur Menge gehЁoren soll.
Dass man mit den natЁurlichen Zahlen nicht alle VorgЁange in der richtigen
Welt darstellen kann, merken Sie spЁatestens dann, wenn Sie ein Haus kaufen
und dafЁur einen Kredit brauchen. ЁUblicherweise geraten Sie damit tief in die
roten Zahlen, und die mathematische Beschreibung dieser roten Zahlen sind
die negativen Zahlen. FЁur gewЁohnlich bringt man sie in der grЁosseren Menge
der ganzen Zahlen unter, die aus den natЁurlichen Zahlen, den negativen Zahlen
und der Null besteht.
1.1.2 Definition Unter der Menge der ganzen Zahlen versteht man die
Menge
ZZ = {... − 3,−2,−1, 0, 1, 2, 3, ...}.
In der Menge der ganzen Zahlen sind auch die RechenmЁoglichkeiten nicht
so eingeschrЁankt wie bei den natЁurlichen Zahlen. In IN kann ich nЁamlich so
richtig sorglos nur addieren und multiplizieren, denn damit verlasse ich nicht
den Bereich der natЁurlichen Zahlen. Beim Subtrahieren wird es schon kritisch,
weil zum Beispiel die Rechnung 2−5 innerhalb der natЁurlichen Zahlen keinen
Sinn macht. Sie ist selbstverstЁandlich absolut problemlos, wenn man sich mit
den ganzen Zahlen anfreunden kann, denn es gilt 2−5 = −3. Hin und wieder
treten aber gerade beim Subtrahieren negativer Zahlen kleine Probleme auf,
und deshalb werfen wir einen kurzen Blick auf ein paar Beispiele.
1.1.3 Beispiele Solange man nur addiert, gibt es kaum Schwierigkeiten.
So ist zum Beispiel:
3 + (−2) = 3 −2 = 1, 17 + (−25) = 17 − 25 = −8.
Beim Subtrahieren muss man etwas aufpassen, da sich zwei Minuszeichen
gegenseitig aufheben und zu einem schlichten Plus werden. Deshalb gilt zum
Beispiel:
8 − (−17) = 8 + 17 = 25, −9 − (−12) = −9+ 12 = 3.
Bei der Muliplikation gibt es einen ganz Ёahnlichen Effekt, der auftritt, wenn
man zwei negative Zahlen miteinander multipliziert.Wegen der Regeln ”Minus
mal Minus = Plus“ und ”Minus mal Plus = Minus“ hat man zum Beispiel:
5 ・ (−6) = −30, (−5) ・ (−6) = 30.
Das Dividieren ganzer Zahlen schliesslich gehorcht in Bezug auf die Vorzeichen
im Wesentlichen den gleichen Gesetzen wie die Multiplikation, sofern man die
Zahlen Ёuberhaupt durcheinander teilen kann, ohne den Bereich der ganzen
Zahlen zu verlassen. Das heisst beispielsweise:
(−8) : 4 = −2, (−8) : (−4) = 2,
da sich im letzten Beispiel die beiden Minuszeichen gegeneinander aufheben.
Mit den ganzen Zahlen kommt man so lange zurecht, bis man auf Divisionsaufgaben
stЁosst. Sicher kann man 4 : 2 oder auch 51 : 3 rechnen, aber schon bei
4 : 3 gerЁat man etwas in Verlegenheit, weil die Division nicht mehr aufgeht. Um
also beim Dividieren allen Schwierigkeiten aus dem Weg zu gehen, brauchen
wir noch eine weitere Zahlenart, nЁamlich die Menge der rationalen Zahlen, in
der sich einfach nur alle BrЁuche versammeln.
1.1.4 Definition Unter der Menge der rationalen Zahlen IQ versteht man
die Menge aller BrЁuche der Form a
b,
wobei a und b ganze Zahlen sind und
ausserdem b nicht Null sein darf. Dabei heisst a der ZЁahler und b der Nenner
des Bruchs a
b.
Hier habe ich nun zum ersten Mal Platzhalter benutzt, sogenannte Variablen,
die die Stelle von Zahlen einnehmen. Das ist manchmal nicht zu vermeiden.
Im Fall der rationalen Zahlen ist es nicht so ganz einfach, alle rationalen
Zahlen so aufzulisten, wie ich das bei den natЁurlichen Zahlen und den ganzen
Zahlen gemacht habe. Besser ist es, man beschreibt die Menge dadurch,
dass man erklЁart, welche Zahlen zu ihr gehЁoren, und genau das habe ich mit
Hilfe der Variablen a und b getan. Typische Vertreter der Menge IQ sind also
beispielsweise 3
4 oder
5.
auch −2
Beachten Sie, dass damit im Grunde nur das
Ergebnis einer Division anders aufgeschrieben wird, denn 3
4 ist
nichts anderes
als 3 : 4, und bei −2
5 handelt
es sich nur um −2 : 5. Und deshalb darf der
Nenner eines Bruchs auch auf keinen Fall Null sein, weil man durch Null nicht
vernЁunftig dividieren kann.
WЁahrend die meisten Leute mit dem ganzzahligen Rechnen einigermassen
zurechtkommen, bereitet die Bruchrechnung oft schon etwas mehr Probleme.
Es gibt ein paar Regeln fЁur das Rechnen mit BrЁuchen, die man auch als Formeln
aufschreiben kann und die Sie sicher in der einen oder anderen Form
wЁahrend Ihrer Schulzeit gelernt haben. Ich mЁochte hier allerdings darauf verzichten,
die Regeln formelmЁassig aufzuschreiben, sondern Ihnen an einigen
Beispielen zeigen, wie man mit BrЁuchen rechnet und dabei die passenden Regeln
in verbaler Form erklЁaren.
1.1.5 Beispiele
(i) Am einfachsten ist das Multiplizieren von BrЁuchen. Man multipliziert zwei
BrЁuche, indem man ZЁahler mit ZЁahler und Nenner mit Nenner multipliziert.
Das heisst zum Beispiel:
2/3 ・5/7=2 ・ 53 ・ 7=10/21.
(ii) Hat man einmal die Multiplikation von BrЁuchen zur VerfЁugung, dann ist
es ganz leicht einzusehen, dass man einen Bruch auf beliebig viele verschiedene
Arten schreiben kann. Hat man zum Beispiel den Bruch 3
2,
so gilt
natЁurlich
3
2
=
3
2 ・1 =
3
2・
5
5
=
15
10.
Also sehen die BrЁuche 3
2 und 15
10 zwar
unterschiedlich aus, bedeuten aber
genau dasselbe, weil ich 15
10 erhalten
2 auf
habe, indem ich 3
eine ganz bestimmte
Weise mit 1 multipizierte. Diese Methode, das Aussehen eines
Bruchs zu Ёandern, ohne etwas mit seinem Wert anzustellen, nennt man
erweitern. Sie funktioniert so, dass man ZЁahler und Nenner des Bruchs
mit derselben Zahl multipliziert. So ist zum Beispiel:
4
7
=
4・ 2
7・ 2
=
8
14,
aber auch
4
7
=
4 ・ 17
7 ・ 17
=
68
119.
Der umgekehrte Vorgang heisst k¨urzen. Dabei pflegt man ZЁahler und Nenner
durch die gleiche Zahl zu teilen, ohne etwas am Wert des Bruchs zu
Ёandern. Im letzten Beispiel heisst das:
68
119
=
4 ・ 17
7 ・ 17
=
4
7,
denn ich konnte ZЁahler und Nenner durch 17 teilen.
(iii)Das Dividieren von BrЁuchen ist Ёahnlich einfach wie das Multiplizieren.
WЁahrend man beim schlichten Multiplizieren genau ZЁahler mit ZЁahler und
Nenner mit Nenner malnimmt, muss man zum Dividieren den sogenannten
Divisor umdrehen und dann anschliessend beide BrЁuche miteinander
multiplizieren. KЁurzer gesagt: man dividiert einen Bruch durch einen zweiten
Bruch, indem man den ersten Bruch mit dem Kehrwert des zweiten
Bruchs multipliziert. Somit ist:
3
2
:
7
4
=
3
2・
4
7
=
3・ 4
2・ 7
=
3・ 2
7
=
6
7,
wobei ich unterwegs ausgenutzt habe, dass man den entstehenden Bruch
durch 2 kЁurzen konnte.
(iv)Am schwierigsten von allen Operationen ist die Addition bzw. Subtraktion
von BrЁuchen. Man kann leider nicht einfach ZЁahler auf ZЁahler und Nenner
auf Nenner addieren. Wenn Sie sich beispielsweise einen halben Kuchen
und einen viertel Kuchen vorstellen, dann haben Sie nach dem Verzehr
beider Teile vermutlich Magenschmerzen, aber ganz sicher haben Sie drei
Viertel dieses Kuchens gegessen. In Zahlen heisst das:
1
2
+
1
4
=
3
4.
Offenbar kЁamen Sie zu einem vЁollig anderen Ergebnis, wenn Sie jeweils
ZЁahler und Nenner addieren wЁurden. Man muss also etwas raffinierter
vorgehen, und der SchlЁussel zur Bruchaddition ist der Begriff des Hauptnenners.
Sie kЁonnen die eben aufgestellte Kuchengleichung nЁamlich ganz
leicht einsehen, wenn Sie sich daran erinnern, dass 1
2= 2
4 gilt,
und rechnen:
1.1 Rechnen mit Zahlen 5
1
2
+
1
4
=
2
4
+
1
4
=
3
4.
Man muss also durch Erweitern oder KЁurzen dafЁur sorgen, dass beide
BrЁuche den gleichen Nenner haben, und dann kann man ganz simpel die
ZЁahler addieren. Das ist natЁurlich leicht in so einem Fall wie eben oder im
folgenden Beispiel:
7
3−
2
9
=
21
9−
2
9
=
19
9.
Etwas genauer muss man hinsehen, wenn man zwei Nenner hat, die nicht
sehr viel miteinander zu tun haben, wie zum Beispiel:
5
6
+
7
8.
Hier muss man erst einmal den passenden Hauptnenner finden, der offenbar
weder 6 noch 8 heisst. Man behilft sich damit, dass man das sogenannte
kleinste gemeinsame Vielfache sucht. Zum Beispiel ist 48 ein gemeinsames
Vielfaches von 6 und 8, da es Vielfaches von 6 und von 8 ist. Es ist aber
nicht das kleinste gemeinsame Vielfache, denn auch 24 ist ein gemeinsames
Vielfaches von 6 und 8, aber natЁurlich ist 24 kleiner als 48. In diesem Fall
nehme ich als Hauptnenner also die 24. Damit muss ich den ersten Bruch
mit 4 erweitern, den zweiten Bruch mit 3 erweitern und erhalte:
5
6
+
7
8
=
20
24
+
21
24
=
41
24.
So funktioniert das immer, egal ob Sie BrЁuche addieren oder subtrahieren
wollen. Zum Beispiel ist
7
10 −
3
4
=
14
20 −
15
20
=−
1
20.
Das kleinste gemeinsame Vielfache von 4 und 10 ist 20, und deshalb musste
ich den ersten Bruch mit 2 und den zweiten Bruch mit 5 erweitern.
So viel zur Bruchrechnung. Obwohl sie nicht besonders schwierig ist, haben
viele Leute eine recht groЯe Scheu davor und versuchen, sie zu vermeiden.
In gewissen Grenzen kann man das auch, wenn man bedenkt, dass eine
Bruch eigentlich nur eine Division ganzer Zahlen beschreibt, die man natЁurlich
auch einfach durchfЁuhren kЁonnte. Man muss dann nur damit leben, dass man
meistens Kommazahlen erhЁalt, die unter UmstЁanden nicht einmal nach einer
endlichen Anzahl von Stellen aufhЁoren. Sicher ist 1
2=
0, 5 und man hat eine
Zahl mit nur einer Stelle nach dem Komma. Aber wie Sie wahscheinlich
wissen oder einfach durch Dividieren ausrechnen kЁonnen, ist 1
3=
0, 33333...
und man hat eine Zahl mit unendlich vielen Stellen nach dem Komma. Dabei
ist es nur ein schwacher Trost, dass immer nur die 3 vorkommt, denn
auch unendlich viele Dreien kann kein Mensch hinschreiben. Wollen Sie also
1 Erste Rechenmethoden
mit solchen Dezimalzahlen rechnen, so mЁussen Sie unter UmstЁanden in Kauf
nehmen, dass Sie Rundungsfehler machen, weil Sie beim praktischen Rechnen
natЁurlich nach einer gewissen Anzahl von Nachkommastellen aufhЁoren
mЁussen. Das Ёandert aber natЁurlich nichts daran, dass man jeden Bruch auch
als Dezimalzahl schreiben kann, wobei die Dezimalzahl unter UmstЁanden unendlich
viele Stellen nach dem Komma hat.
Ich bin ziemlich sicher, dass ich Ihnen in diesem Abschnitt nichts nennenswert
Neues erzЁahlen konnte, aber es schadet nichts, sich auch die einfachen
Dinge noch einmal vor Augen zu fЁuhren. Im nЁachsten Abschnitt werde ich
Ihnen die AnfЁange des Rechnens mit Formeln zeigen.
¨Ubungen
1.1 Berechnen Sie:
(a) 6
35 ・ 7
3;
(b) 9
4: 6
5;
(c) −3
8・
453
10
.
1.2 Berechnen Sie:
(a) 7
6− 5
8;
(b) 13
20 + 54
15 ;
(c) 3
4−
10 _
.
_−
.
1