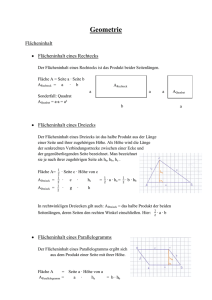
Aufgaben zur Geometrie

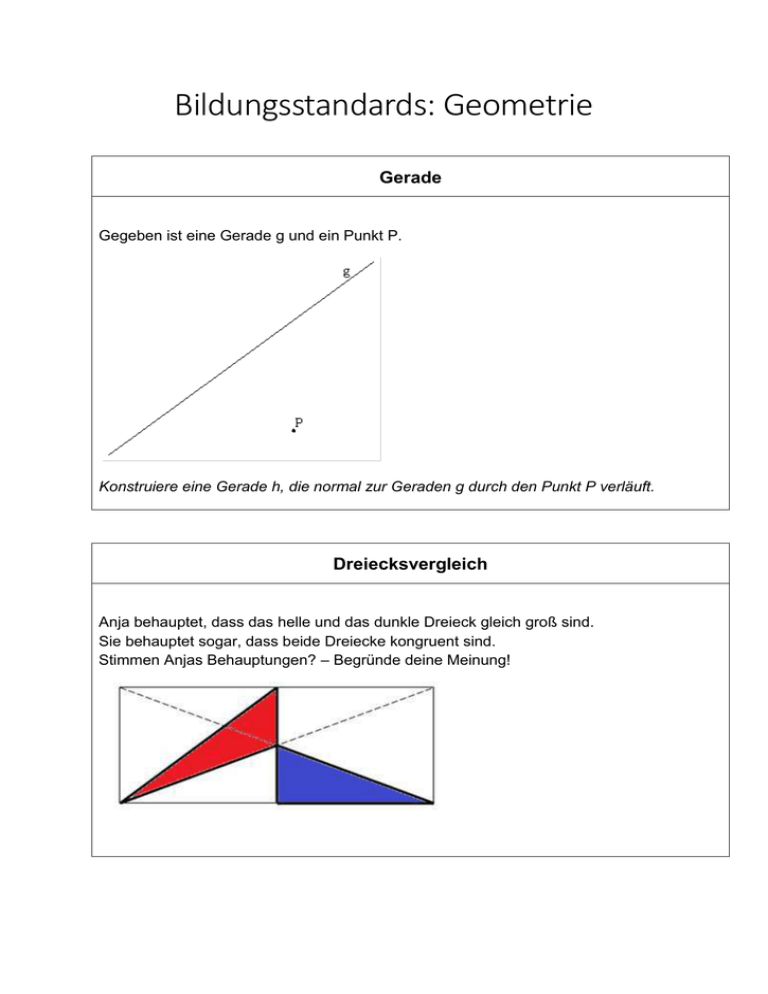
Bildungsstandards: Geometrie
Gerade
Gegeben ist eine Gerade g und ein Punkt P.
Konstruiere eine Gerade h, die normal zur Geraden g durch den Punkt P verläuft.
Dreiecksvergleich
Anja behauptet, dass das helle und das dunkle Dreieck gleich groß sind.
Sie behauptet sogar, dass beide Dreiecke kongruent sind.
Stimmen Anjas Behauptungen? – Begründe deine Meinung!
Streckensymmetrale
Gegeben ist die Strecke AB. Ermittle die Koordinaten jenes Punkts P auf der
Streckensymmetrale von AB, der als x-Koordinate +2 hat.
Figur
Ermittle den Flächeninhalt der dargestellten Figur.
Bilderrahmen - Verkehrszeichen
a) Das Bild (samt Rahmen) an der Wand ist ein Rechteck.
Das Bild im Inneren des überall gleich breiten Rahmens
ist ebenso ein Rechteck.
Sind diese beiden Rechtecke zueinander
geometrisch ähnlich?
Begründe deine Aussage!
b) Das Verkehrszeichen „Achtung, Fußgängerübergang!“
hat die Form eines gleichseitigen Dreiecks mit einem
überall gleich breiten roten Rahmen.
Sind das äußere und innere Dreieck
des Rahmens zueinander geometrisch ähnlich?
Begründe deine Aussage!
Gärtner
Ein Gärtner spannt eine Knotenschnur (die Abstände
zwischen zwei benachbarten Knoten sind immer gleich groß)
so wie in der Skizze dargestellt.
Er sagt: “Nun habe ich für das Blumenbeet einen rechten
Winkel festgelegt!“
Wieso kann er das mit Recht behaupten und wo liegt der
rechte Winkel?
Argumentieren 1.Kl. Fläche
Wie ändert sich der Flächeninhalt eines
Rechtecks, wenn man
a) die Länge verdoppelt
b) die Breite verdoppelt
c) die Länge und die Breite verdoppelt?
Erkläre dein Ergebnis deinem
Sitznachbarn/deiner Sitznachbarin.
Brennholz
Im Holzhandel ist es üblich, das Holz nach dem Volumen
abzurechnen.
Dabei werden verschiedene Einheiten verwendet.
1 fm (= 1 Festmeter) entspricht 1 m³ fester Holzmasse, d.h.
ohne Zwischenräume in der Schichtung.
1 rm (= 1 Raummeter) entspricht jener Menge gespaltenem
Holz in Form von gestapelten Holzscheiten, die das Volumen
von 1 m³ ausfüllt.
Zum Abschätzen des Raumbedarfes von ofenfertigem,
gespaltenem Brennholz kann angenommen werden, dass für
1 fm ungefähr
1,5 m³ Raum benötigt werden.
Zur Berechnung des Volumens eines Stammes wird der
„mittlere Durchmesser“ (= Durchmesser in der Mitte der
Gesamtlänge des Stammes) gemessen.
Ein Holzfäller hat für einen Kunden die neben stehende Liste
über gelieferte Baustämme erstellt.
a) Wie viel Festmeter Holz hat der Holzfäller seiner Kundschaft geliefert?
b) Wie viel € muss der Käufer bezahlen, wenn der Holzfäller für einen Festmeter
48 € inklusive Zustellung verlangt?
c) Wie groß ist der Raumbedarf für das gelieferte Holz, wenn es als gestapelte Scheite eingelagert
werden soll?
d) Die Kundschaft lager das Holz in einem Kellerabteil mit den Maßen
2 m x 2 m x 2,2 m ein.
Wie viel Festmeter könnte der Kunde noch nachkaufen, um das Kellerabteil ganz aufzufüllen?
e) Löse die Aufgaben a) bis c) auch mit Hilfe einer Tabellenkalkulation (z. B. EXCEL)!
Frau Bauer
Frau Bauer sagt zu ihrem Mann:
“Unser rechteckiger Gemüsegarten ist mir zu klein. Der Garten sollte eine doppelt so
große Anbaufläche haben.“
Herr Bauer antwortet:
„Wir haben genug Platz. Wir machen einfach jede Seite doppelt so lang. Und weil ich
deinen Wunsch kenne, habe ich auch schon eine neue, im Vergleich zur jetzigen doppelt
so lange Beeteinfassung gekauft.“
Schreib auf, was Frau Bauer ihrem Mann antworten wird, wenn sie sich die Antwort
genauer überlegt hat.
Netz eines Würfelecks
Otto will das Netz einer dreiseitigen Pyramide konstruieren, die genau in eine Würfelecke passt
(siehe Schrägriss). Er überlegt sich, wie ein passendes Netz aussehen könnte. Welches Netz soll er
ausschneiden und falten, damit die Pyramide in die Würfelecke passt? Kreuze die richtigen
Begründungen an.




Die grauen Seitenflächen müssen gleich groß sein.
Die weiße Dreiecksfläche muss ein gleichseitiges Dreieck sein.
Die weiße Dreiecksfläche muss ein rechtwinkeliges Dreieck sein.
Die grauen Seitenflächen müssen gleich groß wie in der Schrägrisszeichnung sein.
Deshalb ist folgendes Netz richtig:  A
B
C
Terme deuten im Kontext geometrische Figuren und Körper
Alle folgenden Terme können als Flächen- oder Volumensformeln gedeutet werden
(A … Flächeninhalt, V … Volumen; Kleinbuchstaben stehen für Längen, Großbuchstaben für Flächen
oder Volumina).
a)
Entscheide in jeder Zeile, ob die Deutung des Terms richtig oder falsch ist.
Term
Flächenhalt der Figur oder
Bedeutung der Variablen
richtig
falsch
Volumen des Körpers
A
a·b
2
A eines rechtwinkligen Dreiecks
a, b … Katheten
B
a·b
2
A eines Deltoids
a, b … Diagonalen
C
a·b
2
A eines Rechtecks
a, b … Länge und Breite
D
a·b
2
A eines Parallelogramms
a·b
2
A eines Dreiecks
E
b)
a … Seitenlänge
b … Höhe auf die Seite a
a … Basis (Grundlinie)
b … Höhe auf a
Schreibe jeweils auf, für welche Figuren bzw. Körper durch den Term der Flächeninhalt bzw. das
Volumen berechnet werden können.
Beschreibe, wofür die Variablen in deiner Deutung stehen.
Term
Flächenhalt der Figur oder
Volumen des Körpers
r·s
x·y·z
k·l·m
3
(x + y) · z
2
Bedeutung der Variablen
x·x·y
3
t·t·t
G·y
3
Regentonne
Eine zylinderförmige Regentonne ist 82 cm hoch und hat einen Durchmesser
von 82 cm. Sie ist zur Hälfte mit Regenwasser gefüllt.
Was wird durch die Rechnung
82 2
( 2 ) ∙ 𝜋 ermittelt?
Kreuze die richtige Antwort an.
O Das Volumen der Regentonne
O Die Oberfläche der Regentonne
O Das Volumen des Regenwassers
O Die Mantelfläche der Regentonne
O Die Grundfläche der Regentonne
O Der Umfang der Grundfläche der Regentonne
Gleiche Entfernung von zwei Seiten
Kennzeichne alle Punkte der markierten Fläche, die von den Seiten a und b gleich weit
entfernt sind.
Gleiche Entfernung von zwei Punkten
Kennzeichne alle Punkte der markierten Fläche, die von den Eckpunkten A und B gleich
weit entfernt sind.
Pythagoras H2, B
Berechne den Flächeninhalt A des Quadrats über der kürzeren Kathete.
Gasspeicher
Der Innenraum des abgebildeten
Gasspeichers
reicht nicht unter die Erdoberfläche.
Ermittle die ungefähre Höhe und den
ungefähren Durchmesser des
Behälters.
Hubschrauber
Der Rotordurchmesser eines Hubschraubers (d. h. die beiden gegenüberliegenden
Rotorblätter zusammen) beträgt 10,4 m.
Im Flug vollführen die Rotorblätter in jeder Sekunde
6 Umdrehungen.
Welche Geschwindigkeit erreichen die Spitzen der
Rotorblätter?
Gib die Geschwindigkeit auch in km/h an!
Pythagoras H3
Goldwürfel
Schon vor Tausenden von Jahren war das gelb glänzende
Edelmetall in Gebrauch und bis heute haben goldene Münzen,
Schmuck und Goldbarren ihre Anziehungskraft nicht verloren.
Bisher wurden insgesamt etwa 155 000 t Gold aus der Erde
geschürft.
Stell dir vor, du könntest daraus einen einzigen Würfel formen.
a) Schätze dessen Kantenlänge.
b) Berechne die Kantenlänge des Würfels und vergleiche mit deinem Schätzwert.
Die Dichte von Gold beträgt 19,3 kg/dm³.
Zahnpasta-Tube
a) Die beiden ungeöffneten Zahnpasta-Tuben wurden gemeinsam fotografiert.
Schätze die Inhalte der beiden Tuben in Millilitern.
b) Wo ist mehr drinnen?
Folgende Größen sind bekannt:
Linke Tube: Durchmesser 2,8 cm, Länge: 18 cm.
Rechte Tube: Durchmesser 3,2 cm, Länge: 15 cm.
1.
Welche einfachen geometrischen Körper können dir als Modell
für die Zahnpasta-Tuben dienen?
2.
Ermittle mit Hilfe deines Modells die
Volumina der beiden Tuben.
Welche Zahnpastainhalte ergeben sich, wenn man
davon ausgehen muss, dass auch
originalverschlossene Tauben aus technischen
Gründen immer 5 bis 10 cm³ Luft enthalten müssen.
3.
Wie oft kann man sich mit dem Inhalt der
linken Zahnpastatube die Zähne putzen? Triff
geeignete Annahmen und berechne.
Bildquelle: fotolia, toothbrushes and tube of toothpaste, Datei:
#82181080 | Urheber: rommma