Klänge hören und lesen - Uni Regensburg/Physik

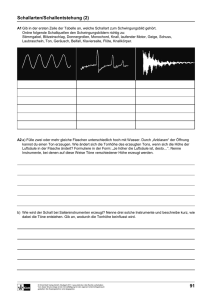
Klänge hören und lesen
von Karsten Rincke
Manuskript zum Beitrag Klänge hören und lesen. In Naturwissenschaften im Unterricht Physik, Heft 114, S. 10-13
Das Sonagramm
Farben und Bilder
In Abbildung 1 ist ein Beispiel für ein Diagramm zu sehen, das mit dem freien Programm Sonogram erzeugt wurde. In der
Horizontalen ist die Zeit aufgetragen, in
der Vertikalen die Frequenz (die Zahlenwerte sind im gezeigten Beispiel nur sehr
klein zu sehen). Dieses Sonagramm zeigt keine Momentaufnahme, sondern repräsentiert
einen gewissen Zeitraum eines akustischen
Signals. Neben den beiden Dimensionen Zeit
und Frequenz ist eine dritte Dimension im
Diagramm enthalten, die durch Farben kodiert ist, es ist die Amplitude einer bestimmten Frequenz. In Abbildung 1 sind hellere
und dunklere Bereiche zu sehen: Die helleren
Bereiche gehören zu Klangkomponenten einer bestimmten Frequenz mit relativ großer
Amplitude, die dunkleren Bereiche entsprechend zu leiseren Komponenten. Das Diagramm liefert ein Klangspektrogramm, ein
recht umfassendes Bild eines Klangs im Zeitverlauf.
Wenn man eine Stimmgabel anschlägt, ein
Instrument spielt oder einen Ton singt –
stets ist es nicht nur ein Ton in einer bestimmten Grundfrequenz, den wir hören,
sondern immer eine Sammlung von Tönen
mit unterschiedlichen Frequenzen, die bestimmte Zahlenverhältnisse zu einander einhalten. Die Obertöne, die Vielfachen der
Grundfrequenz, können bei ein und demselben Grundton mit unterschiedlichen Amplituden auftreten. In dieser Vielfalt der möglichen Amplituden liegt die Vielfalt der Klangfarben verborgen. Jeder Ton – der Genauigkeit halber müssten wir sagen Klang, der
auf einem Instrument gespielt oder der gesungen wird, hat sein eigenes Spektrum an
Obertönen zum Grundton. Um die Farbigkeit der Klänge zu beschreiben, bietet unsere Sprache Attribute wie »dumpf, brillant,
hell, dunkel, kehlig, voll« und viele weitere
Wörter an. Neben den sprachlichen Repräsentationen sind bildliche Darstellungen gebräuchlich. In diesem Beitrag wird das Sonogram vorgestellt, das sich vielfältig einsetzen lässt und zudem eine überraschend klare Verbindung zur klassischen Notation von
Klängen zeigt, dem uns bekannten Musiknotensatz.
Wenn wir einen Klang wahrnehmen und entscheiden, aus welcher Quelle er stammen
könnte, dann wertet unser Gehör überraschenderweise aber nicht allein die Farbigkeit des Klangs aus. Im letzten Abschnitt dieses Beitrags wird gezeigt, dass auch das Einschwingen eines Instruments eminente Bedeutung für die richtige Zuordnung eines
Klangs hat.
Die ähnlichen Begriffe des Sonagramms und
des Sonogramms werden nicht immer klar
auseinander gehalten: Der Begriff des Sonogramms wird eher für Diagramme verwendet, die die räumliche Verteilung eines (Ultra)schallechos verwenden, um auf
die räumliche Struktur des Gegenstands zu
schließen, der das Echo zurück wirft. Frequenz und Zeitverlauf sind dann unwichtig.
Sonogramme finden in der Medizin Einsatz,
bekannt sind zum Beispiel die Sonogramme,
die einen Embryo im Mutterleib zeigen. Ihren Ursprung haben sie in der Technik zur
Ortung von Unterseebooten. Der Begriff des
Sonagramms wird dagegen eher für Diagramme verwendet, die die Struktur eines
1
Klangs zeigen (im Hinblick auf die enthaltenen Frequenzen), nicht die eines Körpers,
der ein Echo erzeugt. Dass die Macher des
in diesem Beitrag verwendeten Programms
den Namen Sonogram für ihr Produkt gewählt haben, und nicht Sonagramm, wie eigentlich zu erwarten wäre, zeigt, dass diese Unterscheidungen offenbar nicht ganz so
trennscharf eingehalten werden. In der Tat
haben beide Darstellungsarten eine wichtige Gemeinsamkeit, und zwar den Zweck betreffend, zu dem sie vorherrschend eingesetzt werden: Sie stellen bildgebende Verfahren dar, die für Diagnosezwecke eingesetzt
werden, so etwa das Sonagramm in der logopädischen Diagnostik oder in der Biologie,
wenn es um die Identifikation von Tierlauten
geht.
Wenn man Klänge darstellen möchte, bietet sich eine Reihe von Möglichkeiten mit je
eigenen Stärken an: Der klassische Notensatz arbeitet mit den Bestimmungsstücken
Zeit und Tonhöhe: Eine zeitliche Grundmetrik wird vorgegeben (z. B. »adagio«), und
die zeitliche Länge einer jeden Note wird relativ zu dieser Grundmetrik notiert (ganze
Noten, Achtelnoten u.s.w.). Damit liegt die
zeitliche Struktur der Klangfolge fest. Die
Tonhöhe der Klänge wird entlang der zeitlichen Struktur als Höhe relativ zu einem System aus fünf Notenlinien und vier Zwischenräumen angegeben. Das Notensystem stellt –
phhysikalisch ausgedrückt – ein System zur
Darstellung der Frequenz in Abhängigkeit
von der Zeit dar. Zusätzliche Vorgaben wie
forte oder piano sagen etwas über die Lautstärke, physikalisch also Amplitude der Töne.
Eine andere Form der Darstellung ist die, die
man beispielsweise erhält, wenn man einen
Klang mit dem Programm Audacity1 erzeugt
oder verarbeitet: Hier wird der Verlauf der
Amplitude in Abhängigkeit von der Zeit aufgetragen, diese Darstellungart heißt Oszillogramm und ist auch in Abbildung 1 (links)
ganz unten angedeutet. Die beiden Darstellungsformen sind ohne Einschränkung für
ein und dieselbe Klangfolge geeignet, betonen aber je unterschiedliche Aspekte.
Das Sonagramm ähnelt in der Art der Darstellung dem Notensatz, enthält jedoch eine
Reihe weiterer Aspekte, die es für den Unterricht interessant machen: Es ermöglicht, die
Unterschiede in den Klangfarben, die wir mit
den oben angedeuteten sprachlichen Mitteln
abbilden können, auch im Bild zu repräsentieren. Für die Beispiele in diesem Beitrag
wurde das Programm Sonogram 2 von Christoph Lauer verwendet. Abbildung 1 zeigt
ein Beispiel. Es wurde aus dem Anfang des
Wenn man das Sonagramm als Darstellungsform in den Unterricht einbeziehen möchte,
bieten sich folgende methodische und inhaltliche Schwerpunkte an:
• Das Sonagramm ist eine Repräsentationsform für Klänge, die mit anderen Formen konkurriert. Der bewusste Wechsel der Darstellungsform fordert heraus und hilft, fachliche und ästhetische Aspekte zum Gegenstand der
Auseinandersetzung zu machen.
• Das Sonagramm ähnelt dem Musiknotensatz. Schülerinnen und Schüler, die
mit dem Notensatz vertraut sind oder
sogar ein Instrument spielen, können
hier in besonderer Weise mit selbst anzufertigenden Tonaufnahmen einbezogen werden.
• Die Verbindung zum Musiknotensatz
schafft Anknüpfungspunkte für einen
fächerverbindenden Unterricht.
1 Frei
erhältlich unter http://audacity.sourceforge.net/?lang=de.
für alle gängigen Architekturen erhältlich unter http://sourceforge.net/projects/sonogram/
3 Ursprünglich von Lori Liebermann, bekannt aber erst seit der Veröffentlichung durch Roberta Flack (1970er)
und der Fugees (1990er).
2 Frei
2
Songs Killing me softly 3 gewonnen, dessen schließend mit dem Programm Sonogram
Melodie mit einer einzelnen Gitarre aufge- geöffnet. Rechts neben dem Sonagram sind
nommen wurde. Die Audiodatei wurde an- die Noten des Liedanfangs gezeigt.
Wenn ein Klang wie hier mit einer Gitarre erzeugt und mit Hilfe eines Computers aufgezeichnet wird, dann wird er digitalisiert. Die Verarbeitung digitaler Tonsignale basiert auf
einem erheblichen mathematischen Aufwand, der hier nicht behandelt wird (für Interessierte sei auf das gut verständliche Buch von (Azizi, 1990) verwiesen). Eine grundsätzliche
Kenntnis ist jedoch nötig, wenn man die bildlichen Darstellungen im eigenen didaktischen
Interesse steuern möchte: Wenn der Computer die Spannungswerte eines Mikrofons misst
und speichert, dann tut er dies in einer Folge von diskreten Zeitpunkten. Alles, was zwischen diesen Zeitpunkten mit der Spannung passiert, wird ignoriert. Auch wenn die zu
diskreten Zeitpunkten gespeicherten Messwerte sehr genau eingelesen werden (große Anzahl von Bits), entsteht die Frage, ob die »verpassten Messwerte« zwischen den Messzeitpunkten in der gespeicherten Zahlenfolge vollständig repräsentiert sind oder nicht. Man
möchte annehmen, dass der Computer von diesen »verpassten Messwerten« nichts wissen
kann. Das würde jedoch bedeuten, dass wir das digitale Ergebnis des Einlesevorgangs mit
Misstrauen betrachten müssten. Die Frage, wann ein digitales Signal sein analoges Vorbild
perfekt repräsentiert oder nur eingeschränkt, wird durch das so genannte Shannonschen
Abtasttheorem geklärt. Dieses Theorem stellt einen Zusammenhang zwischen der Abtastfrequenz und dem Frequenzspektrum des digitalen Signals her. Die Abtastfrequenz bezeichnet die Anzahl der Datenpunkte, die pro Sekunde von einem analogen Signal durch
den Computer genommen werden. Das Theorem sagt, dass diese Abtastfrequenz mindestens doppelt so hoch sein muss wie die höchste Frequenz, die im Obertonspektrum eines
Klangs vorkommt. Wenn diese Bedingung erfüllt ist, dann können alle vermeintlich verpassten »Messwerte« korrekt rekonstruiert werden. Man darf dann dem digitalen Ergebnis
des Einlesevorgangs als Abbild seines analogen Vorbilds trauen. Ist die Abtastfrequenz zu
niedrig, dann können nicht alle verpassten Messwerte rekonstruiert werden. Dieser Mangel schlägt sich dann darin nieder, dass das Obertonspektrum des Klangs beim Einlesen
zu einem Teil verloren geht.
Audio-CDs werden beispielsweise mit einer Abtastfrequenz von 44, 1 kHz hergestellt. Das
bedeutet, dass im digitalen Signal Frequenzen bis zu 22, 05 kHz repräsentiert sein können
– ein Wert, den wir mit unserem Gehör bereits nicht mehr wahrnehmen können. Würden
CDs nur mit einer Abtastfrequenz von 2000 Hz hergestellt, dann würde die Musik nach
der Digital-Analog-Rückwandlung keine höheren Frequenzen als 1000 Hz enthalten – die
»verpassten Messwerte« beim Einlesen und Digitalisieren würden dafür sorgen, dass das
Endergebnis sehr vom analogen Vorbild abwiche. Es fehlten alle Obertöne jenseits von
1000 Hz und die Musik hörte sich an wie auf einem Mittelwellensender.
Kasten 1: Fachinformation zur Digitalisierung von Audiodaten
3
Wenn eine wav-Datei mit dem Programm Sonogram geöffnet wird, dann bestimmt das
Programm, mit welcher Abtastfrequenz die Datei erzeugt wurde. Wenn sie mit Audacity aufgenommen wurde, dann wird diese Frequenz bei 44, 1 kHz liegen. Sonogram erzeugt dann ein Bild, dessen Frequenzbereich (vertikal) von 0 bis 22, 05kHz reicht. Da sich
die Grundtöne, die wir mit einem Instrument spielen, aber im Bereich weniger Hundert
Hertz befinden, schrumpft die Darstellung relevanter Daten auf den unteren Bereich des
Bildes zusammen. Diesem Umstand begegnet man, indem man in Audacity eine entsprechend niedrigere Abtastfrequenz einstellt (Bearbeiten - Einstellungen - Qualität - Samplefrequenz). Für das Bild in Abbildung 1 wurden 8000 Hz gewählt. Dann wurde eine Aufnahme gestartet und anschließend als *.wav exportiert. Das Resultat wird anschließend
mit dem Programm Sonogram geöffnet.
Kasten 2: Praktische Hinweise zu Audacity und Sonogram
Sonagramme erstellen und
verwenden
gangspunkt für eine interessante Demonstration gewählt werden kann.
Das hier vorgestellte Programm ist in Java
programmiert und sollte auf allen Systemen
verwendet werden können. Seine Möglichkeiten gehen weit über das hinaus, was für
den Unterricht sinnvoll ist. Wenn es geeignet
eingesetzt werden will, sind einige grundsätzliche Informationen über die Verarbeitung digitaler Signale wichtig, die in Kasten 1 erläutert werden. In Kasten 2 wird erklärt, auf welche Einstellungen in Audacity bei Audioaufnahmen zu achten ist, damit
das Resultat in Sonogram sinnvoll verwendet werden kann.
Für den Einsatz im Unterricht bieten sich
u.a. die oben aufgezählten Schwerpunkte an.
Der Aspekt »Klangfarbe« kann dabei einen
inhaltlichen Schwerpunkt bilden. Es ist dabei auch reizvoll, die eigene Stimme zu untersuchen, insbesondere nachzusehen, wie
sich zum Beispiel die unterschiedliche Färbung der Vokale »O« und »I« im Bild niederschlägt. Es zeigt sich, dass das »I« über ein intensiveres Obertonspektrum verfügt. Wenn
man Instrumente vergleicht, mit denen man
je denselben Grundton anspielt, zeigt sich,
dass es in der Regel nicht leicht ist, die Spektren in den Bildern zu unterscheiden. Der
folgende Abschnitt geht dieser Beobachtung
genauer nach und zeigt, wie sie zum Aus-
Die Bedeutung des
Einschwingvorgangs
Wenn man mit einer Orgelpfeife, einer Oboe
oder einer Klarinette einen Ton anstimmt,
so muss sich dieser Ton erst im Verlauf der
ersten Bruchteile von Sekunden entwickeln.
Das System muss sich einschwingen. Die im
Basisartikel gezeigten Beispiele, mit denen
die Verhältnisse in einer Orgelpfeife nachgestellt werden, lassen diesen Einschwingvorgang sehr deutlich erkennen. Wenn die erste
Zone verdichteter Luft auf das Ende der Pfeife zu läuft, dann sind die Verhältnisse noch
genau so, wie sie auch außerhalb einer Pfeife wären. Man könnte sagen, dass die Zone verdichteter Luft noch nichts davon weiß,
dass sie in einem Rohr propapgiert. Das Modellexperiment zur Orgelpfeife im Beitrag
Aus dem Rauschen der volle Klang weist
ebenfalls darauf hin: Der Ton, der sich im
Rohr bildet, ist nicht sofort nach dem Einschalten des Modells vorhanden, sondern es
dauert einen Moment, bis er sich eingestellt
hat. Bei Musikinstrumenten ist dieser Zeitraum extrem kurz, andernfalls wäre es kaum
möglich, Sechzehntel Noten zu spielen. Dass
4
das Gehör in diesem Bruchteil einer Sekunde
Wesentliches über die beteiligten Instrumente registriert, dass es also die Charakteristik
des Einschwingvorgangs zur Detektion des
Klangs nutzt, zeigt das folgende Experiment,
das (Taylor, 1994, 92ff.) entnommen ist.
ten passend zuzuordnen, ist dasselbe im Fall
2b außerordentlich schwierig. Da alle Instrumente zur selben Zeit einsetzen, sind die
Anfänge schlecht unterscheidbar. Sie werden
vermeintlich unterscheidbarer, wenn Instrumente fortfallen. Dennoch fällt die richtige
Zuordnung schwer. Der Grund liegt darin,
dass der Hörer nicht mehr über die Information verfügt, wie er sie aus dem Einschwingvorgang wie im Fall 2a entnehmen konnte. Wenn sie einmal mit einem Ton eingesetzt haben, klingen viele Instrumente überraschend ähnlich. Wer sich den Einschwingvorgang der Saite einer Geige oder eines
Blasinstruments einmal in Zeitlupe anhören
möchte, mache eine entsprechende Aufnahme und verzögere das Abspielen zum Beispiel mit dem Programm Audacity. Im linken Teil des Fensters findet man einen Schieberegler, mit dem man unterschiedliche Abspielgeschwindigkeiten realisieren kann. Der
Ton ist dann entsprechend tief, aber man
kann sehr viel besser wahrnehmen, wie sich
das Instrument einschwingt. Ebenfalls kann
man mit dem Programm den Abschnitt eines Tons herausschneiden, während dessen
sich das Instrument einschwingt. Wenn man
eine kurze Melodie, die mit einem Klavier
gespielt wurde, Ton für Ton in dieser Weise
bearbeitet, klingen die Töne auf einmal sehr
ausdruckslos. Dies ist sicher ein Grund dafür, dass sich gute Pianistinnen und Pianisten auch darin auszeichnen, wie sie ihr Instrument anschlagen.
Vorbereitungen
1. Für dieses Experiment eigenen sich
reale Instrumente. Drei Schülerinnen
oder Schüler, die ein Instrument spielen, das einen dauerhaften Ton erzeugt
(Blas- oder Streichinstrumente), verbergen sich hinter einer Leinwand. Sie
werden angewiesen, alle den gleichen
Ton anzustimmen und auszuhalten.
2a. Die Schülerinnen und Schüler setzen
nicht alle gleichzeitig, sondern nacheinander mit ihrem Ton ein. Die Klasse,
die die Instrumentalisten nicht sehen,
wohl aber hören kann, erhält den Auftrag, sich zu notieren, in welcher Reihenfolge die Instrumente eingesetzt haben.
2b. Nun setzen die Schülerinnen und Schüler gleichzeitig mit ihrem Ton ein, sie
hören aber zeitlich versetzt gegeneinander auf. Zuletzt ist also nur noch ein
Instrument zu hören, bis auch dieses
verstummt. Die Klasse erhält den Auftrag, zu notieren, in welcher Reihenfolge die Instrumente den Ton beendet haben.
Literatur
Wahrnehmung und Deutung
Azizi, S. A. (1990). Entwurf und Realisierung
digitaler Filter. München: Oldenbourg.
Während es im Fall 2a in der Regel mög- Taylor, C. (1994). Der Ton macht die Physik.
lich ist, die gehörten Klänge den InstrumenBrauschweig, Wiesbaden: Vieweg.
5
Abbildung 1: Der Beginn des Songs »Killing me softly« in zwei Formen der Darstellung,
links im Sonagramm, rechts im Notensatz. Eine Gegenüberstellung dieser Art
kann im Unterricht zum Ausgangspunkt dafür genommen werden, zu erkennen, was das Sonagramm zeigt. Offenbar sind die Informationen aus dem Notensatz zu einem guten Teil links wiederauffindbar. Dennoch eignet sich die
linke Darstellung kaum, und anhand ihrer das Stück mit der Gitarre nachzuspielen. Dafür verrät sie Überraschendes: Wenn wir das g anzupfen, dann
hören wir noch deutlich mehr!
Das Signal ganz unten (bei 100 Hz) ist vermutlich eine Störung bei der Aufnahme – sehr wahrscheinlich eine Resonanz in den beteiligten Geräten.
6