Version — Die Version bestimmt sich nur durch die beiden Kreise

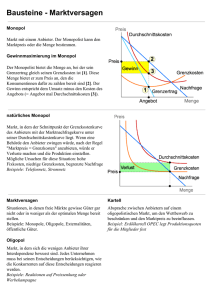
Version
—
Die Version bestimmt sich nur durch die beiden
Kreise ganz links. Lösungen für die anderen drei
Versionen finden Sie weiter hinten.
Betrachten Sie einen Markt, in dem die
Konsumenten bei einem Preis P < 30 genau Q = 10
Einheiten nachfragen. Bei P = 30 fragen die Konsumenten jede angebotene Menge zwischen 0 und
10 nach. Steigt der Preis über P = 30 wird nichts
nachgefragt.
Aufgabe:
• Was können Sie über die Preiselastizität der
Nachfrage auf dieser Nachfragekurve sagen?
(8 Punkte)
Die Nachfrage ist stets sehr elastisch
Die Nachfrageelastizität ist −1 bei P < 30
Die Nachfrage ist stets sehr unelastisch
Die Nachfrage ist unelastisch bei P < 30,
elastisch bei P = 30
1e: Die Nachfrage ist elastisch bei P < 30, unelastisch bei P = 30
1a:
1b:
1c:
1d:
P
30
(unelastisch)
Nachfrage
(elastisch)
MC
10
Q
• Ein Monopolist in diesem Markt hat keine Fixkosten und Grenzkosten M C = Q (Die Grenzkosten
nennen wir M C, die Menge Q). Bei welcher der
folgenden Mengen erzielt der Monopolist den
größten Gewinn?
(10 Punkte)
b 7.5
c
d
e
10
15
30
2: a 5
P
30
P
30
Nachfrage
→
Nachfrage
→
MC
MC
10
Q
10
Q
Der Gewinn des Monopolisten ist durch die
Fläche zwischen Preis und Grenzkostenkurve gegeben. Diese Fläche wird maximal bei Q = 10.
• Der Gewinn ist in diesem Fall etwa. . .
(10 Punkte)
b 200
c 250
d 300
e 150
3: a 0
Die obige Fläche bestimmt sich zu
30+(30−10)
2
· 10
• Die Konsumentenrente ist etwa. . . (12 Punkte)
b 250
c 300
d 150
e 200
4: a 0
Die Konsumentenrente ist die Fläche zwischen
Preis und Nachfragekurve — hier bleibt leider für
die Konsumenten nichts übrig.
• Nehmen Sie an, die Regierung könnte Preis und
Menge beliebig regulieren. Dadurch könnte die
Summe aus Produzentenrente und Konsumentenrente ungefähr um den folgenden Betrag gesteigert
werden. . .
(18 Punkte)
b 100
c
d
e
25
50
75
5: a 0
Die Summe aus Produzentenrente und Konsumentenrente ist die Fläche zwischen Nachfragekurve und Grenzkostenkurve. Die ist hier aber bereits ohne Regierungsintervention maximal.
• Nun betrachten Sie Mengenwettbewerb (Stackelberg) von zwei Anbietern. Erst produziert ein
Anbieter die Menge Q1 mit Grenzkosten von
M C = Q1 , dies beobachtet der zweite Anbieter
und produzert danach die Menge Q2 mit Grenzkosten M C = Q2 . Welche Menge wird der erste
Anbieter wählen?
(11 Punkte)
b 7.5
c
d
e
10
15
30
6: a 0
• Welche Menge wird der zweite Anbieter wählen?
(11 Punkte)
b
c
d
e 7.5
7: a 0
10
15
30
Der zweite Anbieter wird immer die Differenz
zwischen der Menge des ersten Anbieters und 10
produzieren. Gegeben dieses Verhalten ist es für
den ersten Anbieter optimal 10 zu wählen, der
zweite wird dann 0 wählen.
Für alle drei Produzenten ergibt sich der Gewinn
πi jeweils zu
π1
π2
π3
=
=
=
q1 · (30 − q1 − q2 − q3 )
q2 · (30 − q1 − q2 − q3 )
q3 · (24 − q1 − q2 − q3 )
damit ergeben sich die Ableitungen zu
dπ1 /dq1
dπ2 /dq2
dπ3 /dq3
=
=
=
30 − 2q1 − q2 − q3
30 − q1 − 2q2 − q3
24 − q1 − q2 − 2q3
Für jeden Produzenten im Markt muss die Ableitung Null sein. Daraus ergibt sich die Reaktionsfunktion
q1
q2
q3
=
=
=
(30 − q2 − q3 )/2
(30 − q1 − q3 )/2
(24 − q1 − q2 )/2
Diese Bedingungen sind erfüllt, wenn q1 = q2 = 9
und q3 = 3.
• B und C überlegen sich, ob es sich lohnt, in den
Markt einzutreten. Sie haben Markteintrittskosten KB bzw. KC . Betrachten Sie folgende Situation: Erst hat A die Möglichkeit, sich zu verpflichten, für den Fall des Markteintrittes von C die
Markteintrittskosten KC von C zu übernehmen.
Diese Entscheidung ist B und C bekannt. Danach
entscheiden sich B und C gleichzeitig, ob sie in den
Markt eintreten. Markieren Sie die notwendigen
Bedingungen, die gleichzeitig erfüllt sein müssen,
damit es ein Gleichgewicht gibt, in dem A die
Markteintrittskosten des C übernimmt (mehrere
Antworten möglich).
(50 Punkte)
9: aKB > 0 bKB < 144 cKB > 81 dKB < 81 eKB < 100
(50 Punkte)
10: aKC > 0 bKC > 9 cKC < 36 dKC > 36 eKC < 44
Die inverse Nachfrage nach Knorz sei
P = 31 − Q wobei P der Preis und Q die Menge
sind. Produzent A befindet sich allein im Markt und
hat Grenzkosten von 1. Es gibt zwei Konkurrenten,
B und C, die in den Markt eintreten können. Falls
sie das, einzeln oder alle beide, tun, stellen Sie das
gleiche Gut wie A her, und der Marktpreis bestimmt
sich durch Cournotwettbewerb. B hat Grenzkosten
von 1, C hat Grenzkosten von 7.
Wir bestimmen zunächst aus den obigen Reaktionsfunktionen Mengen für die möglichen Marktkonstellationen:
• Stellen Sie sich vor, B und C würden in den
Markt eintreten. Im Gleichgewicht gilt (mehrere
Antworten möglich):
(50 Punkte)
Daraus ergeben sich die Gewinne
Aufgabe:
8a:
8b:
8c:
8d:
8e:
A produziert mehr als 10 Einheiten
C produziert qC = 3
C produziert qC = 32
B produziert weniger als 10 Einheiten
A produziert genausoviel wie B
A, B, C
A, B
A, C
A
A, B, C
A, B
A, C
A
π1
81
100
144
225
q1
9
10
12
15
q2
9
10
0
0
π2
81 − KB
100 − KB
0
0
q3
3
0
6
0
π3
9 − KC
0
36 − KC
0
Nun können wir uns fragen, warum A die Kosten
des C übernehmen sollte. Irgendetwas muß sich für
ihn verbessern. Das ist aber nur der Fall, wenn wir
ohne Kostenübername in der Situation A, B sind. In
den drei anderen Situationen ist C entweder sowieso
schon im Markt, oder A bekommt bereits den maximal möglichen Gewinn. Wann aber sind wir in der
Situation A, B? Spieler B muß einen Anreiz haben,
einzutreten, d.h. 100−KB > 0. Spieler C muß einen
Anreiz haben, draußen zu bleiben, d.h. 9 − KC < 0.
Wenn nun A die Eintrittskosten des C übernimmt
sind die Gewinne
A, B, C
A, B
A, C
A
π1
81 − KC
100
144 − KC
225
π2
81 − KB
100 − KB
0
0
π3
9
0
36
0
Nun tritt C auf jeden Fall in den Markt ein. A verbessert sich aber nur, wenn B jetzt nicht mehr in
den Markt eintritt. Das macht B aber nur wenn
81 − KB < 0 Schließlich soll sich diese Aktion für A
auch lohnen, und das gibt uns die letzte Bedingung
144 − KC > 100.
Falls Sie in dieser Aufgabe neben den obigen Bedingungen auch redundante Bedingungen angegeben
haben (also z.B. KC > 9 und KC > 0), wird das
nicht als falsch bewertet.
Aufgabe:
Die Zwillinge Eva und Maria sind durstig und die einzigen Nachfragerinnen nach Himbeerbrause. Die Zahlungsbereitschaft von Eva sind 32
für das erste Glas, 20 für das zweite Glas, 15 für
das dritte Glas, und 0 für alle weiteren Gläser. Die
Zahlungsbereitsschaft von Maria sind 15 für das erste Glas, und 0 für alle weiteren Gläser. Nehmen
Sie an, daß bei Indifferenz sowohl Eva als auch Maria stets möglichst viel kaufen. Ferner kaufen Eva
und Maria Himbeerbrause ausschließlich bei Anna,
die Himbeerbrause zu Grenzkosten von Null herstellen kann und risikoneutral ist. Anna kennt auch die
Nachfragen von Eva und Maria kann aber die beiden Zwillinge nicht unterscheiden. Die Wahrscheinlichkeit, daß entweder Eva oder Maria Kundin ist,
ist jeweils 12 .
• Wenn Anna einen festen Preis für jedes Glas
Himbeerbrause verlangt, macht sie den größten
Gewinn mit einem Preis von etwa. . . (11 Punkte)
b
c
d
e
20
25
32
15
11: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
3
1
4
40
15
3
1
4
60
20
2
0
2
40
25
1
0
1
25
32
1
0
1
32
Der Einfachheit halber berechnen wir den Gewinn
aus zwei Verkäufen. Wir sehen, daß der Gewinn
bei einem Preis vom 15 am höchsten ist.
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, daß sie aber
unterschiedliche Preise für das erste, zweite und
dritte Glas, das ein Zwilling kauft, verlangen
kann. In diesem Fall wird sie für das erste Glas
den folgenden Preis verlangen. . .
(7 Punkte)
b
c
d
e
25
32
15
20
12: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
1
1
2
20
15
1
1
2
30
20
1
0
1
20
25
1
0
1
25
32
1
0
1
32
Der Gewinn ist also bei einem Preis vom 32 am
höchsten.
• . . . und für das zweite Glas. . .
b
c
32
15
13: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
20
20
1
0
1
20
(7 Punkte)
e
25
25
0
0
0
0
32
0
0
0
0
Der Gewinn ist also bei einem Preis vom 20 am
höchsten.
• . . . und für das dritte Glas. . .
b
c
15
20
14: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
25
20
0
0
0
0
25
0
0
0
0
32
0
0
0
0
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, und auch nicht
unterschiedliche Preise für das erste, zweite und
dritte Glas, das eine Kundin kauft, verlangen
kann. Sie kann aber unterschiedliche Güterbündel
anbieten. Jede Kundin kann zu den angegebenen
Preisen beliebig viele Güterbündel kaufen. Geben
Sie alle Güterbündel an, die Anna im Gewinnmaximum anbieten kann (mehrere Antworten
möglich):
(45 Punkte)
1 Glas zum Preis von 15
2 Gläser zum Preis von 52
3 Gläser zum Preis von 32
3 Gläser zum Preis von 67
1 Glas zum Preis von 20
Nehmen wir zunächst an, Anna würde jeweils nur
1
15
3
1
4
45
Menge
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
1
20
2
0
2
40
2
52
1
0
1
52
3
32
1
0
1
32
3
67
1
0
1
67
Der Gewinn ist also bei 3 Gläsern zum Preis
von 67 am höchsten. Die Zahlungsbereitschaft von
Eva wird vollständig abgeschöpft. Wir sehen aber,
daß Anna auch noch das Bündel 2 Gläser zum
”
Preis von 52“ anbieten kann. Auch hier wird
die Zahlungsbereitschaft von Eva vollständig abgeschöpft, sie ist also indifferent, und kauft deshalb annahmegemäß das Bündel zum Preis von
67.
Aufgabe:
Betrachten Sie das folgende Spiel (Auszahlungen von Spieler 1 stehen links unten, Auszahlungen von Spieler 2 stehen rechts oben):
l
t
Spieler
1
(7 Punkte)
e
32
Der Gewinn ist also bei einem Preis vom 15 am
höchsten.
15a:
15b:
15c:
15d:
15e:
ein Güterbündel anbieten:
m
b
1
4
2
Spieler 2
c
2
1
2
0
5
7
2
3
0
r
3
8
1
5
2
t
m
Spieler2
c
r
1
3
2
8
5
1
7
5
finden wir die beiden obigen Gleichgewichte. (5, 1)
und (8, 3) sind keine Notation für Gleichgewichte.
• Im gemischten Gleichgewicht werden die Strategien mit folgenden Wahrscheinlichkeiten gespielt
(mehrere Antworten möglich)
(60 Punkte)
17a:
17b:
17c:
17d:
(l, c, r) mit (0, 38 , 58 )
(t, m, b) mit ( 14 , 34 , 0)
(t, m, b) mit ( 23 , 0, 13 )
(l, c, r) mit ( 58 , 38 , 0)
πm =
3
8
·7+
5
8
·5 =
46
.
8
Spieler 2 wird durch (t, m, b) mit ( 23 , 13 , 0) indifferent zwischen c und r:
πc = 23 · 1 + 13 · 5 = 73
πr = 23 · 3 + 13 · 1 = 73
Diese beiden gemischen Strategien bilden also ein
Gleichgewicht.
Die gemischte Strategie (t, m, b) mit ( 14 , 34 , 0)
macht Spieler 2 nicht indifferent, er wird immer
c spielen, dann aber wird Spieler 1 nicht mehr
mischen wollen.
Aufgabe:
A verkauft eine Einheit eines unteilbaren Gutes an B. A weiß, dass B eine Zahlungsbereitsschaft von 5 hat. Der Preis bestimmt sich über
folgendes Spiel: Zuerst schlägt A dem B einen Preis
p ∈ vor. Wenn dann B annimmt, hat A den Nutzen p und B hat den Nutzen 5 − p. Wenn B nicht
annimmt, haben beide einen Nutzen von 0.
Welche der folgenden Aussagen sind wahr (mehrere
Antworten möglich):
(65 Punkte)
Das Spiel ist sequentiell, d.h. wir verwenden
Rückwärtsinduktion. Für jede Strategie von A muß
B eine beste Antwort spielen, gegeben diese Strategie
von B muß dann auch A eine beste Antwort spielen.
A wählt p = 5, B nimmt nur an, wenn p ≤ 5 ist ein
Gleichgewicht. Beide können sich durch abweichen
nur verschlechtern.
A wählt p = 52 B nimmt nur an, wenn p ≤ 52 ist kein
Gleichgewicht. In allen Fällen, in denen A einen
Preis p ∈ ( 52 , 5) wählt, spielt B keine beste Antwort.
A wählt p = 0, B nimmt nur an, wenn p ≤ 0 ist kein
Gleichgewicht, In allen Fällen, in denen A einen
Preis p ∈ (0, 5) wählt, spielt B keine beste Antwort.
A wählt p = 5, B nimmt nur an, wenn p < 5 ist
kein Gleichgewicht, A kann sich durch einen kleineren Preis verbessern.
A wählt p = 5, B nimmt nur an, wenn p ≤ 7 ist
kein Gleichgewicht, A kann sich durch einen höheren Preis verbessern.
Aufgabe:
Drei Löwen befinden sich vor einem
Beutetier. Wenn Löwe 1 das Tier nicht frisst, endet
das Spiel. Wenn Löwe 1 die Beute frisst, kann Löwe
2 sich entscheiden, ob er den Löwen 1 frisst. Wenn
nicht, endet das Spiel. Wenn ja, kann sich Löwe 3
entscheiden, ob er den Löwen 2 frisst oder nicht.
Die Auszahlungen bemessen sich für jedes Tier nach
folgender Tabelle:
4
• Bitte markieren Sie alle Gleichgewichte in reinen
Strategien (mehrere Antworten möglich, achten
Sie auf die richtige Schreibweise):
(40 Punkte)
16: a (5, 1) b (t, r) c (t, l) d (8, 3) e (m, c)
Spieler 1 wird nie b spielen, da diese Strategie
durch m strikt dominiert wird. Dann wird aber
Spieler 2 nie l spielen, da diese Strategie durch r
dominiert ist. In dem verbleibenden Spiel
Spieler1
17e: (t, m, b) mit ( 23 , 13 , 0)
Wir haben oben bereits gesehen, daß b und l nie
gespielt werden. Damit fallen bereits 2 der fünf
Möglichkeiten fort. Durch (l, c, r) mit (0, 38 , 58 )
wird Spieler 1 indifferent zwischen t und m:
πt = 38 · 2 + 58 · 8 = 46
8
18a: Wenn A einen Preis p = 5 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18b: Wenn A einen Preis p = 5 vorschlägt, ist es
eine beste Antwort von B nicht anzunehmen
18c: Wenn A einen Preis p = 5 vorschlägt, hat B
keine beste Antwort
18d: Wenn A einen Preis p = 52 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18e: Wenn A einen Preis p = 0 vorschlägt, ist es
eine beste Antwort von B anzunehmen
Wenn A einen Preis p = 5 vorschlägt hat B einen
Nutzen von 0, egal ob er annimmt oder ablehnt. Beides ist also eine beste Antwort. Wenn A einen Preis
p = 52 vorschlägt, bekommt B nichts wenn er ablehnt, aber 52 wenn er annimmt, also ist es beste
Antwort anzunehmen. Wenn A einen Preis p = 0
vorschlägt, bekommt B nichts wenn er ablehnt, aber
5 wenn er annimmt, also ist es beste Antwort anzunehmen.
Ein Gleichgewicht dieses Spiels ist (mehrere Antworten möglich):
(65 Punkte)
19a:
19b:
19c:
19d:
19e:
A
A
A
A
A
wählt
wählt
wählt
wählt
wählt
p=
p=
p=
p=
p=
0, B nimmt nur an, wenn p ≤ 0
5, B nimmt nur an, wenn p < 5
5, B nimmt nur an, wenn p ≤ 5
5, B nimmt nur an, wenn p ≤ 7
5
, B nimmt nur an, wenn p ≤ 52
2
fressen
nicht fressen
gefressen
werden
1
1
nicht gefressen werden
3
2
Welche der folgenden Aussagen gelten im Gleichgewicht (mehrere Antworten möglich):
(50 Punkte)
Löwe 1 wird immer fressen
Löwe 3 bekommt mehr als die anderen
Löwe 1 bekommt mehr als die anderen
Löwe 2 wird immer fressen, wenn er zum Zug
kommt
20e: Löwe 3 wird immer fressen, wenn er zum Zug
kommt
Wir lösen das Spiel durch Rückwärtsinduktion.
Nach Löwe 3 gibt es keinen weiteren Zug. Löwe
3 stellt sich besser wenn er frisst, also wird er immer fressen. Vor Löwe 3 kommt Löwe 2 zum Zug.
Er weiß nun, daß er immer gefressen wird, sollte
er selber fressen. Also wird er sich für nicht fres”
sen“ entscheiden, und das Spiel enden lassen. Vor
Löwe 2 kommt Löwe 1 zum Zug. Er weiß nun,
daß Löwe 2 nie fressen wird, er bekommt also eine
höhere Auszahlung, wenn er frißt.
20a:
20b:
20c:
20d:
maximal erreichbare Punktzahl: 587
davon durch Randomisieren erreichbar: 259.9
Version
—
Die Version bestimmt sich nur durch die beiden
Kreise ganz links.
Betrachten Sie einen Markt, in dem die
Konsumenten bei einem Preis P < 36 genau Q = 12
Einheiten nachfragen. Bei P = 36 fragen die Konsumenten jede angebotene Menge zwischen 0 und
12 nach. Steigt der Preis über P = 36 wird nichts
nachgefragt.
Aufgabe:
• Was können Sie über die Preiselastizität der
Nachfrage auf dieser Nachfragekurve sagen?
(8 Punkte)
1a: Die Nachfrage ist stets sehr elastisch
1b: Die Nachfrage ist stets sehr unelastisch
1c: Die Nachfrage ist unelastisch bei P < 36,
elastisch bei P = 36
1d: Die Nachfrage ist elastisch bei P < 36, unelastisch bei P = 36
1e: Die Nachfrageelastizität ist −1 bei P < 36
P
36
(unelastisch)
Nachfrage
(elastisch)
MC
12
Q
• Ein Monopolist in diesem Markt hat keine Fixkosten und Grenzkosten M C = Q (Die Grenzkosten
nennen wir M C, die Menge Q). Bei welcher der
folgenden Mengen erzielt der Monopolist den
größten Gewinn?
(10 Punkte)
b
c
d
e
12
20
36
10
2: a 6
P
36
Nachfrage
→
MC
P
36
Nachfrage
→
MC
12
Q
12
Q
Der Gewinn des Monopolisten ist durch die
Fläche zwischen Preis und Grenzkostenkurve gegeben. Diese Fläche wird maximal bei Q = 12.
• Der Gewinn ist in diesem Fall etwa. . .
(10 Punkte)
3:
0
a
b
360
c
480
d
Die obige Fläche bestimmt sich zu
180
e
240
36+(36−12)
2
· 12
• Die Konsumentenrente ist etwa. . . (12 Punkte)
b 480
c 180
d 240
e 360
4: a 0
Die Konsumentenrente ist die Fläche zwischen
Preis und Nachfragekurve — hier bleibt leider für
die Konsumenten nichts übrig.
• Nehmen Sie an, die Regierung könnte Preis und
Menge beliebig regulieren. Dadurch könnte die
Summe aus Produzentenrente und Konsumentenrente ungefähr um den folgenden Betrag gesteigert
werden. . .
(18 Punkte)
b
c
d
e 120
30
60
90
5: a 0
Die Summe aus Produzentenrente und Konsumentenrente ist die Fläche zwischen Nachfragekurve und Grenzkostenkurve. Die ist hier aber bereits ohne Regierungsintervention maximal.
• Nun betrachten Sie Mengenwettbewerb (Stackelberg) von zwei Anbietern. Erst produziert ein
Anbieter die Menge Q1 mit Grenzkosten von
M C = Q1 , dies beobachtet der zweite Anbieter
und produzert danach die Menge Q2 mit Grenzkosten M C = Q2 . Welche Menge wird der erste
Anbieter wählen?
(11 Punkte)
b
c
d
e
12
18
36
9
6: a 0
• Welche Menge wird der zweite Anbieter wählen?
(11 Punkte)
b
c
d
e
18
36
9
12
7: a 0
Der zweite Anbieter wird immer die Differenz
zwischen der Menge des ersten Anbieters und 12
produzieren. Gegeben dieses Verhalten ist es für
den ersten Anbieter optimal 12 zu wählen, der
zweite wird dann 0 wählen.
Für alle drei Produzenten ergibt sich der Gewinn
πi jeweils zu
π1
π2
π3
=
=
=
q1 · (30 − q1 − q2 − q3 )
q2 · (30 − q1 − q2 − q3 )
q3 · (24 − q1 − q2 − q3 )
damit ergeben sich die Ableitungen zu
dπ1 /dq1
dπ2 /dq2
dπ3 /dq3
=
=
=
30 − 2q1 − q2 − q3
30 − q1 − 2q2 − q3
24 − q1 − q2 − 2q3
Für jeden Produzenten im Markt muss die Ableitung Null sein. Daraus ergibt sich die Reaktionsfunktion
q1
q2
q3
=
=
=
(30 − q2 − q3 )/2
(30 − q1 − q3 )/2
(24 − q1 − q2 )/2
Diese Bedingungen sind erfüllt, wenn q1 = q2 = 9
und q3 = 3.
• B und C überlegen sich, ob es sich lohnt, in den
Markt einzutreten. Sie haben Markteintrittskosten KB bzw. KC . Betrachten Sie folgende Situation: Erst hat A die Möglichkeit, sich zu verpflichten, für den Fall des Markteintrittes von C die
Markteintrittskosten KC von C zu übernehmen.
Diese Entscheidung ist B und C bekannt. Danach
entscheiden sich B und C gleichzeitig, ob sie in den
Markt eintreten. Markieren Sie die notwendigen
Bedingungen, die gleichzeitig erfüllt sein müssen,
damit es ein Gleichgewicht gibt, in dem A die
Markteintrittskosten des C übernimmt (mehrere
Antworten möglich).
(50 Punkte)
9: aKB > 0 bKB > 81 cKB < 81 dKB < 100 eKB < 144
(50 Punkte)
10: aKC > 0 bKC < 36 cKC > 36 dKC < 44 eKC > 9
Die inverse Nachfrage nach Knorz sei
P = 31 − Q wobei P der Preis und Q die Menge
sind. Produzent A befindet sich allein im Markt und
hat Grenzkosten von 1. Es gibt zwei Konkurrenten,
B und C, die in den Markt eintreten können. Falls
sie das, einzeln oder alle beide, tun, stellen Sie das
gleiche Gut wie A her, und der Marktpreis bestimmt
sich durch Cournotwettbewerb. B hat Grenzkosten
von 1, C hat Grenzkosten von 7.
Wir bestimmen zunächst aus den obigen Reaktionsfunktionen Mengen für die möglichen Marktkonstellationen:
• Stellen Sie sich vor, B und C würden in den
Markt eintreten. Im Gleichgewicht gilt (mehrere
Antworten möglich):
(50 Punkte)
Daraus ergeben sich die Gewinne
Aufgabe:
8a:
8b:
8c:
8d:
8e:
A produziert mehr als 10 Einheiten
C produziert qC = 32
B produziert weniger als 10 Einheiten
A produziert genausoviel wie B
C produziert qC = 3
A, B, C
A, B
A, C
A
A, B, C
A, B
A, C
A
π1
81
100
144
225
q1
9
10
12
15
q2
9
10
0
0
π2
81 − KB
100 − KB
0
0
q3
3
0
6
0
π3
9 − KC
0
36 − KC
0
Nun können wir uns fragen, warum A die Kosten
des C übernehmen sollte. Irgendetwas muß sich für
ihn verbessern. Das ist aber nur der Fall, wenn wir
ohne Kostenübername in der Situation A, B sind. In
den drei anderen Situationen ist C entweder sowieso
schon im Markt, oder A bekommt bereits den maximal möglichen Gewinn. Wann aber sind wir in der
Situation A, B? Spieler B muß einen Anreiz haben,
einzutreten, d.h. 100−KB > 0. Spieler C muß einen
Anreiz haben, draußen zu bleiben, d.h. 9 − KC < 0.
Wenn nun A die Eintrittskosten des C übernimmt
sind die Gewinne
A, B, C
A, B
A, C
A
π1
81 − KC
100
144 − KC
225
π2
81 − KB
100 − KB
0
0
π3
9
0
36
0
Nun tritt C auf jeden Fall in den Markt ein. A verbessert sich aber nur, wenn B jetzt nicht mehr in
den Markt eintritt. Das macht B aber nur wenn
81 − KB < 0 Schließlich soll sich diese Aktion für A
auch lohnen, und das gibt uns die letzte Bedingung
144 − KC > 100.
Falls Sie in dieser Aufgabe neben den obigen Bedingungen auch redundante Bedingungen angegeben
haben (also z.B. KC > 9 und KC > 0), wird das
nicht als falsch bewertet.
Aufgabe:
Die Zwillinge Eva und Maria sind durstig und die einzigen Nachfragerinnen nach Himbeerbrause. Die Zahlungsbereitschaft von Eva sind 15
für das erste Glas, und 0 für alle weiteren Gläser.
Die Zahlungsbereitsschaft von Maria sind 32 für das
erste Glas, 20 für das zweite Glas, 15 für das dritte
Glas, und 0 für alle weiteren Gläser. Nehmen Sie an,
daß bei Indifferenz sowohl Eva als auch Maria stets
möglichst viel kaufen. Ferner kaufen Eva und Maria Himbeerbrause ausschließlich bei Anna, die Himbeerbrause zu Grenzkosten von Null herstellen kann
und risikoneutral ist. Anna kennt auch die Nachfragen von Eva und Maria kann aber die beiden Zwillinge nicht unterscheiden. Die Wahrscheinlichkeit, daß
entweder Eva oder Maria Kundin ist, ist jeweils 12 .
• Wenn Anna einen festen Preis für jedes Glas
Himbeerbrause verlangt, macht sie den größten
Gewinn mit einem Preis von etwa. . . (11 Punkte)
b
c
d
e
25
32
15
20
11: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
3
1
4
40
15
3
1
4
60
20
2
0
2
40
25
1
0
1
25
32
1
0
1
32
Der Einfachheit halber berechnen wir den Gewinn
aus zwei Verkäufen. Wir sehen, daß der Gewinn
bei einem Preis vom 15 am höchsten ist.
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, daß sie aber
unterschiedliche Preise für das erste, zweite und
dritte Glas, das ein Zwilling kauft, verlangen
kann. In diesem Fall wird sie für das erste Glas
den folgenden Preis verlangen. . .
(7 Punkte)
b
c
d
e
32
15
20
25
12: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
1
1
2
20
15
1
1
2
30
20
1
0
1
20
25
1
0
1
25
32
1
0
1
32
Der Gewinn ist also bei einem Preis vom 32 am
höchsten.
• . . . und für das zweite Glas. . .
b
c
15
20
13: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
25
20
1
0
1
20
(7 Punkte)
e
32
25
0
0
0
0
32
0
0
0
0
Der Gewinn ist also bei einem Preis vom 20 am
höchsten.
• . . . und für das dritte Glas. . .
b
c
20
25
14: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
32
20
0
0
0
0
25
0
0
0
0
32
0
0
0
0
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, und auch nicht
unterschiedliche Preise für das erste, zweite und
dritte Glas, das eine Kundin kauft, verlangen
kann. Sie kann aber unterschiedliche Güterbündel
anbieten. Jede Kundin kann zu den angegebenen
Preisen beliebig viele Güterbündel kaufen. Geben
Sie alle Güterbündel an, die Anna im Gewinnmaximum anbieten kann (mehrere Antworten
möglich):
(45 Punkte)
1 Glas zum Preis von 15
3 Gläser zum Preis von 32
3 Gläser zum Preis von 67
1 Glas zum Preis von 20
2 Gläser zum Preis von 52
Nehmen wir zunächst an, Anna würde jeweils nur
1
15
3
1
4
45
Menge
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
1
20
2
0
2
40
2
52
1
0
1
52
3
32
1
0
1
32
3
67
1
0
1
67
Der Gewinn ist also bei 3 Gläsern zum Preis
von 67 am höchsten. Die Zahlungsbereitschaft von
Maria wird vollständig abgeschöpft. Wir sehen
aber, daß Anna auch noch das Bündel 2 Gläser
”
zum Preis von 52“ anbieten kann. Auch hier wird
die Zahlungsbereitschaft von Maria vollständig
abgeschöpft, sie ist also indifferent, und kauft deshalb annahmegemäß das Bündel zum Preis von
67.
Aufgabe:
Betrachten Sie das folgende Spiel (Auszahlungen von Spieler 1 stehen links unten, Auszahlungen von Spieler 2 stehen rechts oben):
l
t
Spieler
1
(7 Punkte)
e
15
Der Gewinn ist also bei einem Preis vom 15 am
höchsten.
15a:
15b:
15c:
15d:
15e:
ein Güterbündel anbieten:
m
b
8
5
4
Spieler 2
c
3
1
2
1
5
7
2
3
0
r
2
1
0
4
2
t
m
Spieler2
c
l
1
3
2
8
5
1
7
5
finden wir die beiden obigen Gleichgewichte. (5, 1)
und (8, 3) sind keine Notation für Gleichgewichte.
• Im gemischten Gleichgewicht werden die Strategien mit folgenden Wahrscheinlichkeiten gespielt
(mehrere Antworten möglich)
(60 Punkte)
17a:
17b:
17c:
17d:
(l, c, r) mit ( 58 , 38 , 0)
(t, m, b) mit ( 23 , 0, 13 )
(l, c, r) mit (0, 38 , 58 )
(t, m, b) mit ( 23 , 13 , 0)
πm =
3
8
·7+
5
8
·5 =
46
.
8
Spieler 2 wird durch (t, m, b) mit ( 23 , 13 , 0) indifferent zwischen c und l:
πc = 23 · 1 + 13 · 5 = 73
πl = 23 · 3 + 13 · 1 = 73
Diese beiden gemischen Strategien bilden also ein
Gleichgewicht.
Die gemischte Strategie (t, m, b) mit ( 14 , 34 , 0)
macht Spieler 2 nicht indifferent, er wird immer
c spielen, dann aber wird Spieler 1 nicht mehr
mischen wollen.
Aufgabe:
A verkauft eine Einheit eines unteilbaren Gutes an B. A weiß, dass B eine Zahlungsbereitsschaft von 3 hat. Der Preis bestimmt sich über
folgendes Spiel: Zuerst schlägt A dem B einen Preis
p ∈ vor. Wenn dann B annimmt, hat A den Nutzen p und B hat den Nutzen 3 − p. Wenn B nicht
annimmt, haben beide einen Nutzen von 0.
Welche der folgenden Aussagen sind wahr (mehrere
Antworten möglich):
(65 Punkte)
Das Spiel ist sequentiell, d.h. wir verwenden
Rückwärtsinduktion. Für jede Strategie von A muß
B eine beste Antwort spielen, gegeben diese Strategie
von B muß dann auch A eine beste Antwort spielen.
A wählt p = 3, B nimmt nur an, wenn p ≤ 3 ist ein
Gleichgewicht. Beide können sich durch abweichen
nur verschlechtern.
A wählt p = 32 B nimmt nur an, wenn p ≤ 32 ist kein
Gleichgewicht. In allen Fällen, in denen A einen
Preis p ∈ ( 32 , 3) wählt, spielt B keine beste Antwort.
A wählt p = 0, B nimmt nur an, wenn p ≤ 0 ist kein
Gleichgewicht, In allen Fällen, in denen A einen
Preis p ∈ (0, 3) wählt, spielt B keine beste Antwort.
A wählt p = 3, B nimmt nur an, wenn p < 3 ist
kein Gleichgewicht, A kann sich durch einen kleineren Preis verbessern.
A wählt p = 3, B nimmt nur an, wenn p ≤ 7 ist
kein Gleichgewicht, A kann sich durch einen höheren Preis verbessern.
Aufgabe: Drei Tiger befinden sich vor einem Beutetier. Wenn Tiger 1 das Tier nicht frisst, endet das
Spiel. Wenn Tiger 1 die Beute frisst, kann Tiger
2 sich entscheiden, ob er den Tiger 1 frisst. Wenn
nicht, endet das Spiel. Wenn ja, kann sich Tiger 3
entscheiden, ob er den Tiger 2 frisst oder nicht. Die
Auszahlungen bemessen sich für jedes Tier nach folgender Tabelle:
2
• Bitte markieren Sie alle Gleichgewichte in reinen
Strategien (mehrere Antworten möglich, achten
Sie auf die richtige Schreibweise):
(40 Punkte)
16: a (5, 1) b (t, r) c (8, 3) d (m, c) e (t, l)
Spieler 1 wird nie b spielen, da diese Strategie
durch m strikt dominiert wird. Dann wird aber
Spieler 2 nie r spielen, da diese Strategie durch l
dominiert ist. In dem verbleibenden Spiel
Spieler1
17e: (t, m, b) mit ( 14 , 34 , 0)
Wir haben oben bereits gesehen, daß b und r nie
gespielt werden. Damit fallen bereits 2 der fünf
Möglichkeiten fort. Durch (l, c, r) mit ( 58 , 38 , 0)
wird Spieler 1 indifferent zwischen t und m:
πt = 38 · 2 + 58 · 8 = 46
8
18a: Wenn A einen Preis p = 3 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18b: Wenn A einen Preis p = 3 vorschlägt, hat B
keine beste Antwort
18c: Wenn A einen Preis p = 32 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18d: Wenn A einen Preis p = 0 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18e: Wenn A einen Preis p = 3 vorschlägt, ist es
eine beste Antwort von B nicht anzunehmen
Wenn A einen Preis p = 3 vorschlägt hat B einen
Nutzen von 0, egal ob er annimmt oder ablehnt. Beides ist also eine beste Antwort. Wenn A einen Preis
p = 32 vorschlägt, bekommt B nichts wenn er ablehnt, aber 32 wenn er annimmt, also ist es beste
Antwort anzunehmen. Wenn A einen Preis p = 0
vorschlägt, bekommt B nichts wenn er ablehnt, aber
3 wenn er annimmt, also ist es beste Antwort anzunehmen.
Ein Gleichgewicht dieses Spiels ist (mehrere Antworten möglich):
(65 Punkte)
19a:
19b:
19c:
19d:
19e:
A
A
A
A
A
wählt
wählt
wählt
wählt
wählt
p=
p=
p=
p=
p=
0, B nimmt nur an, wenn p ≤ 0
3, B nimmt nur an, wenn p ≤ 3
3, B nimmt nur an, wenn p ≤ 7
3
, B nimmt nur an, wenn p ≤ 32
2
3, B nimmt nur an, wenn p < 3
fressen
nicht fressen
gefressen
werden
1
1
nicht gefressen werden
3
2
Welche der folgenden Aussagen gelten im Gleichgewicht (mehrere Antworten möglich):
(50 Punkte)
20a: Tiger 1 wird immer fressen
20b: Tiger 1 bekommt mehr als die anderen
20c: Tiger 2 wird immer fressen, wenn er zum Zug
kommt
20d: Tiger 3 wird immer fressen, wenn er zum Zug
kommt
20e: Tiger 3 bekommt mehr als die anderen
Wir lösen das Spiel durch Rückwärtsinduktion.
Nach Tiger 3 gibt es keinen weiteren Zug. Tiger
3 stellt sich besser wenn er frisst, also wird er immer fressen. Vor Tiger 3 kommt Tiger 2 zum Zug.
Er weiß nun, daß er immer gefressen wird, sollte er
selber fressen. Also wird er sich für nicht fressen“
”
entscheiden, und das Spiel enden lassen. Vor Tiger
2 kommt Tiger 1 zum Zug. Er weiß nun, daß Tiger 2 nie fressen wird, er bekommt also eine höhere
Auszahlung, wenn er frißt.
maximal erreichbare Punktzahl: 587
davon durch Randomisieren erreichbar: 259.9
Version
—
Die Version bestimmt sich nur durch die beiden
Kreise ganz links.
Betrachten Sie einen Markt, in dem die
Konsumenten bei einem Preis P < 30 genau Q = 10
Einheiten nachfragen. Bei P = 30 fragen die Konsumenten jede angebotene Menge zwischen 0 und
10 nach. Steigt der Preis über P = 30 wird nichts
nachgefragt.
Aufgabe:
• Was können Sie über die Preiselastizität der
Nachfrage auf dieser Nachfragekurve sagen?
(8 Punkte)
1a: Die Nachfrage ist stets sehr elastisch
1b: Die Nachfrage ist unelastisch bei P < 30,
elastisch bei P = 30
1c: Die Nachfrage ist elastisch bei P < 30, unelastisch bei P = 30
1d: Die Nachfrageelastizität ist −1 bei P < 30
1e: Die Nachfrage ist stets sehr unelastisch
P
30
(unelastisch)
Nachfrage
(elastisch)
MC
10
Q
• Ein Monopolist in diesem Markt hat keine Fixkosten und Grenzkosten M C = Q (Die Grenzkosten
nennen wir M C, die Menge Q). Bei welcher der
folgenden Mengen erzielt der Monopolist den
größten Gewinn?
(10 Punkte)
b
c
d 7.5
e
15
30
10
2: a 5
P
30
Nachfrage
→
MC
P
30
Nachfrage
→
MC
10
Q
10
Q
Der Gewinn des Monopolisten ist durch die
Fläche zwischen Preis und Grenzkostenkurve gegeben. Diese Fläche wird maximal bei Q = 10.
• Der Gewinn ist in diesem Fall etwa. . .
(10 Punkte)
3:
0
a
b
300
c
150
d
Die obige Fläche bestimmt sich zu
200
e
250
30+(30−10)
2
· 10
• Die Konsumentenrente ist etwa. . . (12 Punkte)
b 150
c 200
d 250
e 300
4: a 0
Die Konsumentenrente ist die Fläche zwischen
Preis und Nachfragekurve — hier bleibt leider für
die Konsumenten nichts übrig.
• Nehmen Sie an, die Regierung könnte Preis und
Menge beliebig regulieren. Dadurch könnte die
Summe aus Produzentenrente und Konsumentenrente ungefähr um den folgenden Betrag gesteigert
werden. . .
(18 Punkte)
b
c
d 100
e
50
75
25
5: a 0
Die Summe aus Produzentenrente und Konsumentenrente ist die Fläche zwischen Nachfragekurve und Grenzkostenkurve. Die ist hier aber bereits ohne Regierungsintervention maximal.
• Nun betrachten Sie Mengenwettbewerb (Stackelberg) von zwei Anbietern. Erst produziert ein
Anbieter die Menge Q1 mit Grenzkosten von
M C = Q1 , dies beobachtet der zweite Anbieter
und produzert danach die Menge Q2 mit Grenzkosten M C = Q2 . Welche Menge wird der erste
Anbieter wählen?
(11 Punkte)
b
c
d 7.5
e
15
30
10
6: a 0
• Welche Menge wird der zweite Anbieter wählen?
(11 Punkte)
b
c 7.5
d
e
30
10
15
7: a 0
Der zweite Anbieter wird immer die Differenz
zwischen der Menge des ersten Anbieters und 10
produzieren. Gegeben dieses Verhalten ist es für
den ersten Anbieter optimal 10 zu wählen, der
zweite wird dann 0 wählen.
Für alle drei Produzenten ergibt sich der Gewinn
πi jeweils zu
π1
π2
π3
=
=
=
q1 · (30 − q1 − q2 − q3 )
q2 · (30 − q1 − q2 − q3 )
q3 · (24 − q1 − q2 − q3 )
damit ergeben sich die Ableitungen zu
dπ1 /dq1
dπ2 /dq2
dπ3 /dq3
=
=
=
30 − 2q1 − q2 − q3
30 − q1 − 2q2 − q3
24 − q1 − q2 − 2q3
Für jeden Produzenten im Markt muss die Ableitung Null sein. Daraus ergibt sich die Reaktionsfunktion
q1
q2
q3
=
=
=
(30 − q2 − q3 )/2
(30 − q1 − q3 )/2
(24 − q1 − q2 )/2
Diese Bedingungen sind erfüllt, wenn q1 = q2 = 9
und q3 = 3.
• B und C überlegen sich, ob es sich lohnt, in den
Markt einzutreten. Sie haben Markteintrittskosten KB bzw. KC . Betrachten Sie folgende Situation: Erst hat A die Möglichkeit, sich zu verpflichten, für den Fall des Markteintrittes von C die
Markteintrittskosten KC von C zu übernehmen.
Diese Entscheidung ist B und C bekannt. Danach
entscheiden sich B und C gleichzeitig, ob sie in den
Markt eintreten. Markieren Sie die notwendigen
Bedingungen, die gleichzeitig erfüllt sein müssen,
damit es ein Gleichgewicht gibt, in dem A die
Markteintrittskosten des C übernimmt (mehrere
Antworten möglich).
(50 Punkte)
9: aKB > 0 bKB < 81 cKB < 100 dKB < 144 eKB > 81
(50 Punkte)
10: aKC > 0 bKC > 36 cKC < 44 dKC > 9 eKC < 36
Die inverse Nachfrage nach Knorz sei
P = 31 − Q wobei P der Preis und Q die Menge
sind. Produzent A befindet sich allein im Markt und
hat Grenzkosten von 1. Es gibt zwei Konkurrenten,
B und C, die in den Markt eintreten können. Falls
sie das, einzeln oder alle beide, tun, stellen Sie das
gleiche Gut wie A her, und der Marktpreis bestimmt
sich durch Cournotwettbewerb. B hat Grenzkosten
von 1, C hat Grenzkosten von 7.
Wir bestimmen zunächst aus den obigen Reaktionsfunktionen Mengen für die möglichen Marktkonstellationen:
• Stellen Sie sich vor, B und C würden in den
Markt eintreten. Im Gleichgewicht gilt (mehrere
Antworten möglich):
(50 Punkte)
Daraus ergeben sich die Gewinne
Aufgabe:
8a:
8b:
8c:
8d:
8e:
A produziert mehr als 10 Einheiten
B produziert weniger als 10 Einheiten
A produziert genausoviel wie B
C produziert qC = 3
C produziert qC = 32
A, B, C
A, B
A, C
A
A, B, C
A, B
A, C
A
π1
81
100
144
225
q1
9
10
12
15
q2
9
10
0
0
π2
81 − KB
100 − KB
0
0
q3
3
0
6
0
π3
9 − KC
0
36 − KC
0
Nun können wir uns fragen, warum A die Kosten
des C übernehmen sollte. Irgendetwas muß sich für
ihn verbessern. Das ist aber nur der Fall, wenn wir
ohne Kostenübername in der Situation A, B sind. In
den drei anderen Situationen ist C entweder sowieso
schon im Markt, oder A bekommt bereits den maximal möglichen Gewinn. Wann aber sind wir in der
Situation A, B? Spieler B muß einen Anreiz haben,
einzutreten, d.h. 100−KB > 0. Spieler C muß einen
Anreiz haben, draußen zu bleiben, d.h. 9 − KC < 0.
Wenn nun A die Eintrittskosten des C übernimmt
sind die Gewinne
A, B, C
A, B
A, C
A
π1
81 − KC
100
144 − KC
225
π2
81 − KB
100 − KB
0
0
π3
9
0
36
0
Nun tritt C auf jeden Fall in den Markt ein. A verbessert sich aber nur, wenn B jetzt nicht mehr in
den Markt eintritt. Das macht B aber nur wenn
81 − KB < 0 Schließlich soll sich diese Aktion für A
auch lohnen, und das gibt uns die letzte Bedingung
144 − KC > 100.
Falls Sie in dieser Aufgabe neben den obigen Bedingungen auch redundante Bedingungen angegeben
haben (also z.B. KC > 9 und KC > 0), wird das
nicht als falsch bewertet.
Aufgabe:
Die Zwillinge Eva und Maria sind durstig und die einzigen Nachfragerinnen nach Himbeerbrause. Die Zahlungsbereitschaft von Eva sind 32
für das erste Glas, 20 für das zweite Glas, 15 für
das dritte Glas, und 0 für alle weiteren Gläser. Die
Zahlungsbereitsschaft von Maria sind 15 für das erste Glas, und 0 für alle weiteren Gläser. Nehmen
Sie an, daß bei Indifferenz sowohl Eva als auch Maria stets möglichst viel kaufen. Ferner kaufen Eva
und Maria Himbeerbrause ausschließlich bei Anna,
die Himbeerbrause zu Grenzkosten von Null herstellen kann und risikoneutral ist. Anna kennt auch die
Nachfragen von Eva und Maria kann aber die beiden Zwillinge nicht unterscheiden. Die Wahrscheinlichkeit, daß entweder Eva oder Maria Kundin ist,
ist jeweils 12 .
• Wenn Anna einen festen Preis für jedes Glas
Himbeerbrause verlangt, macht sie den größten
Gewinn mit einem Preis von etwa. . . (11 Punkte)
b
c
d
e
32
15
20
25
11: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
3
1
4
40
15
3
1
4
60
20
2
0
2
40
25
1
0
1
25
32
1
0
1
32
Der Einfachheit halber berechnen wir den Gewinn
aus zwei Verkäufen. Wir sehen, daß der Gewinn
bei einem Preis vom 15 am höchsten ist.
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, daß sie aber
unterschiedliche Preise für das erste, zweite und
dritte Glas, das ein Zwilling kauft, verlangen
kann. In diesem Fall wird sie für das erste Glas
den folgenden Preis verlangen. . .
(7 Punkte)
b
c
d
e
15
20
25
32
12: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
1
1
2
20
15
1
1
2
30
20
1
0
1
20
25
1
0
1
25
32
1
0
1
32
Der Gewinn ist also bei einem Preis vom 32 am
höchsten.
• . . . und für das zweite Glas. . .
b
c
20
25
13: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
32
20
1
0
1
20
(7 Punkte)
e
15
25
0
0
0
0
32
0
0
0
0
Der Gewinn ist also bei einem Preis vom 20 am
höchsten.
• . . . und für das dritte Glas. . .
b
c
25
32
14: a 10
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
15
20
0
0
0
0
25
0
0
0
0
32
0
0
0
0
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, und auch nicht
unterschiedliche Preise für das erste, zweite und
dritte Glas, das eine Kundin kauft, verlangen
kann. Sie kann aber unterschiedliche Güterbündel
anbieten. Jede Kundin kann zu den angegebenen
Preisen beliebig viele Güterbündel kaufen. Geben
Sie alle Güterbündel an, die Anna im Gewinnmaximum anbieten kann (mehrere Antworten
möglich):
(45 Punkte)
1 Glas zum Preis von 15
3 Gläser zum Preis von 67
1 Glas zum Preis von 20
2 Gläser zum Preis von 52
3 Gläser zum Preis von 32
Nehmen wir zunächst an, Anna würde jeweils nur
1
15
3
1
4
45
Menge
Preis
Konsum Eva
Konsum Maria
Konsum gesamt
2× Gewinn
1
20
2
0
2
40
2
52
1
0
1
52
3
32
1
0
1
32
3
67
1
0
1
67
Der Gewinn ist also bei 3 Gläsern zum Preis
von 67 am höchsten. Die Zahlungsbereitschaft von
Eva wird vollständig abgeschöpft. Wir sehen aber,
daß Anna auch noch das Bündel 2 Gläser zum
”
Preis von 52“ anbieten kann. Auch hier wird
die Zahlungsbereitschaft von Eva vollständig abgeschöpft, sie ist also indifferent, und kauft deshalb annahmegemäß das Bündel zum Preis von
67.
Aufgabe:
Betrachten Sie das folgende Spiel (Auszahlungen von Spieler 1 stehen links unten, Auszahlungen von Spieler 2 stehen rechts oben):
l
t
Spieler
1
(7 Punkte)
e
20
Der Gewinn ist also bei einem Preis vom 15 am
höchsten.
15a:
15b:
15c:
15d:
15e:
ein Güterbündel anbieten:
m
b
1
4
2
Spieler 2
c
2
1
2
0
5
7
2
3
0
r
3
8
1
5
2
t
m
Spieler2
c
r
1
3
2
8
5
1
7
5
finden wir die beiden obigen Gleichgewichte. (5, 1)
und (8, 3) sind keine Notation für Gleichgewichte.
• Im gemischten Gleichgewicht werden die Strategien mit folgenden Wahrscheinlichkeiten gespielt
(mehrere Antworten möglich)
(60 Punkte)
17a:
17b:
17c:
17d:
(l, c, r) mit (0, 38 , 58 )
(l, c, r) mit ( 58 , 38 , 0)
(t, m, b) mit ( 23 , 13 , 0)
(t, m, b) mit ( 14 , 34 , 0)
πm =
3
8
·7+
5
8
·5 =
46
.
8
Spieler 2 wird durch (t, m, b) mit ( 23 , 13 , 0) indifferent zwischen c und r:
πc = 23 · 1 + 13 · 5 = 73
πr = 23 · 3 + 13 · 1 = 73
Diese beiden gemischen Strategien bilden also ein
Gleichgewicht.
Die gemischte Strategie (t, m, b) mit ( 14 , 34 , 0)
macht Spieler 2 nicht indifferent, er wird immer
c spielen, dann aber wird Spieler 1 nicht mehr
mischen wollen.
Aufgabe:
A verkauft eine Einheit eines unteilbaren Gutes an B. A weiß, dass B eine Zahlungsbereitsschaft von 5 hat. Der Preis bestimmt sich über
folgendes Spiel: Zuerst schlägt A dem B einen Preis
p ∈ vor. Wenn dann B annimmt, hat A den Nutzen p und B hat den Nutzen 5 − p. Wenn B nicht
annimmt, haben beide einen Nutzen von 0.
Welche der folgenden Aussagen sind wahr (mehrere
Antworten möglich):
(65 Punkte)
Das Spiel ist sequentiell, d.h. wir verwenden
Rückwärtsinduktion. Für jede Strategie von A muß
B eine beste Antwort spielen, gegeben diese Strategie
von B muß dann auch A eine beste Antwort spielen.
A wählt p = 5, B nimmt nur an, wenn p ≤ 5 ist ein
Gleichgewicht. Beide können sich durch abweichen
nur verschlechtern.
A wählt p = 52 B nimmt nur an, wenn p ≤ 52 ist kein
Gleichgewicht. In allen Fällen, in denen A einen
Preis p ∈ ( 52 , 5) wählt, spielt B keine beste Antwort.
A wählt p = 0, B nimmt nur an, wenn p ≤ 0 ist kein
Gleichgewicht, In allen Fällen, in denen A einen
Preis p ∈ (0, 5) wählt, spielt B keine beste Antwort.
A wählt p = 5, B nimmt nur an, wenn p < 5 ist
kein Gleichgewicht, A kann sich durch einen kleineren Preis verbessern.
A wählt p = 5, B nimmt nur an, wenn p ≤ 7 ist
kein Gleichgewicht, A kann sich durch einen höheren Preis verbessern.
Aufgabe:
Drei Bären befinden sich vor einem
Beutetier. Wenn Bär 1 das Tier nicht frisst, endet das Spiel. Wenn Bär 1 die Beute frisst, kann
Bär 2 sich entscheiden, ob er den Bären 1 frisst.
Wenn nicht, endet das Spiel. Wenn ja, kann sich Bär
3 entscheiden, ob er den Bären 2 frisst oder nicht.
Die Auszahlungen bemessen sich für jedes Tier nach
folgender Tabelle:
4
• Bitte markieren Sie alle Gleichgewichte in reinen
Strategien (mehrere Antworten möglich, achten
Sie auf die richtige Schreibweise):
(40 Punkte)
16: a (5, 1) b (8, 3) c (m, c) d (t, r) e (t, l)
Spieler 1 wird nie b spielen, da diese Strategie
durch m strikt dominiert wird. Dann wird aber
Spieler 2 nie l spielen, da diese Strategie durch r
dominiert ist. In dem verbleibenden Spiel
Spieler1
17e: (t, m, b) mit ( 23 , 0, 13 )
Wir haben oben bereits gesehen, daß b und l nie
gespielt werden. Damit fallen bereits 2 der fünf
Möglichkeiten fort. Durch (l, c, r) mit (0, 38 , 58 )
wird Spieler 1 indifferent zwischen t und m:
πt = 38 · 2 + 58 · 8 = 46
8
18a: Wenn A einen Preis p = 5 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18b: Wenn A einen Preis p = 52 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18c: Wenn A einen Preis p = 0 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18d: Wenn A einen Preis p = 5 vorschlägt, ist es
eine beste Antwort von B nicht anzunehmen
18e: Wenn A einen Preis p = 5 vorschlägt, hat B
keine beste Antwort
Wenn A einen Preis p = 5 vorschlägt hat B einen
Nutzen von 0, egal ob er annimmt oder ablehnt. Beides ist also eine beste Antwort. Wenn A einen Preis
p = 52 vorschlägt, bekommt B nichts wenn er ablehnt, aber 52 wenn er annimmt, also ist es beste
Antwort anzunehmen. Wenn A einen Preis p = 0
vorschlägt, bekommt B nichts wenn er ablehnt, aber
5 wenn er annimmt, also ist es beste Antwort anzunehmen.
Ein Gleichgewicht dieses Spiels ist (mehrere Antworten möglich):
(65 Punkte)
19a:
19b:
19c:
19d:
19e:
A
A
A
A
A
wählt
wählt
wählt
wählt
wählt
p=
p=
p=
p=
p=
0, B nimmt nur an, wenn p ≤ 0
5, B nimmt nur an, wenn p ≤ 7
5
, B nimmt nur an, wenn p ≤ 52
2
5, B nimmt nur an, wenn p < 5
5, B nimmt nur an, wenn p ≤ 5
fressen
nicht fressen
gefressen
werden
1
1
nicht gefressen werden
3
2
Welche der folgenden Aussagen gelten im Gleichgewicht (mehrere Antworten möglich):
(50 Punkte)
20a: Bär 1 wird immer fressen
20b: Bär 2 wird immer fressen, wenn er zum Zug
kommt
20c: Bär 3 wird immer fressen, wenn er zum Zug
kommt
20d: Bär 3 bekommt mehr als die anderen
20e: Bär 1 bekommt mehr als die anderen
Wir lösen das Spiel durch Rückwärtsinduktion.
Nach Bär 3 gibt es keinen weiteren Zug. Bär 3
stellt sich besser wenn er frisst, also wird er immer
fressen. Vor Bär 3 kommt Bär 2 zum Zug. Er weiß
nun, daß er immer gefressen wird, sollte er selber
fressen. Also wird er sich für nicht fressen“ ent”
scheiden, und das Spiel enden lassen. Vor Bär 2
kommt Bär 1 zum Zug. Er weiß nun, daß Bär 2
nie fressen wird, er bekommt also eine höhere Auszahlung, wenn er frißt.
maximal erreichbare Punktzahl: 587
davon durch Randomisieren erreichbar: 259.9
Version
—
Die Version bestimmt sich nur durch die beiden
Kreise ganz links.
Betrachten Sie einen Markt, in dem die
Konsumenten bei einem Preis P < 36 genau Q = 12
Einheiten nachfragen. Bei P = 36 fragen die Konsumenten jede angebotene Menge zwischen 0 und
12 nach. Steigt der Preis über P = 36 wird nichts
nachgefragt.
Aufgabe:
• Was können Sie über die Preiselastizität der
Nachfrage auf dieser Nachfragekurve sagen?
(8 Punkte)
1a: Die Nachfrage ist stets sehr elastisch
1b: Die Nachfrage ist elastisch bei P < 36, unelastisch bei P = 36
1c: Die Nachfrageelastizität ist −1 bei P < 36
1d: Die Nachfrage ist stets sehr unelastisch
1e: Die Nachfrage ist unelastisch bei P < 36,
elastisch bei P = 36
P
36
(unelastisch)
Nachfrage
(elastisch)
MC
12
Q
• Ein Monopolist in diesem Markt hat keine Fixkosten und Grenzkosten M C = Q (Die Grenzkosten
nennen wir M C, die Menge Q). Bei welcher der
folgenden Mengen erzielt der Monopolist den
größten Gewinn?
(10 Punkte)
b
c
d
e
36
10
12
20
2: a 6
P
36
P
36
Nachfrage
→
Nachfrage
→
MC
MC
12
Q
12
Q
Der Gewinn des Monopolisten ist durch die
Fläche zwischen Preis und Grenzkostenkurve gegeben. Diese Fläche wird maximal bei Q = 12.
• Der Gewinn ist in diesem Fall etwa. . .
(10 Punkte)
3:
0
a
b
180
c
240
d
Die obige Fläche bestimmt sich zu
360
e
480
36+(36−12)
2
· 12
• Die Konsumentenrente ist etwa. . . (12 Punkte)
b 240
c 360
d 480
e 180
4: a 0
Die Konsumentenrente ist die Fläche zwischen
Preis und Nachfragekurve — hier bleibt leider für
die Konsumenten nichts übrig.
• Nehmen Sie an, die Regierung könnte Preis und
Menge beliebig regulieren. Dadurch könnte die
Summe aus Produzentenrente und Konsumentenrente ungefähr um den folgenden Betrag gesteigert
werden. . .
(18 Punkte)
b
c 120
d
e
90
30
60
5: a 0
Die Summe aus Produzentenrente und Konsumentenrente ist die Fläche zwischen Nachfragekurve und Grenzkostenkurve. Die ist hier aber bereits ohne Regierungsintervention maximal.
• Nun betrachten Sie Mengenwettbewerb (Stackelberg) von zwei Anbietern. Erst produziert ein
Anbieter die Menge Q1 mit Grenzkosten von
M C = Q1 , dies beobachtet der zweite Anbieter
und produzert danach die Menge Q2 mit Grenzkosten M C = Q2 . Welche Menge wird der erste
Anbieter wählen?
(11 Punkte)
b
c
d
e
36
9
12
18
6: a 0
• Welche Menge wird der zweite Anbieter wählen?
(11 Punkte)
b
c
d
e
9
12
18
36
7: a 0
Der zweite Anbieter wird immer die Differenz
zwischen der Menge des ersten Anbieters und 12
produzieren. Gegeben dieses Verhalten ist es für
den ersten Anbieter optimal 12 zu wählen, der
zweite wird dann 0 wählen.
Für alle drei Produzenten ergibt sich der Gewinn
πi jeweils zu
π1
π2
π3
=
=
=
q1 · (30 − q1 − q2 − q3 )
q2 · (30 − q1 − q2 − q3 )
q3 · (24 − q1 − q2 − q3 )
damit ergeben sich die Ableitungen zu
dπ1 /dq1
dπ2 /dq2
dπ3 /dq3
=
=
=
30 − 2q1 − q2 − q3
30 − q1 − 2q2 − q3
24 − q1 − q2 − 2q3
Für jeden Produzenten im Markt muss die Ableitung Null sein. Daraus ergibt sich die Reaktionsfunktion
q1
q2
q3
=
=
=
(30 − q2 − q3 )/2
(30 − q1 − q3 )/2
(24 − q1 − q2 )/2
Diese Bedingungen sind erfüllt, wenn q1 = q2 = 9
und q3 = 3.
• B und C überlegen sich, ob es sich lohnt, in den
Markt einzutreten. Sie haben Markteintrittskosten KB bzw. KC . Betrachten Sie folgende Situation: Erst hat A die Möglichkeit, sich zu verpflichten, für den Fall des Markteintrittes von C die
Markteintrittskosten KC von C zu übernehmen.
Diese Entscheidung ist B und C bekannt. Danach
entscheiden sich B und C gleichzeitig, ob sie in den
Markt eintreten. Markieren Sie die notwendigen
Bedingungen, die gleichzeitig erfüllt sein müssen,
damit es ein Gleichgewicht gibt, in dem A die
Markteintrittskosten des C übernimmt (mehrere
Antworten möglich).
(50 Punkte)
9: aKB > 0 bKB < 100 cKB < 144 dKB > 81 eKB < 81
(50 Punkte)
10: aKC > 0 bKC < 44 cKC > 9 dKC < 36 eKC > 36
Die inverse Nachfrage nach Knorz sei
P = 31 − Q wobei P der Preis und Q die Menge
sind. Produzent A befindet sich allein im Markt und
hat Grenzkosten von 1. Es gibt zwei Konkurrenten,
B und C, die in den Markt eintreten können. Falls
sie das, einzeln oder alle beide, tun, stellen Sie das
gleiche Gut wie A her, und der Marktpreis bestimmt
sich durch Cournotwettbewerb. B hat Grenzkosten
von 1, C hat Grenzkosten von 7.
Wir bestimmen zunächst aus den obigen Reaktionsfunktionen Mengen für die möglichen Marktkonstellationen:
• Stellen Sie sich vor, B und C würden in den
Markt eintreten. Im Gleichgewicht gilt (mehrere
Antworten möglich):
(50 Punkte)
Daraus ergeben sich die Gewinne
Aufgabe:
8a:
8b:
8c:
8d:
8e:
A produziert mehr als 10 Einheiten
A produziert genausoviel wie B
C produziert qC = 3
C produziert qC = 32
B produziert weniger als 10 Einheiten
A, B, C
A, B
A, C
A
A, B, C
A, B
A, C
A
π1
81
100
144
225
q1
9
10
12
15
q2
9
10
0
0
π2
81 − KB
100 − KB
0
0
q3
3
0
6
0
π3
9 − KC
0
36 − KC
0
Nun können wir uns fragen, warum A die Kosten
des C übernehmen sollte. Irgendetwas muß sich für
ihn verbessern. Das ist aber nur der Fall, wenn wir
ohne Kostenübername in der Situation A, B sind. In
den drei anderen Situationen ist C entweder sowieso
schon im Markt, oder A bekommt bereits den maximal möglichen Gewinn. Wann aber sind wir in der
Situation A, B? Spieler B muß einen Anreiz haben,
einzutreten, d.h. 100−KB > 0. Spieler C muß einen
Anreiz haben, draußen zu bleiben, d.h. 9 − KC < 0.
Wenn nun A die Eintrittskosten des C übernimmt
sind die Gewinne
A, B, C
A, B
A, C
A
π1
81 − KC
100
144 − KC
225
π2
81 − KB
100 − KB
0
0
π3
9
0
36
0
Nun tritt C auf jeden Fall in den Markt ein. A verbessert sich aber nur, wenn B jetzt nicht mehr in
den Markt eintritt. Das macht B aber nur wenn
81 − KB < 0 Schließlich soll sich diese Aktion für A
auch lohnen, und das gibt uns die letzte Bedingung
144 − KC > 100.
Falls Sie in dieser Aufgabe neben den obigen Bedingungen auch redundante Bedingungen angegeben
haben (also z.B. KC > 9 und KC > 0), wird das
nicht als falsch bewertet.
Aufgabe:
Die Zwillinge Eva und Maria sind durstig und die einzigen Nachfragerinnen nach Himbeerbrause. Die Zahlungsbereitschaft von Eva sind 15
für das erste Glas, und 0 für alle weiteren Gläser.
Die Zahlungsbereitsschaft von Maria sind 32 für das
erste Glas, 20 für das zweite Glas, 15 für das dritte
Glas, und 0 für alle weiteren Gläser. Nehmen Sie an,
daß bei Indifferenz sowohl Eva als auch Maria stets
möglichst viel kaufen. Ferner kaufen Eva und Maria Himbeerbrause ausschließlich bei Anna, die Himbeerbrause zu Grenzkosten von Null herstellen kann
und risikoneutral ist. Anna kennt auch die Nachfragen von Eva und Maria kann aber die beiden Zwillinge nicht unterscheiden. Die Wahrscheinlichkeit, daß
entweder Eva oder Maria Kundin ist, ist jeweils 12 .
• Wenn Anna einen festen Preis für jedes Glas
Himbeerbrause verlangt, macht sie den größten
Gewinn mit einem Preis von etwa. . . (11 Punkte)
b
c
d
e
15
20
25
32
11: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
3
1
4
40
15
3
1
4
60
20
2
0
2
40
25
1
0
1
25
32
1
0
1
32
Der Einfachheit halber berechnen wir den Gewinn
aus zwei Verkäufen. Wir sehen, daß der Gewinn
bei einem Preis vom 15 am höchsten ist.
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, daß sie aber
unterschiedliche Preise für das erste, zweite und
dritte Glas, das ein Zwilling kauft, verlangen
kann. In diesem Fall wird sie für das erste Glas
den folgenden Preis verlangen. . .
(7 Punkte)
b
c
d
e
20
25
32
15
12: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
1
1
2
20
15
1
1
2
30
20
1
0
1
20
25
1
0
1
25
32
1
0
1
32
Der Gewinn ist also bei einem Preis vom 32 am
höchsten.
• . . . und für das zweite Glas. . .
b
c
25
32
13: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
15
20
1
0
1
20
(7 Punkte)
e
20
25
0
0
0
0
32
0
0
0
0
Der Gewinn ist also bei einem Preis vom 20 am
höchsten.
• . . . und für das dritte Glas. . .
b
c
32
15
14: a 10
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
10
1
0
1
10
d
15
1
0
1
15
20
20
0
0
0
0
25
0
0
0
0
32
0
0
0
0
• Nehmen Sie nun an, daß Anna die beiden Zwillinge nicht unterscheiden kann, und auch nicht
unterschiedliche Preise für das erste, zweite und
dritte Glas, das eine Kundin kauft, verlangen
kann. Sie kann aber unterschiedliche Güterbündel
anbieten. Jede Kundin kann zu den angegebenen
Preisen beliebig viele Güterbündel kaufen. Geben
Sie alle Güterbündel an, die Anna im Gewinnmaximum anbieten kann (mehrere Antworten
möglich):
(45 Punkte)
1 Glas zum Preis von 15
1 Glas zum Preis von 20
2 Gläser zum Preis von 52
3 Gläser zum Preis von 32
3 Gläser zum Preis von 67
Nehmen wir zunächst an, Anna würde jeweils nur
1
15
3
1
4
45
Menge
Preis
Konsum Maria
Konsum Eva
Konsum gesamt
2× Gewinn
1
20
2
0
2
40
2
52
1
0
1
52
3
32
1
0
1
32
3
67
1
0
1
67
Der Gewinn ist also bei 3 Gläsern zum Preis
von 67 am höchsten. Die Zahlungsbereitschaft von
Maria wird vollständig abgeschöpft. Wir sehen
aber, daß Anna auch noch das Bündel 2 Gläser
”
zum Preis von 52“ anbieten kann. Auch hier wird
die Zahlungsbereitschaft von Maria vollständig
abgeschöpft, sie ist also indifferent, und kauft deshalb annahmegemäß das Bündel zum Preis von
67.
Aufgabe:
Betrachten Sie das folgende Spiel (Auszahlungen von Spieler 1 stehen links unten, Auszahlungen von Spieler 2 stehen rechts oben):
l
t
Spieler
1
(7 Punkte)
e
25
Der Gewinn ist also bei einem Preis vom 15 am
höchsten.
15a:
15b:
15c:
15d:
15e:
ein Güterbündel anbieten:
m
b
8
5
4
Spieler 2
c
3
1
2
1
5
7
2
3
0
r
2
1
0
4
2
t
m
Spieler2
c
l
1
3
2
8
5
1
7
5
finden wir die beiden obigen Gleichgewichte. (5, 1)
und (8, 3) sind keine Notation für Gleichgewichte.
• Im gemischten Gleichgewicht werden die Strategien mit folgenden Wahrscheinlichkeiten gespielt
(mehrere Antworten möglich)
(60 Punkte)
17a:
17b:
17c:
17d:
(l, c, r) mit ( 58 , 38 , 0)
(t, m, b) mit ( 23 , 13 , 0)
(t, m, b) mit ( 14 , 34 , 0)
(t, m, b) mit ( 23 , 0, 13 )
πm =
3
8
·7+
5
8
·5 =
46
.
8
Spieler 2 wird durch (t, m, b) mit ( 23 , 13 , 0) indifferent zwischen c und l:
πc = 23 · 1 + 13 · 5 = 73
πl = 23 · 3 + 13 · 1 = 73
Diese beiden gemischen Strategien bilden also ein
Gleichgewicht.
Die gemischte Strategie (t, m, b) mit ( 14 , 34 , 0)
macht Spieler 2 nicht indifferent, er wird immer
c spielen, dann aber wird Spieler 1 nicht mehr
mischen wollen.
Aufgabe:
A verkauft eine Einheit eines unteilbaren Gutes an B. A weiß, dass B eine Zahlungsbereitsschaft von 3 hat. Der Preis bestimmt sich über
folgendes Spiel: Zuerst schlägt A dem B einen Preis
p ∈ vor. Wenn dann B annimmt, hat A den Nutzen p und B hat den Nutzen 3 − p. Wenn B nicht
annimmt, haben beide einen Nutzen von 0.
Welche der folgenden Aussagen sind wahr (mehrere
Antworten möglich):
(65 Punkte)
Das Spiel ist sequentiell, d.h. wir verwenden
Rückwärtsinduktion. Für jede Strategie von A muß
B eine beste Antwort spielen, gegeben diese Strategie
von B muß dann auch A eine beste Antwort spielen.
A wählt p = 3, B nimmt nur an, wenn p ≤ 3 ist ein
Gleichgewicht. Beide können sich durch abweichen
nur verschlechtern.
A wählt p = 32 B nimmt nur an, wenn p ≤ 32 ist kein
Gleichgewicht. In allen Fällen, in denen A einen
Preis p ∈ ( 32 , 3) wählt, spielt B keine beste Antwort.
A wählt p = 0, B nimmt nur an, wenn p ≤ 0 ist kein
Gleichgewicht, In allen Fällen, in denen A einen
Preis p ∈ (0, 3) wählt, spielt B keine beste Antwort.
A wählt p = 3, B nimmt nur an, wenn p < 3 ist
kein Gleichgewicht, A kann sich durch einen kleineren Preis verbessern.
A wählt p = 3, B nimmt nur an, wenn p ≤ 7 ist
kein Gleichgewicht, A kann sich durch einen höheren Preis verbessern.
Aufgabe:
Drei Schakale befinden sich vor einem
Beutetier. Wenn Schakal 1 das Tier nicht frisst, endet das Spiel. Wenn Schakal 1 die Beute frisst, kann
Schakal 2 sich entscheiden, ob er den Schakal 1 frisst.
Wenn nicht, endet das Spiel. Wenn ja, kann sich
Schakal 3 entscheiden, ob er den Schakal 2 frisst oder
nicht. Die Auszahlungen bemessen sich für jedes Tier
nach folgender Tabelle:
2
• Bitte markieren Sie alle Gleichgewichte in reinen
Strategien (mehrere Antworten möglich, achten
Sie auf die richtige Schreibweise):
(40 Punkte)
16: a (5, 1) b (m, c) c (t, l) d (t, r) e (8, 3)
Spieler 1 wird nie b spielen, da diese Strategie
durch m strikt dominiert wird. Dann wird aber
Spieler 2 nie r spielen, da diese Strategie durch l
dominiert ist. In dem verbleibenden Spiel
Spieler1
17e: (l, c, r) mit (0, 38 , 58 )
Wir haben oben bereits gesehen, daß b und r nie
gespielt werden. Damit fallen bereits 2 der fünf
Möglichkeiten fort. Durch (l, c, r) mit ( 58 , 38 , 0)
wird Spieler 1 indifferent zwischen t und m:
πt = 38 · 2 + 58 · 8 = 46
8
18a: Wenn A einen Preis p = 3 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18b: Wenn A einen Preis p = 0 vorschlägt, ist es
eine beste Antwort von B anzunehmen
18c: Wenn A einen Preis p = 3 vorschlägt, ist es
eine beste Antwort von B nicht anzunehmen
18d: Wenn A einen Preis p = 3 vorschlägt, hat B
keine beste Antwort
18e: Wenn A einen Preis p = 32 vorschlägt, ist es
eine beste Antwort von B anzunehmen
Wenn A einen Preis p = 3 vorschlägt hat B einen
Nutzen von 0, egal ob er annimmt oder ablehnt. Beides ist also eine beste Antwort. Wenn A einen Preis
p = 32 vorschlägt, bekommt B nichts wenn er ablehnt, aber 32 wenn er annimmt, also ist es beste
Antwort anzunehmen. Wenn A einen Preis p = 0
vorschlägt, bekommt B nichts wenn er ablehnt, aber
3 wenn er annimmt, also ist es beste Antwort anzunehmen.
Ein Gleichgewicht dieses Spiels ist (mehrere Antworten möglich):
(65 Punkte)
19a:
19b:
19c:
19d:
19e:
A
A
A
A
A
wählt
wählt
wählt
wählt
wählt
p=
p=
p=
p=
p=
0, B nimmt nur an, wenn p ≤ 0
3
, B nimmt nur an, wenn p ≤ 32
2
3, B nimmt nur an, wenn p < 3
3, B nimmt nur an, wenn p ≤ 3
3, B nimmt nur an, wenn p ≤ 7
fressen
nicht fressen
gefressen
werden
1
1
nicht gefressen werden
3
2
Welche der folgenden Aussagen gelten im Gleichgewicht (mehrere Antworten möglich):
(50 Punkte)
20a: Schakal 1 wird immer fressen
20b: Schakal 3 wird immer fressen, wenn er zum
Zug kommt
20c: Schakal 3 bekommt mehr als die anderen
20d: Schakal 1 bekommt mehr als die anderen
20e: Schakal 2 wird immer fressen, wenn er zum
Zug kommt
Wir lösen das Spiel durch Rückwärtsinduktion.
Nach Schakal 3 gibt es keinen weiteren Zug. Schakal
3 stellt sich besser wenn er frisst, also wird er immer
fressen. Vor Schakal 3 kommt Schakal 2 zum Zug.
Er weiß nun, daß er immer gefressen wird, sollte er
selber fressen. Also wird er sich für nicht fressen“
”
entscheiden, und das Spiel enden lassen. Vor Schakal 2 kommt Schakal 1 zum Zug. Er weiß nun, daß
Schakal 2 nie fressen wird, er bekommt also eine
höhere Auszahlung, wenn er frißt.
maximal erreichbare Punktzahl: 587
davon durch Randomisieren erreichbar: 259.9