Handout Uebung 1

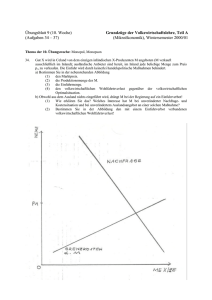
Übung zu Mikro II (WS 04/05)
Tri Vi Dang
Handout zu Übung 1
Vorbemerkung:
Hinweise auf Fehler sind willkommen.
Keine Gewähr für die vollständige Richtigkeit der Ausführungen.
Aufgabe (ai)
Diskutieren Sie den Zusammenhang zwischen dem Grenznutzen eines Gutes für einen
Konsumenten und dessen Nachfrage nach dem Gut.
Frage 1
Was versteht man unter den Grenznutzen eines Gutes X?
Antwort 1
Frage 2
Ist die Annahme von abnehmenden Grenznutzen plausibel und was ist die ökonomische
Intuition?
Antwort 2
1
U
U(x)
“U’(1)“
“U’(0)“
Menge
Frage 3
Was ist der Zusammenhang zwischen Grenznutzen und Zahlungsbereitschaft?
Antwort 3
Hamburger-Beispiel
Preis, U’
p
2
1.75
1.5
D=MB
1
2
3
Menge
Bemerkung:
In Aufgabe 2d auf Blatt 2 wird eine fallende Nachfragekurve formal hergeleitet.
2
Q
Frage 4
Warum nimmt man stetige Nutzenfunktionen an, obwohl Güter nicht beliebig teilbar sind?
Antwort 4
Aufgabe (aii)
Diskutieren Sie den Zusammenhang zwischen Grenzkosten eines Gutes für den
Produzenten und dessen Angebot von dem Gut.
Frage 5
Was ist der Zusammenhang zwischen Grenzkosten und individueller Angebotskurve?
Antwort 5
Beispiel für steigende MC (Pizza Herstellung innerhalb 10 Minuten)
Preis
p
S=MC
8
7
6
1
2
3
Menge
3
Q
Eine blöde story:
Bemerkung:
In Aufgabe 3d auf Blatt 2 wird eine steigende Angebotskurve formal hergeleitet.
Aufgabe (aii)
Diskutieren Sie den Zusammenhang zwischen individueller Nachfrage und
Marktnachfrage
Lit: PR 4.3 (S.117f.)
Frage 6
Wie kommt man von den individuellen Nachfragefunktionen zur Marktnachfrage?
Antwort 6
Q1
Q2
QM
10
190
70
260
P
20
180
60
240
30
170
50
220
4
Aufgabe (aiv)
Diskutieren Sie den Zusammenhang zwischen individuellem Angebot und
Marktangebot.
Lit: PR 8.6 (S.207f.)
Frage 7
Wie kommt man von den individuellen Angebotsfunktionen zum Marktangebot?
Antwort 7
10
40
40
80
Q1
Q2
QM
P
20
50
50
100
30
100
60
160
Aufgabe (bi)
Frage 8
Auf welche Annahmen basiert das Konstrukt “vollkommener Wettbewerb“?
Lit: PR 8.1 (S.252f.)
Antwort 8
Basic Annahmen dieses "Konstrukt"
- viele Anbieter und Nachfrager.
- Einzelne Konsumenten und Produzenten sind "klein" relativ zum Gesamtmarkt
- Sie haben keinen Einfluß auf Marktpreis
- Betrachten Marktpreis als exogene Größe
- Konsumenten und Produzenten können zum Marktpreis beliebig viel kaufen bzw,,
verkaufen.
5
Alle Firmen auf diesem Markt produzieren das gleiche Gut (keinerlei Unterschiede in
Qualität, Funktionalität, usw.)
Aufgabe (bii)
Frage 9
Wie ist ein Markt-GG definiert?
Antwort 9
Frage 10
Wie bestimmt man ein Markt-Gleichgewicht?
Antwort 10
Hier : D(Q)=P=280−2Q und S(Q)=P=40+4Q
40+4Q =280−2Q
Æ
Q*= 40
Æ
P*=40+4*40= 200
6
Graphische Darstellung
Preis
280
S
P*
40
D
Menge
Q*
140
Aufgabe (biii)
Frage 11
Warum kann man p* und Q* als GG-Preis und GG-Menge interpretieren?
Lit: PR 2.2 (S.23f.)
Antwort 11
Verbale Argumentation
Fall 1: p>p*
Fall2 p<p*
Preis
p
S
S
p
p
D
QD <
QS
D
Menge
Überangebot
Produzenten unterbieten sich
Preise fallen
Weniger Produktion
Mehr Nachfrage
QS <
QD
Q
Übernachfrage
Konsumenten überbieten sich
Preis steigt
Mehr Produktion
Weniger Nachfrage
7
Aufgabe (biv)
Berechnen und Interpretieren Sie die Konsumenten-, und Produzentenrente sowie
die soziale Wohlfahrt.
Lit: 4.4 (S. 123f.)
Frage 12
Was besagt die Konsumentenrente?
Antwort 12
Preis, MB
2
1.75
1.5
1
p
1
2
3
Menge
Rente der 1. Einheit= ZB−p=2−1=1
Rente der 2. Einheit=ZB−p=1.75−1
Rente der 3. Einheit=ZB−p=1.5−1
Rente=2.25
8
Preis
280
KS
S
240
40
D
Menge
Q*
140
Frage 13
Wie berechnet man die Konsumentenrente?
Antwort 13
Hier:
Q*
40
KS = ∫ (280 − 2Q − p * )dQ = ∫ (280 − 2Q −200)dQ
*
0
= [80Q − Q ² ] = 1600
0
40
0
Frage 14
Was ist die Produzentenrente und wie berechnet man sie?
Antwort 14
Lit: PR 8.6 (S.266f.)
9
Preis
280
PS
S
240
40
D
Menge
140
Produzent B
Produzent B ist bereit, für 200 Euro das Gut zu verkaufen, bekommt aber 240 Euro. Er hat
somit einen "Gewinn" von 40 Euro. (Gewinn=Produzentenrente−Fixkosten)
Hier
40
PS = ∫ (200 − 40 − 4Q)dQ = [160Q − 2Q ² ]0 = 3200
40
*
0
Frage 15
Wie ist die soziale Wohlfahrt definiert und wie hoch ist sie in dem Beispiel?
Antwort 15
TBC=CSC+PSC=4800
10
Aufgabe (ci)
Frage 16
Auf welche Annahmen basiert das Konstrukt “Monopol“?
Antwort 16
Lit: PR 10.1 (S.328f.)
Aufgabe (cii)
Frage 17
Welche Menge maximiert den Gewinn des Monopolisten?
Antwort 17
Allgemeiner Ansatz
Monopolist löst folgendes Maximierungsproblem
Hier: p=280−2Q
MC=40+4Q
C=(Stammfunktion von MC)=40Q+2Q²
π (Q) = (280 − 2Q) ⋅ Q − C (Q)
π (Q) = (280 − 2Q) ⋅ Q − (40Q + 2Q ²)
dπ (Q)
= 280 − 4Q − (40 + 4Q) = 0
dQ
⇔
280 − 4Q − 40 − 4Q = 0
1
424
3 1
424
3
MR
⇔
(Optimum: MR=MC)
MC
240 − 8Q = 0
11
⇒
QM=30
PM=280−2QM=220
Alternative Rechnung bei linearer Nachfrage
Aufgabe (ciii)
Vergleichen Sie Preis, Menge, Konsumenten- und Produzentenrente sowie soziale
Wohlfahrt mit den Werten aus (b).
Frage 18
Wie verändern sich KS, PS und Wohlfahrt (total benefit)?
Antwort 18
30
KS M = ∫ (280 − 2Q −220)dQ = [60Q − Q ² ]0 = 900 < KS *
30
0
30
PS M = ∫ (220 − 40 − 4Q)dQ = [180Q − 2Q ² ]0 = 3600 > PS *
30
0
TBM=CSM+PSM=4500< TB*=4800
Definition:
Wohlfahrtsverlust (Dead weight loss, DWL)= TB* − TBM
DWL = 300
12
Graphische Darstellung
Preis
MC
PM
DWL
MR
QM
D
Menge
Preis
KS
MC
PM
MR
QM
D
Menge
Preis
PS
MC
PM
MR
M
Q
D
Menge
Aufgabe (civ)
Frage 19
Gelten generell QM< Q* , PM>P*, KS* < CSC , PSM > PS* und TBM < TB*?
Antwort 19
13
Preis
S=MC
MR
D
Menge
Aufgabe (di)
Nun wird angenommen, daß bei der Produktion Stoffe freigesetzt werden, die zu
Umweltschäden führen und das Wohlbefinden der Gemeinschaft beeinträchtigen. Der
(Grenz-) Schaden wird durch folgende Funktion beschrieben: MD=2Q.
Frage 20
Wie hoch ist die soziale (Netto-)Wohlfahrt unter vollkommenem Wettbewerb?
Antwort 20
Hier:
TD(QC) =40²=1600
NBC=TBC-TDC=4800-1600=3200
14
Preis
MC
MD
D
Menge
Aufgabe (di)
Frage 21
Wie hoch ist die soziale (Netto-)Wohlfahrt beim Monopol?
Antwort 21
NBM=TBM-TDM=4500-900=3600
Aufgabe (diii)
Frage 22
Welche Menge maximiert die soziale (Netto-)Wohlfahrt und wie hoch ist die soziale Netto
Wohlfahrt ?
Antwort 22
<=> 280−2Q=40+4Q+2Q
<=> Q*= 30
NBM=TBM-TDM=4500-900=3600
15
Alternative Rechnung
[ ]
NB = [280Q − Q² − pQ ]0 + [pQ − 40Q − 2Q ² ]0 − Q ²
x
x
x
0
= 280x − x² − px + px − 40x − 2 x ² − x ²
= 240x − 4x²
dNB
= 240 − 8x = 0
dx
Optimale Menge x=30.
Aufgabe (div)
Frage 23
Ist es immer der Fall, daß ein Monopolist die optimale Menge produziert, wenn es bei der
Produktion zu schädlichen Emissionen kommt ?
Antwort 23
Beispiel: MD=4Q
Æ 280−2Q=40+4Q+4Q
<=> Q*= 24
Sozial optimale Menge Q*=24, Monopol produziert Q=30.
Allgemeines Problem bei sog. Externalitäten ist, daß Firmen diese nicht in ihre Optimierung
berücksichtigen, weil sie die sozialen Kosten nicht tragen müssen.
Aber richtig ist, daß der Monopolist im allgemeinen weniger produziert und somit bei der
Produktion weniger Schadstoffe emittiert.
16
Aufgabe (e)
Die Regierung möchte der Umweltverschmutzung entgegenwirken und plant, eine
Mengensteuer t einzuführen, d.h. auf jede verkaufte Einheit muß der Produzent eine Steuer
von t bezahlen.
Frage 24
Wie hoch muß die Steuer sein, damit die sozial optimale Menge als Gleichgewicht in dem
Markt mit vollkommenen Wettbewerb sich etabliert ?
Antwort 24
280−2Q=40+4Q+t
<=>240=6Q+t
Für Q=30: 240=(6+t)30 Æ t=60
Unternehmen internalisiert die Umweltkosten bei der Produktion.
17