Vorlesungsbegleitende Unterlagen zur Vorlesung BWL I

Vorlesungsbegleitende Unterlagen
zur Vorlesung BWL I — Teil A
von Prof. Dr. Matthias Sander
Christoph Safferling
Wintersemester 2000/2001
Inhaltsverzeichnis
1 Gegenstand der Betriebswirtschaftslehre
1.1 Der Erfahrungsgegenstand der BWL . . . . . . . . . . .
1.1.1 Der Begriff des Betriebs . . . . . . . . . . . . . .
1.1.2 Arten von Betrieben . . . . . . . . . . . . . . . .
1.2 Der Erkenntnisgegenstand der BWL . . . . . . . . . . .
1.2.1 Der Begriff des Wirtschaftens . . . . . . . . . . .
1.2.2 Das Ökonomische Prinzip . . . . . . . . . . . . .
1.3 Betriebliche Leistungs- und Finanzprozesse im Überblick
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
3
3
4
4
4
4
2 Beschaffung und Lagerhaltung
2.1 Begriffliche Grundlagen . . . . . . . . . . . . . . . . . . .
2.1.1 Definitionen . . . . . . . . . . . . . . . . . . . . . .
2.1.2 Arten von Verbrauchsfaktoren . . . . . . . . . . .
2.1.3 Vertragsmäßige Materialbeschaffung . . . . . . . .
2.1.4 Physische Materialbeschaffung . . . . . . . . . . .
2.2 Ziele der Materialwirtschaft . . . . . . . . . . . . . . . . .
2.3 Materialbedarfsplanung . . . . . . . . . . . . . . . . . . .
2.3.1 Programmgebundene Materialbedarfsplanung . . .
2.3.2 Verbrauchsgebundene Materialbedarfsplanung . . .
2.3.3 Materialklassifizierung mit Hilfe der ABC–Analyse
2.4 Lagerplanung . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Lagerarten und Lagerfunktionen . . . . . . . . . .
2.4.2 Lagerhaltung und Organisation der Beschaffung .
2.4.3 Langfristige Lagerkapazitätsplanung . . . . . . . .
2.4.4 Kurzfristige Bestellplanung . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
5
5
6
7
7
8
8
9
10
11
11
11
12
12
3 Produktion
3.1 Grundlagen der Produktionstheorie . . . . . . .
3.2 Produktionsfaktoren . . . . . . . . . . . . . . .
3.3 Produktionsfunktionen . . . . . . . . . . . . . .
3.3.1 Produktionsfunktion vom Typ A . . . .
3.3.2 Die Cobb–Douglas Produktionsfunktion
3.3.3 Leontieff Produktionsfunktionen . . . .
3.3.4 Produktionsfunktion vom Typ B . . . .
3.4 Grundlagen der Kostentheorie . . . . . . . . . .
3.4.1 Kostenfunktionen . . . . . . . . . . . . .
3.4.2 Minimalkostenkombination . . . . . . .
3.4.3 Kostenfunktion für den Typ B . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
14
14
14
14
15
18
19
19
21
22
23
25
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Absatz
4.1 Einführung . . . . . . . . . . . . . . . . . . . . .
4.1.1 Marketingziele . . . . . . . . . . . . . . .
4.1.2 Marketinginstrumente . . . . . . . . . . .
4.2 Produkt- und Sortimentspolitik . . . . . . . . . .
4.2.1 Produktinnovation . . . . . . . . . . . . .
4.2.2 Produktvariation . . . . . . . . . . . . . .
4.2.3 Produktdifferenzierung . . . . . . . . . . .
4.2.4 Produkteliminierung . . . . . . . . . . . .
4.2.5 Sortimentsplanung . . . . . . . . . . . . .
4.3 Kontrahierungspolitik . . . . . . . . . . . . . . .
4.3.1 Grundlagen der Preispolitik . . . . . . . .
4.3.2 Ansätze der Preistheorie . . . . . . . . . .
4.3.3 Praxisorientierte Ansätze der Preisfindung
4.4 Kommunikationspolitik . . . . . . . . . . . . . .
4.4.1 Ziele der Kommunikationspolitik . . . . .
4.4.2 Werbung . . . . . . . . . . . . . . . . . .
4.5 Distributionspolitik . . . . . . . . . . . . . . . . .
4.5.1 Grundlagen . . . . . . . . . . . . . . . . .
4.5.2 Absatzwegewahl . . . . . . . . . . . . . .
4.5.3 Absatzmittlerwahl . . . . . . . . . . . . .
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
28
28
28
28
29
30
32
33
33
34
34
34
36
38
39
39
39
41
41
41
42
Kapitel 1
Gegenstand der
Betriebswirtschaftslehre
Die BWL ist eine Realwissenschaft. Sie behandelt überwiegend wirtschaftliche,
aber auch technische, religiöse, rechtliche, kulturelle und weitere Sachverhalte.
Das Objekt der Untersuchung (der Begierde) ist ein Betrieb.
1.1
Der Erfahrungsgegenstand der BWL
1.1.1
Der Begriff des Betriebs
Betrieb:
Eine technische, soziale und wirtschaftliche Einheit mit
der Aufgabe der Bedarfsdeckung mit selbstständigen
Entscheidungen und eigenen Risken. (Kosiol, 1962)
Wird der Eigenbedarf gedeckt, so spricht man von Haushalten, wird er
Fremdbedarf gedeckt, so ist von einem Unternehmen die Rede. Betrieb wird
hier als Oberbegriff verwendet.
1.1.2
Arten von Betrieben
ˆ Private Unternehmen verfolgen privatwirtschaftliche Ziele. Unter diesen
sind die des Umsatz- oder der Gewinnmaximierung am prominentesten.
ˆ Öffentliche Unternehmen verfolgen gemeinwirtschaftliche Ziele. Als Beispiele können z.B. Verlustminimierung oder Absatzmaximierung dienen.
ˆ Private Haushalte: hier wird zwischen ursprünglichen und abgeleiteten
Haushalten differenziert.
– Ursprüngliche Haushalte sind das, was man sich unter den Haushalten vorstellt: Familien, Einpersonenhaushalte usw.
– Abgeleitete Haushalte sind Haushalte im weiteren Sinne: Vereine,
Verbände oder Gesellschaften bürgerlichen Rechts
ˆ Öffentliche Haushalte können in Form von Körperschaften sowie Anstalten
oder öffentlich-rechtliche Stiftungen auftreten.
3
Weiterhin wird zwischen Sachleistungs- und Dienstleistungsunternehmen unterschieden.
1.2
Der Erkenntnisgegenstand der BWL
Erkenntnisgegenstand der BWL ist das wirtschaften in Betrieben und der optimaler Einsatz knapper Güter in denselben.
1.2.1
Der Begriff des Wirtschaftens
Wirtschaften ist der Entscheiden über die Verwendung von knappen Gütern in
Betrieben.
Auf Gewinnmaximierung wird sich dabei nicht konzentriert, da dieses als
Erkenntnisgegenstand nicht ausreicht.
1.2.2
Das Ökonomische Prinzip
Ausgangspunkt ist das
Rationalprinzip
gemilderte Form:
der zielbezogene Einsatz der knappen Güter
strenge Form:
optimale Ausbringung bei gegebenen knappen
Gütern
oder: gegebene Ziele sollen mit minimalen Einsatz der knappen Güter erreicht werden
Ergiebigkeitsprinzip
(ökonomisches Prinzip i. w. S.)
wirtschftliche Ergiebigkeit
(ökonomisches Prinzip i. e. S.)
soziale
Ergiebigkeit
wertmäßig
(Ökonomizität)
mengenmäßig
(Technizität)
Absolut
(Gewinn)
Relativ
(Rentabilität)
1.3
materielle
Ergiebigkeit
ökologische
Ergiebigkeit
Betriebliche Leistungs- und Finanzprozesse
im Überblick
Bei der Wertschöpfung im Unternehmen (Value Added) spricht man vom Umsatz minus den Vorleistungen. Die betriebliche Wertschöpfung ist Teil der gesamtwirtschaftlichen Wertschöpfung, dem Bruttoinlandsprodukt (BIP).
Die Wertschöpfungskette im Unternehmen sieht stark vereinfacht wie folgt
aus:
Beschaffung → Produktion → Absatz
4
Kapitel 2
Beschaffung und
Lagerhaltung
2.1
Begriffliche Grundlagen
2.1.1
Definitionen
Kleine Vokabelstunde für BWLer:
ˆ Beschaffung i. w. S.: Die Versorgung des Unternehmens mit Produktionsfaktoren (Kapital, Informationen, Material, Personal etc.)
ˆ Beschaffung i. e. S.: Die Versorgung des Unternehmens mit Verbrauchsfaktoren
2.1.2
Arten von Verbrauchsfaktoren
ˆ Betriebsmittel: Anlagen mit Nutzungspotential über mehrere Perioden
(keine Verbrauchsfaktoren)
ˆ Verbrauchsfaktoren: Gehen bei einmaliger Nutzung im Wertschöpfungsprozeß unter
ˆ RHB-Stoffe
R: Realgüter, die unmittelbar in die produzierten Güter eingehen und
dessen Hauptbestandteil sind
H: Hilfsgüter, die in die Produktion mit eingehen; sie erfüllen eine Nebenfunktion und sind von untergeordneter Bedeutung
B: Betriebsmittel, die nicht in die Produktin mit eingehen.
ˆ Bezogene Teile (Kaufteile): Halbfertigfabrikate und vorveredelte Produkte
fallen unter diese Kategorie.
ˆ Handelsware: werden verkauft, aber nicht selbst hergestellt oder verändert.
ˆ RH–Stoffe und Halb- sowie Fertigfabrikate werden Werkstoffe genannt.
5
2.1.3
Vertragsmäßige Materialbeschaffung
Unter die vertragsmäßige Materialbeschaffung (Einkauf) fällt die Gestaltung
der Kontrahierungsbeziehungen zu den einzelnen Beschaffungspartnern. Man
unterscheidet zwischen vier verschiedenen Politiken.
Beschaffungsprogrammpolitik
Bei der Beschaffungsprogrammpolitik geht es um die Frage, welche Güter in
welcher Menge in eigener Leistung erstellt werden. Eine Vertikale Integration
benötigt weniger outsourcing1 , hier wird also über Fremd- oder Eigenbezug
entscheiden.
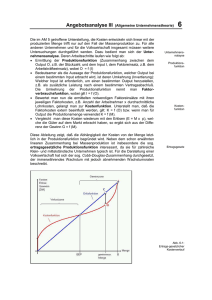
Dazu bedient man sich des Mittels der Break–Even–Analyse. Fremdbezug
hat im Allgemeinen die geringeren Fixkosten, dafür aber höhere variable Kosten.
Daraus läßt sich auf einfache Weise die optimale Menge x∗ feststellen, ab der
sich der Fremdbezug nicht mehr lohnt.
Die Fremdbezugskosten K f und die Eigenherstellungskosten K e müssen sich
im Break-Even-Punkt gleichen.
KFe + KVe (x) = KFf + KVf (x)
⇒ x∗
=
KFf − KFe
KVe − KVf
Beschaffungspartnerpolitik
Bei der Beschaffungspartnerpolitik steht die Auswahl der Lieferanten im Mittelpunkt. Es stellt sich die Frage des Singe-Sourcing oder des Multiple-Sourcing,
d.h. ob ein oder ob mehrere Lieferanten beauftragt werden. Je nach Entscheidung ergeben sich unterschiedliche Vor- und Nachteile bei der Versorgung, den
Konditionen und der Abwicklung.
ein Lieferant
mehrere Lieferanten
langfr. Vertrag
fallweiser Einkauf
Versorgung
–
+
+
–
Konditionen
+
–
–
+
Abwicklung
+
–
+
–
Beschaffungspreis- und konditionenpolitik
Diese Politik ist eng mit der Beschaffungspartnerpolitik verbunden, da bei der
Auswahl der Lieferanten diese Gesichtspunkte meist mit erörtert werden.
Gerne wird die Auswahl mittels eines Scoringverfahrens2 vollführt. Dabei
wird in einer Tabelle den einzelnen Merkmalen Punkten zugeordnet und diese
dann gewichtet. Bei vielen potentiellen Lieferanten kann es sinnvoll sein, zuerst
1 Obwohl
outgesourced“ bereits im Duden steht, sollte man es vielleicht doch lieber ver”
meiden, dieses Wort in der Schriftsprache zu benutzen.
2 Zum Verfahren bei der Scoring Analyse siehe S. 31
6
eine Grobgliederung und Grobauswahl der Lieferanten zu berechnen und erst
danach die Feinunterscheidung vorzunehmen.
So kommt man schließlich zur gewichteten Gesamtpunktzahl (GGPZi ) für
den einzelnen Lieferanten i.
X
GGPZi =
gj · aij
j
Mit gj als der Gewichtung und aij als der Punktzahl für das Kriterium j.
Beschaffungskommunikationspolitik
Die Beschaffungskommunikationspolitik zielt auf die Beeinflußung der Beschaffungspartner vor, während und nach dem Beschaffungsvorgang. Wird sie davor
angewand spricht man von Beschaffungsanbahnung, während des eigentlichen
Vorgangs spricht man von der Verhandlung und danach von der Pflege der Beziehungen.
Der Grund dafür, daß auch nach den Verhandlungen noch Kommunikationspolitik betrieben wird ist der, daß sogenannte Lead Users“ bei einem Lieferan”
ten günstigere Konditionen erzielen können.
2.1.4
Physische Materialbeschaffung
Die physische Materialbeschaffung (Logistik) hat die Aufgabe, die Unternehmensprozesse mit Material zu versorgen.
Logistik:
eine Querschnittsfunktion, deren Aufgabe es ist, die
räumlichen, zeitlichen und mengenmäßigen Differenzen
zwischen Zulieferen (auch: Lager) und Abnehmern zu
überbrücken.
→ Logistische Funktion
Es existieren verschiedene Funktionen der Lagerung, des Transports, der
Materialhandhabung- und verpackung. In dieser Vorlesung beschränken wir uns
auf die Lagerung und auch hier lassen wir den wichtigen strategischen Aspekt
der Standortplanung aus. Vielmehr wenden wir uns dem operativen Aspekt der
Bestellmengen und der Zeitpunkte der Bestelung zu.
2.2
Ziele der Materialwirtschaft
Die Ziele lassen sich in generelle Ziele und Einzelkriterien aufspalten. Generelle
Ziele beinhalten die
ˆ Technische Komponente: die Bereitstellung einer bestimmten Menge und
Qualität eines Produkts zur richtigen Zeit am richtigen Ort
ˆ Ökonomische Komponente: hier gelten übergeordnete ökonomische Ziele,
wie z.B. die Gewinnmaximierung
Außerdem werden noch die Einzelkriterien berücksichtigt:
ˆ Produktqualität
7
ˆ Zeit, Ort, Quantität
ˆ Kosten
ˆ Flexibilität (Just–in–Time Production)
2.3
Materialbedarfsplanung
2.3.1
Programmgebundene Materialbedarfsplanung
Zur Ermittlung des Gesamtbedarfs bei der programmgebundenen Materialbedarfsplanung geht man in folgenden Schritten vor:
1. Die Primärbedarfsmenge Yi i = 1, . . . , n wird als unabhängiger, exogen
gegebener Bedarf ermittelt. Sie ergibt sich aus der Absatz- bzw. Vorratsplanung.
2. Zur Erstellung von Yi sind bestimmte Rohstoffe, Teile und/oder Baugruppen notwendig:
aij bzw. A = (aij )
aij bezeichnet die Menge eines Guts i, das unmittelbar zur Herstellung
einer Einheit des Guts j benötigt wird. Es ergibt sich so der Input- oder
Direktbedarfskoeffizient.
3. Gesucht sind die Gütermengen Si , die benötigt werden um Yi herzustellen.
Si = Sekundärbedarf =
n
X
aij xj
∀i
j=1
Es gilt: Gesamtbedarf = Primärbedarf + Sekundärbedarf
Xi
= Yi + Si
n
X
= Yi +
aij xj
j=1
4. Alternativ ist es auch möglich den Gesamtbedarf in der Vektorschreibweise
zu ermitteln. ~x = (x1 , . . . , xn ) ~y = (y1 , . . . , yn )
~x = ~y + A · ~x bzw.
~y = (E − A) · ~x
Mit E als der Einheitsmatrix, A wie oben. Es folgt sofort:
~x = (E − A)−1 · ~y
= G · ~y
G stellt hier die gesuchte Gesamtbedarfsmatrix dar.
Wie bei allen mathematischen Annäherungen in den Wirtschaftswissenschaften ist auch diese mit Problemen behaftet. Folgende Probleme können auftreten:
8
1. Existiert eine eindeutige Lösung des linearen Gleichungssystems
Xi = Yi +
n
X
aij xj
?
j=1
2. Falls eine Lösung existiert, sind alle Gesamtbedarfsmengen > 0 ?
Falls gilt: G = (E − A)−1 ≥ 0, so sind die Probleme nicht existent. Dieses
ist bei Zyklenfreiheit immer gewährleistet.
Ein Gozintograph ist ein häufig verwendetes Hilfsmittel, um die innerbetrieblich verworrenen Produktionsfaktorenbedarfe zu visualisieren. Hierbei
werden die End- und Zwischenprodukte in produktionstechnisch hintereinander folgenden Reihenfolge gebracht und durch Pfeile werden die Betriebswege
dargestellt. Der praktische Nutzen sei dahingestellt.
2.3.2
Verbrauchsgebundene Materialbedarfsplanung
Bei der verbrauchsgebundenen Materialplanung wird aus Daten vergangender
Perioden der jetzige Verbrauch geschätzt. Neben den bekannten statistischen
Möglichkeiten wie etwa das arithmetrische Mittel oder der gewogene, gewichtete
Durchschnitt sind noch weitere Verfahren von Interesse, um die wir uns hier
kümmern werden.
Die Exponentielle Glättung
Hierbei wird der Verbrauch der Vorperiode VT geglättet“ um den Prognose”
fehler der Vorperiode, multipliziert mit einem Glättungsfaktor a. ∗ -Werte sind
in diesem Fall Prognosewerte.
VT∗ = VT∗−1 + a (VT −1 − VT∗−1 )
{z
}
|
Prognosefehler
Je größer a, desto stärker werden jüngere Daten gewichtet.
Güte des Prognosefehlers
Die Güte des Prognosefehlers ist eine wichtige Größe, um das Verfahren beurteilen zu können. Sie berechnet sich durch die Mittlere Absolute Abweichung
(MAA):
MAA =
n
1 X Vt − Vt∗ n t=1
Alle drei Verfahren (Arithmetrisches Mittel, gewogener, gewichteter Durchschnitt und die Exponentielle Glättung) können aber offensichtlich nicht bei
einem trendförmigen Verlauf der Daten benutzt werden (permanent steigende
Daten), da sie den Bedarf so permanenten unterschätzen würden. Im diesem
Falle muß man zum Modell der Einfachen Linearen Regression übergehen.
9
Einfache Lineare Regression
Bei der Linearen Einfachregression3 wird die Summe der quadratischen Abweichungen zwischen den tatsächlichen Verbrauchswerten und der per Regressionsgraden geschätzten Verbrauchswerten minimiert. Als Basis dient das lineare
Schätzmodell Vt∗ = α̂ + β̂ · t.
X
X
X
e2t =
(Vt − Vt∗ )2 =
(Vt − α̂ − β̂ · t)2 → min!
Ableiten nach α̂ und β̂ sowie Nullsetzen ergiebt die notwendige Bedingung
für ein Minimum als
α̂
β̂
= V̄ − β̂ · t
=
=
1
n
und
P
t · Vt − V̄ · t̄
P 2
1
t − t̄2
n
X t · Vt − V̄ − t̄
t2 − t̄2
P
P
mit V̄ = n1
Vt und t̄ = n1
t.
Aber auch dieses Modell löst nicht das Grundproblem der verbrauchsorientierten Materialbedarfsschätzung: es werden Vergangenheitswerte extrapoliert,
ohne die Ursachen der Schwankungen zu berücksichtigen. Genausowenig werden
zukünftige Entwicklungen nicht berücksichtigt. Diese Modelle sind nur adequat
bei Konstanz der Rahmenbedingungen.
2.3.3
Materialklassifizierung mit Hilfe der ABC–Analyse
Im Allgemeinen gilt, daß die programmbezogene Materialbeschaffung mit höheren Planungskosten verunden ist, dafür aber genauere und zuverlässigere Daten
liefert. Da bei teureren Materialien die Opportunitätskosten der Lagerhaltung
höher sind, lohnt es sich bei diesen eher eine programmbezogene Materialbeschaffung durchzuführen. Um aber entscheiden zu können, welche der Materialien programmbezogen und welche verbrauchsorientiert beschafft werden sollen,
muß man eine Differenzierung der Materialarten vornehmen.
A–Güter
B–Güter
C–Güter
hoher Wertanteil, geringer Mengenanteil
liegen zwischen A und C Gütern
geringer Wertanteil, hoher Mengenanteil
Um die Materialien einordnen zu können geht man folgenderweise vor:
1. Wertmäßiger Periodenverbrauch (Verbrauchsmenge mal Preis pro Einheit)
für jede Materialeinheit ermitteln
2. Wertmäßiger Periodenverbrauch des jeweiligen Materials wird in Verhältnis zum wertmäßigen Gesamtverbrauch gesetzt
3 Man
erinnere sich an die Methode der kleinsten Quadrate in Statistik I!
10
3. Einzelne Materialarten werden in absteigender Reihenfolge hinsichtlich ihres prozentualen Anteils am wertmäßigen Verbrauch sortiert
Eine graphische Darstellung ist in Folie (B-12) der Foliensammlung vom WS
2000/2001 zu finden.
2.4
2.4.1
Lagerplanung
Lagerarten und Lagerfunktionen
ˆ Lagerarten, in Reihenfolge des Produktionsprozesses:
– Eingangslager
– Handlager
– Zwischenlager
– Ausgangslager
ˆ Lagerfunktionen:
– Ausgleichsfunktion: das Lager soll Mengen- und Zeitdifferenzen überbrücken
– Sicherungsfunktion: Überbrückung von Engpässen
– Spekulationsfunktion: Lagerhaltung bei steigenden Preisen
2.4.2
Lagerhaltung und Organisation der Beschaffung
Bei nur geringen Lagerhaltungen steigen die Beschaffungskosten, da häufiger
Güter bestellt werden müssen. Dagegen steigen die Lagerhaltungskosten bei
großer Lagerhaltung. Offensichtlich muß es Modelle geben, die zur optimalen
Beschaffungsmenge und zum optimalen Beschaffungsintervall führen.
Fallweise Beschaffung
Hier wird erst bei einem konkreten Bedarf das benötigte Material beschafft.
Lagerhaltung ist (fast) nicht gegeben, somit auch kaum Lagerhaltungskosten.
Dagegen besteht ein hohes Risiko der Produktionsunterbrechung.
Vorratsbeschaffung
Es werden extensive Vorräte aller benötigten Güter angelegt. Die Lagerkosten
steigen immens, aber das Risiko eines Produktionsausfalls ist, zumindest was
Zulieferengpässe angeht, gleich Null.
Fertigungssynchrone Beschaffung
Bei dieser Art der Materialbeschaffung, in letzter Zeit als Just in Time Prinzip“
”
bekannt geworden, werden nur minimale Lagerbestände aufrecht erhalten. Es
werden langfristige Lieferverträge mit hohen Konventionalstrafen abgeschlossen,
die eine exakte und stetige Einhaltung der Termine und auch der Qualität der
gelieferten Waren garantieren sollen.
11
2.4.3
Langfristige Lagerkapazitätsplanung
Langfristig müssen einige Fragen geklärt werden, um die optimale Lagerkapazität herausfinden zu können.
1. Wie groß soll das Lager sein?
→ Kapazitätsplanung
2. Wo soll das Lager gebaut werden?
→ Standortplanung
→ Minimierung der Transportwege
→ Wie viele Lager?
3. Wie soll das Lager ausgestattet werden?
→ Freilager vs. Gebäudelager
→ Speziallager: Tanks, Silos etc.
→ Bodenlager vs. Regallager
→ Ausstattungs- und Organisationsplanung
2.4.4
Kurzfristige Bestellplanung
Kurzfristig gilt es die zeitliche Abgrenzung zwischen Bedarf und Beschaffung
nicht. Der Gesamtbedarf B kann fast wie am Stück beschafft werden. Es gilt
die Zentrale Formel der Güterwirtschaftlichen BWL4 :
B =m·h
Gesamtbedarf B ist gleich Häufigkeit h der Bestellungen pro Periode mal
der Bestellmenge m.
Die optimale Bestellmenge
Die optimale Bestellmenge wird aus einen Optimierungskalkül errechnet:5
K =B·p+
m·p
KF
·B+
·q
m
2
→ min!
mit p als Preis der Mengeneinheit, KF als Bestellfixe Kosten pro Bestellung,
q = (i + l) als dem Opportunitätskostensatz der Lagerhaltung mit i als Zinskostensatz und l als Lagerkostensatz, m der unbekannten Bestellmenge und B
dem Jahresbedarf.
Als notwendige Bedingung für ein Kostenminimum muß die erste Ableitung
gleich Null gesetzt werden und wir erhalten so:
dK
−B · KF
p·q !
=
+
=0
dm
m2
2
4 Manchmal
frage ich mich wirklich, warum ich diesen Schrott hier überhaupt studiere
= unmittelbare Beschaffungskosten + mittelbare Beschaffungskosten +
Lagerkosten, jeweils pro Jahr
5 Gesamtkosten
12
Oder umgeformt die optimale Bestellmenge als:
s
2B · KF
mopt = +
p·q
Prämissen des Modells
ˆ B unter Sicherheit bekannt
ˆ Kontinuierlicher Lagerverbrauch (wg.
mp
2 )
→ Produktionsgeschwindigkeit gleich
ˆ Beschaffungsgeschwindigkeit ist ∞ groß
ˆ Kein Schwund oder Verderb
ˆ p konstant
ˆ Keine finanziellen Restriktionen
ˆ Zinskosten q = (i + l) konstant
ˆ Keine Lagerraumrestriktionen
ˆ Keine fixen Lagerkosten
ˆ KF unabhängig von m
ˆ Keine Abnahmevorschriften (z.B. Mindestabnahmemengen)
Das Modell in der Praxis
In der Praxis wendet man die Grundgleichung der BWL
B =m·h
entweder als Bestellpunktsystem mit B̄ und m̄ als fixen Werten oder als
Bestellrythmussystem mit B̄ und h̄ als fixen Werten an.
13
Kapitel 3
Produktion
3.1
Grundlagen der Produktionstheorie
Produktion
Erstellung von Leistungen durch Kombination von verschiedenen Einsatzfaktoren.
Aufgaben der Produktionstheorie
1. Erklärung des mengenmäßigen Zusammenhangs zwischen Input und Output
2. Aufzeigen von Einflußgrößen auf den Faktorverbrauch
3.2
Produktionsfaktoren
Produktionsfaktoren nach Gutenberg
Werkstoffe
Arbeits- und
Betriebsmittel
abnutzbar
nicht
abnutzbar
Menschliche
Arbeitskraft
objektbezogen
dispositiv
ˆ Potentialfaktoren (Bestandsfaktoren) sind zu gebrauchte Faktoren. Sie
werden längerfristig gebraucht.
ˆ Repetierfaktoren (Verbrauchsfaktoren) sind zu verbrauchende Faktoren, die bei der Wertschöpfung untergehen.
3.3
Produktionsfunktionen
Eine Produktionsfunktion gibt den mengenmäßigen Zusammenhang zwischen
Einbringungs- (Input) und Ausbringungsmenge (Output) an.
Die Outputmenge x wird mit den Einsatzmengen (r1 , . . . , rn ) der n Produktionsfaktoren hergestellt.
14
Produktionsfunktion für Einproduktunternehmen
x = x(r1 , . . . , rn )
Produktionsfunktion für Mehrproduktunternehmen
(x1 , . . . , xm ) = f (r1 , . . . , rn )
für m Produkte und n Produktionsfaktoren.
Produktionsfkt. bei substitutionalen Faktoreinsatzbedingungen
Zwischen Ausbringungsmenge und Einsatzmenge besteht kein fester Zusammenhang.
ˆ Produktionsfunktion vom Typ A (Das Ertragsgesetz)
ˆ Cobb–Douglas Produktionsfunktion
Es gilt:
ˆ Der Produktionskoeffizient ist variabel
ri
ai =
x
mit ai als Produktionskoeffizient des Faktors i, ri als Einsatzmenge des
Faktors i und x als Outputmenge
Produktionsfkt. bei limitationalen Faktoreinsatzbedingungen
Einsatzmenge von Faktoren steht in einem festen Einsatzverhältnis zur Outputmenge (meist technisch bedingt).
ˆ Leontieff Produktionsfunktion
ˆ Produktionsfunktion vom Typ B
Es gilt:
ˆ Der Produktionskoeffizient ist konstant.
ˆ Periphere Substitution: Produktionsfaktoren gegenseitig ersetzbar, aber
nicht vollständig!
3.3.1
Produktionsfunktion vom Typ A
Die Produktionskunktion vom Typ A (sh. Abb. C–3 der Foliensammlung, auch
Das Ertragsgesetz1 genannt) ist von Turgot im 18. Jahrhundert entwickelt
worden. Als Ausgangspunkt benutzte er das Beispiel einer Arbeit in der Landwirtschaft.
Die Hypothese war, daß man zuerst einen überproportional steigenden Grenzertrag (bis Punkt A) bei Erhöhung der Inputmenge, danach jedoch einen unterproportional steigenden (bis Punkt B und letztendlich doch einen negativen
Grenzertrag (ab Punkt B) hätte.
Das Modell beruht auf folgenden Prämissen:
1 With
a capital “D” and “E”!
15
ˆ Die Produktionsfaktoren sind substituierbar
ˆ Die Produktionsfaktoren sind in beliebig kleinen Mengen einsetzbar (stetige Teilbarkeit der Inputfaktoren)
ˆ Ein qualitativ gleichbleibendes einziges Produkt wird erzeugt
ˆ Der Gesamtbetrieb wird betrachtet
ˆ Produktionstechnik ist konstant
ˆ Statische Betrachtungsweise
ˆ Es besteht eine direkte Beziehung zwischen Input und Output
Es ergeben sich zwei Betrachtungsweisen:
1. x = x(r1 , c): Es wird nur ein Faktor variiert, alle anderen bleiben konstant
(ceteris paribus–Annahme)
2. x = x(r1 , r2 , c): Zwei Faktoren werden variiert (Partielle Faktorvariation2 )
Totale Faktorvariation
Damit wir die Produktionsfunktionen auch mathematisch handhaben können,
müssen noch einige Begriffe geklärt werden, die aber alle aus der totalen Faktorvariation heraus entstanden sind:
n
dx =
X ∂x
∂x
∂x
· dr1 + · · · +
· drn =
· ri
∂r1
∂rn
∂ri
i=1
Grenzertrag
Der Grenzertrag eines Produktionsfaktors i ist folgendermaßen definiert:
GE =
∂x
∂ri
und gibt die Änderung des Ertrags für eine marginale Änderung des Inputfaktors i an.
Durchschnittsertrag
Und auch noch der Durchschnittsertrag, der folgendermaßen definiert ist:
DE = ei =
x
ri
Der Durchschnittswert ergibt sich aus der Division des Ordinatenwerts in
einem bestimmten Punkt der Gesamtertragsfunktion durch den dazugehörigen
Abszissenwert. Es ergibt sich die Steigung eines Fahrstrahls aus dem Ursprung
(tan α).
2 Die partielle Faktorvariation ist die totale Faktorvariation bei Veränderung nur eines
Inputfaktors
16
Es gilt: im Maximum der Durchschnittsertragskurve ist der Durchschnittsertrag gleich dem Grenzertrag. Dieses läßt sich mehr oder weniger trivial mathematisch zeigen:
ei
=
dei
dri
=
x(ri , c)
ri
∂x
∂ri ri − x
ri2
!
=0
Die Ableitung wurde mit der Quotientenregel vollführt. Einfaches umformen
liefert uns nun:
ri
∂x
=x
∂ri
Multiplizieren mit (1/ri ) liefert uns die gewünschte Größe:
∂x
x
=
∂ri
ri
was unserem Durchschnittsertrag ei entspricht.
Dieses läßt sich auch intuitiv begründen. Solange der Grenzertrag über dem
Durchschnittsertrag liegt, erhöht jede weitere Einheit des Outputs den Durchschnittsertrag. Liegt der Grenzertrag jedoch unter dem Durchschnittsertrag,
sinkt dieser bei jeder weiteren Einheit, da die weitere Einheit weniger Ertrag
liefert als der Durchschnitt aller anderen bis jetzt.
Produktionselastizität
Die Produktionselastizität (εx,ri ) gibt die prozentuale Veränderung des Outputs
bei 1% er Veränderung des Inputfaktors ri an. Sie ist definiert als dem Verhältnis
von Grenzertrag und Durchschnittsertrag.
εx,ri =
∂x ri
∂x/∂ri
Grenzertrag
·
=
=
∂ri x
x/ri
Durchschnittsertrag
Die Produktionsfunktion vom Typ A ist keine Iso–Elastische Funktion,
da sich εx,ri entlang der Produktionsfunktionskurve ändert.
Grenzrate der Substitution
Die Grenzrate der Substitution (GRS) wird aus dem totalen Grenzprodukt für
den 2–Faktoren Fall gewonnen.
dx =
∂x
∂x
· dr1 +
· dr2
∂r1
∂r2
Für dx = 0 folgt:
dr2
∂x/∂r1
=−
dr1
∂x/∂r2
17
Die GRS ist somit gleich dem negativen, umgekehrten Verhältnis der Grenzproduktivitäten. Sie sagt aus, um wie viele Einheiten Faktor 2 verändert werden
muß, um bei gleichem Output die Menge des Faktors 1 um eine Einheit verringern zu können.
Das Vierphasenshema des Ertragsgesetzes
Da jetzt alle Grundbegriffe erklärt sind, können wir die Abb (C–6) in der Foliensammlung untersuchen. Das Ertragsgesetz läßt sich in vier Phasen aufspalten:
1. Phase: erstreckt sich bis zum Maximum der Grenzertragsfunktion
ˆ Gesamtertrag: positiv und steigend
ˆ Grenzertrag: positiv und steigend
ˆ Durchschnittsertrag: positiv und steigend
ˆ Produktionselastizität: positiv und fallend
2. Phase: endet beim Maximum des Durchschnittsertrags
ˆ Gesamt- und Druchschnittsertrag: positiv und steigend
ˆ Grenzertrag und εx,ri : positiv und fallend
3. Phase: bis zum Maximum der Gesamtertragsfunktion
ˆ Gesamtertrag: positiv und steigend
ˆ Grenz- und Durchschnittsertrag, εx,ri : positiv und fallend
4. Phase: beginnt am Maximum der Gesamtertragsfunktion
ˆ Gesamt- und Durchschnittsertrag: positiv und fallend
ˆ Grenzertrag und εx,ri : negativ und fallend
3.3.2
Die Cobb–Douglas Produktionsfunktion
Untersuchungen haben ergeben, daß die französische Gasindustrie Anfang der
50er Jahre des 20. Jahrhunderts Produktionsfunktionen hatten, die den Anforderungen einer Cobb–Douglas zumindest annähernd entsprachen. Da diese
Produktionsfunktion auch in allen anderen wirtschaftwissenschaftlichen Veranstaltungen gerne benutzt wird, sollte man sich also davor hüten, sie als nicht
realitätsnah zu verschimpfen!
ˆ Substitutionalität der Inputfaktoren
ˆ stetige Teilbarkeit aller Produktionsfaktoren.
ˆ von Anfang an positive aber fallende Grenzproduktivitäten
Für den zwei Inputfaktoren Fall sieht die CD Produktionsfunktion z.B. folgendermaßen aus:
(α) (1−α)
x = c · r1 r 2
mit
0≥α≥1
und c > 0
als ein Beispiel einer linear–homogenen Produktionsfunktion
18
Homogenität
Allgemein gilt: eine Funktion ist homogen vom Grad n falls gilt:
f (kr1 , . . . , krn ) = k n · x
ˆ Für n = 1 gilt der Spezialfall einer linear–homogenen Funktion. Bei einer
Produktionsfunktion spricht man von konstanten Skalenerträgen.
ˆ Für n > 1 erhält man eine überproportionale Steigerung des Outputs x
bei Erhöhung von ri
ˆ Für n < 1 erhält man eine unterproportionale Variation von x
3.3.3
Leontieff Produktionsfunktionen
Die Leontieff Produktionsfunktion ist ein Beispiel für eine linear–limitationale
Produktionsfunktion. Die Produktionsfaktoren sind nicht beliebig substituierbar, nur in einem bestimmten konstanten Mengenverhähltnis wirkungsvoll einsetzbar.
Im 2 Faktorenfall wird
r1 = a1 · x und r2 = a2 · x
eingesetzt. Hieraus folgt sofort:
r1 =
a1
r2
a2
Aus r2 = fix müssen a1 /a2 Einheiten r1 eingesetzt werden für ein ökonomisch sinnvolles Ergebnis. Ein Mehreinsatz von r1 führt nicht zu einer Outputerhöhung.
3.3.4
Produktionsfunktion vom Typ B
An diese Produktionsfunktion (auch Gutenberg Produktionsfunktion genannt) werden folgen Anforderungen gestellt:
1. Keine unmittelbare Beziehung zwischen Einsatzfaktoren und Ertrag
2. Mittelbarer Zusammenhang: technische Stellgrößen schieben sich zwischen
Input und Output
3. Variierbarkeit der Einsatzfaktoren ist nicht unbegrenzt gegeben
Allgemeine Beschreibung des Produktionsprozeßes
ˆ Kombination von Produktionsfaktoren
ˆ Potentialfaktoren: Nutzungsdauer ist abhängig von deren intensitäts- und
zeitmäßigen Beanspruchung
ˆ Repetierfaktoren: Nutzung abhängig von der intensitäts- und zeitmäßigen
Beanspruchung der Potentialfaktoren
19
Ausgehend von diesen Beobachtungen und Prämissen hat Gutenberg seine“
”
Produktionsfunktion als ein System von Mengenverbrauchsfunktionen gesehen: wieviel der Repetierfaktoren eingesetzt werden müssen in Abhängigkeit
von der zeitlichen und intensitätsmäßigen Inanspruchnahme der Potentialfaktoren.
Das Kostenminimum erhält man durch eine Fallunterscheidung.
1. Fall: variiere die Intensität bei gegebener Einsatzzeit
Beliebige Teilfaktoren j haben jeweils gewisse technische Eigenschaften die uns
zur z–Situation führen: zj1 , zj2 , . . . , zjv . Gesucht ist die Einsatzmenge der Repetierfaktoren bei gegebenem Output und Zeit, bei gegebener technischer Z–
Situation und variierbarer Intensität dj , definiert als Output von j pro Zeiteinheit.
Dazu bedienen wir uns der Mengenverbrauchsfunktionen.
1. Variation der Intensität dj :
rij = fij (zj1 , . . . , zjv ; dj ) ∀ i, j
|
{z
}
konstant
2. Da wir die z–Situationen außer Acht lassen, schreiben wir:
rij = fij (dj ) ∀ i, j
3. Die Intensität dj ist abhängig von der Outputmenge x:
dj = aj (x)
4. Es folgt der mittelbare Zusammenhang:
rij = fij (aj (x))
∀ i, j
5. Woraus sich für den Gesamtbetrieb ergibt:
ri =
m
X
j=1
rij =
m
X
fij (aj (x))
∀i
j=1
Es ergibt sich also die Gesamteinsatzmenge des Repetierfaktors i, bei jeweils vorgegebener Outputmenge x und Zeit (Produktionszeit).
2. Fall: variiere die Einsatzzeit bei gegebener Intensität
6. Die Produktionszeit des Aggregats j ist gegeben als tj .
rij = gij (tj ) ∀ i, j
7. Die zeitliche Benutzung des Aggregats ist abhängig von der Outputmenge:
tj = bj (x) ∀ j
20
8. Es folgt der mittelbare Zusammenhang:
rij = gij (bj (x))
∀ i, j
9. Woraus sich für den Gesamtbetrieb ergiebt:
ri =
m
X
rij =
j=1
m
X
gij (bj (x))
∀i
j=1
3. Fall: Verbrauchsminimale Kombination von Intensität und Zeit
Wie gezeigt, ist rij determiniert durch die Intensität dj und die Produktionszeit
tj . Für ein einziges Aggregat ist die Produktionsfunktion demnach x = dj · tj .
Interessanter ist da schon der fall für m Aggregate:
x=
m
X
d j · tj
j=1
Gesucht werden jetzt noch die kostenoptimalen Intensitäten und Produktionszeiten. Da die Produktionstheorie jedoch nur Mengengerüste behandelt,
bringt uns diese Fragestellung direkt zur Kostentheorie, die Wertgerüste behandelt.
3.4
Grundlagen der Kostentheorie
Kosten ist ein bewerteter, leistungsbedingter Güterverzehr materieler und immaterieller Güter. Ein mengenmäßiger Güterverbrauch liegt vor, der zu bewerten ist. Dagegen wird sachzielbezogen bewertet: nur der Güterverbrauch, der
für die betriebliche Leistungserstellung notwendig war wird bewertet.
Aufgaben der Kostentheorie
ˆ Erkennen und systematisieren von Kosteneinflußgrößen
ˆ Aufzeigen von deren Wirkung auf die Kostenhöhe
ˆ Formulierung von Kostenfunktionen
ˆ Festlegung der beeinflußbaren Kosten
Kosteneinflußgrößen
ˆ Faktorpreise
ˆ Faktorqualität
ˆ Fertigungsprogramm
ˆ Beschäftigungsgrad
ˆ Betriebsgröße
21
3.4.1
Kostenfunktionen
Eine Kostenfunktion K = K(x) gibt den funktionalen Zusammenhang der Kosten und der Outputmenge an.
Auf der Basis der Produktionsfunktion vom Typ A definieren wir i als Index
der Produktionsfaktoren, qi als Kosten des Produktionsfaktors pro Einheit und
ri wie üblich als der Einsatzmenge des Produktionsfaktors i. Daraus ergibt sich:
qi · ri = Kosten des Produktionsfaktors i
und die Produktionsfunktions von Typ A kann wie folgt umgeschrieben werden:
x = x(r1 , . . . , rn )
mit der zugehörigen monetären Produktionsfunktion:
x = x(r1 q̄1 , . . . , rn q̄n )
|
{z
}
ges. var. Kosten
Womit wir x = x(Kg −KF ) = x(Kv ) in Abhängigkeit der gesamten Variablen
Kosten (Gesamtkosten minus Fixkosten) hätten.
Aus der Umkehrfunktion zur monetären Produktionsfunktion erhalten wir
die Variable Kosten–Funktion:
x = x(Kv )
Kv = Kv (x)
Unter zusätzlichen Berücksichtigung der Fixkosten KF erhalten wir die Gesamtkostenfunktion Kg = Kv + KF als Spiegelung der monetären Produktionsfunktion bei partieller Faktorvariation. (Sh. auch Folie C–16 der Foliensammlung)
Es gilt: Im Minimum der gesamten Durchschnittskosten3 k = K(x)/x sind
die Durchschnittskosten gleich den Grenzkosten K 0 . Hierfür wenden wir wieder
Mathematik der Schulzeit an.
Als notwendige Bedingung für ein Minimum muß die erste Ableitung von
k = K(x)/x gleich Null sein:
x·
∂k
=
∂x
dK
dx
− K(x) !
=0
x2
Multiplizieren mit x2 und die daraus folgende Geleichung umformend erhalten wir:
K(x)
dK
=
= K0
x
dx
und somit den Beweis für die notwendige Bedingung.
k=
Es gilt außerdem: Im Minimum der variablen Durchschnittskosten kv =
Kv (x)/x die variablen Stückkosten gleich den Grenzkosten K 0 .
Analog zum vorherigen Beweis“ untersuchen wir die notwendige Bedingung
”
für ein Minimum:
3 Stückgrößen
haben kleine Buchstaben, Gesamtgrößen große!
22
dKv (x)
· x − Kv (x) !
dkv
= dx
=0
dx
x2
Umformen bringt uns zur Gleichung
x·
dKv (x)
= Kv (x)
dx
oder aber
dKv (x)
Kv (x)
=
= kv
dx
x
Womit wir uns beruhigt zurücklehnen und uns auf die Schulter klopfen
können ob unseren herausragenden mathematischen Fähigkeiten.
Betriebsminimum und –optimum
Mit diesen Vorüberlegungen können wir uns jetzt Gedanken zum Betriebsminimum machen. Als kurzfristige Preisuntergrenze gilt das Minimum der variablen Stückkosten. Wenn ein Unternehmen nicht mindestens seine laufenden
Kosten mit dem Erlös decken kann, wird es den Betrieb einstellen. Jede weitere
verkaufte Einheit des Gutes bringt nur mehr Verluste.
Für das Betriebsoptimum dagegen ist die langfristige Preisuntergrenze
beim Minimum der gesamten Stückkosten (incl. der Stückkosten) gegeben. Wenn
das Unternehmen nicht mindestens seine Gesamtkosten decken kann, wird es auf
lange Sicht den Betrieb einstellen.
3.4.2
Minimalkostenkombination
Die Minimalkostenkombination (MKK) gibt jene Kombination von Faktoreinsatzmengen an, für die die Gesamtkosten der zur Produktion einer bestimmten
(vorgegebenen) Ausbringungsmenge x benötigten Produktionsfaktoren minimal
sind. Es muß folglich eine Substitution der Inputfaktoren möglich sein.
Ausgangspunkt:
ˆ spezielle Ertragsisoquante mit x = x1
ˆ wenn r22 auf r21 sinkt, so muß r11 auf r12 steigen, damit weiterhin der
Output x1 produziert wird.
ˆ Substitutionsverhältnis der Produktionsfaktoren 1 und 2:
∆r2
r22 − r21
=
∆r1
r11 − r12
ˆ für infinitesimal kleine Änderungen erhalten wir die Grenzrate der Substitution (GRS):
∆r2
dr2
lim
=
= GRS
∆r1 →0 ∆r1
dr1
23
Es gilt: Die Grenzrate der Substitution entspricht dem reziproken Verhältnis
der Grenzproduktivitäten beider Faktoren mit negativen Vorzeichen.
Beweis: aus dem totalem Grenzprodukt für zwei Faktoren folgt:
dx =
∂x
∂x
!
· dr1 +
· dr2 = 0
∂r1
∂r2
Was wir auch schreiben können als:
∂x
· dr1
∂r1
= −
∂x
· dr2
∂r2
dr2
dr1
= −
∂x/∂r1
∂x/∂; r2
⇒
Herleitung der MKK
Im 2 Faktorenfall sind die Preise pro Mengeneinheit der Produktinsfaktoren als
q1 , q2 bezeichnet. Die Kostenfunktion unter der Annahme von KF = 0 läßt sich
somit schreiben als
K = q 1 · r1 + q 2 · r2
oder durch Auflösen nach r2 als
r2 =
K
q1
−
· r1
q2
q2
Ist ein K fest vorgegeben, so resultiert eine Kostenisoquante als einfacher
linearer Zusammenhang.
Gesucht ist die kostenminimale Kombination der Faktoren für einen bestimmten, vorgegebenen Output x. Die vorhandene Ertragsisoquante für x̄ liefert uns das Ergebnis als Tangentialpunkt. Vergleiche dazu auch Folie C–18 der
Foiliensammlung.
Als Ergebnis erhalten wir, daß die Steigung der Ertragsisoquante
dr2
∂x/∂r1
=−
dr1
∂x/∂r2
gleich der Steigung der Kostenisoquante
dr2
q1
=−
dr1
q2
sein muß. Damit wissen wir, daß für eine kostenminimale Kombination das
Verhältnis der Grenzproduktivitäten gleich dem Verhältnis der Preise ihrer Produktionsfaktoren sein muß:
∂x/∂r1
q1
=
∂x/∂r2
q2
Für den allgemeinen Fall von n Produktionsfaktoren muß gelten:
∂x
∂x
∂x
÷
÷ ··· ÷
= q1 ÷ q2 ÷ · · · ÷ qn
∂r1
∂r2
∂rn
24
Alternative Herleitung der MKK (nach Lagrange)
Eine alternative Möglichkeit die optimalen Einsatzmengen r1 und r2 zu ermitteln ist der Lagrange–Ansatz. Gegeben sind: x, q1 , q2 und gesucht sind r1 , r2 .
Dazu stellen wir uns eine Larange Funktion L auf:
L = q1 r1 + q2 r2 − λ [x(r1 , r2 ) − x̄]
Aus den ersten beiden Ableitungen
∂L
∂x !
= q1 − λ ·
= 0 und
∂r1
∂r1
∂L
∂x !
= q2 − λ ·
=0
∂r2
∂r2
erhalten wir nach Auflösen nach λ und gleichsetzen:
∂x/∂r1
q1
=
∂x/∂r2
q2
unsere schon bekannte Bedingung für eine Minimalkostenkombination für
den 2 Faktoren Fall.
3.4.3
Kostenfunktion für den Typ B
Es besteht ein mittelbarer Zusammenhang von Inputfaktoren und Outputmenge. Es sind folgende Anpassungen an Beschäftigungsschwankungen möglich:
ˆ kurzfristig gelten keine unmittelbaren Beziehungen zwischen Input und
Output:
– intensitätsmäßig (Variation der Intensität)
– zeitlich (Variation der Produktionszeit)
ˆ langfristig bestehen unmittelbare Beziehungen:
– quantitativ i. e. S. (Stilllegung und Aufnahme von Anlagen → alle
Anlagen sind langfr. kosten- und funktionsgleich)
– selektiv (unwirtschaftliche Anlagen werden stillgelegt → qualitative
Unterschiede in den Anlagen liegen vor)
Kostenfunktion bei intensitätsmäßiger Anpassung
Als Ausgangspunkt nehmen wir die Mengenverbrauchsfunktion
rij = fij (aj (x))
∀ i, j
woraus wir unter Hilfenahme des Faktorpreises qi eine Kostenleistungsfunktion erstellen können:
Kij = rij qi = fij (aj (x)) · qi
∀ i, j
Die Kostenleistungsfunktion entspricht den Kosten für einen Faktor i an
einem Aggregat j für unterschiedliche Outputmengen x. Hieraus müssen wir
eine Gesamtkostenfunktion für alle Aggregate j erstellen:
25
Kj =
X
rij qi
=
j
X
fij (aj (x)) · qi
X
fij (dj ) · qi
i
=
∀j
i
Womit wir eine unmittelbare Abhängigkeit fij (dj ) geschaffen hätten. Die
Gesamtkostenfunktion für den Betrieb zu erstellen ist nun ein leichtes:
∗
K=
X
j
Kj =
XX
j
fij (aj (x)) · qi + ggfs.
r
X
sr (x) · qr
r
i
Pr∗
Der Additive Anhang“ r sr (x)qr wird benötigt, um gegebenenfalls auf”
tauchende intensitätsmäßig unabhängige Faktoreinsatzmengen zu berücksichtigen.
Kostenfunktion bei zeitlicher Anpassung
Jetzt wird nur die Produktionszeit variiert, die Intensität dagegen exogen gegeben.
Kj =
X
rij qi
=
j
X
gij (bj (x)) · qi
X
gij (bj (x))
j
=
∀i
j
wegen rij = gij (tj ) = gij (bj (x))
∀j
Für den Gesamtbetrieb ergiebt sich:
XX
K=
rij · qi
j
i
Annahme: bei gegebener Intensität sind die variablen Kosten pro Zeiteinheit
konstant (→ lj )
Lj = lj tj = lj tj (x) ∀ j
Kombinierte zeitliche und intensitätsmäßige Anpassung
Ausgangspunkt:
ˆ verschiedene (hier: zwei) funktionsgleiche, aber kostenverschiedene Aggregate A und B
ˆ Intensität und Einsatzzeit ist innerhalb vorgegebener Grenzen variabel
Bekannt ist die Ausbringungsmenge x = x̄, es ergibt sich also wieder einmal die Frage nach der kostenminimalen zeitlichen und intensitätsmäßigen Ausnutzung der beiden Aggregate um die vorgegebene Menge x̄ herzustellen. Die
Entscheidungsparameter sind also das Leistungsniveau und die Zeit.
Dazu geht man in folgender Reihenfolge vor:
26
opt
1. Man suche die optimalen Intensitäten der beiden Aggregate: dopt
A und dB
opt
2. Man bestimme die dazu gehörenden Stückkosten kv (dopt
A ) und kv (dB )
3. Entscheidung: Auswahl des stückkostenminimalen Aggregats und zeitlicher Anpassung desselben bis die maximale Produktionszeit erreicht ist.
Frage: ist die vorgegebene Ausbringungsmenge x̄ erreicht?
4. Falls nicht, dann bei gegebener maximaler Produktionszeit so lange eine
intensitätsmäßige Anpassung durchführen, bis die Grenzkosten des eingesetzten Aggregats dem Minimum der Stückkosten des nicht eingesetzten
Aggregats gleichen oder die maximale Intensität erreicht ist.
5. Ist x̄ immer noch nicht erreicht, dann so lange bei optimaler Intensität eine
zeitliche Anpassung des zweiten Aggregats vollführen, bis die maximale
Produktionszeit erreicht ist.
6. Ist die maximale Einsatzzeit erreicht, dann eine intensitätsmäßige Anpassung beider Anlagen bis das jeweilige Maximum oder der vorgegebene
Output erreicht ist.
Prinzip: Die jeweils zusätzliche Produktion soll mit den geringsten Grenzkosten geschehen.
27
Kapitel 4
Absatz
4.1
Einführung
Marketing:
4.1.1
Planung, Realisierung und Kontrolle von Programmen,
mit deren Hilfe gewünschte Austauschprozesse mit ausgewählten Märkten geschaffen, aufgebaut und aufrechterhalten werden sollen, um betriebliche Ziele zu verwirklichen.
Marketingziele
Marketingziele können zweierlei Art sein: ökonomische Ziele wie z.B.
ˆ Gewinnziele
ˆ Umsatzziele
ˆ Marktanteilsziele
oder können auch nicht–ökonomische Ziele enthalten. Unter diesen kennt
man
ˆ Psychologische Ziele
– Imageziele
– Bekanntheitsgrad
ˆ Streutechnische Ziele
– meist innerhalb der Kommunikationspolitik
4.1.2
Marketinginstrumente
Bei den Marketinginstrumenten sind die vier p’s gut zu merken: Price, Place,
Product und Promotion. Anders, und vor allem länger ausgedrückt erstrecken
sich die Instrumente auf
ˆ Produkt-, Sortiments- und Servicepolitik
28
ˆ Kontrahierungspolitik
ˆ Kommunikationspolitik
ˆ Distributionspolitik
Des weiteren gibt es verschiedenste Faktoren die das Betriebsmarketing beeinflussen können. Dazu zählen rechtliche Vorschriften, (Absatz-) Marktcharakteristika wie Marktgröße oder -volumen, sowie weitere Einflußgrößen wie Selbstbeschränkungen und die eigene Betriebgröße.
4.2
Produkt- und Sortimentspolitik
Produkt:
Menge von Eigenschaften, die kombiniert werden um
ein oder mehrere Bedürfnisse zu befriedigen. Es kann
Gegenstand eines Tausches sein, um Ziele des Anbieters
zu befriedigen.
ˆ Funktionale Produkteingenschaften
–
–
–
–
Qualität
Design
Verpackung
Funktionsfähigkeit
ˆ Immaterielle Produkteigenschaften
–
–
–
–
Marke
Image
Serviceleistungen
Gewährleistungen
Immaterielle Produkteigenschaften gewinnen zunehmend an Bedeutung, da
die Produkte immer austauschbarer werden. Die Funktionalität ist bei den meisten Produkten aus der selben Produktfamilie ähnlich, gleich von welcher Firma
sie hergestellt werden.
Ziele der Produktpolitik
ˆ Gewinnziele
ˆ Umsatzziele
ˆ Marktanteilsziele
ˆ Kostensenkung
ˆ Beschäftigungsglättung
ˆ Risikostreuung
ˆ Qualitätssteigerung
Restriktionen sind vor allem betrieblicher Art. Kapazitive und personelle
Restriktionen sowie fehlendes Know-How sind neben rechtlichen Restriktionen
die größten Hürden der Produktpolitik.
29
Handlungsmöglichkeiten der Produktpolitik
1. Produktinnovation: beinhaltet Suche, Auswahl und Einführung eines
neuen Produkts auf den Markt. Dabei kann es sich um eine
ˆ Marktneuheit handeln. Hierbei handelt es sich um eine echte Neuerung, da auf dem Markt bisher kein vergleichbares Produkt existiert.
Der Hersteller agiert hier als Innovator.
ˆ Betriebsneuheit handeln. In diesem Fall existierte das Produkt bereits auf dem Markt, die Firma stellt das Produkt jedoch zum ersten
Mal her. Der Hersteller agiert hier als Imitator.
2. Produktvariation: an einem bereits existierenden Produkt werden Eigenschaften verändert. Man nennt dieses ein Face Lifting, falls es sich um
ein Automobil handelt, ansonsten einen Relaunch.
3. Produktdifferenzierung: ist eng mit der Produktvariation verbunden.
Es werden jedoch neue Produkte hergestellt (z.B. eine Spar- und eine
Luxusvariante eines Produkts), das Angebot weitet sich aus.
4. Produkteliminierung: ein Produkt wird vom Markt genommen.
Produktlebenszyklus
Die Handlungsmöglichkeiten geben auch den Produktlebenszyklus wider. Jedes
Produkt veraltet irgendwann und muß vom Markt genommen werden. Soll das
Unternehmen dauerhaft am Markt bestehen, muß Produktinnovation betrieben
werden. Eine Produktdifferenzierung und -variation kann die Produkteliminierung um einige Zeit herausschieben.
1. Einführung: hohe Kosten, geringe Absatzmenge
2. Wachstum: Erlöse steigen überproportional
3. Reifephase: Erlöse steigen, Gewinne stagnieren jedoch; hier wird meist
über eine Produktvariation oder -differenzierung nachgedacht
4. Sättigungsphase: Verdrängungswettbewerb, Gewinne sinken
5. Degeneration: Erlöse fallend, Verluste
4.2.1
Produktinnovation
Gründe für neue Produkte können betriebsintern oder auch betriebsextern vorliegen. Betriebsextern sind technischer Fortschritt oder geänderte Verbraucherverhaltensweisen als Beispiel zu nennen. Betriebsintern kann man Existenz- oder
Wachstumssicherung und Risikostreuung als Gründe nennen.
Gewinnung von Produktideen
Zur Gewinnung von neuen Produktideen kann man sich auf intuitiv–kreative
Möglichkeiten wie Synektik“ oder das Brainstorming“ verlassen, oder auf
”
”
systematisch–logische Ansätze wie z.B. auf analytisch–kombinative Denkprozesse zurückgreifen.
30
Grobauswahl von Produktideen
Ist man durch die verschiedenen Verfahren zu vielen Produktideen gekommen,
so muß man im zweiten Schritt sich für eine, oder auch mehrere entscheiden.
Dazu kann man sich wieder des Hilfsmittels eines Scoring Modells bedienen.
1. Auswahl der Beurteilungskriterien
2. Gewichtung der Kriterien
3. Operationalisierung der Kriterien → Skalierung
4. Messung der Erfüllung der Kriterien durch die jeweilige Produktidee
5. Bildung der gewichteten Gesamtpunktzahl GGPZ für alle Produktideen
und Auswahl des Produkts mit höchster GGPZ
GGPZj =
n
X
gi · eij
∀j
i=1
mit eij als dem Erfüllungsgrad der Produktidee j im Hinblick auf das
Kriterium i.
Natürlich ist auch hier Vorsicht geboten, da diese Methode nicht perfekt ist.
ˆ qualitative und quantitative Kriterien können berücksichtigt werden
ˆ Bestimmung des Skalierungsfaktors kann problematisch sein
ˆ Kriterien dürfen sich nicht überschneiden (disjunkte Kriterien)
ˆ schlechte und gute Kriterien gleichen sich aus (hier kann mit einer Mindestpunktzahl in den einzelnen Kriterien Abhilfe geschaffen werden)
ˆ das Ergebnis ist nur eine Auswahl unter den Wahlmöglichkeiten, es muß
nicht notwendigerweise eine gute oder gar die beste Produktidee sein
Wirtschaftlichkeitsanalyse, Feinauswahl
Bei der Wirtschaftlichkeitsanalyse werden nach einer bereits vorgenommenen
Grobauswahl die einzelnen Innovationsmöglichkeiten hinsichtlich ihrer Rentabilität geprüft. Der prognostizierte Ertrag muß größer gleich den prognostizierten
Kosten sein. Dieses kann durch Mittel der Finanzierungsrechnung geprüft werden.
Der Kapitalwert ist ein dynamisches Verfahren. Man nimmt dabei an, daß
sich ein Projekt mit der Rate i verzinst. Ist der Kapitalwert C0 also ≷ 0, so ist die
Verzinsung ≷ i. Ein Kapitalwert von größer Null ist somit für die Durchfürung
entscheidend.
C0 = −K0F+E +
n
X
(pt − kvt ) · xt − KtF · (1 + i)−t
t=1
mit (pt −kvt ) als Stückdeckungsbeitrag und (1+i)−t als Diskontierungsfaktor
mit der Verzinsung i.
31
Die Break–Even–Analyse ist ein statisches Verfahren. Hierbei wird der
Erlös den Kosten gleichgesetzt, die daraus resultierende Ausbringungsmenge
x∗ ist die Ausbringungsmenge, bei der zumindest die Kosten K = Kv + K F
gedeckt sind.
!
E = K
p · x = kv · x + K F
KF
x = x∗ =
(p − kv )
Diese Methode ist vorteilhaft bei kleineren prognostizierten Absatzmengen.
Verschiedene Tests
ˆ Produkttests: Prüfung des neuen Produkts
– Konzeptionstest: vor der eigentlichen Produktentwicklung; Verbesserungen sind noch möglich
– Produkttest i. e. S.: Tests mit Prototypen
– Namestest: nicht das Produkt, nur der Name wird getestet
*
*
*
*
Erinnerungswirkung
Assoziationswirkung
Möglichkeiten des rechtlichen Namesschutzes
internationale Ausprechbarkeit
– Verpackungstest: Test der technischen und kommunikativen Möglichkeiten der Verpackung
* Entsorgungsfunktion
* Rechtliche Gegebenheiten (Mogelpackung)
* Kennzeichnungsrechte und -pflichten
ˆ Markttests: probeweiser, kontrollierter Verkauf unter Marktbedingungen
– Regionaler Markttest: Produkt wird in einem regionalem Teilgebiet
angeboten; Teilgebiet sollte representativ sein
– Storetest: Produkt wird in wenigen Geschäften angeboten
* Real: Produkt wird in der realen Welt in einige Geschäfte gestellt
* Labor: ein künstliches Geschäft wird geschaffen
4.2.2
Produktvariation
Es werden ausgewählte Eigenschaften verändert. Es ergibt sich die Frage nach
der Vorteilhaftigkeit der Variation. Um diese zu beantworten wird folgender
statischer Vergleich herangezogen:
1. Festlegung der zu verändernden Eigenschaften
32
2. Prüfung der Wirtschaftlichkeit der Veränderungen: die zusätzlichen Erlöse
müssen die zusätzlichen Kosten decken.
Galt
Gneu
= (palt − kvalt )xalt − KFalt
F+E
= −Kvar
+ (pneu − kvneu )xneu − KFneu
3. Bei Vorteilhaftigkeit: Festlegung des Variationszeitpunktes
4.2.3
Produktdifferenzierung
Man erreicht eine Ausweitung des Sortiments durch zusätzliches Angebot von
Produktvarianten, wie z.B. eine Luxus- oder eine Sparvariante des Produkts.
Wieder hilft uns ein statischer Vergleich, um die Vorteilhaftigkeit der Differenzierung erkennen zu können.
Gohne
=
(p − kv )x − KF − K MA
Gmit
=
J
X
j=1
KjF+E +
J
X
(pj − kvj )xj − KFj − KjMA
j=1
Mit j = 1, . . . , J als Anzahl der Produktinnovationen. Ein sukzessiver Aufbau über alle J ist nötig, da jede Variante so einzelnd betrachtet wird. Vorsicht
ist dennnoch geboten, da die Varianten meist substitutiv zueinander sind.
4.2.4
Produkteliminierung
Es geht hierbei um die Entscheidung über die endgültige Herausnahme eines
Produkts vom Markt. Umsatzschwache Produkte binden viele Managementkapazitäten und können einen negativen Einfluß auf das Unternehmensimage
haben. Vorsicht bei Eliminierung von komplementären Gütern ist geboten, da
hier Acht auf die Absatzverbundwirkungen gehalten werden muß.
Eine Umsatzanalye per Lorenzkurve zeigt die Umsatzverteilung aller Produkte im Unternehmen an. Das Ziel sollte eine möglichst ausgeglichene Umsatzverteilung sein.
Die Entscheidung über eine Eliminierung kann über den Deckungsbeitrag
DBiabs getroffen werden. Der Deckungsbeitrag gibt Auskunft über die Höhe des
Geldes, das zur Deckung der Fixkosten nach Abzug der variablen Kosten des
Produkts noch übrig ist.
Gesamtdeckungsbeitrag
Stückdeckungsbeitrag
DBiabs ∀ i
DB/x = dbabs
∀i
i
Ein negativer (absoluter) Deckungsbeitrag zeigt an, daß durch die Produktion noch weitere Verluste entstehen, und kein Geld zur Tilgung der Fixkosten
erwirtschaftet wird. Das Produkt sollte wohl lieber vom Markt genommen werden.
33
4.2.5
Sortimentsplanung
Bei der Sortimentsplanung geht es um das Problem, welche Produkte in welchen
Mengen angeboten werden sollen. Die Sortimentsbreite gibt die Anzahl der
verschiedenen Produktlinien an. Die Sortimentstiefe dagegen die Anzahl der
Artikel pro Produktlinie.
Man unterscheidet zwischen zwei Situationen bei der Sortimentsplanung:
Kein Produktionsengpaß: die Entscheidung über die Produktion wird anhand der Deckungsbeiträge getroffen. Alle Produkte, die positive Deckungsbeiträge besitzen, werden produziert.
!
dbabs
= pi − kvi > 0
i
Vorhandener Produktionsengpaß: die Entscheidung wird anhand der relativen Deckungsbeiträge getroffen.
dbrel
i =
!
dbabs
i
>0
cij
mit cij als Produktionskoeffizienten, der aussagt, wieviel Deckungsbeitrag
das Produkt i in Bezug auf ein knappes Produkt j erwirtschaftet.
Es wird eine Rangordnung nach den relativen Deckungsbeiträgen aufgestellt,
nach dessen die Produkte hergestellt werden, bis die maximale Produktionskapazität erreicht ist.
4.3
Kontrahierungspolitik
Die Kontrahierungspolitik umfaßt die Preis- und die Konditionenpolitik. Grundlage dieser Politiken ist die Gewinnfunktion G(p):
G = p · x(p) − K(x(p))
Der Gewinn entspricht dem Umsatz minus den Kosten.
4.3.1
Grundlagen der Preispolitik
Eigenschaften des Preises
1. Preis hat unmittelbaren Einfluß auf den Gewinn
2. Preis dient als Qualitätsindikator
3. Absatz hängt vom Preis ab
4. Preisänderungen sind schnell und unkompliziert durchführbar
5. Preissenkungen sind schwer rückgängig zu machen
34
Handlungsmöglichkeiten der Preispolitik
ˆ Alternative Preishöhen
– Erstmalige Festlegung bei Produktinnovation und Markteintritt
– Produktlinienpreisbildung (verschiedene Modelle haben unterschiedliche Preisdifferenzen)
– Preisänderungen wegen Nachfrage- oder Kostenänderungen
– Preisänderungen wegen geändertem Konkurrenzverhalten
ˆ Alternative Preisdifferenzierungen (für ein Produkt werden unterschiedliche Preise verlangt)
– Personengruppen (Studentenpreise)
– Einkaufsmenge (Mengenrabatt)
– Verwendungszweck (Heizöl vs. Diesel)
– Zeit (Telefongespräche)
– Raum (Europa Re–Importe bei Autos)
Ziele der Preispolitik
ˆ Sicherung des finanziellen Rückflußes
ˆ Absatzerhöhung
ˆ Gewinnung/Erhaltung von Kunden
ˆ Marktanteilsziele
ˆ Ausschalten der Konkurrenz
ˆ Umsatzziele, Gewinnziele
ˆ [ ... ]
Restriktionen der Preispolitik
ˆ Unternehmensinterne Daten
– Standort
– Betriebsgröße, Branche
– Finanzlage
– Kostensituation
ˆ Unternehmensexterne Daten
– Marktstruktur
– Marktgröße
– Marktform
– Marktbegrenzung
35
ˆ Rechtliche Daten
–
–
–
–
4.3.2
Preisbindung
Preiskartelle
Dumping
Lockvogelpreise
Ansätze der Preistheorie
Preisfindung im Monopol
Das Monopol ist gekennzeichnet durch einen einzigen Anbieter für ein Produkt
und mehrere Nachfrager. Die Preisfindung in diesem Fall ist analytisch einfach.
Prämissen
ˆ keine Konkurrenz (Monopolfall)
ˆ unter Sicherheit bekannte lineare Preisabsatzfunktion
x = a/b − 1/b · p
p = a−b·x
bzw.
ˆ Ziel: Gewinnmaximierung
ˆ Planungshorizont einen Periode
ˆ unter Sicherheit bekannte Kostenfunktion
K = KF + kv · x
Für das Ziel der Gewinnmaximierung müssen wir nur noch die Gewinnfunktion ableiten um dessen Maximum zu erhalten:
G=U −K
= p · x(p) − K(x(p))
= p · x(p) − kv · x(p) − KF
a
1 2
a 1
=
· p − · p − kv
− · p − KF
b
b
b
b
ableiten liefert uns sofort:
dG !
1
= 0 ⇒ p∗ = (a + kv )
dp
2
Der Optimalpreis ergibt sich hier aus dem arithmetrischen Mittel aus Höchstpreis und den variablen Stückkosten.
Alternativ:
G
= p(x) · x − K(x)
= (a − bx)x − kv x − KF
Nach der Ableitung erhalten wir:
dG !
1
= 0 ⇒ x∗ = (a − kv )
dx
2b
36
Preisfindung im Monopol (allgemeiner Fall)
max G = p · x(p) − K(x(p))
Analog zum konkreten Fall wird die erste Ableitung gleich Null gesetzt für
die notwendige Bedingung eines Maximas
dG
dp
dx dK dx !
−
·
=0
dp
dx dp
dK dx
dx
= x+p
=
dp
dx dp
dx p
dK dx p
·
= p+p·
=
dp x
dx dp x
| {z }
| {z }
= x+p
εp
p
·
x
εp
Es folgt sofort:
p + p · εp = K 0 · ε p
p(1 + εp ) = K 0 · εp
εp
p =
· K0
1 + εp
Mit εp als der Preiselastizität der Nachfrage: gibt an, um wieviel prozent
sich die nachgefragte Menge ändert, bei einprozentiger Änderung des Preises.
Der Optimalpreis im Monopol ergibt sich also aus einem elastizitätsabhängiεp
gen Aufschlag auf die Grenzkosten von 1+ε
.
p
Preisfindung im Polypol
Vollk. Polypol:
Viele Käufer und viele Verkäufer stehen sich mit
jeweils sehr geringen Marktanteilen gegenüber, so
daß der einzelne vernachlässigbar ist.
Hinsichtlich der Güter gibt es keine zeitlichen, räumlichen oder persönlichen
Präferenzen (homogener Markt). Es herrscht vollkommene Markttransparenz.
Folge: es bildet sich ein Preis.
Unvollk. Polypol:
Es besteht bezüglich der Anbieter bzw. deren
Produkte Präferenzen seitens der Konsumenten.
In einem unvollkommenen Polypol erhält jeder Polypolist einen Monopoli”
stischen Spielraum“, innerhalb dessen er eine aktive Preispolitik betreiben kann,
ohne daß es zu extremen Mengenwirkungen kommt. Dieser Spielraum ist bedingt durch die Präferenzen der Konsumenten für die Produkte der einzelnen
Anbieter.
37
4.3.3
Praxisorientierte Ansätze der Preisfindung
Kostenorientierte Preissetzung
Diese Methode findet man häufig bei kleineren Unternehmen. Das Ziel ist die
Kostendeckung. Der Preis findet sich also durch einen Gewinnaufschlag g in
Prozent auf die Stückkosten.
p = ks (1 + g/100)
ks bezeichnet die Selbstkosten, die sich aus der Vollkostenrechnung berechnen lassen. Diese enthalten jedoch auch die Gemeinkosten der Fertigung, so daß
es zu einem Problem der Verteilung kommt.
Umgangen werden kann dies, durch die Methode der Einzelkostenbewertung.
Der Preis bestimmt sich so als
p = ke (1 + g ∗ /100)
mit ke als den Einzelkosten der Fertigung. g ∗ > g, da bei der Selbstkostenbestimmung des Preises die Gemeinkosten bereits enthalten sind. Bei der
Einzelkostenbestimmung muß man diese noch abdecken.
Die Probleme sind vor allem, daß die Marktsituationen so nicht berücksichtigt werden, und daß diese Methode einen gefährlichen Zirkelschluß“ darstellt:
”
die Kosten bestimmen den Preis, und dieser wiederum bestimmt die Kosten
über den Fixkostenanteil pro Stück.
Nachfrageorientierte Preisbestimmung
Die Preisabsatzfunktion p = p(x) muß bekannt sein! Diese wird dann in die Gewinnfunktion eingesetzt. Der große Vorteil ist natürlich, daß die Preissetzung
nicht am Markt vorbei verläuft. Es ist aber auch recht aufwendig eine Preisabsatzfunktion zu bestimmen.
Konkurrenzorientierte Preissetzung
ˆ Orientierung am Preisführer
– dominierende Preisführerschaft: Markt ist ungleich verteilt; das Unternehmen mit dem größten Marktanteil wird sich unterordnen, da
ansonsten Sanktionen zu erwarten sind.
– barometrische Preisführerschaft: der Preisführer kann wechseln; Unterordnung an das Unternehmen mit der besten Marktübersicht
ˆ Orientierung am durchschnittlichen Konkurrenzpreis: Preise weichen nicht
wesendlich von den Konkurrenten ab; Mengenbewegungen sind kaum zu
erwarten
38
4.4
Kommunikationspolitik
Definition:
4.4.1
Unter Kommunikationspolitik versteht man die Entscheidungen über die Gestaltung und Übermittlung von
Informationen im Hinblick auf die verfolgten kommunikationspolitischen Ziele, die von seiten der Unternehmen
auf den Absatzmarkt gerichtet sind.
Ziele der Kommunikationspolitik
ˆ Ökonomische Ziele
– Umsatz
– Gewinn
– Marktanteil
ˆ Psychologische Ziele
– Image
– Bekanntheitsgrad
ˆ Streutechnische Ziele
– Kontaktschaffung
4.4.2
Werbung
Werbung ist ein Mittel die Ziele der Kommunikationspolitik zu verwirklichen,
aber bei weitem nicht das einzige.
Werbebudgetierung
Neben den Praktikerverfahren, wie etwa Anteil am Umsatz der Vorperiode, der
Orientierung am Branchendurchschnitt, der Werbebudgetierung als Residualgröße oder der überlegenen Objektive-and-Task“ Methode gibt es noch die
”
theoretischen Optimierungsmodelle, die das Budget nicht willkürlich und prozyklisch aufteilen.
Fall 1: Monoinstrumentales Modell x = x(w) ist bekannt. Hieraus wird
als Ansatz die Gewinnfunktion in Abhängigkeit vom Werbeeinsatz gewählt.
max
G = G(w)
dG
dw
p̄ · x(w) − K(x(w)) − w
dx
dK dx
!
= p̄ ·
−
·
−1=0
dw
dx dw
dx
dK dx
⇒ p̄ ·
=
+1
dw
dx dw
=
Der Grenzerlös entspricht den Grenzkosten plus den Grenzwerbekosten. Der
Absatzfunktion x = x(w) werden im Allgemeinen drei verschiedene Verläufe
unterstellt.
39
1. Lineare Funktion: dies ist zwar einfach zu berechnen, jedoch sehr unrealistisch
2. Degressive Funktion: von Anfang an positive, aber abnehmende Grenzerträge
3. S–förmige Funktion: zuerst überproportionale, dann unterproportionale
Grenzerträge, analog zur Produktionsfunktion Typ A
Fall 2: Polyinstrumentales Modell x = x(p, w) ist bekannt. Dieses wird
wiederum in die Gewinnfunktion eingesetzt.
max
G = G(p, w) = p · x(p, w) − K(x(p, w)) − w
∂G
∂x
dK ∂x
!
= p·
−
−1=0
∂w
∂w
dx ∂w
∂x dK ∂x !
∂G
= x+p·
−
=0
∂p
∂p
dp ∂p
Simultanes Lösen führt zu p∗ und w∗ . Folgende Fehler können an dem Modell
kritisiert werden:
ˆ statisches Modell; die Werbewirkung ist aber dynamisch, da Time–Lag
und Carry–Over Effekte einen wichtigen Teil der Werbewirksamkeiten ausmachen
ˆ Monopolmodell
ˆ Budget gilt als beliebig teilbar
ˆ Jedes w∗ ist realisierbar
ˆ Ausschließlich Gewinnmaximierung als Ziel
ˆ Ermittlung von x = x(w, p) nicht einfach realisierbar
Mediaselection
Bei der Mediaselection (Werbeträgerplanung) spricht man von der Aufteilung
eines gegebenen Werbebudgets auf verschiedene Mediaträger.
Bei der Intermediaselection entscheidet man über die Art des Werbeträgers, so zum Beispiel Radio- oder Fernsehwerbung, oder Werbung im Internet.
Bei der Intramediaselection entscheidet man sich innerhalb eines bereits
ausgewählten Trägers, so zum Beispiel in welcher Zeitschrift man seine Werbung
schalten will.
Tausenderkontaktpreis–Planungsrechnung
Hierbei handelt es sich um den Preis den man bezahlt, um 1000 Personen mit
einer bestimmten Werbung zu erreichen. Hierbei gibt es verschiedene Ansätze,
je nachdem wie viele Informationen man über die Zielgruppe erhalten kann.
40
4.5
4.5.1
TKP1
=
TKP2
=
TKP3
=
Preis pro Anzeige
· 1000
Verkaufte Auflage
Preis pro Anzeige
Leserschaft pro Auflage
Preis pro Anzeige
· 1000
Zielgruppenanteil pro Auflage
· 1000
Distributionspolitik
Grundlagen
Die Distributionspolitik ist unter Marketing gestellt, da bei geringer Lieferzeit
aquisitatorische Potentiale auftreten.
Ziele der Distributionspolitik
ˆ Konfliktvermeidung zwischen Produzent und Handel
ˆ Umsatz, Gewinn, Marktanteil
ˆ Höhe der Distributionskosten
ˆ Steigerung des Distributionsgrads
ˆ Steuerbarkeit des Vertriebsapparats
Restriktionen der Distributionspolitik
ˆ Produkt selbst
ˆ Konsumenten
ˆ Konkurrenz
ˆ Unternehmen selbst
ˆ rechtliche Regelungen
4.5.2
Absatzwegewahl
Hier kann man zwischen direktem Vertrieb und indirektem Vertrieb unterscheiden. Bei ersterem wird das Produkt ohne Einschaltung betriebsfremder
Organe oder Kanäle verkauft, bei letzterem wird der Handel zwischengeschaltet.
Entscheidungskriterien für die Wahl zwischen direktem und indirektem Vertrieb
1. Beeinflußbarkeit der Absatzmenge
2. Kontrollierbarkeit der Absatzmenge
3. Anpassungsmöglichkeiten der Absatzmenge an strukturelle und nachfragemäßige Veränderungen
41
4. Dauerdes Aufbaus eines Vertriebsweges
5. Einfluß auf den Endverbraucherpreis
6. Höhe der Vertriebskosten
7. Erforderlicher Einsatz von Marketinginstrumenten
Der direkte Vertrieb ist in der Regel vorteilhafter bei Gütern mit hoher
Erklärungsbedürftigkeit, bei vergleichsweise wenigen Abnehmern, oder wenn die
Abnehmer regional vergleichsweise stark zentriert ist.
4.5.3
Absatzmittlerwahl
Man kann zwischen einem Handelvertreter HV und einem Reisenden R wählen.
Beide Personen bekommen eine Provision P von ihrem Umsatz, jedoch ist bei
einem Handelvertreter die Provision höher. Unter Umständen bekommen beide
auch noch ein Fixum F , das bei einem Handelvertreter höher ausfällt.
Werden alle diese Daten berücksichtigt, so kann man den kritischen Umsatz
U ∗ bestimmen, ab dem sich der Einsatz eines Handelvertreters gegenüber eines
Reisenden lohnt. Dazu werden die Kostenfunktionen der beiden gleichgesetzt
und nach dem Umsatz aufgelöst.
K HV
KR
= F HV + P HV · U
= FR + PR · U
mit F als dem Fixum und P dem Provisionsanteil vom Umsatz U .
Gleichsetzen und auflösen liefert uns:
F R − F HV
P HV − P R
Kritik ist hier anzubringen, da durch das Gleichsetzen unterstellt wird, beide
Organe erwirtschaften den selben Umsatz. Des weiteren ist es ein statisches
Modell und Reisekosten sind nicht berücksichtigt. Der Handelvertreter trägt
diese meistens selbst. Eine Provisionsstaffelung ist auch nicht in das Modell
eingebaut, die sich aus der Motivationsproblematik ergibt. Daher ist man auf
eine andere Methode gekommen, eine Entscheidung über die Auswahl zwischen
Handelvertreter oder Reisenden zu fällen.
U∗ =
Der Gewinnvergleich
Durch die Gewinnvergleichsrechnung wird die Prämisse für den gleichen Umsatz
durchbrochen. Es wird der Absatzmittler gewählt, der einenen höheren Gewinn
G erwirtschaftet.
GHV
= U HV − K HV
HV
HV
HV
= (p − kv ) · xHV − P
− KF
| {z· x } −F
Provision des HV
GR
= U R − KR
= (p − kv ) · xR −
R
R
P
| {z· x }
Provision des R
42
−F R − KF