Uebungsblatt 6

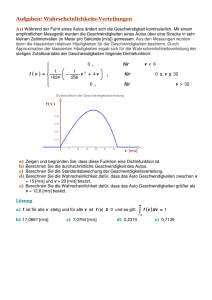
MAT 183: Stochastik für die Naturwissenschaften
FS 2008
Übungsblatt 6
Wahrscheinlichkeitstheorie
Abgabetermin: Mittwoch, 09. April 08, bzw. Freitag, 11. April 08, bei der Semesterassistentin oder beim Semesterassistenten in der jeweiligen Übungsstunde.
Stetige Zufallsgrössen
Aufgabe 62 (2 Punkte):
Die Zufallsvariable U sei auf dem Intervall [5, 10] uniformverteilt. Bestimmen Sie die
Wahrscheinlichkeiten P[8 ≤ U ≤ 8.7] und P[30 ≤ U 2 ≤ 40].
Aufgabe 63 ◦ :
Wir betrachten die Funktion f : R → R, definiert durch


für x < 0 ,

0
f (x) :=
für 0 ≤ x < 1 ,
x


x−3
für x ≥ 1 .
a) Weisen Sie nach, dass f die Dichtefunktion einer stetigen Zufallsgrösse X ist und skizzieren Sie den Graphen von f .
b) Berechnen Sie die Wahrscheinlichkeit P[0.5 ≤ X ≤ 1.5]. Stellen Sie diese Wahrscheinlichkeit im Graphen dar.
c) Wie ist der Median von X zu definieren? Wie gross ist er?
Aufgabe 64 (4 Punkte):
Gegeben ist die Funktion f : R → R,



0
f (x) := 2x − x2


x−4
für x < 0 ,
für 0 ≤ x ≤ 1 ,
für x > 1 .
a) Skizzieren Sie den Graphen von f .
b) Zeigen Sie, dass f die Dichtefunktion einer Zufallsgrösse X ist.
c) Berechnen Sie P[0.75 ≤ X ≤ 2].
d) Wie gross müssen Sie a wählen, so dass P[X ≤ a] = 9/10?
Aufgabe 65 (4 Punkte):
a) Bestimmen Sie die Konstante c so, dass die Funktion f : R → R,
(
c(2x + 1)−2 für x ≥ 0 ,
f (x) :=
0
sonst
1
die Dichtefunktion einer Zufallsgrösse Y ist und zeichnen Sie den Graphen von f .
b) Geben Sie die Verteilungsfunktion von Y an und zeichnen Sie ihren Graphen.
c) Berechnen Sie den Median von Y .
Aufgabe 66 (4 Punkte):
Eine Funktion f mit dem untenstehenden trapezförmigen Graphen soll die Dichtefunktion
einer Zufallsgrösse Z sein.
•
h
...................................
......
...
......
...
......
...
......
...
.
.
......
..
.
......
.
..
......
.
.
......
..
.
......
.
......
...
.
.....
.................
−2 −1
0
1
2
a) Bestimmen Sie die Höhe h.
b) Berechnen Sie P[−1.5 ≤ Z ≤ 1].
Aufgabe 67 (4 Punkte):
a) Bestimmen Sie die Konstante a so, dass die Funktion f : R → R,


für x < 0 ,

0
f (x) :=
4x für 0 ≤ x ≤ a ,


0
für x > a
die Dichtefunktion einer Zufallsgrösse X ist und zeichnen Sie den Graphen von f .
b) Geben Sie die Verteilungsfunktion F von
Graphen an.
√X und ihren
c) Bestimmen sie die Wahrscheinlichkeit P X > 0.5 .
Aufgabe 68 (3 Punkte):
Die Pareto-Verteilung mit den Parametern x0 > 0 und α > 0 ist durch folgende Dichtefunktion f : R → R gegeben:

0
für x < x0 ,
f (x) :=
αxα0 1
für x ≥ x0 .
xα+1
a) Skizzieren Sie den Graphen von f und weisen Sie nach, dass es sich bei f tatsächlich
um eine Dichtefunktion handelt.
b) Sei Y eine Zufallsgrösse mit Dichtefunktion f . Berechnen Sie P[Y > x] und skizzieren
Sie die Verteilungsfunktion von Y .
Anmerkung: Der Name der Verteilung geht auf Vilfredo Pareto (1848-1923) zurück, der
die Verteilung des Volksvermögens in Italien untersuchte. Die Wahrscheinlichkeit P[Y > x]
gibt dabei den Prozentsatz der Bevölkerung mit einem Vermögen von mehr als x an. Der
Paramenter x0 entspricht dabei einem minimalen“ Vermögen, der Parameter α dient zur
”
Skalierung. Pareto fand heraus, dass 80% des Volksvermögens bei nur 20% der Familien
konzentriert war (sog. Pareto-Prinzip oder 80/20-Regel).
Mit der Pareto-Verteilung lassen sich Situationen beschreiben, in denen eine kleine Anzahl
von bewerteten Elementen in einer Menge sehr viel zum Gesamtwert der Menge beiträgt,
2
wohingegen der überwiegende Teil der Elemente nur sehr wenig zum Gesamtwert beiträgt.
Beispiele: Grösse von menschlichen Siedlungen (viele kleine Dörfer mit wenig Einwohnern,
die Masse der Menschen wohnt aber in wenigen grossen Städten), Meteoriteneinschläge auf
dem Mond, Grösse von Dateien die über das Internet ausgetauscht werden, Flächen von
Waldbränden, Anzahl Arten pro Gattung bei Blütenpflanzen (wenige Gattungen bestehen
aus vielen Arten, viele Gattungen aber aus nur wenigen Arten), Wortlängen in längeren
Texten, Grösse von Sandkörnern am Strand u.s.w.
Aufgabe 69 (5 Punkte):
Die Exponentialverteilung mit Rate λ > 0 ist durch die Dichtefunktion f : R → R,
(
0
für t < 0 ,
f (t) :=
λ e−λt für t ≥ 0
gegeben.
a) Skizzieren Sie den Graphen von f und weisen Sie nach, dass es sich bei f tatsächlich
um eine Dichtefunktion handelt.
b) Sei Z eine Zufallsgrösse mit Dichtefunktion f . Berechnen und skizzieren Sie die Verteilungsfunktion von Z.
c) Was ist der Median von Z?
d) Uran U-235 hat eine Halbwertszeit von 7.038 · 108 Jahren. Die (exponentialverteilte)
Zufallsgrösse W misst die Wartezeit eines einzelnen Uran-Atoms bis zu seinem Zerfall.
Wie sieht die Wahrscheinlichkeitsdichte von W aus? (vgl. dazu die Anmerkung)
Anmerkung: Die Exponentialverteilung wird oft verwendet, wenn die Zufallsvariable eine
Wartezeit“ misst, also die Zeit t bis zum Eintreffen eines bestimmten Ereignisses. Das
”
klassische Beispiel dafür ist der Atomzerfall, wo die Dauer bis ein bestimmtes radioaktives
Isotop zerfällt gemessen wird .
In einem radioaktiven Gegenstand gibt es viele aktive Isotope. Der Median den wir in d)
berechnen, entspricht dem Zeitpunkt t̃, wo ein einzelnes dieser Isotope mit Wahrscheinlichkewit 50% zerfallen ist. Im Durchnitt wird also zu diesem Zeitpunkt t̃ etwa die Hälfte
aller Isoptope im radioaktiven Gegenstand zerfallen und somit die Strahlung auf die Hälfte
abgesunken sein. In diesem Zusammenhang ist der Median einer exponentialverteilten Zufallsgrösse besser bekannt unter dem Begriff Halbwertszeit“.
”
Erste Aufgaben zur Standard-Normalverteilung
Aufgabe 70 ◦ :
Die zufällige Abweichung der Länge eines Werkstücks vom Sollmass ist normalverteilt mit
µ = 0 mm und σ = 1 mm. Stücke mit einer Abweichung, die zwischen −0.5 und +0.5
mm liegt, sind gut, solche mit einer Abweichung zwischen +0.5 und +1.5 mm werden
nachbearbeitet, der Rest ist Ausschuss.
a) Was bedeutet die Angabe µ = 0 mm konkret? Geben Sie eine kurze Antwort.
b) Welches sind die Wahrscheinlichkeiten der drei Sorten (gut, wird nachbearbeitet, Ausschuss)?
c) Zeichnen Sie den Graphen der Dichtefunktion der zugehörigen Normalverteilung. Wichtig sind: Symmetrie und Wendepunkte; tragen Sie auch die entsprechenden Punkte auf
3
der y-Achse ein, deren Massstab vernünftig zu wählen ist.
d) Stellen Sie in der Figur von c) die unter b) bestimmten Wahrscheinlichkeiten geometrisch dar. Verwenden Sie verschiedene Farben.
e) Verkauft werden die guten und die nachbearbeiteten Teile, nicht aber der Ausschuss.
Mit welcher Wahrscheinlichkeit ist ein verkauftes Werkstück nachbearbeitet worden?
Aufgabe 71 (4 Punkte):
Skizzieren Sie (im selben Koordinatensystem und mit verschiedenen Farben) die Graphen
(inkl. Extrema und Wendepunkte) der Dichtefunktion der folgenden Normalverteilungen:
a) N (2, 0.5), b) N (2, 1), c) N (−2, 1).
d) Überlegen Sie sich anhand der Skizzen, was der Median einer N (µ, σ 2 )-verteilten Zufallsgrösse ist. Sie brauchen den Median nicht zu formal zu berechnen, sondern nur eine
anschauliche Begündung zu geben!
Aufgabe 72 (3 Punkte):
Wie gross sind für eine N (0, 1)-verteilte Zufallsgrösse X die folgenden Wahrscheinlichkeiten (mit Hilfe einer Tabelle zu lösen): a) P[|X| ≤ 1], b) P[|X| ≤ 2.5] c), P[X > −1], d)
P[−0.1 ≤ X ≤ 0.3], e) P[−0.1 < X < 0.3].
Repetitionsaufgaben
Aufgabe 73 (3 Punkte):
Drei Kurzaufgaben:
a) Zu welcher Skala (Nominalskala etc.) gehören die folgenden beiden Merkmale: i) Startnummer einer Teilnehmerin an der SOLA-Staffette, ii) die von ihr erzielte Zeit?
b) Ein unverfälschter Würfel wird zehnmal geworfen. Mit welcher Wahrscheinlichkeit fällt
dabei höchstens zweimal eine Sechs?
c) Wir würfeln gleichzeitig mit zwei ausgewogenen Würfeln und betrachten die Ereignisse
E: Die Summe der Augenzahlen ist 6“ und F : Das Produkt der Augenzahlen ist 6“.
”
”
Untersuchen Sie die beiden Ereignisse auf Unabhängigkeit.
17. März 2008
4