5 Punkte - Fakultät Physik

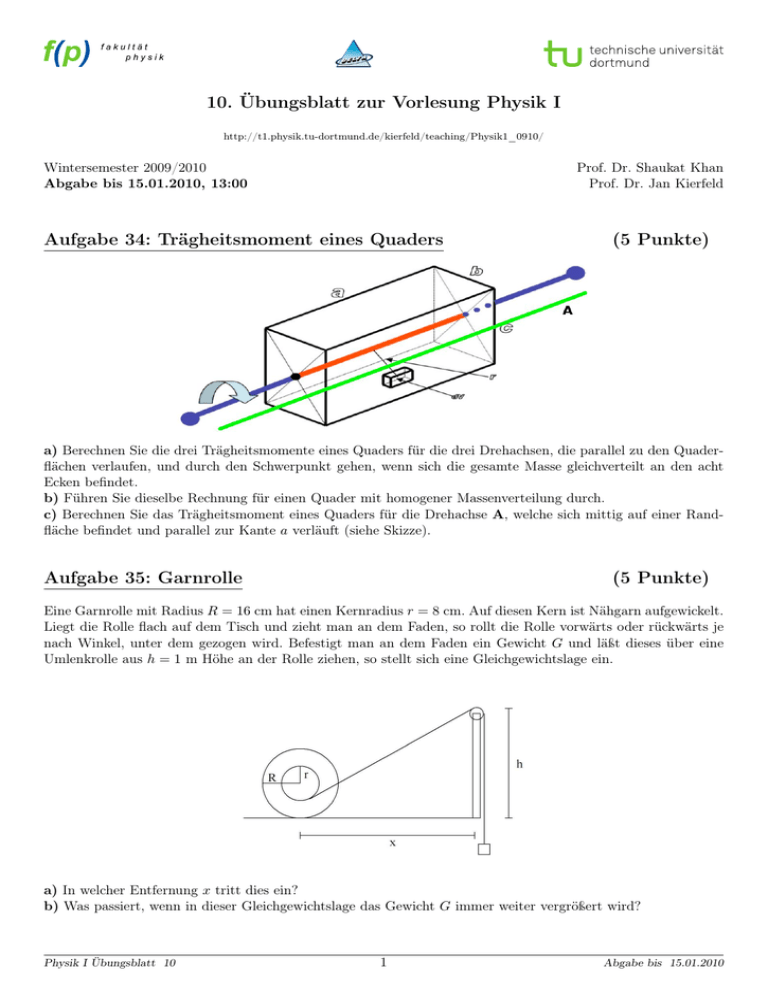
10. Übungsblatt zur Vorlesung Physik I
http://t1.physik.tu-dortmund.de/kierfeld/teaching/Physik1_0910/
Wintersemester 2009/2010
Abgabe bis 15.01.2010, 13:00
Prof. Dr. Shaukat Khan
Prof. Dr. Jan Kierfeld
Aufgabe 34:
Trägheitsmoment
eines
Aufgabe
XX: Trägheitsmoment
einesQuaders
Quaders
(5
(5 Punkte)
Punkte)
a) Berechnen a)
Sie
die dreiSieTrägheitsmomente
eines
Drehachsen,
parallel
zu den QuaderBerechnen
die drei Trägheitsmomente
einesQuaders
Quaders fürfür
die die
drei drei
Drehachsen,
die paralleldie
zu den
Quaderflächenund
verlaufen,
undden
durchSchwerpunkt
den Schwerpunktgehen,
gehen, wenn
sichsich
die gesammte
Masse gleichverteilt
an den acht an den acht
flächen verlaufen,
durch
wenn
die gesamte
Masse gleichverteilt
Ecken befindet.
Ecken befindet.
b) Führen Sie die selbe Rechnung für ein Quader mit homogener Massenverteilung durch.
b) Führen Siec)dieselbe
für einen eines
Quader
mitfürhomogener
durch.
BerechnenRechnung
Sie das Trägheitsmoment
Quaders
die Drehachse Massenverteilung
A.
c) Berechnen Sie das Trägheitsmoment eines Quaders für die Drehachse A, welche sich mittig auf einer Randfläche befindet und parallel zur Kante a verläuft (siehe Skizze).
Aufgabe 35: Garnrolle
(5 Punkte)
Eine Garnrolle mit Radius R = 16 cm hat einen Kernradius r = 8 cm. Auf diesen Kern ist Nähgarn aufgewickelt.
Liegt die Rolle flach auf dem Tisch und zieht man an dem Faden, so rollt die Rolle vorwärts oder rückwärts je
nach Winkel, unter dem gezogen wird. Befestigt man an dem Faden ein Gewicht G und läßt dieses über eine
Umlenkrolle aus h = 1 m Höhe an der Rolle ziehen, so stellt sich eine Gleichgewichtslage ein.
a) In welcher Entfernung x tritt dies ein?
b) Was passiert, wenn in dieser Gleichgewichtslage das Gewicht G immer weiter vergrößert wird?
Physik I Übungsblatt 0
Physik I Übungsblatt 10
1
1
Abgabe bis 00.00.0000
Abgabe bis 15.01.2010
Aufgabe 36: Little Green Men
(5 Punkte)
Der Krebsnebel im Sternbild Stier ist der Überrest einer Supernovaexplosion, die (nach der Expansion des
Nebels zu urteilen) vor ca. 900 Jahren stattgefunden haben muss. Tatsächlich berichten Quellen aus China,
Japan, Arabien und Europa von der Beobachtung eines „sehr hellen Sterns“ im Jahr 1054. Im Zentrum des
Nebels wurde 1969 ein Pulsar entdeckt, der regelmäßig mit einer Periode von T = 0,0331 s Radiopulse emittiert.
Derart regelmäßige Radioquellen schrieb man anfangs fremden Zivilisationen zu und katalogisierte sie als LGM
1, 2, ... („Little Green Men“, da Außerirdische bekanntlich klein und grün sind). Inzwischen glaubt man eher,
dass es sich um schnell rotierende Himmelskörper handelt.
a) Wie groß kann der Radius des Himmelskörpers sein, ohne dass die Umfangsgeschwindigkeit bei der angegebenen Periode die Lichtgeschwindigkeit erreicht?
b) Wie groß kann der Radius des Himmelskörpers sein, ohne dass sich Teile von seiner Oberfläche ablösen
(vermutete Masse = 1,4 Sonnenmassen; Sonnenmasse = 2,0 · 1030 kg)?
c) Da nach der Explosion des Himmelskörpers keine Kernprozesse mehr stattfinden, wird seine Rotation als
Energiequelle für die Abstrahlung des gesamten Nebels vermutet. Es wird beobachtet, dass T pro Jahr um
1,1 · 10−5 s zunimmt. Schreiben Sie die Rotationsenergie als Funktion von T . Durch Ableiten erhalten Sie die
Energieänderung als Funktion der Änderung dT /dt der Periode. Die Strahlungsleistung des Nebels läßt sich zu
5 · 1031 Watt abschätzen. Betrachten Sie den Himmelskörper als homogene Kugel mit der oben angegebenen
Masse und berechnen Sie seinen Radius.
d) Machen Sie mit einer kurzen Abschätzung plausibel, warum der Himmelskörper so schnell rotiert. Die Sonne
(Radius 7 · 108 m) braucht 25,4 Tage für eine Umdrehung (an ihrem Äquator, in höheren Breiten rotiert sie noch
langsamer).
e) Vergleichen Sie die Dichte, die sich aus der Masse in b) und dem Radius aus c) ergibt, mit der typischen Dichte von Kernmaterie (ein Neutron hat eine Ausdehung von etwa 1 fm = 10−15 m und eine Masse
von 940 MeV/c2 = 1,67 · 10−27 kg). Was kann man daraus schließen?
Aufgabe 37: Trapezkünstler
(5 Punkte)
Ein Trapezkünstler will bei einem 1,87 s dauernden Sprung in die Hände seines Partners einen vierfachen Salto
ausführen (siehe Abbildung). Für die erste und die letzte Vierteldrehung nimmt er eine gestreckte Haltung
mit dem Trägheitsmonent I1 = 19,9 kg m2 bezüglich seines Schwerpunkts ein. Während der restlichen Flugphase
winkelt er Beine und Arme so weit wie möglich an, sein Trägheitsmoment beträgt dann nur noch I2 = 3,93 kg m2 .
Wie groß muss die Winkelgeschwindigkeit ω2 des Artisten bezüglich seines Schwerpunkts in der gehockten Phase
sein, damit er sein Kunststück erfolgreich vorführen kann ?
Physik I Übungsblatt 10
2
Abgabe bis 15.01.2010