Kurs 7 – Geometrie 2 – MSA – Vollzeit (1 von 2)

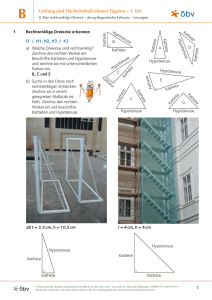
Erwachsenenschule Bremen
Abteilung I: Sekundarstufe
Doventorscontrescarpe 172 A
28195 Bremen
So schätze ich meinen Lernzuwachs ein. Kapitel
Ich …
1.
2.
3.
4.
5.
im Buch
kann die Hypotenuse, Ankathete und
Gegenkathete für einen Winkel des rechtwinkligen
Dreiecks finden.
… kann den Satz des Pythagoras in einem
rechtwinkligen Dreieck anwenden und fehlende
Seiten berechnen
… bin mit den Tasten für die trigonometrischen
Funktionen vertraut und kann sie bedienen.
… kenne entweder die trigonometrischen Funktionen
(sin, cos, tan) und kann sie an einem
rechtwinkligen Dreieck anwenden;
oder kenne den Sinussatz für allgemeine Dreiecke.
… kann beliebige Winkel und Seiten im
rechtwinkligen Dreieck berechnen.
6
6
7
7
7.
… erkenne beliebige Körper und ihre Eigenschaften
anhand ihrer Form aus verschiedenen
Perspektiven.
… kenne die Eigenschaften und die
Beschriftungsweise beliebiger Prismen.
8.
… kann die Netze beliebiger Prismen erkennen und
zeichnen. [siehe Kurs 3.30 und 3.31]
9
9.
… kann beliebige Prismen in der Parallelperspektive
erkennen und zeichnen. [siehe Kurs 3.30 und 3.31]
9
6.
10.
11.
… kann über die Oberflächenformel beliebiger
Prismen mit Hilfe der Äquivalenzumformung
fehlende Größen berechnen.
… kann über die Volumenformel beliebiger Prismen
mit Hilfe der Äquivalenzumformung fehlende
Größen berechnen.
9
9
9
9
muss ich lernen
Name:
kann ich sicher
Kurs 7 – Geometrie 2 – MSA – Vollzeit (1 von 2)
Datum
So schätze ich meinen Lernzuwachs ein. Kapitel
im Buch
Ich …
12.
… erkenne folgende spitze Körper: Pyramide, Kegel
9
13.
… kenne die Eigenschaften und Beschriftungsweisen
folgender spitzer Körper: Pyramide, Kegel
9
14.
… kann die Netze folgender spitzer Körper erkennen
und zeichnen: Pyramide, Kegel
9
17.
… kann über die Oberflächenformel spitzer Körper mit
Hilfe der Äquivalenzumformung fehlende Größen
berechnen.
… kann über die Volumenformel spitzer Körper mit
Hilfe der Äquivalenzumformung fehlende Größen
berechnen.
… kann Volumen und Oberfläche
zusammengesetzter Körper berechnen.
18.
… kann die Masse beliebiger Körper über die Dichte
und das Volumen berechnen.
9
19.
… kann Größen aus einem Textzusammenhang
entnehmen und damit rechnen.
9
15.
16.
9
9
9
muss ich lernen
Name:
kann ich sicher
Kurs 7 – Geometrie 2 – MSA – Vollzeit (2 von 2)
Datum
Übungen zur Selbstkontrolle – Mathematik Kurs 7
C. Nr.
7.01
7.02
7.03
Aufgaben
Bestimmen Sie die Hypotenuse (h),
die Ankathete (a) und
die Gegenkathete (k) von α .
Bestimmen Sie den Wert
der unbestimmten Kathete.
3 cm
↓?
12 cm
3 cm
α
Benennen Sie diese Objekte:
C. Nr.
7.01
α
Wie bekomme ich den Wert eines Winkels heraus, wenn ich das
Seitenverhältnis von Kathete/n und /oder Hypotenuse schon kenne?
7.04/05 Bestimmen Sie den Wert
der unbestimmten Kathete
(α = 20°) .
7.06
Datum
Lösungen
Bestimmen Sie die Hypotenuse (h),
die Ankathete (a) und
die Gegenkathete (k) von α .
k
h
α
a
7.02
7.03
Bestimmen Sie den Wert
der unbestimmten Kathete.
√(12² – 3²) ≈ 11,6
↓?
12 cm
Wie bekomme ich den Wert eines Winkels heraus, wenn ich das
Seitenverhältnis von Kathete/n und /oder Hypotenuse schon kenne?
Individuelle Lösung: In den meisten Fällen muss ich das Verhältnis eingeben
und die Umschalttaste des TR benutzen und dann entweder tan, sin oder cos
drücken.
7.04/05 Bestimmen Sie den Wert
der unbestimmten Kathete
(α = 20°) .
3 : (tan 20°) ≈ 8,2 cm
7.06
3 cm
3 cm
α
Benennen Sie diese Objekte:
Würfel
Zylinder
Quader
Zylinder
Dreiecksprisma
Übungen zur Selbstkontrolle – Mathematik Kurs 7
C. Nr.
Aufgaben
7.07
Bestimmen Sie die Art der Flächen aus der sich die Oberfläche eines
Zylinders, eines Würfels und eines Prismas mit einer regelmäßigen,
fünfeckigen Grundfläche zusammensetzt.
7.08
Was ist das?
7.09
Zeichnen Sie ein regelmäßiges,
6-eckiges Prisma in der Parallelperspektive: (Tipp: Benutzen Sie
kariertes Papier)
7.10
Bestimmen Sie die Seite a eines Quaders, wenn b = 5 cm, c= 8 cm
und O = 340 cm².
7.11
Bestimmen Sie die Seite a eines Würfels, wenn V = 2744 cm³.
C. Nr.
7.07
Datum
Lösungen
Bestimmen Sie die Art der Flächen aus der sich die Oberfläche eines
Zylinders, eines Würfels und eines Prismas mit einer regelmäßigen,
fünfeckigen Grundfläche zusammensetzt.
Zylinder: 2 gleichgroße Kreise und ein Rechteck
Würfel: 6 gleichgroße Quadrate
Fünfeckiges Prisma: 2 gleichgroße Fünfecke und 5 Rechtecke
7.08
Was ist das?
Das Netz von einem Quader
7.09
Zeichnen Sie ein regelmäßiges, 6-eckiges Prisma in der Parallelperspektive.
(Tipp: Benutzen Sie kariertes Papier)
Sie zeichnen einen Kreis und setzen den (unverstellten) Zirkel an einem beliebigen Punkt auf
dem Kreis an und markieren 2 Schnittpunkte, diese benutzen Sie um dort den Zirkel erneut
anzusetzen und markieren weitere Schnittpunkte. Das machen Sie solange bis Sie 6 Punkte
haben, die Sie miteinander verbinden. Nun zeichnen Sie von jeder Ecke je eine gleichlange
Strecke im Winkel 45° zur Blattkante. Jede Strecke soll in die gleiche Richtung zeigen. (jede
Strecke nur halb so lang wie sie in Wirklichkeit ist – perspektivische Verkürzung). Zuletzt
müssen die Enden der Strecken noch miteinander verbunden werden.
7.10
Bestimmen Sie die Seite a eines Quaders, wenn b = 5 cm, c= 8 cm und O =
340 cm².
340 = 2 ∙a∙5 + 2 ∙a∙8 + 2 ∙8∙5
340 = 26 ∙a + 80
260 = 26 ∙a → a = 10
7.11
Bestimmen Sie die Seite a eines Würfels, wenn V = 2744 cm³
2744⅓ = 14 cm
Übungen zur Selbstkontrolle – Mathematik Kurs 7
C. Nr.
Aufgaben
Datum
7.12
Benennen Sie diese Objekte:
7.13
Aus welchen Flächen setzt sich eine quadratische Pyramide
zusammen und warum gibt es 2 verschiedene Höhen in dieser
Pyramide?
7.14
Zeichnen Sie das Netz einer rechteckigen Pyramide.
(Tipp: Benutzen Sie kariertes Papier)
7.15
Bestimmen Sie den Mantelradius s eines Kegels, wenn r = 5 cm und
O = 188,5 cm².
7.16
Bestimmen Sie die den Radius r eines Kegels, wenn V = 37,7 cm³.
C. Nr.
7.12
Lösungen
Benennen Sie diese Objekte:
Pyramide
7.13
Kegel
Aus welchen Flächen setzt sich eine quadratische Pyramide zusammen und
warum gibt es 2 verschiedene Höhen in dieser Pyramide?
4 gleichgroße, gleichschenklige Dreiecke und ein Quadrat. Es gibt eine Höhe
im Dreieck des Mantels und eine Körperhöhe.
7.14
Zeichnen Sie das Netz einer rechteckigen Pyramide.
(Tipp: Benutzen Sie kariertes Papier)
Die Schenkel der Dreiecke
müssen alle gleichlang sein!
7.15
Bestimmen Sie den Mantelradius s eines Kegels, wenn r = 5 cm und O = 188,5
cm².
188,5 = π ∙ 5² + π ∙ 5 ∙ s
(188,5 - π ∙ 5²) : π : 5 ≈ 7 cm
7.16
Bestimmen Sie die den Radius r eines Kegels, wenn V = 37,7 cm³.
37,7 = π ∙ r² : 3
√(37,7 ∙ 3 : π) ≈ 6 cm
Übungen zur Selbstkontrolle – Mathematik Kurs 7
C. Nr.
Aufgaben
7.17
Berechnen Sie die Oberfläche
und das Volumen dieses Körpers.
Der obere und der untere Teil haben
jeweil seinen Radius von 4 cm und
eine Höhe von 9 cm.Der mittlere Teil
hat eine Länge von 80 mm,
eine Breite von 70 mm und
eine Höhe von 90 mm.
7.18
Berechnen Sie das Gewicht eines Kegels mit einem Volumen von
300 cm³ und einer Dichte von 7,2 g/cm³.
7.19
Ein runder Kirchturm mit einem 8 m Durchmesser ist 30 m hoch und
hat ein 5 m hohe, kegelförmige Spitze. Wie groß ist die Mauerfläche
und wie groß ist die Dachfläche?
C. Nr.
7.17
Datum
Lösungen
Berechnen Sie die Oberfläche
und das Volumen dieses Körpers.
Der obere und der untere Teil haben
jeweil seinen Radius von 4 cm und
eine Höhe von 9 cm.Der mittlere Teil
hat eine Länge von 80 mm,
eine Breite von 70 mm und
eine Höhe von 90 mm.
O= 2 Rechtecke + 2 Rechtecke + 2 Rechtecke + 2 Rechtecke
O= 2 ∙ 2 ∙ π ∙ 4 ∙ 9 + 2 ∙ 8 ∙ 7
+ 2∙8∙9
+2∙9∙7
≈ 834 cm²
V= 2 Zylinder + 1 Quader
V= 2 ∙ 9 ∙ π ∙ 4² + 7 ∙ 8 ∙ 9 ≈ 1409 cm³
7.18
Berechnen Sie das Gewicht eines Kegels mit einem Volumen von 300 cm³ und
einer Dichte von 7,2 g/cm³.
M = 300 ∙ 7,2 = 2160 g
7.19
Ein runder Kirchturm mit einem 8 m Durchmesser ist 30 m hoch und hat ein 5
m hohe, kegelförmige Spitze. Wie groß ist die Mauerfläche und wie groß ist die
Dachfläche?
Mauerfläche: A= 2 ∙ π ∙ 4 ∙ 30 ≈ 754 m²
Dachfläche: A= √(5²+4²) ∙ π ∙ 4 ≈ 80,5 m²