x - NiBiS

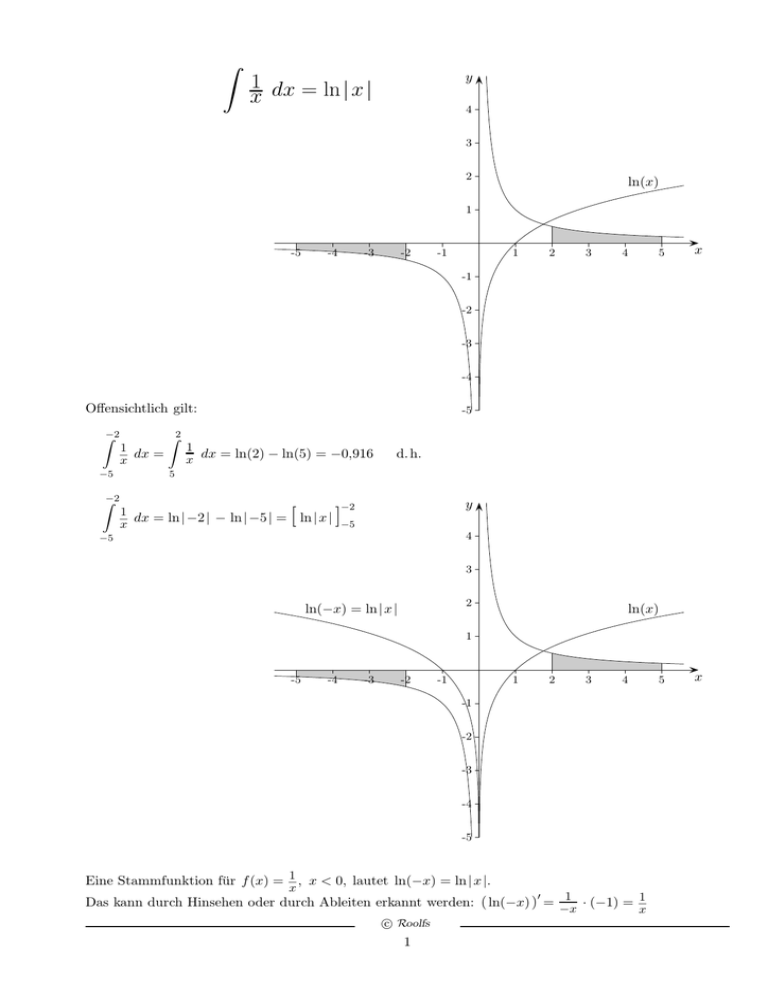
Z
y
1
x dx = ln | x |
4
3
2
ln(x)
1
-5
-4
-3
-2
-1
1
2
3
4
5
x
-1
-2
-3
-4
Offensichtlich gilt:
Z−2
Z2
−5
5
1
− dx =
x
Z−2
-5
1
x dx = ln(2) − ln(5) = −0,916
1
− dx = ln | −2 | − ln | −5 | =
x
d. h.
y
−2
[ ln | x | ]−5
4
−5
3
2
ln(−x) = ln | x |
ln(x)
1
-5
-4
-3
-2
-1
1
2
3
4
-1
-2
-3
-4
-5
1 , x < 0, lautet ln(−x) = ln | x |.
Eine Stammfunktion für f (x) = −
x
1
1
Das kann durch Hinsehen oder durch Ableiten erkannt werden: ( ln(−x) ) = −x · (−1) = −
x
′
c Roolfs
1
5
x
Zur Erinnerung:
1
(ln x)′ = −
x
(x > 0)
Begründung:
e ln x = x | ( )′
(Kettenregel)
e ln x (ln x)′ = 1
1
(ln x)′ = −
x
y
4
3
2
ln(−x) = ln | x |
ln(x)
1
-5
-4
-3
-2
-1
1
2
3
4
5
-1
-2
-3
-4
-5
Man beachte die Symmetrie. Aus der y-Achsensymmetrie F (x) = F (−x) folgt für die Ableitung
die Punktsymmetrie F ′ (x) = −F ′ (−x) (Kettenregel).
c Roolfs
2
x