n-1 n+1 n n+2 n+3 n+4 un a

K
un-1
un
un+1 un+2 un+3 un+4
a
n-1
n
n+1
n+2
n+3
n+4
4.2.3 Das zweiatomige Gitter
Als nächstes betrachten wir die eindimensionale Kette mit zwei-atomarer Basis. Hierbei gibt
es prinzipiell folgende mögliche Unterschiede:
1. die Wechselwirkung zwischen den Atomen alterniert bei gleicher Masse der Atome
a
C1
d
C2
2. die Masse der beiden Atome ist unterschiedlich
a
C
M1
M2
3. Wechselwirkung alterniert bei unterschiedlichen Massen
101
Wir werden den ersten der aufgezählten Fälle etwas genauer diskutieren.
Die Periode des Gitters sei wieder mit a bezeichnet. Der Abstand zwischen den zwei
Atomen der Basis sei d mit d ≤ a/2. somit hängt die Kraft davon ab ob der Abstand d oder
a − d ist. Es werden wieder nur Nächstenachbar-Wechselwirkungen berücksichtigt. So ergibt
sich für die harmonische potentielle Energie:
harm
Epot
=
C1 X
C2 X
[u1 (na) − u2 (na)]2 +
[u2 (na) − u1 ((n + 1)a)]2 .
2 n
2 n
(4.27)
Dabei bezeichnet u1 die Verschiebung des an Position na befindlichen Atoms und u2 die des
Atoms an Position na + d. Es sei o.E.d.A. C1 ≥ C2 . Für die Bewegungsgleichungen ergibt
sich dann:
harm
∂Epot
∂u1 (na)
= −C1 [u1 (na) − u2 (na)]
M u¨1 (na) = −
−C2 [u1 (na) − u2 ({n − 1}a)]
M u¨2 (na) = −
harm
∂Epot
∂u2 (na)
= −C1 [u2 (na) − u1 (na)]
−C2 [u2 (na) − u1 ({n + 1}a)]
(4.28)
Wir suchen wieder Lösungen mit dem Ansatz:
u1 (na, t) = 1 ei(Kna−ωt)
u2 (na, t) = 2 ei(Kna−ωt)
(4.29)
Dabei sind 1 und 2 Konstanten die das Amplitudenverhältnis und die relative Phase festlegen. Eingesetzt in die DGL:Wir benutzen wieder die Born-von Karman Randbedingungen,
wie im einatomaren Fall und somit ergeben sich auch hier N Werte für K. Setzen wir nun
den Lösungsansatz Gl.(4.29) in die DGL Gl.(4.28) ein, so erhalten wir:
− M ω 2 1 ei(Kna−ωt) = −C1 [1 ei(Kna−ωt) − 2 ei(Kna−ωt) ]
−C2 [1 ei(Kna−ωt) − 2 ei(K(n−1)a−ωt) ]
−M ω 2 2 ei(Kna−ωt) = −C1 [2 ei(Kna−ωt) − 1 ei(Kna−ωt) ]
−C2 [2 ei(Kna−ωt) − 1 ei(K(n+1)a−ωt) ]
(4.30)
mit 2 ei(K(n−1)a−ωt) = 2 ei(Kna−ωt) e−iKa , 1 ei(K(n+1)a−ωt) = 1 ei(Kna−ωt) eiKa und nach
Dividieren durch e(iKa−ωt) ergibt sich:
− M ω 2 1 = −C1 [1 − 2 ] − C2 [1 − 2 e−iKa ]
−M ω 2 2 = −C1 [2 − 1 ] − C2 [2 − 1 eiKa ]
102
(4.31)
Durch Zusammenfassen nach 1 und 2 folgt:
[M ω 2 − (C1 + C2 )]1 + (C1 + C2 e−iKa )2 = 0
(C1 + C2 eiKa )1 + [M ω 2 − (C1 + C2 )]2 = 0.
(4.32)
Die DGL besitzt eine Lösung, wenn die Determinate der Koeffizientenmatrix verschwindet:
[M ω 2 − (C1 + C2 )]
(C1 + C2 e−iKa ) =0
(4.33)
(C1 + C2 eiKa )
[M ω 2 − (C1 + C2 )] Somit ergibt sich:
[M ω 2 − (C1 + C2 )]2 = |C1 + C2 e−iKa |2 = C12 + C22 + 2C1 C2 cos(Ka)
Die Dispersionsrelation für den zweiatomigen Fall lautet dann:
q
C1 + C2
1
ω2 =
±
C12 + C22 + 2C1 C2 cos(Ka)
M
M
wobei für das Amplitudenverhältnis gelten muss:
(4.34)
(4.35)
2
C1 + C2 eiKa
=∓
1
|C1 + C2 eiKa |
(4.36)
Wie aus der Dispersionsrelation zu erkennen ist, existieren für jeden K-Wert zwei Lösungen,
was durch den zusätzlichen inneren Freiheitsgrad der Basis verständlich ist. Das gesamte
System besitzt also 2N Freiheitsgrade.
1/2
(2(C1+C2)/M)
1/2
(2C1/M)
1/2
(2C2/M)
hier existieren keine stat. Lösungen
-1
0
K/(π/a)
1
2
Den unteren Ast bezeichnet man als akustischen Zweig, da er bei kleinen K-Werten die
gleiche Dispersionsrelation wie akustische Wellen aufweist (ω = cK). Den oberen Ast bezeichnet man als optischen Zweig, da sich die langwelligen Moden (kleine K-Werte) optisch
anregen lassen und sie die optischen Eigenschaften der Kristalle bestimmen.
Wir betrachten zwei Spezialfälle:
103
1. Fall K π/a: Hier gilt: cos(Ka) ≈ 1 − (Ka)2 /2. Damit ergeben sich die Lösungen aus
der Dispersionsrelation:
r
2(C1 + C2 )
ω1 =
− O(Ka)2 ,
(4.37)
M
s
ω2 =
C1 C2
(Ka)
2M (C1 + C2 )
(4.38)
So ergeben sich für den langwellig akustischen Zweig folgende Schwingungskonfiguration:
und langwellig optischen Zweig:
2. Fall K = π/a: Für diesen Fall ist cos(Ka) = −1 und somit ergeben sich die folgenden
Lösungen:
r
2C1
, mit 1 = −2
(4.39)
ω1 =
M
r
2C2
ω2 =
, mit 1 = 2
(4.40)
M
Hier resultieren für den kurzwellig akustischen Zweig folgende Schwingungskonfiguration:
und den kurzwellig optischen Zweig:
104
4.2.3.1 Transversale Phononen
Transversale akustische Phononen
+ - +
+
+
+
+
+
- + - + Transversale optische Phononen
+
+
-
-
-
-
+ +
+
+
+
+
+
-
-
-
Hier ist eine Darstellung zur Verdeutlichung des Unterschieds zwischen transversal akustischen und transversal optischen Phononen zu sehen. Es wird deutlich, dass sich bei den
transversal optische Phononen zeitlich ändernde Dipolmomente ausbilden, über die das Phononensystem mit elektromagnetischer Strahlung wechselwirken kann.
105
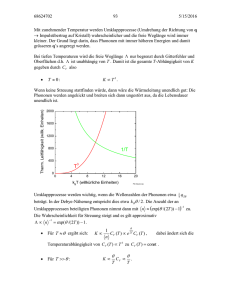
4.2.3.2 Phononen in drei Dimensionen
(a) Hier sind experimentellen Ergebnisse
dargestellt, die an einem Silizium-Einkristall
gemessen wurden und einer Modellrechnung
gegenüber gestellt sind. An den Achsen ist
nicht die Wellenzahl K sondern die reduzierte Wellenzahl ζ = Ka/2π aufgetragen. Die Bezeichnungen im Diagramm stehen für: TA transversal akustisch, TO transversal optisch, LA longitudinal akustisch und
LO longitudinal optisch. (b) Zu den Messungen aus Teil (a) sind zwei Brillouin-Zonen
und die entsprechenden Pfade eingezeichnet, entlang derer gemessen wurde.
4.2.4 Quantisierung einer elastischen Welle
Die Energie eines elastischen Schwingungszustandes ist gegeben als:
1
E = n+
~ω
2
(4.41)
wobei 21 ~ω die Nullpunktsenergie ist. Wir betrachten im Folgenden das mittlere Amplitudenquadrat der Phononen. Die Auslenkung lässt sich schreiben:
u(x, t) = u0 cos(Kx) cos(ωt)
(4.42)
Die mittlere Energie teilt sich, wie in jedem harmonischen Oszillator, zur Hälfte auf die kinetische und zur Hälfte in die potentielle Energie auf. Die Energiedichte lässt sich mit Hilfe der
2
Massendichte ρ durch 21 ρ ∂u
angeben. Nach Integration über das gesamte Kristallvolumen
∂t
erhält man:
1
Ekin = ρV ω 2 u20 sin2 (ωt)
(4.43)
4
106
und somit für die zeitgemittelte Energiedichte der kinetischen Energie:
1
1
1
n+
~ω
ρV ω 2 u20 =
8
2
2
(4.44)
aufgelöst nach dem Amplitudenquadrat u20 ergibt:
4 n + 12 ~
=
.
(4.45)
ρV ω
Auf diese Weise lässt sich eine Auslenkung mit einer Phononenbesetzungszahl verknüpfen.
u20
4.2.5 Der Impuls eines Phonons
~ besitzen würden, wie sich aus
Die Phononen verhalten sich, als ob sie einen Impuls von ~K
Streuexperimenten mit Neutronen, Elektronen und Photonen ergibt. Wir zeigen im Folgenden, dass Phononen keinen physikalischen Impuls besitzen außer im Fall K = 0. Der gesamte
Impuls berechnet sich mit:
d X
p=M
un
(4.46)
dt n
Ist ein Phonon K im Kristall mit einer Anzahl von N Atomen angeregt so gilt:
du X inKa
p=M
e
dt n
mit
N
−1
X
xn =
n=0
1 − xN
1−x
(4.47)
(4.48)
ergibt sich:
du 1 − eiN Ka
(4.49)
dt 1 − eiKa
Da der Wellenvektor nur diskrete Werte K = ±2πr/N a (mit der ganzen Zahl r) annehmen
kann, ergibt sich für eiN Ka = e±i2πr = 1, weshalb die rechte Seite von Gl.(4.49) Null wird:
du X inKa
du 1 − 1
p=M
e
=M
=0
(4.50)
dt n
dt 1 − eiKa
p=M
~ wird als Kristallimpuls bezeichnet.
Die Größe ~K
Bei der elastischen Streuung von Röntgenstrahlung haben wir gesehen, dass ein Röntgen~ wobei G
~ ein Vektor des reziproken Gitters
reflex bei Erfüllung der Bedingung ~k 0 = ~k + G,
~
ist. Dabei wird der Impuls −~G auf das Gitter als Ganzes übertragen. Dieser ist aber schwer
nachzuweisen, da hier natürlich die gesamte Masse des Kristalls eingeht oder aber gar der
Apparatur, falls der Kristall starr mit dieser verbunden ist.
~ bei der Streuung erzeugt, gilt folgende Gleichung:
Wird ein Phonon mit K
~k 0 + K
~ = ~k + G.
~
(4.51)
Wird hingegen ein Phonon bei der Streuung absorbiert gilt:
~k 0 = ~k + G
~ + K.
~
107
(4.52)
4.3 Der phononische Anteil an der spezifischen Wärme
Der phononischen Anteil der Wärmekapazität wird als Gitteranteil der Wärmekapazität
CV = (∂U/∂T )V (U ist die Energie, T die Temperatur) bezeichnet Clat . Die gesamte
Energie, die das Phononensystem bei einer bestimmten Temperatur T aufnimmt, lässt sich
durch die Energiesumme über alle Phononenzustände ausdrücken, welche durch die Polarisationszustand p (Ast in der Dispersionsrelation) und die verschiedenen Wellenzahlen K
gegeben sind. Somit ergibt sich für die Gesamtenergie:
U=
XX
K
UK,p =
p
XX
K
hnK,p i~ωK,p .
(4.53)
p
Dabei bezeichnet hnK,p i die Besetzungszahl des durch K und p charakterisierten Zustand
im thermischen Gleichgewicht. Da es sich bei Phononen um Bosonen handelt, verwenden wir
die Planck-Verteilung:
1
hnK,p i = ~ω
(4.54)
e kB T − 1
n
Die folgende Abbildung zeigt die Zunahme der angeregten Zustände mit steigender Temperatur:
4.5
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
-0.5
0
1
2
x=kBT/Xω
3
4
Das Verhältnis der Zahl von thermisch angeregten Oszillatoren im Quantenzustand (n + 1)
zu der im Zustand n entspricht dem Boltzmann-Faktor:
Nn+1
− ~ω
= e kB T
Nn
(4.55)
Betrachtet man die Anzahl der im Zustand n befindlichen Oszillatoren im Verhältnis zu allen
angeregten Oszillatoren so ergibt sich:
e−n~ω/kB T
= P∞ −s~ω/k T
B
s=0 Ns
s=0 e
N
P∞ n
108
(4.56)
Es ergibt sich damit für die im Mittel angeregten Zustände:
P
se−s~ω/kB T
hni = Ps −s~ω/k T
B
se
(4.57)
Zähler und Nenner der rechten Seite lassen sich mit:
X
X
1
d X s
x
xs =
sxs = x
x =
,
1
−
x
dx
(1
−
x)2
s
s
s
(4.58)
umschreiben. Setzt man x = e−~ω/kB T folgt aus Gl.(4.56):
P
sxs
x(1 − x)
hni = Ps s =
(1 − x)2
sx
=
x
e−~ω/kB T
=
(1 − x)
1 − e−~ω/kB T
=
1
e~ω/kB T
−1
(4.59)
4.3.1 Abzählen der Eigenschwingungen
Setzt man nun die Planck-Verteilung in die Gl.(4.53) ein so, ergibt sich für die Energie des
Phononensystems:
XX
~ωK,p
U=
.
(4.60)
~ω
/kB T − 1
K,p
e
p
K
Etwas allgemeiner lässt sich die Summe durch ein Integral ersetzen, wobei die Zustandsdichte
der Phononen mit einer bestimmten Polarisation p mit Dp (ω) bezeichnet ist:
XZ
~ω
U=
Dp (ω) ~ω/k T
dω.
(4.61)
B
e
−1
p
Die spezifische Wärmekapazität erhält man durch Differenzieren ∂U
∂T der Energie nach der
Temperatur:
2
~ω
Z
e~ω/kB T
X
kB T
∂U
= kB
dω.
(4.62)
Clat =
Dp (ω) ~ω/k T
B
∂T
(e
− 1)2
p
Die Schwierigkeit bei der Auswertung dieser Gleichung besteht in der Bestimmung der Zustandsdichte Dp (ω).
4.3.1.1 Die Zustandsdichte im Eindimensionalen
Festgehalten
L
n=0
un
a
109
n=14
Wir betrachten eine Kette aus N + 1 Atomen mit dem Abstand a und der Länge L.
Werden die beiden äußeren Atome festgehalten, ergeben sich nur stehende Wellen für die
Auslenkungen un der Atome als Lösungen:
un = u0 e−iωK,p t sin(nKa)
(4.63)
dabei ist ωK,p für eine bestimmte Polarisation p mit über die entsprechende Dispersionsrelation mit K verbunden. Durch die Randbedingung ergeben sich nur bestimmte Werte für die
Wellenzahl K:
K=
π 2π 3π 4π
(N − 1)π
, , , ,...,
L L L L
L
(4.64)
Betrachten wir nun die beiden extremen K-Werte. Es ergibt sich für den minimalen K-Wert,
π
K=L
, die Lösung:
nπa un ∝ sin
,
(4.65)
L
welche die Forderung erfüllt, dass u0 = 0 und uN = 0 ist. Für den maximalen Wert von
K = NLπ = Kmax ergibt sich
un ∝ sin(nπ).
(4.66)
Hier stehen alle Atome still, da sie alle auf den Knoten liegen. Somit ergeben sich N − 1
erlaubte verschiedene Werte für K. Alle K-Werte dazwischen besitzen den selben Abstand
∆K = π/L. Damit lässt sich eine Zustandsdichte pro Wellenzahl K von L/π für K ≤ π/a
und 0 für K > π/a angeben. Berücksichtigen wir die unterschiedlichen Polarisationen im
Eindimensionalen so ergeben sich für jede Wellenzahl drei Polarisationen (eine longitudinal
und zwei transversal).
Wir wollen die Zustandsdichte D(ω) auf ein Frequenzintervall von Eins beziehen. Somit
ergibt sich für die Anzahl der Zustände im Interval dω um die Frequenz ω:
D(ω)dω =
L dK
L dω
dω = dω
π dω
π dK
(4.67)
dω
dabei bezeichnet dK
die Gruppengeschwindigkeit, welche der Dispersionsrelation entnommen
werden kann. Daraus folgt, dass die Zustandsdichte immer dann eine Singularität aufweist,
wenn die Gruppengeschwindigkeit verschwindet, wenn also die Dispersionsrelation ω(K) eine
horizontale Tangente aufweist.
interessante physikalische Effekte auftreten, wie z.B. die Peierls-Instabilität
bei eindimensionalen Metallen.
110
4.3.1.2 Die Zustandsdichte im Dreidimensionalen
Ky
p/a
Kx
K
Die Argumentation verläuft analog zum Eindimensionalen. Wir betrachten periodische
Randbedingungen aus N 3 Einheitszellen eines kubischen Gitters mit der Kantenlänge L.
~
Damit gilt für K:
ei(Kx x+Ky y+Kz z) = ei(Kx (x+L)+Ky (y+L)+Kz (z+L)) .
(4.68)
So ergeben sich die folgenden möglichen Werte für die einzelnen Komponenten von K:
Nπ
2π 4π
,± ,...,±
(4.69)
L
L
L
~ in einem Volumen 2π 3 im K-Raum. Oder anders
Somit ergibt sich genau ein Wert von K
L
ausgedrückt:
3
L
V
= 3
(4.70)
2π
8π
Kx , Ky , Kz = 0, ±
erlaubte K-Werte pro Einheitsvolumen im K-Raum (L3 =V). Auch hier muss die Zahl noch
mit den verschiedenen Polarisationen multipliziert werden.
~ zu bestimmen, wird
Um die Gesamtzahl der Zustände mit einer Wellenzahl kleiner als |K|
die Anzahl der Zustände pro Einheitsvolumen Gl.(4.70) mit dem Volumen einer Kugel mit
Radius K multipliziert:
3
4πK 3
L
N=
(4.71)
2π
3
111
wieder für jede Polarisation. Somit beträgt die Zustandsdichte für jede Polarisation:
D(ω) =
dN
V K 2 dK
=
dω
2π 2 dω
(4.72)
4.3.1.3 Das Debye-Modell der Zustandsdichte
Vereinfachende Annahmen bei niedrigen Temperaturen:
1. Bei der Betrachtung bei niedrigen Temperaturen können die optischen Moden auch bei
Kristallen die eine mehratomige Basis besitzen vernachlässigt werden, da ihre Frequenz
nach unten begrenzt ist und somit nicht angeregt werden.
~ der drei akustischen Zweige durch die Form
2. Es ist möglich die Dispersionsrelation ω(K)
bei großen Wellenlängen annähern ω = cK. Dies ist korrekt, wenn kB T /~ deutlich
kleiner ist als die Frequenzen, bei denen eine Abweichung von dem linearen Verhalten
auftritt.
3. Das Integral über die erste Brillouin-Zone kann durch ein Integral über den gesamten
k-Raum angenähert werden. Die Näherung ist gut, da der Integrand nur dann nicht
vernachlässigbar klein ist, wenn ~cK die Größenordnung von kB T hat — was nur in
der Nähe von K = 0 bei niedrigen Temperaturen der Fall ist.
Wie oben unter Punkt 2 erwähnt, nehmen wir eine lineare Dispersionsrelation wie bei
kontinuierlichen Medien an:
ω = vK,
(4.73)
wobei v die Schallgeschwindigkeit in dem Medium ist. Somit ergibt sich für die Zustandsdichte nach Gl.(4.72):
V ω2
D(ω) = 2 3
(4.74)
2π v
Sind andererseits N Elementarzellen in der Probe vorhanden, so ist die Gesamtzahl der akustischen Phononenzustände ebenfalls N . Daraus kann mit Gl.(4.71) eine maximale Wellenzahl
KD angegeben werden, die man in der Probe antreffen kann:
r
2
3 6π N
KD =
(4.75)
V
und mit dem Zusammenhang ω = vK ergibt sich auch eine maximale Frequenz:
r
2 3
3 6π v N
ωD =
.
V
(4.76)
Somit sind im Debye-Modell keine Schwingungszustände mit K > KD zugelassen. Die
Anzahl der Zustände mit K ≤ KD entspricht der des einatomigen Gitters. Die Thermische
Energie U ergibt sich nach Gl.(4.61) für jede Polarisation zu:
Z
Z ωD ~ω
V ω2
U = D(ω)hn(ω)i~ωdω =
dω.
(4.77)
2π 2 v 3
e~ω/kB T − 1
0
112
Wird vereinfachend angenommen, dass alle Ausbreitungsgeschwindigkeiten der unterschiedlichen Polarisationen gleich sind ergibt sich einfach der Faktor drei für alle Polarisationen.
Somit erhält man:
3V ~
U= 2 3
2π v
Z
0
ωD
ω3
e~ω/kB T − 1
4 T4
3V kB
dω =
2π 2 v 3 ~3
Z
0
xD
x3
dx.
ex − 1
(4.78)
mit x = ~ω/kB T und xD = ~ωD /kB T = θ/T . Die Größe θ = ~ωD /kB wird als DebyeTemperatur bezeichnet. Sie lässt sich auch wie folgt ausdrücken:
~v
θ=
kB
r
3
6π 2 N
.
V
(4.79)
So dass sich damit für die Phononenenergie ergibt:
3 Z xD
T
x3
U = 9N kB T
dx.
θ
ex − 1
0
(4.80)
Die spezifische Wärmekapazität erhält man durch differenzieren der Gl.(4.78):
3V ~
Cv = 2 3
2π v kB T 2
Z
0
ωD
!
ω 4 e~ω/kB T
e~ω/kB T − 1
2
3 Z xD
T
x4 ex
dω = 9N kB
dx. (4.81)
θ
(ex − 1)2
0
Spezifische Wärmekapazität berechnet nach dem Debye-Modell
Für Werte T θ erreicht die Wärmekapazität ihren klassischen Wert 3N kB (Dulong-Petit).
113
Experimentell bestimmte spezifische Wärmekapazität für Silizium und Germanium
4.3.1.4 Debyesches T 3 -Gesetz
Bei tiefen Temperaturen kann die Phononenenergie aus Gl.(4.80) nähern, dabei wird die
Integration bis ωD durch eine Integration bis unendlich genähert:
Z
0
xD
x3
dx ≈
ex − 1
Z
∞
0
x3
dx =
ex − 1
∞
Z
3
x
0
∞
X
−nx
e
n=1
∞
X
1
π4
dx = 6
=
.
n4
15
(4.82)
n=1
Somit gilt im Falle T θ:
U'
3π 4 N kB T 4
5θ3
(4.83)
und somit ergibt sich für die spezifische Wärmekapazität:
12π 4
Cv '
5
3
3
T
T
N kB ' 234N kB
θ
θ
(4.84)
Dies wird als Debyesche T 3 -Näherung bezeichnet.
Experimentell bestimmte spezifische Wärmekapazität für Argon bei tiefen Temperaturen
114
Für Argon ist θ =92K. Für die meisten Stoffe gibt es nur bis zu eine Temperatur von
T < θ/50 eine gut Übereinstimmung mit dem Debyeschen T 3 -Gesetz.
Anschaulich verstehen lässt sich das Debyeschen T 3 -Gesetz mit folgendem Bild:
Ky
KD
Kx
KT
115
Bei niedrigen Temperaturen ist der K-Raum nur zu einem Bruchteil von ca. (ωT /ωD )3 bzw.
(KT /KD )3 gefüllt, deshalb können die angeregten Zustände mit annähernd T 3 zunehmen.
4.3.1.5 Das Einstein-Modell der Zustandsdichte
In Einsteins Näherung (1907) trägt jeder optische Zweig mit einer festen Anzahl N an
Zuständen bei. Es ergibt sich für die Energie der Phononen:
N ~ω
U = N hni~ω =
e~ω/kB T
−1
.
(4.85)
Damit ergibt sich für die Wärmekapazität nach Einstein:
CV =
∂U
∂T
= N kB
V
~ω
kB T
2
e~ω/kB T
.
(e~ω/kB T − 1)2
(4.86)
Bei hohen Temperaturen nimmt die Spezifische Wärmekapazität einen konstanten Wert
3N kB an. Bei tiefen Temperaturen fällt sie allerdings mit e−~ω/kB T . Dies widerspricht dem
Experimentell beobachteten T 3 -Gesetz.
Vergleich der Zustandsdichten nach dem Debye-Modell (a) und der eines
tatsächlichen Kristalls (b)
116
Werte der Debye-Temperatur und die Wärmeleitzahl für einige Elemente
I
II
III
IV
V
VI
VII
H
Li
344
0,85
Na
158
1,41
K
91
0,58
Rb
56
0,58
Cs
38
0,36
Fr
VIII
He
Be
1440
2,00
Mg
400
1,56
Ca
Sc
230 360
0,16
Sr
Y
147 280
0,17
Ba
Laβ
110 142
0,14
Ra
Ac
B
Debye-Temperatur θ/K
Wärmeleitzahl
Ti
420
0,22
Zr
291
0,23
Hf
252
0,23
V
380
0,31
Nb
275
0,54
Ta
240
0,58
Cr
630
0,94
Mo
450
1,38
W
400
1,74
Mn
410
0,08
Tc
0,51
Re
430
0,48
Fe
470
0,80
Ru
600
1,17
Os
500
0,88
Co
445
1,00
Rh
480
1,50
Ir
420
1,47
Ni
450
0,91
Pd
274
0,72
Pt
240
0,72
Cu
343
4,01
Ag
225
4,29
Au
165
3,17
Zn
327
1,16
Cd
209
0,97
Hg
71,9
0,27
Al
428
2,37
Ga
320
0,41
In
108
0,82
Tl
78,5
0,46
C
2230
1,29
Si
645
1,48
Ge
374
0,60
Snw
200
0,67
Pb
105
0,35
N
O
F
Ne
75
P
S
Cl
Ar
92
As
282
0,50
Sb
211
0,24
Bi
119
0,08
Se
90
0,02
Te
153
0,02
Po
Br
Kr
72
I
Xe
64
At
Rn
4.3.1.6 Vergleich zwischen Phononen und Photonen
Was muss geändert werden, wenn man von Phononen zu Photonen übergeht?
117
1. Die Schallgeschwindigkeit muss durch die Lichtgeschwindigkeit ersetzt werden.
2. Die Formel für die Energiedichte der Schwarzkörperstrahlung enthält den Faktor 2/3
gegenüber der für Phononen, da ein Photonen-Spektrum nur zwei transversale und
keinen longitudinale Mode aufweist (elektromagnetische Strahlung).
3. Die obere Grenze des bestimmten Integrals ist nicht ωD sondern unendlich, da es keine
Beschränkung der Frequenz für Photonen gibt.
Der Vergleich im Detail:
Anzahl der
schwingungen
Normal-
Beschränkung des Wellenvektors
Thermische Energiedichte
Phononen
~ ω = ωs (K)
~
3p Moden für jedes K
Photonen
zwei Moden für jedes ~k ω = ck
(c = 3 · 108 m/s)
~ auf die erste Brillouin-Zone beK
schränkt
P R π/a 1
~
~ωs (K)
~
dK
~
s 0
(2π)3 β~ωs (K)
~k unbeschränkt (beliebig)
−1
e
2
R∞
0
~ck
1
dk
(2π)3 eβ~ck −1
4.4 Streuung an zeitlich veränderlichen Strukturen —
Phononen-Spektroskopie
Zur Betrachtung der Streuung von Wellen an Phononen gehen wir von Gl.(2.22) auf Seite
41 aus:
Z
~
~ t) ∝ e−iω0 t ρ(~r)ei~r(t)·K
AB (B,
d~r
(4.87)
Um die Betrachtung
Peinfach zu halten, gehen wir von einer einatomigen Basis mit δ-artigen
Streuern ρ(~r, t) ∝ n δ(~r − ~rn (t)) aus:
X
~
~ t) ∝ e−iω0 t
AB (B,
ei~rn (t)·K .
(4.88)
Nun lässt sich der zeitabhängig Ort des Streuers ~rn (t) durch den Gittervektor ~rn und die
Auslenkung aus der Ruhelage ~un (t):
~rn (t) = ~rn + ~un (t).
(4.89)
Somit ergibt sich:
~ t) ∝
AB (B,
X
~
~
ei~rn ·K ei~un (t)·K e−iω0 t .
Für kleine Auslenkungen ~un (t) lässt sich die Exponentialfunktion entwickeln:
X
~
~ t) ∝
~ . . .]e−iω0 t .
AB (B,
ei~rn ·K [1 + i~un (t) · K
(4.90)
(4.91)
Setzen wir für die Auslenkungen ~un (t) ebene Wellen an:
1
~un (t) = ~u √ e±i~rn ·~q−ω(~q)t .
M
118
(4.92)
Durch Einsetzen erhalten wir neben den Termen der elastischen Streuung auch die der inelastischen:
X ~
~ · ~u √1 ei[ω0 ±ω(~q)]t .
~ t) ∝
ei(K∓q)·~rn iK
(4.93)
Ainel (B,
M
n
Es ergibt sich eine Streuwelle, deren Frequenz gerade um die Frequenz ω bezogen auf die
Primärwelle verschoben ist. Es ist klar, dass die Amplitude nur dann von Null verschieden
ist, wenn
ω = ω0 ± ω(~q)
~ ∓ ~q = ~k − ~k0 ∓ ~q = G
~
K
(4.94)
(4.95)
gilt. Multipliziert man beide Seiten mit ~ so ergibt sich
~ω − ~ω0 ± ~ω(~q) = 0
~ ∓ ~~q − ~G
~ = ~~k − ~~k0 ∓ ~~q − ~G
~ =0
~K
(4.96)
(4.97)
Diese beiden Gleichungen lassen sich als die Energie- und Impulserhaltung im klassischen
Sinne interpretieren. Wobei ~q der Quasiimpuls eines Teilchens — Phonons — ist.
4.4.1 Vergleich Neutronen- und Photonen-Spektroskopie
Der Zusammenhang zwischen Energie und Impuls bei Neutronen und bei Photonen:
Neutronen
En =
p2
,
2Mn
Mn = 1838, 65me = 1, 67 · 10−24 g.
(4.98)
Photonen
Eγ = pc,
c = 2, 99792 · 108 m/s.
119
(4.99)
6
10
4
10
2
10
0
10
-2
10
-4
10
-6
10
-8
10
-10
10
-12
10
-14
10
-16
10
-18
10
-20
10
0
1
2
3
4
5
6
7
8
9
10
10 10 10 10 10 10 10 10 10 10 10
Der wesentliche Unterschied zwischen den beiden Analysemethoden besteht in der Tatsache,
dass bei Vergleichbaren Energien die Neutronen deutlich mehr Impuls transportieren und
somit auch Anregungen am Rand der Brillouin-Zone ermöglichen. Photonen können hier nur
über so genannte virtuelle Zustände wechselwirken.
4.4.2 Die Raman-Spektroskopie
Betrachtet man sich die Frequenzen des sichtbaren Lichts, das bei der Raman-Spektroskopie
verwendet wird:
4π
−1
2k0 =
≈ 2 · 10−3 Å
(4.100)
λ
so wird klar, dass diese nur etwa 1/1000 des reziproken Gittervektors darstellt, d.h. es werden
nur Phononen tief im Inneren der Brillouin-Zone angeregt.
Eine einfallende Welle E0 erzeugt über den Suszeptibilitätstensor χ̂ eine Polarisation P~ in
Materie:
~0
P~ = ε0 χ̂E
(4.101)
Diese sich zeitlich ändernde Polarisation führt zur Abstrahlung einer Welle. Nach der Elektrodynamik ergibt sich pro Festkörpervolumen in Richtung ~s abgestrahlte Energiestromdichte
~ im Abstand r:
(Pointing-Vektor) S
2
4 2
~ = ω P sin (θ) ~s.
S(t)
16π 2 ε0 r2 c3
(4.102)
Dabei bezeichnet θ den von der Beobachtungsrichtung und der Schwingungsrichtung P~ eingeschlossene Winkel. Durch die bei Phononen entstehende Auslenkung der Atome bezüglich
120
ihrer Ruheposition beeinflusst die Suszeptibilität. Die Änderung der Suszeptibilität bei einer
Auslenkung der Atome aus ihrer Ruheposition lässt sich entwickeln:
∂ χ̂
χ̂ = χ̂0 +
u
(4.103)
∂u
Da nur Wellenzahlen q in der Nähe von Null betrachtet werden lässt sich vereinfacht schreiben
u = u0 cos(ω(~q)t) und für das elektrische Feld der einfallenden Welle E0 = E00 cos(ω0 t).
Somit ergibt sich für die Polarisation, wenn man beides in Gl.(4.101) einsetzt:
P~
= ε0 χ̂0 E00 cos(ω0 t) + ε0
∂ χ̂
u0 cos(ω(~q)t)E00 cos(ω0 t)
∂u
= ε0 χ̂0 E00 cos(ω0 t) +
∂ χ̂
+ε0 u0 E00 {cos([ω0 + ω(~q)]t) + cos([ω0 − ω(~q)]t)}
∂u
(4.104)
Das abgestrahlte Licht enthält neben dem elastischen Anteil mit der Frequenz ω0 (durch
Rayleigh-Streuung) die so genannten Raman-Seitenbanden mit ω0 ± ω(~q). Dabei wurde beim
Zustandekommen der Linie ω0 −ω(~q) ein Phonon erzeugt (Stokes-Linie) und bei der ω0 +ω(~q)
ein Phonon vernichtet (Anti-Stokes-Linie).
Schematische Darstellung der Verhältnisse
Experimenteller Aufbau zu Raman-Spektroskopie
121
4.4.3 Die Neutronen-Spektroskopie
Bei der Neutronen-Spektroskopie werden thermische Neutronen aus einem Kernreaktor nach
dem Durchlaufen durch eine Monochromator zur Streuung auf die probe geleitet. Es werden
thermische Neutronen verwendet, da diese ein günstiger Impuls/Energie-Verhältnis besitzen,
welches zu dem der Phononen passt. Somit kann die gesamte Brillouin-Zone abgetastet
werden. Es werden so genannte Dreiachsenspektrometer verwendet. Die Achsen sind:
1. Um eine bestimmte Energie des einfallenden Strahls zu selektieren, muss die die Probe
mit Analysator und Detektor um eine Achse im Zentrum des Monochromator gedreht
werden.
2. Um die Probe unter verschiedenen Winkel zu treffen, muss der Analysator und der
Detektor auch noch um die Achse durch die Probe gedreht werden können.
3. Um schließlich eine bestimmte Energie zu detektieren, muss der Detektor um die Achse
durch den Analysator gedreht werden können.
Die verwendeten Komponenten sind:
Neutronenquelle Es kommt entweder einen Hochflussreaktor, ein Beschleuniger oder eine
Spallationsquelle (Kernzertrümmerung, gepulst) zum Einsatz.
Monochromator/Analysator Hier wird ein bekannter Einkristall verwendet bei dem die
Bragg-Reflexion ausgenutzt wird, um eine Energie auszuwählen (großer Verlust an
Fluss).
Detektor Es wird ein Szintillator mit Photomultiplier eingesetzt.
122
Schematischer Aufbau eines Dreiachsenspektrometers
Detektor
Probe
Kernreaktor
Analysator
Monochromator
Darstellung eines Dreiachsenspektrometers
123
4.5 Effekte anharmonischer Gitterwechselwirkung
Konsequenzen harmonischer Wechselwirkung in Kristallen:
• Zwei Phononen beeinflussen sich nicht gegenseitig. Sie laufen ungestört durch einander
hindurch.
• Es gibt keine Wärmeausdehnung.
• Adiabatische und isotherme elastische Konstanten sind gleich.
• Die elastische Konstanten sind von Druck und Temperatur unabhängig.
• Die Wärmekapazität wird bei hohen Temperaturen (T > θ) konstant.
4.5.1 Die Wärmeausdehnung
wir hatten die Wechselwirkung zwischen den Atomen eines Gitters als harmonisch genähert.
Damit lässt sich die Wärmeausdehnung nicht verstehen. So nehmen wir auch noch höhere
Terme für die Wechselwirkungsenergie mit hinzu. Die Wechselwirkungsenergie hänge folgendermaßen vom Abstand x der Atome bei 0K ab:
U = cx2 − gx3 − f x4
(4.105)
Dabei sind c, g und f positive Konstanten. Der x3 -Term gibt die Asymmetrie des Potentials
wieder.
Der Mittelwert des Abstandes zweier Atome in diesem Potential lässt sich mit Hilfe des
Boltzmann-Faktors berechnen:
R +∞ − U (x)
xe kB T dx
(4.106)
hxi = R−∞
U (x)
+∞ − k T
B
dx
−∞ e
Bei kleinen Auslenkungen lassen sich die Integranden wieder nähern:
Z +∞
Z +∞
2
U (x)
f x5
gx4
−k T
− kcx T
+
dx
xe B dx ≈
e B
x+
kB T
kB T
−∞
−∞
4
gx3
gx3
f x4
+ fx
mit e kB T kB T ≈ 1 +
+
+ ···
kB T
kB T
√
3 π g p
√
=
(kB T )3 ,
4
c5
r
Z +∞ U (x)
Z +∞
2
πkB T
−k T
− kcx T
.
e B dx ≈
e B =
c
−∞
−∞
(4.107)
Und hieraus ergibt sich für die Wärmeausdehnung im klassischen Bereich:
hxi =
3g
kB T.
4c2
124
(4.108)
Gitterkonstante von festem Argon über der Temperatur
Der lineare Wärmeausdehnungskoeffizient ist dann schließlich wie folgt definiert:
α=
1 dl
l dT
(4.109)
Bei isotropen Medien ist der Volumenausdehnungskoeffizient gerade das Dreifache des linearen Ausdehnungskoeffizienten:
1 dV
αV = 3α =
(4.110)
V dT
Es lässt sich zeigen (Genaueres in Ashcroft/Mermin oder Ibach/Lüth), dass der Ausdehnungskoeffizient bei niedrigen wie auch bei hohen Temperaturen die gleiche Temperaturabhängigkeit — T 3 bzw. konstant — wie die spezifische Wärme hat.
4.5.2 Die Wärmeleitung
Phononen können nur an:
• an Kristallfehlern,
• an den Oberflächen des Kristalls
• oder an anderen Phononen
streuen.
Bei einer harmonischen Gitterwechselwirkung wäre die Wechselwirkung unter den Phononen nicht möglich. Die mittlere freie Weglänge l ist der Weg den die Phononen im Mittel
125
zwischen zwei Streuprozessen zurücklegen. Die mittlere freie Weglänge l nimmt mit steigender Temperatur ab. Dies lässt sich damit erklären, dass bei höheren Temperaturen mehr
Phononen angeregt sind und somit die Streuwahrscheinlichkeit erhöht ist. Fall hoher Temperaturen gilt l ∝ 1/T , da hier die Anzahl der angeregten Zustände proportional zur Temperatur
ist.
So folgt aus einem klassischen Ansatz für die Wärmeleitzahl, den Anteil des Phononensystems:
1
W
J
λ = cvs ρl
=
,
(4.111)
3
smK
mK
wobei c die Wärmekapazität, vs die Schallgeschwindigkeit, ρ die Dichte des Materials und l
die mittlere freie Weglänge. Da bei niedrigen Temperaturen die Zunahme der Wärmekapazität
und bei hohen Temperaturen die Abnahme der mittleren freien Weglänge das Verhalten
dominiert ergibt sich folgendes Bild:
Wärmeleitzahl von hochreinem NaCl über der
Temperatur
Soll nun Wärme durch das Phononensystem von einer Seite eines Kristalls auf die andere
transportiert werden sind eine wesentliche Voraussetzungen zu erfüllen:
Die Phononen müssen lokal thermalisieren, da es sonst nicht möglich ist zwei unterschiedliche Temperaturen an den unterschiedlichen Enden des Kristalls zu definieren.
Dieses Thermalisieren kann allerdings nicht durch Stoßprozesse mit Kristallfehlern oder
mit der Kristalloberfläche erfolgen, da hierbei keine Energie umverteilt wird. Das gestreute
Phonon hat vor und nach dem Streuprozess noch die selbe Energie.
126
Allerdings auch Drei-Phononenprozesse
~1 + K
~2 = K
~3
K
(4.112)
führen nicht zu einer Thermalisierung. Der Gesamtimpuls des Phononensystems ändert sich
hierbei nicht.
Eine Störung des thermischen Gleichgewichts bewegt sich mit konstanter
Driftgeschwindigkeit durch den Kristall ohne zu thermalisieren.
Der Gesamtimpuls
J~ =
X
~
nK
~ ~K
(4.113)
~
K
~ 3 −K
~ 1 −K
~ 2 = 0 erhalten. n ~ ist die Anzahl der Phononen mit dem Wellenvektor
bleibt hier K
K
~
K.
Auf diese Art würde sich nur eine Phononenquelle auf der einen Seite und
eine Phononensenke auf der anderen Seite ergeben, wenn auf der einen
Seite Phononen durch Strahlungabsorption erzeugt und auf der anderen
Seite durch Strahlungsemission wieder vernichtet werden.
Problem!
4.5.3 Umklapp-Prozesse
Rufen wir ins Gedächtnis, dass auch ein Impuls an das Gitter übertragen werden kann. Somit
lässt sich der für die Wärmeleitung relevante Prozess durch
~1 + K
~2 = K
~3 + G
~
K
(4.114)
~ wieder den reziproken Gittervektor dar. Diese Prozesse wurden
beschreiben. Dabei stellt G
von Peierls entdeckt und werden Umklapp-Prozesse genannt.
127
Ky
Ky
K1
K1
K2
K2
K3
Kx
Kx
K3
K1+K2
G
Umklapp-Prozess
Normal-Prozess
Beim Umklapp-Prozess reicht der Wellenvektor des erzeugten Phonons aus der ersten Brillouin.Zone heraus. Die beiden beteiligten Phononen müssen einen ausreichend große Wellenvektor aufweisen.
4.5.4 Abschließende Bemerkungen zu Phononen
Regt man Phononen auf einer Seite des Kristalls an und beobachtet in welcher räumlichen
Verteilung die Phononen auf der gegenüberliegenden Seite des Kristalls ankommt, so kann
man auf de interne Struktur des Kristalls zurück schließen, d.h. auf den Kristallaufbau schließen und sogar defekte abbilden. Einige Beispiele für die räumlichen Verteilungen:
128
Verteilung bei Quarz
Verteilung bei Silizium bei einer [111]-Fläche
129
Verteilung bei Gallium-Arsenid
TA-Mode1
TA-Mode2
130
Verteilung bei Gallium-Arsenid
131
5 Elektronen in Festkörpern
5.1 Das freie Elektronengas
Bei dieser Vorstellung werden Elektronen als frei verschiebbar zwischen den Atomrümpfen
angesehen, als eine Art von Gas mit einer entsprechenden Energieverteilung (Boltzmann),
das den Zwischengitterraum isotrop auffüllt.
5.1.1 Das Drude-Modell(1900)
Rumpfelektronen
Kern
Atom
Valenzelektronen
Festkörper
Die Dichte der Elektronen lässt sich leicht abschätzen:
n=
N
ρm
=Z
L.
V
A
(5.1)
Dabei bezeichnet Z die Zahl der Valenzelektronen, ρm die Massendichte, A das Atomgewicht
und L die Loschmidtzahl/Avogadro-Konstante (=6, 02214 · 1023 mol−1 ). Damit ergibt sich
z.B. für n einen Bereich von 1022 cm−3 (Cäsium) bis 2 · 1023 cm−3 (Beryllium).
Mit diesem Modell lässt sich recht einfach die elektrische und thermische Leitfähigkeit
abschätzen.
132
5.1.1.1 Die elektrische Leitfähigkeit im Drude-Modell
~ = |e|n~v
~j = σ E
(5.2)
~ das elektrische Feld, e die
~j bezeichnet die Stromdichte, σ die elektrische Leitfähigkeit, E
Elementarladung, n die Ladungsträgerkonzentration und ~v die Geschwindigkeit der Ladungsträger.
Die Geschwindigkeit, welche die Elektronen erreichen im Mittel erreichen, lässt sich durch
eine Zeit abschätzen, die den Elektronen gegeben wird um im elektrischen Feld beschleunigt
zu werden.
~
eEτ
m
Somit ergibt sich für die Stromdichte mit Gl.(5.2):
2 ~
~j = ne τ E
m
~vm = −
(5.3)
(5.4)
und so ergibt sich für die Leitfähigkeit σ
σ=
ne2 τ
m
(5.5)
Die Beziehung für die elektrische Leitfähigkeit lässt sich umkehren, um aus der Bestimmung
der Leitfähigkeit auf die Relaxationszeit zurück zu schließen:
τ=
mσ
ne2
(5.6)
Typische Werte für die Relaxationszeit bei Raumtemperatur liegen in einem Bereich zwischen
10−14 s bis 10−15 s.
5.1.1.2 Hall-Effekt und Magnetwiderstand
--------------
Ex
Ey
H++++++++++++++
jx
Wenn sich Elektronen in einem Magnetfeld bewegen erfahren sie die Lorentz-Kraft:
e
~
FL = − ~v × H
c
(5.7)
Im Wesentlichen sind zwei Größen von Interesse, um den Hall-Effekt zu charakterisieren:
133
Der Magnetwiderstand
Ex
jx
(5.8)
Ey
jx H
(5.9)
ρ(H) =
Der Hall-Koeffizient
RH =
Um diese Größen im Drude-Modell ausdrücken zu können, betrachten wir zunächst die auftretenden Stromdichten ~jx und ~jy . Die auf jedes Elektron wirkende ortsunabhängige Kraft
f~ lässt sich wie folgt ausdrücken:
~
~ + ~v × H )
f~ = −e(E
c
(5.10)
Damit ergibt sich für den Impuls des Elektrons:
d~
p
~ + p~ × H)
~ − p~
= −e(E
dt
mc
τ
(5.11)
Hierbei stellt der Ausdruck in der Klammer den Impulszuwachs durch die externen Felder
und der rechte Term die Relaxation auf den Gleichgewichtswert dar. Im Stationären zustand
muss für die einzelnen Komponenten gelten:
px
τ
py
0 = −eEy + ωc px −
τ
0 = −eEx − ωc py −
wobei ωc =
eH
mc
(5.12)
ist. Multiplizieren wir diese Gleichungen mit − neτ
m so folgt:
σ0 Ex = ωc τ jy + jx
(5.13)
σ0 Ey = −ωc τ jx + jy
(5.14)
dabei bezeichnet σ0 die Gleichstromleitfähigkeit des Drude-Modells ohne Magnetfeld. Das
Hall-Feld ist dadurch bestimmt, dass der transversale Strom jy verschwindet. Durch Null
setzen der Stromdichte jy = 0 und einsetzten ind Gl.(5.14) erhalten wir:
Ey = −
ωc τ
eHτ m
H
jx = −
jx = −
jx
2
σ0
mcne τ
nec
(5.15)
und somit ergibt sich für den Hall-Koeffizienten:
RH = −
1
nec
(5.16)
Dies ist ein erstaunliches Ergebnis, da es bedeutet, dass keinerlei materialspezifischen Parameter eingehen außer der Ladungsträgerkonzentration.
134
5.1.1.3 Die thermische Leitfähigkeit im Drude-Modell
Ein eindrucksvoller Erfolg des Drude-Modells zu seiner Zeit bestand in der Tatsache, dass es
in der Lage war das Wiedemann-Franz-Gesetz (1853) zu erklären. Das Wiedemann-FranzGesetz besagt, dass der Quotient σκ aus thermischer und elektrischer Leitfähigkeit direkt
proportional zur Temperatur ist.
Das Drude-Modell erklärt dieses Phänomen unter der Annahme, dass die Elektronen
hauptsächlich für die Wärmeleitung in Metallen verantwortlich sind. Der Wärmestrom lässt
sich wie folgt darstellen:
~j q = −κ∇T
(5.17)
Zur Herleitung betrachten wir die Situation in der ein eindimensionale Wärmeleiter an einer
Seite geheizt und auf der anderen gekühlt wird. Dadurch stellt sich ein Temperaturgradient
entlang der Raumrichtung ein. Zunächst betrachten wir die pro Elektron getragene thermische Energie ε(T ). Die Elektronen nehmen ihre thermische Energie durch Stöße auf. Fand
der letzte Stoß bei Position x0 statt so besitzt das Elektron die thermische Energie ε(T [x0 ]).
Elektronen die von der heißeren Seite her kommen, hatten im Mittel ihren letzten Stoß am
Ort x−vτ und tragen deshalb die thermische Energie ε(T [x−vτ ]). Der Anteil der Elektronen
an der Wärmeleitung ergibt sich somit als Produkt ihrer Anzahl pro Einheitsvolumen, ihrer
Geschwindigkeit und der Energie pro Elektron n2 vε(T [x − vτ ]). Analoges lässt sich über die
Elektronen von der kalten Seite sagen, somit ergibt sich hier n2 (−v)ε(T [x+vτ ]). der gesamte
Wärmestrom setzt sich aus diesen beiden Anteilen zusammen:
1
j q = nv[ε(T [x − vτ ]) − ε(T [x + vτ ])].
(5.18)
2
Unter der Annahme, dass sich die Temperatur entlang von l = vτ kaum ändert lässt sich
um x entwickeln:
dT
dT
T (x − vτ ) = T −
vτ = T − l
dx
dx
dε
dT
ε(T + ∆T ) = ε(T ) +
∆T mit ∆T = − vτ
dT
dx
dT
dε
−
.
j q = nv 2 τ
(5.19)
dT
dx
Durch den Übergang in drei Dimensionen mit jeweils gleichen Geschwindigkeitskomponenten
dE/dT
N dε
(hvx2 i = hvy2 i = hvz2 i = 13 v 2 ) und ndε
= cv der spezifischen WärmekapadT = V dT =
V
zität der Elektronen, ergibt sich:
~j q = 1 v 2 τ cv (−∇T )
3
(5.20)
und somit
1
1
κ = v 2 τ cv = vlcv
(5.21)
3
3
hierbei ist v 2 das mittlere Geschwindigkeitsquadrat der Elektronen. Dividieren wir nun dieses
Ergebnis durch die zuvor bestimmte Leitfähigkeit so erhalten wir:
1
cv mv 2
κ
= 3 2
σ
ne
135
(5.22)
Drude schätzte die spezifische Wärmekapazität des Elektronengases mit der eines klassischen
realen Gases ab cv = 32 nkB und die kinetische Energie 12 mv 2 = 32 kB T . Daraus resultiert:
κ
=
σ
13
3 2 nkB 3kB T
ne2
3
=
2
kB
e
2
T.
(5.23)
Somit ist das Verhältnis proportional zur Temperatur mit einer Proportionalitätskonstante
die nur allgemeinen Konstanten abhängt. Die Konstante
κ
3
=
σT
2
kB
e
2
= 1, 11 × 10−8 W Ω/K 2
(5.24)
wird als Lorenz-Zahl bezeichnet. Sie ist etwa halb so groß, wie der experimentell beobachtete
Wert.
Element
Li
Na
K
Rb
Cu
Ag
Au
Be
Mg
Nb
Fe
Zn
Cd
Al
In
Ti
Sn
Pb
Bi
Sb
κ [W/cmK]
0,71
1,38
1,0
0,6
3,85
4,18
3,1
2,3
1,5
0,52
0,8
1,13
1,0
2,38
0,88
0,5
0,64
0,38
0,09
0,18
273K
κ/σT [10−8 WΩ/K2 ]
2,22
2,12
2,23
2,42
2,20
2,31
2,32
2,36
2,14
2,90
2,61
2,28
2,49
2,14
2,58
2,75
2,48
2,64
3,53
2,57
κ [W/cmK]
0,73
3,82
4,17
3,1
1,7
1,5
0,54
0,73
1,1
1,0
2,30
0,80
0,45
0,60
0,35
0,08
0,17
373K
κ/σT [10−8 WΩ/K2 ]
2,43
2,29
2,38
2,36
2,42
2,25
2,78
2,88
2,30
2,19
2,60
2,75
2,54
2,53
3,35
2,69
5.1.2 Das freie Elektronengas im Potentialkasten
In diesem Abschnitt betrachten wir die Situation, in der eine “freies” Elektronengas in einem
Kasten eingeschlossen ist. In der folgenden Abbildung ist die Situation in einer Dimension
skizziert, wie sie in einem Kristall herrscht.
136
Energie
h
h
Evac
+ + + + + + + + + + + +
Ortskoordinate x
Da die Austrittsarbeiten (5eV entspricht ca. 50000K) sehr hoch sind, kann man das Potential
durch einen Kasten mit ebenen Boden und unendlich hohen Wänden annähern. Damit lässt
sich die stationäre Schrödinger-Gleichungen in Einelektronennäherung wie folgt schreiben:
−
~2
4ψ(~r) + V (~r)ψ(~r) = E 0 ψ(~r)
2m
wobei das Kastenpotential die Form
(
V0 = const.
V (x, y, z) =
∞
sonst
für
0 ≤ x, y, z ≤ L
(5.25)
(5.26)
besitzt. Mit E = E 0 − V0 gilt:
−
~2
4ψ(~r) = Eψ(~r).
2m
(5.27)
Durch die Randbedingungen ergibt sich folgende Forderungen für die Wellenfunktion:
ψ = 0 für x = 0 und x = L y,z beliebig sowie zwischen 0 und L
y = 0 und y = L x,z beliebig sowie zwischen 0 und L
z = 0 und z = L x,y beliebig sowie zwischen 0 und L
Da die Wahrscheinlichkeit Eins ist das Elektron im Kasten anzutreffen, gilt für die Normierung von ψ(~r):
Z
ψ ∗ (~r)ψ(~r)d~r = 1.
(5.28)
Kasten
Es ergeben sich folgende Lösungen der Schrödinger-Gleichung:
3/2
2
ψ(~r) =
sin(kx x) sin(ky y) sin(kz z).
L
137
(5.29)
Setzt man die Lösungen in die Schrödinger-Gleichung Gl.(5.27) ein, so ergeben sich folgende
Energiezustände:
~2 k 2
~2 2
E=
=
(k + ky2 + kz2 )
(5.30)
2m
2m x
Somit sind die Energiewerte die eines freien Elektrons, wobei wegen der Randbedingungen
Einschränkungen für die k-Werte bestehen, die natürlich für ein tatsächlich freies Elektron
nicht gegeben sind:
kx =
ky =
kz =
π
nx ,
L
π
ny ,
L
π
nz ,
L
(5.31)
mit
nx , ny , nz = 1, 2, 3 . . .
Im Dreidimensionalen stellen Flächen konstanter Energie E = ~2 k 2 /2m Kugeln im k-Raum
dar (vergl. Herleitung der Zustandsdichte bei Phononen). Damit sind auch hier wieder — wie
bei den Phononen — die möglichen Zustande diskrete Punkte im k-Raum. Jeder Zustand
nimmt ein Volumen von Vk = (π/L)3 ein.
Zur Berechnung der Zustandsdichte betrachten wir das Volumen, das zwischen den beiden
Kugelflächen E(~k) und E(~k) + dE eingeschlossen ist. Es wird nur ein Achtel der gesamten
Kugel im k-Raum betrachtet, da nx , ny und nz nur positive Werte annehmen können. Es
muss also das eingeschlossene Volumen durch das Volumen dividiert werden, das ein Zustand
einnimmt, um auf die Anzahl der Zustände zwischen den beiden Kugelschalen zu schließen.
ky
p/L
E(k)+dE
E(k)
kx
138
Es ergibt sich:
0
dZ =
1
4πk 2
8
| {z }
dk
|{z}
Oberfläche einer achtel Kugel
Wegen dE =
~2 k
m dk,
Schalendicke
3
L
π
| {z }
(5.32)
Volumen pro Zustand
folgt für die Anzahl der Zustände pro Kristallvolumen L3 :
dZ =
(2m)3/2 1/2
E dE
4π 2 ~3
(5.33)
Berücksichtigt man, dass ein Elektron einen Spin besitzt, ergibt sich für jeden Zustand eine
Doppelbesetzung mit Elektronen unterschiedlichen Spins:
D(E) =
(2m)3/2 1/2
E .
2π 2 ~3
(5.34)
D(E) wird üblicherweise in Einheiten von cm−3 eV−1 angegeben.
5.1.3 Das Fermi-Gas bei 0K
Wird die Temperatur auf 0K abgesenkt, so befinden sich Elektronen im Gegensatz zu Bosonen
nicht alle im Grundzustand, sonder müssen jeweils verschiedene Zustände einnehmen. Dies
hat zur Folge, dass Elektronen Zustände bis zu einem bestimmten Energie Niveau besetzen,
139
welches als Fermi-Energie EF0 bezeichnet wird. An jeder Stelle des Festkörpers gilt für die
Elektronendichte n:
Z
n=
∞
D(E)f (E, T )dE,
(5.35)
0
es geht also das Produkt aus der Zustandsdichte D(E) und der Besetzungswahrscheinlichkeit
in das Integral ein.
2 2
~ k
Im Modell des freien Elektronengases im Kasten stellt sich die Energie EF0 (~kF ) = 2mF
als Kugel im k-Raum dar mit einem Radius kF , welcher als Fermi-Radius bezeichnet wird.
Bei einer Temperatur von 0K ist die Besetzungswahrscheinlichkeit für E ≤ EF0 gleich Eins
und für E > EF0 gleich Null.
f(E)
1
0
0
EF
D(E)f(E)
E
E
140
0
EF
kz
ky
kx
E(k)=E0F
Somit ergeben sich einfache Zusammenhänge zwischen der Ladungsträgerdichte n und dem
Fermi-Radius kF bzw. der Fermi-Energie EF0 :
L3 kF3
→
3π 2
~2 √
3
9π 4 n2
2m
nL3 =
EF0
=
n=
kF3
3π 2
(5.36)
(5.37)
Eine weitere Konsequenz, dass es sich bei Elektronen um Fermiionen handelt und sie somit
bei T = 0 nicht in einem Grundzustand liegen, besteht in einer nicht verschwindenden inneren
Energie. Die innere Energie ist der Mittelwert über alle Zustände:
0
EF
Z
U=
0
3
D(E)EdE = nEF0 .
5
(5.38)
Es lassen sich sofort noch weitere Größen, wie die Fermi-Geschwindigkeit vF , die FermiTemperatur TF und der charakteristische Radius rs (dies ist der Radius einer Kugel mit dem
Volumen, das ein freies Elektron einnimmt), definieren:
vF
TF
~kF
m
EF0
=
k
sB
=
rs =
3
3
4πa30 n
a0 ist hier der Bohrsche Radius (~2 /me2 = 0,529 ×10−10 m).
Einige Werte für verschiedene Metalle
141
(5.39)
(5.40)
(5.41)
Metall
n
(1022 cm−3 )
Li
Na
Cs
Al
Cu
Ag
Au
4,62
2,53
0,86
18,07
8,47
5,87
5,9
rs
(a0 )
3,27
3,99
5,71
2,07
2,67
3,02
3,01
kF
(106 m−1 )
1,11
0,91
0,63
1,75
1,36
1,20
1,20
vF
(106 m/s)
1,29
1,05
0,74
2,03
1,57
1,39
1,39
EF0
(eV)
4,70
3,14
1,53
11,65
7,03
5,50
5,52
TF
104 K
5,45
3,64
1,78
13,52
8,16
6,38
6,41
5.1.4 Die Temperaturabhängigkeit der Fermi-Dirac-Verteilung
Betrachtet man ein Fermi-Gas bei einer endlichen Temperatur und fragt nach der Besetzungswahrscheinlichkeit f (E, T ) der Zustände im Gleichgewicht, ist dies eine typische Fragestellung der Thermodynamik. Wir betrachten die große Anzahl an Energieniveaus Ei , die im
Festkörper dicht liegen, mit dem Entartungsgrad gi und der Besetzungszahl ni (mit ni ≤ gi
wegen des Pauli-Prinzips). Im Gleichgewicht soll die freie Energie F stationär sein gegenüber
einer Variation der Besetzungszahlen, d.h:
δF =
X ∂F
δni = 0
∂ni
(5.42)
i
Die Erhaltung der Teilchenzahl lässt sich wie folgt ausdrücken:
X
δni = 0.
(5.43)
i
Findet ein Austausch zwischen zwei Niveaus k und l statt, muss wegen der Teilchenerhaltung
gelten:
∂F
∂F
δnk +
δnl = 0
(5.44)
∂nk
∂nl
und
δnk + δnl = 0.
(5.45)
∂F
∂F
+
= 0.
∂nk
∂nl
(5.46)
Daraus folgt:
Wir hatten keine speziellen Forderungen an die Niveaus gestellt und somit gilt dies für alle
∂F
Niveaus und man kann eine Konstante µ = ∂n
einführen, welche das chemische Potential
i
genannt wird. Für die freie Energie gilt:
F = U − TS
(5.47)
X
(5.48)
wobei U die innere Energie:
U=
i
142
ni Ei
und S die Entropie ist:
S = kB ln P
(5.49)
dabei wiederum ist P die Anzahl der möglichen Zustände. Die Anzahl der Möglichkeiten
Pi ein Elektron im Zustand Ei unterzubringen ist gi , für das zweite Elektron gi − 1 usw.
Insgesamt also:
Pi = gi (gi − 1)(gi − 2) . . . (gi − ni + 1) =
gi !
(gi − ni )!
(5.50)
Da die Elektronen ununterscheidbar sind, reduziert sich die Anzahl nochmals um den Faktor
ni ! und es ergibt sich dann insgesamt:
Pi =
gi !
ni !(gi − ni )!
(5.51)
Um alle Energien Ei zu berücksichtigen, muss das Produkt über alle möglichen Zustände
jeder Energie Ei gebildet werden:
P =
Y
Y
Pi =
i
i
gi !
ni !(gi − ni )!
und damit ergibt sich für die Entropie:
X
S = kB
[ln(gi !) − ln(ni !) − ln({gi − ni }!)]
(5.52)
(5.53)
i
Nun lassen sich die Fakultäten ln(n!) für große n nach der Stirlingschen Näherungsformel
nähern:
ln(n!) ≈ n ln(n) − n.
(5.54)
Dadurch lässt sich die Ableitung der freien Energie nach der Teilchenzahl ni in einem beliebigen Zustand i berechnen, welche dem chemischen Potential entspricht:
∂F
ni
µ=
= Ei + kB T ln
.
(5.55)
∂ni
gi − n i
Zur Berechnung der Besetzungszahlen lösen wir nach ni auf:
gi
ni =
e
Ei −µ
kB T
(5.56)
+1
Für die Wahrscheinlichkeit, dass ein quantenmechanischer Zustand besetzt ist, wobei auch
die entarteten Zustände als verschieden anzusehen sind, ergibt dann:
1
f (E, T ) =
exp
E−µ
kB T
(5.57)
+1
Diese Verteilung wird als Fermi-Dirac-Verteilung bezeichnet.
143
1,4
4
TF=EF/kB=5x10 K
1,2
f(E)
1,0
1K
300K
1000K
10000K
30000K
0,8
0,6
0,4
0,2
0,0
0
1
2
3
4
5
6
7
8
9
10
4
E/kB (x10 K)
5.1.5 Die spezifische Wärme der Elektronen
Nach dem klassischen Ansatz für ein freien Elektronengas würde man für die innere Energie
und damit für die spezifische Wärme erwarten:
UEl =
3nkB T
2
→
∂U
3nkB
=
∂T
2
(5.58)
Im Experiment beobachtet man einen völlig anderen Zusammenhang. Dies lässt sich darauf
zurück führen, dass es für Fermiionen wichtig ist bei einer Anregung auch einen unbesetzten
Platz vor zu finden. Somit können nur ein kleiner Teil der Elektronen um die Fermi-Energie
tatsächlich Energie aufnehmen.
144
3,0
4
TF=EF/kB=5x10 K
2,5
D(E)f(E)
2,0
T=
1K
T = 300K
T = 1000K
1,5
1,0
2kBT
0,5
0,0
0
1
2
3
4
5
6
7
8
9
10
4
E/kB (x10 K)
Die energetische Zone der beteiligten Elektronen liegt in einem Intervall der Breite 4kB T .
So kann nur der Bruchteil 4kB T /EF der freien Elektronen Energie aufnehmen. Schätzt man
die Energie pro Elektron mit kB T ab, so ergibt sich für die Größenordnung der inneren
Energie:
4k 2 T 2 n
U∼ B
(5.59)
EF
mit TF = EF /kB ergibt sich für die spezifische Wärme der Elektronen:
cV =
∂U
8kB nT
∼
∂T
TF
(5.60)
Es wird deutlich, dass wirklich nur ein kleiner Teil der Elektronen an der spezifischen
Wärmekapazität beteiligt sind, da TF ≈ 105 K ist.
Eine genauer Ableitung der spezifischen Wärme (siehe z.B. Ibach/Lüth) liefert:
cv ≈
π2
2
D(EF )kB
T
3
(5.61)
Da für die Ableitung keine Annahme für D(E) gemacht werden musste, lässt sich dieser
Zusammenhang dazu benutzen, um aus der experimentellen Bestimmung der spezifischen
Wärme auf die Zustandsdichte D(EF ) am Fermi-Niveau zu bestimmen.
145
Insgesamt setzt sich die spezifische Wärmekapazität in Festkörpern aus zwei Anteilen,
dem phononischen und dem elektronischen, zusammen. Bei kleinen Temperaturen ergibt
sich somit:
(5.62)
cv,ges = cv,el + cv,ph = γT + βT 3
|{z} |{z}
cv,el
cv,ph
Dies wird experimentell recht gut bestätigt:
Vergleicht man den experimentell bestimmten Koeffizienten des elektronischen Beitrags
γ zur spezifischen Wärme mit dem theoretischen, so fallen bei einigen Metallen deutliche
Abweichungen auf:
Metall
Li
Na
K
Cu
Ag
Al
Fe
Co
Ni
γexp (10−3 MolJ K2 )
1,7
1,7
2,0
0,69
0,66
1,35
4,98
4,98
7,02
γexp /γtheo
2,3
1,5
1,1
1,37
1,02
1,6
10,0
10,3
15,3
Eisen, Cobalt und Nickel sind Übergangsmetalle deren d-Orbitale nur teilweise gefüllt sind.
Diese d-Elektronen sind stärker an den Atomen lokalisiert, was zu einer geringerem Überlapp
der Wellenfunktion und somit zu schärferen Bändern führt. Damit haben sie einen großen
Betrag zur Zustandsdichte.
146
Werte für γ des Beitrags des freien Elektronen-Gases zur Wärmekapazität
I
II
III
IV
V
B
C
N
H
Li
1,63
0,749
Na
1,38
1,094
K
2,08
1,668
Be
0,17
0,500
Mg
1,3
0,992
Ca
Sc
2,9
10,7
1,511
Experimentelle γ in mJmol−1 K−2
Berechnete γ für freie Elektronen mJmol−1 K−2
Ti
3,35
V
9,26
Cr
1,40
Mn
9,20
Fe
4,98
Co
4,73
Ni
7,02
Al
Si
1,35
0,912
Cu
Zn
Ga
Ge
0,695 0,64 0,596
0,505 0,735 1,025
P
As
0,19
5.1.6 Elektrostatische Abschirmung in einem Fermi-Gas — Mott-Übergang
Wird in ein Metall eine zusätzliche Ladung eingebracht, so tritt eine Umlagerung der Elektronen auf, die das elektrische Feld dieser Ladung abschirmt. Nehmen wir an, dass durch die
zusätzliche Ladung ein Störpotential der Größe δU (mit |eδU | EF ) auftritt.
147
Die Änderung der Elektronenkonzentration δn lässt sich dann beschreiben:
δn(~r) = D(EF )|e|δU (~r).
(5.63)
Geht man davon aus, dass die Störungen δU (~r) durch die Verschiebung der Ladung δn(~r),
so sind diese beiden Größen durch die Poisson-Gleichung miteinander verknüpft:
∇2 (δU ) = −
δρ
e
e2
= δn = D(EF )δU.
ε0
ε0
ε0
(5.64)
Die Differentialgleichung hat eine Lösung in Kugelkoordinaten, wo
∇2 =
1 ∂ 2∂
r
r2 ∂r ∂r
(5.65)
e−λr
r
(5.66)
gilt, die lautet:
δU (r) = −α
mit λ2 = e2 D(EF )/ε0 . Für eine Punktladung ergibt sich α = e/(4πε0 ), da hier für λ → 0
der Abschirmeffekt verschwindet und sich das Potential einer Punktladung ergeben muss.
Die Länge rT F = 1/λ wird als Thomas-Fermi-Abschirmlänge bezeichnet:
r
rT F =
ε0
2
e D(E
148
F)
.
(5.67)
Eine derartig starke Abschirmung z.B. eines Coulomb-Potentials ist dafür verantwortlich,
dass in einem Metall die äußersten Valenzelektronen nicht mehr an die Atome lokalisiert
sind, da sie nicht mehr im Feld der Rumpfpotentiale gehalten werden können. Je geringer
die Elektronendichte desto größer die Abschirmlänge.
Man kann sich vorstellen, dass ab einer kritische Elektronenkonzentration nc Elektronen
keinen gebundenen Zustand mehr einnehmen können und somit metallisches Verhalten auftritt. Bei Konzentrationen unterhalb dieses Wertes sind noch Bindungen in der Potentialmulde möglich. Dieser Übergang wird als Mott-Übergang bezeichnet.
5.1.7 Glühemission bei Metallen
Wird ein Metall stark erhitzt beginnen Elektronen auszutreten. Dies widerspricht natürlich
der ursprünglichen Annahme, dass die Ränder des Potentialtopfs unendlich hoch sind. Die
Energiedifferenz EV ac − EF = Φ, die benötigt wird, um ein Elektron aus dem Metall freizusetzen, wird Austrittsarbeit genannt.
149
A
j
js
T2 > T1
j
T1
K
Ub
Gegen-
0
Zugspannung
U
Uh
Zur Berechnung der Temperaturabhängigkeit des Sättigungsstromes js von Elektronen,
die das Metall verlassen kann, setzt man ~j = en~v an. Nun berechnet man den Anteil der
Elektronen, die eine ausreichende Energie besitzen den Potentialwall zu überwinden. Strom
ergibt sich:
Z
e X
e
vx (~k)d~k
(5.68)
jx =
=
V
(2π)3 E>EF +Φ,vx (~k>0)
~k
Mit der Zustandsdichte im k-Raum V /(2π)3 . Die Summe ebenso wie das Integral erstreckt
sich nur über nach der Fermi-Dirac-Verteilung besetzte Zustände 5.57. Damit multipliziert,
vx = ~k/m gesetzt und die zweifache Spinentartung berücksichtigt, liefert dann:
Z inf
Z inf
2e~
dky dkz
jx =
dkx kx f (E(~k), T )
(5.69)
(2π)3 m − inf
kx,min
Da die Austrittsarbeit Φ groß gegenüber kB T ist lässt sich die Fermi-Dirac-Statistik durch
die Boltzmann-Statistik annähern:
Z inf
Z inf
Z inf
e~
2 2
2 2
2 2
dkx kx e−(~ kx /2mkB T −EF /kB T )
jx = 3
dky e−~ ky /2mkB T
dkz e−~ kz /2mkB T
4π m − inf
kx,min
− inf
(5.70)
Da die Integrale faktorisiert sind lassen sie sich auswerten. Mit der Bedingung, dass die
kinetische Energie in x-Richtung größer als EF + Φ sein muss ergibt sich:
Z inf
Z
2 2
dkx kx e−(~ kx /2mkB T −EF /kB T ) =
kx,min
(EF +Φ)2m/¯
−(~2 kx2 −EF /2mkB T )
= mk~B2 T e−Φ/kB T (5.71)Es ergibt sich schließlich die so genannte Richardson-Dushman-Formel für die Sättigungsstromdichte
inf 1 dk 2 e
x
2
js =
−Φ
me
2 kB T
(k
T
)
e
B
2~3 π 2
150
(5.72)
In dieser Gleichung wurde angenommen, dass Elektronen deren Energie größer als EF + Φ
ist, das Metall mit einer Wahrscheinlichkeit von Eins verlassen können. Dies ist natürlich
nicht korrekt, da aus der quantenmechanischen Betrachtung folgt, dass Elektronen mit einer
Energie exakt von EF + Φ vollständig reflektiert werden und erst Elektronen mit einer gewissen Überschussenergie das Metallq
mit hoher Wahrscheinlichkeit verlassen können. So ergibt
sich noch ein zusätzlicher Faktor
kB T
EF +Φ ,
der den Sättigungsstrom deutlich reduziert.
Wie die Abbildung zeigt, verändert das von außen angelegte elektrische Feld E den Potentialverlauf und erniedrigt die Potentialbarriere. Der Verlauf des Potentials entsteht durch
die Coulomb-Bildkraft eines Elektrons vor einer Metallfläche und den Potentialverlauf des
externen Felds. Damit muss die Austrittsarbeit um:
s
Φ0 = Φ −
e3
= Φ − ∆Φ
4πε0
korrigiert werden.
151
(5.73)
Austrittsarbeiten der Elemente für polykristalline Proben
I
II
III
IV
V
VI
VII
H
Li
2,9
Na
2,75
K
2,30
Rb
2,16
Cs
2,14
Fr
VIII
He
Be
4,98
Mg
3,66
Ca
2,87
Sr
2,59
Ba
2,7
Ra
Austrittsarbeit φ/eV
Sc
3,5
Y
3,1
La
3,5
Ac
Ti
4,33
Zr
4,05
Hf
3,9
V
4,3
Nb
4,3
Ta
4,25
Cr
4,5
Mo
4,6
W
4,55
Mn
4,1
Tc
Re
4,96
Fe
4,5
Ru
4,71
Os
4,83
Co
5,0
Rh
4,98
Ir
5,27
Ni
5,15
Pd
5,12
Pt
5,65
Cu
4,65
Ag
4,28
Au
5,1
Zn
4,33
Cd
4,22
Hg
4,49
B
4,45
Al
4,28
Ga
4,2
In
4,12
Tl
3,84
C
5,0
Si
4,85
Ge
5,0
Sn
4,42
Pb
4,25
N
O
F
Ne
P
S
Cl
Ar
As
3,75
Sb
4,55
Bi
4,22
Se
5,9
Te
4,95
Po
Br
Kr
I
Xe
At
Rn
5.1.8 Unzulänglichkeiten des freien Elektronen-Modells
5.1.8.1 Widersprüche bei den Transportkoeffizienten freier Elektronen
Hall-Koeffizient: Die Theorie des freien Elektronengases ergibt einen Hall-Koeffizienten
1
RH = nec
, der unabhängig von der Temperatur, Relaxationszeit oder der Stärke des
Magnetfeldes ist. Die Experimente zeigen ein anderes Verhalten. So hat der HallKoeffizient für Aluminium bei hohen Magnetfeldern sogar ein anderes Vorzeichen, als
das Modell vorhersagt.
Magnetwiderstand: Der Magnetwiderstand sollte nach dem Modell unabhängig von der
elektrischen Feldstärke sein. Die Experimente zeigen aber, dass der Widerstand von
Edelmetallen (wie z.B. Kupfer, Gold, Silber) mit dem elektrischen Feld unbeschränkt
zu wachsen scheint. Der Magnetwiderstand ist von der Präparation der Probe und
deren Orientierung im Magnetfeld abhängig.
Thermoelektrisches Feld: Das Vorzeichen der Koeffizienten für verschiedene Beiträge wird
nicht richtig wiedergegeben. Nur die Größenordnung der Beiträge stimmen.
Wiedemann-Franzsches Gesetz: Die Reproduktion ist bei hohen Temperaturen und bei
niedrigen Temperaturen gut, allerdings ist im Zwischenbereich der Quotient κ/σT
temperaturabhängig.
Temperaturabhängigkeit der Gleichstromleitfähigkeit: Die Temperaturabhängig der Gleichstromleitfähigkeit wird nicht wiedergegeben. Sie kann nur durch eine Temperaturabhängigkeit der Relaxationszeit τ in das Modell “künstlich” eingebaut werden.
Richtungsabhängigkeit der Gleichstromleitfähigkeit: In manchen Metallen hängt die Gleichstromleitfähigkeit von der relative Richtung des elektrischen Feldes ab. Der Strom muss
in diesen Metallen nicht entlang der Feldlinien fließen.
Wechselstromleitfähigkeit: Die Frequenzabhängigkeit ist deutlich komplexer, als es das
einfache Modell der freien Elektronen wiedergeben kann. So werden die optischen
152
Eigenschaften wie die Reflektivität schon bei Metallen wie Natrium nicht richtig beschrieben.
5.1.8.2 Widersprüche bei den statischen thermodynamischen Voraussagen
Linearer Term in der Wärmekapazität: Die Theorie erklärt den Faktor γ des linearen
Terms der Wärmekapazität sehr unzulänglich. Experimenteller und theoretischer Wert
unterscheidet sich für Übergangsmetalle um eine Größenordnung.
Kubischer Term in der Wärmekapazität: Es gibt kein Argument, welches durch das Modell des freien Elektronengases begründet ist, warum die Wärmekapazität bei tiefen
Temperaturen durch den elektronischen Beitrag bestimmt sein soll. Experimente zeigen aber, dass es bei Metallen eine deutliche Korrektur zum T 3 -Gesetz gibt.
Kompressibilität der Metalle: Die Theorie des freien Elektronengas liefert recht gute Werte für den Kompressionsmodul unterschiedlicher Metalle. Dennoch ist offensichtlich,
dass bei einer genaueren Elektron-Elektron-Wechselwirkung nicht der Einfluss der
Atomrümpfe vernachlässigt werden kann.
5.1.8.3 Grundsätzliche Fragen
Wodurch ist die Anzahl der Leitungselektronen bestimmt: Es wurde vereinfacht angenommen, dass alle Valenzelektronen zu Leitungselektronen werden und alle Rumpfelektronen am Atom verbleiben. Dies muss selbstverständlich nicht so sein.
Warum sind einige Elemente Nichtmetalle: Eine noch deutliche Diskrepanz wird durch
diese Frage deutlich. Es ist nicht zu verstehen, warum Bor ein Isolator ist, während
Aluminium, das der gleichen Hauptgruppe angehört und nur in der nächsten Periode
steht, einen guter Leiter darstellt.
5.1.8.4 Zusammenfassung der Annahmen des freien Elektronengases
1. Näherung der freien Elektronen: Die Atomrümpfe spielen eine untergeordnete Rolle.
Die Stöße haben keine Auswirkung auf die Bewegung der Elektronen. Die Atomrümpfe
gewährleisten nur die Ladungsneutralität.
2. Näherung unabhängiger Elektronen: Wechselwirkungen unter den Elektronen werden
vernachlässigt (verdünntes Gas).
3. Relaxationszeitnäherung: Es wird vorausgesetzt, dass die Elektronenkonfiguration zum
Zeitpunkt des Stoßes keine Einfluss auf das Stoßergebnis hat.
153
5.2 Energiebänder
5.2.1 Allgemeine Überlegungen
Berücksichtigt man das Potential, welches durch Atomrümpfe moduliert wird, so ergibt sich
für die stationäre Schrödinger-Gleichung:
~2 2
Hψ = −
∇ + V (~r) ψ(~r) = Eψ,
(5.74)
2m
wobei
V (~r) = V (~r + ~rn );
~rn = n1~a1 + n2~a2 + n3~a3 .
(5.75)
Auch hier beschreibt ~r einen beliebigen Translationsvektor im dreidimensionalen periodischen
Gitter.
Ein periodisches Potential lässt sich in eine Fourier-Reihe entwickeln:
X
~
V (~r) =
VG~ eiG·~r .
(5.76)
~
G
~ ein reziproker Gittervektor:
Auch hier ist G
~ = h~g1 + k~g2 + l~g3
G
mit
h, k, l
ganzzahlig.
Der Allgemeine Ansatz zur Lösung der Schrödinger-Gleichung hat die Form:
X
~
ψ(~r) =
C~k eik·~r .
(5.77)
(5.78)
~k
Dabei ist ~k ein reziproker Gitterpunkt, der mit den Randbedingungen in Einklang zu bringen
ist. In die Schrödinger-Gleichung eingesetzt ergibt sich:
X ~2 k 2
~k
2m
~
Ck~0 eik·~r +
X
~0
~
Ck~0 VG~ ei(k +G)·~r = E
~
k~0 G
X
~
C~k eik·~r .
(5.79)
~k
~
Durch Umbenennen der Summationsindizies folgt (k~0 = ~k − G):


2 2
X ~
X
~ k
eik·~r 
− E C~k +
C~k−G~ VG~  = 0.
2m
~k
(5.80)
~
G
Die Bedingung gilt für jeden Ort ~r, so muss der Ausdruck, der nicht von ~r abhängt, für jedes
~k verschwinden. Das bedeutet:
2 2
X
~ k
− E C~k +
C~k−G~ VG~ = 0.
(5.81)
2m
~
G
154
Dies ist ein Satz von Gleichungen, der die Schrödinger-Gleichung im Wellenzahlraum darstellt.
~ unterscheiden. Das gesamte
Es koppeln nur Entwicklungskoeffizienten, deren ~k sich um G
Problem zerfällt in N Probleme (N Zahl der Elementarzellen), dabei ist jedem ein Vektor
~k zugeordnet. Die N Gleichungen liefern jeweils eine Lösung deren ~k sich gerade um G
~
unterscheiden, die sich als Superposition von ebenen Wellen darstellen lassen. Somit ist es
möglich, die Energieeigenwerte E mit k zu indizieren. Zu E~k = E(~k) gehört jeweils die
folgende Wellenfunktion:
ψ~k (~r) =
X
~
~
C~k−G~ ei(k−G)·~r .
(5.82)
~
G
oder
ψ~k (~r) =
X
~
~
~
C~k−G~ eik·~r e−iG·~r = u~k (~r)eik·~r .
(5.83)
~
G
~ Bei periodischen Randbedinu~k (~r) ist eine Fourier-Reihe über den reziproke Gittervektor G.
~
gungen ergibt, dass der Wellenzahlvektor k folgende Werte annehmen kann:
kx = 0, ±2π/L, ±4π/L, . . . , ±2πnx /L
ky = 0, ±2π/L, ±4π/L, . . . , ±2πny /L
(5.84)
kz = 0, ±2π/L, ±4π/L, . . . , ±2πnz /L
L ist wieder die Ausdehnung des Kristalls. Nach den Quantenzahlen kx , ky , kz oder nach
nx , ny , nz lassen sich die Quantenzustände indizieren. Die Lösung
~
ψ~k (~r) = u~k (~r)eik·~r
(5.85)
stellt eine modulierte ebene Welle mit einem Modulationsfaktor der die Periode des Gitters
aufweist:
u~k (~r) = u~k (~r + r~n ).
(5.86)
Dies wird Blochsches Theorem und die durch Gl.(5.83) - Gl.(5.86) werden als Bloch-Wellen
oder als Bloch-Zustände eines Elektrons bezeichnet.
155
uk(x)
Re(ψ)
cos(kx+ϕ)
uk(x)cos(kx+ϕ)
x
Die Periodizität des Gitterpotentials hat Konsequenzen auf die Bloch-Zustände. Aus der
~ 00 =
allgemeinen Darstellung in Gl.(5.83) kann man durch Umbenennen der Gittervektoren G
0
~
~
G −G


X
X
~ 0 ·~
~00
~
~ r −iG
i(~k+G)·~
r
ψ~k+G~ (~r) =
C~k+G−
e
=
C~k−G~00 e−iG ·~r  eik·~r = ψ~k (~r). (5.87)
~0 e
~ G
~0
G
G~00
das bedeutet:
ψ~k+G~ (~r) = ψ~k (~r).
(5.88)
Bloch-Wellen die sich um einen reziproken Gittervektor unterscheiden sind gleich. Damit
folgt durch Anwendung der Schrödinger-Gleichung:
Hψ~k (~r) = E(~k)ψ~k (~r).
(5.89)
~ verschobenen Zustand:
und im Fall eines um G
~ ~ ~ (~r).
Hψ~k+G~ (~r) = E(~k + G)ψ
k+G
(5.90)
und damit nach Gl.(5.88) folgt:
~ ~ (~r).
Hψ~k (~r) = E(~k + G)ψ
k
(5.91)
und damit folgt wiederum aus Gl.(5.89) und Gl.(5.91):
~
E(~k) = E(~k + G).
156
(5.92)
Damit sind die Eigenwerte E(~k) im k-Raum periodisch. Analog zu der Dispersionsrelation
der Phononen die ja auch im Wellenzahlraum periodisch war. Die Elektronenzustände lassen
sich als Energieflächen E = E(~k) im reziproken Raum darstellen. Diese Energieflächen heißen
Bänderschema.
5.2.2 Näherung des quasi-freien Elektrons
Bei diesem Grenzfall denkt man sich das Potential beliebig klein allerdings schon mit der
Forderung nach der Periodizität. Dies führt zu der Dispersionsrelation der freien Elektronen
2 k2
E(k) = ~2m
, bei dem aber die Forderung nach Periodizität erfüllt sein muss. Das heißt, es
muss gelten:
2
~ = ~ |~k + G|
~ 2.
E(~k) = E(~k + G)
2m
2πh
a .
E
~ →G=
Im eindimensionalen Fall gilt G
(5.93)
-4π/a
-2π/a
0π/a
2π/a
4π/a
k
Da die Dispersionsrelation die Periodizität aufweist, ist es völlig ausreichend, die erste BrillouinZone zu betrachten, da sie schon die gesamte Information enthält.
157
E
Reduktion auf die erste Brillouin-Zone
-1π/a
0π/a
1π/a
k
An den Grenzen der Brillouin-Zone (±G/2 = ±π/a) liegt eine Entartung von Zuständen vor,
da sich hier jeweils zwei Parabeln schneiden. Die zugehörigen ebenen Wellen haben folgende
Form:
e
iGx
2
und
G
ei[ 2 −G]x = e−
iGx
2
(5.94)
Unter Vernachlässigung von Termen höhere Ordnung (Beiträge von Wellen mit Vielfachen der
~ betrachten wir Wellen an der Zonengrenze des reziproken
Vektoren des reziproken Gitters G)
Gitters:
x
eiGx/2 + e−iGx/2 ∼ cos π
x2 iGx/2
−iGx/2
.
∼
e
−e
∼ sin π
2
ψ+ ∼
ψ−
(5.95)
(5.96)
Dabei handelt es sich um stehende Wellen mit räumlich feststehenden Nulldurchgängen.
Diese kann als Überlagerung einer einlaufenden und einer Bragg-reflektierten, ebenen Welle
angesehen werden. Die jeweils zugehörigen Wahrscheinlichkeitsdichten lauten:
x
∗
%+ = ψ +
ψ+ ∼ cos2 π
x2 ∗
2
%− = ψ− ψ− ∼ sin π
2
158
(5.97)
(5.98)
Das Bild zeigt eine schematische Darstellung der Situation. In Abbildung (a) ist das Potential
dargestellt, wobei die Positionen der Atomrümpfe durch Punkte gezeichnet sind. In Teil (b)
und (c) sind jeweils die Wahrscheinlichkeitsdichte der Wellen gezeichnet, die der Situation
am Brillouin-Zonenrand entspricht. Es handelt sich jeweils um stehende Wellen mit einer
Wellenzahl k = ±π/a. Die Welle in (b) ist bezüglich des freien Elektrons abgesenkt, da sie
eine erhöhte Aufenthaltswahrscheinlichkeit bei den Atomrümpfen besitzt, was einer tieferen
Lage im Potential entspricht. Die Welle in (c) liegt energetisch höher als ein freies Elektron bei
mittlerem Potential, da sie ihr Maximum der Aufenthaltswahrscheinlichkeit gerade zwischen
den Atomrümpfen besitzt.
Aus der Darstellung der Schrödinger-Gleichung im k-Raum Gl.(5.81) folgt nach einer
~
Translation um den Gittervektor G:
X
~2 ~ ~ 2
E−
|k − G| C~k−G~ =
VG~ 0 C~k−G−
~ G
~0
2m
~0
G
~0 = G
~ 00 − G
~
mit G
=
X
VG~00 −G~ C~k−G~ 00
(5.99)
VG~00 −G~ C~k−G~ 00
2
~ 2
E − ~ |~k − G|
(5.100)
~ 00
G
P
→
~ 00
G
C~k−G~ =
2m
Um die Koeffizienten C~k−G~ zu berechnen, geht man von kleinen Störungen aus, so dass man
in erster Näherung Eigenwert der Energie E gleich der Energie des freien Elektrons ist. Bei
der Entwicklung von C~k−G~ gehen vor allem die größten Koeffizienten ein, also dann wenn
der Nenner des Bruchs nahezu verschwindet:
E=
~2 ~ 2
~2 ~ ~ 2
|k| '
|k − G|
2m
2m
159
→
~k 2 ' |~k − G|
~ 2
(5.101)
Diese Beziehung ist äquivalent mit der Bragg-Bedingung. Das bedeutet, dass sich die stärksten Abweichungen vom freien Elektron durch das periodische Gitter bei Erfüllung der BraggBedingung im Kristall auftritt. Neben dem Koeffizienten C~k−G~ ist auch der Koeffizient C~k
~ = 0 aus Gl.(5.100) sieht. Somit ergeben sich folgende Gleichungen
wichtig wie man für G
für die beiden Koeffizienten:
~2 2
E−
k C~k − VG~ C~k−G~ = 0
(5.102)
2m
~2 ~ ~ 2
E−
|k − G| C~k−G~ − V−G~ C~k = 0
(5.103)
2m
wobei V0 = 0 ist. Die Lösung für die beiden Energiewerte lassen sich aus folgender Determinante bestimmen:
2
~ 2
VG~
2m k − E
2
= 0,
(5.104)
~ ~
~ 2 − E V−G~
|
k
−
G|
2m
h2 ~
~ 2 die freie Energie der Elektronen ist. Es lassen sich die beiden
wobei E~0 ~ = 2m
|k − G|
k−G
Lösungen der Säkulargleichung wie folgt schreiben:
r
1 0
1 0
±
0
E = (E~k−G~ + E~k ±
(E
− E~0 )2 + |VG~ |2
(5.105)
k
2
4 ~k−G~
Das bedeutet, die Aufspaltung der Energie am Zonenrand, an dem die Anteile der beiden
Wellen mit C~k und C~k−G~ gleich sind, beträgt:
∆E = E+ − E− = 2|VG~ |
Dadurch ergibt sich eine Dispersionsrelation wie sie im Bild dargestellt ist.
160
(5.106)
Es resultiert ein Energiefenster, dem keine reelle Wellenzahl zuzuordnen ist. Hier wird die
Wellenzahl imaginär, was einer gedämpften Welle als Lösung entspricht.
Betrachtet man auch höhere Energien so ergibt sich ein Wechsel zwischen erlaubten und
verbotenen Bändern.
5.2.3 Näherung der stark gebundenen Elektronen
Elektronen die Zustände besetzen die eng an das Atom im freien Zustand gebunden sind,
werden durch das Zusammenfügen zu einem Kristall diese starke Bindung nicht aufgeben.
Derartige Elektronen beschreibt man am Besten in der Näherung der starken Bindung. Hierbei
geht man von Orbitalen der freien Atome aus und betrachtet die Zustände im Kristall als
161
eine Überlagerung der Zustände von Elektronen freier Atome. Man geht bei der Einelektronennäherung wie folgt vor:
1. Es wird von der Schrödinger-Gleichung des freien Atoms ausgegangen und angenommen, dass deren Lösung bekannt ist.
2. Der gesamte Kristall wird wird aus Einzelatomen aufgebaut angesehen. Der HamiltonOperator eines Elektrons (Einelektronennäherung) wird nun unter Berücksichtigung der
Atome, die als Störung des Potentials des freien Atoms angesetzt werden. Dies erreicht
man durch eine Summation der Potentiale aller Atome außer des betrachteten.
Potentielle Energie
Potentielle Energie
V
0
0
V
(n-2)a
(n-1)a
na
(n+1)a
(n+2)a
(n+3)a
(n-2)a
(n-1)a
na
(n+1)a
(n+2)a
(n+3)a
3. Nun werden eine Überlagerung von unterschiedlichen ebenen Wellen angesetzt und
deren Koeffizienten im Fourier-Raum bestimmt. Die Lösungen müssen natürlich wieder
Bloch-Wellen sein.
4. Als Lösung erhält man durch das Zusammenfügen der Atome zu einem Kristall aus
dem Energieniveau Ei ein Band, wobei die mittlere Energie gegenüber Ei abgesenkt
ist.
162
5.2.4 Anzahl der Quantenzustände im Band
Wir betrachten einen Kristall der aus N Elementarzellen aufgebaut ist. Jede primitive Elementarzellen trägt einen unabhängigen Wert von k zu jedem Energieband bei — insgesamt
also N . Durch die beide unabhängigen Einstellungen des Elektronenspins ergeben sich so 2N
unabhängige Niveaus in jedem Band. Befindet sich in jeder Elementarzelle ein einwertiges
Atom so ist das Band zur Hälfte besetzt. Befindet sich in jeder Elementarzelle ein Atom mit
zwei Valenzelektronen oder besteht jede Elementarzelle aus zwei einwertigen Atomen so ist
das Band vollständig gefüllt.
163
Isolator
Metall
Halbmetall
E
E
E
EF
Eg
EF
p k
a
p k
a
E
E
p k
a
E
EF
Eg
EF
N(E)
N(E)
164
N(E)
5.2.5 Beispiele für Bandstrukturen
Zustandsdichte und Bandstrukturen von Kupfer
165
Zustandsdichte und Bandstrukturen von Germanium
5.2.6 Fermi-Flächen
Die Besetzung der elektronischen Zustände bei T=0 ist auf die Zustände für die gilt E ≤ EF
beschränkt. Für quasi-freie Elektronen (d.h. k ≈ 0 oder zumindest weit weg von k = |π/a|)
lässt sich dies auf zustände im k-Raum übertragen:
r
k ≤ kf =
2mEF
~2
(5.107)
mit
~2
EF =
2m
3π 2 N
V
2/3
(5.108)
ergibt sich
kF =
3π 2 N
V
1/3
.
(5.109)
Für ein kubisch flächenzentriertes Gitter gilt:
N
4
= 3
V
a
166
(5.110)
wobei a die Gitterkonstante ist. Somit ergibt sich für kF :
kF =
3π 2
a3
1/3
≈
4, 91
a
(5.111)
Der kürzeste Abstand zum Rand der Brillouin-Zone in einem ffc-Gitter (vom Zentrum zum
Mittelpunkt der Sechsecke) ergibt sich:
kmin =
1 2π √
5, 44
3≈
2 a
a
(5.112)
Dies hätte zur Folge, dass die Fermifläche an keiner Stelle die Grenze der ersten BrillouinZone berührt. Dies ist nicht korrekt, da bei der Überlegung von einem rein quadratischen
Dispersionsrelation ausgegangen wurde. Gerade an der Brillouin-Zonengrenze ist dies aber
nicht korrekt. Hier verflacht die Dispersionsrelation, so dass zu einer bestimmten Energie
größere Wellenzahlen gehören als im quadratischen Fall. Somit berührt die Fermifläche die
Brillouin-Zonengrenze, wie es im folgenden Bild zu sehen ist:
Die Fermi-Fläche von Kupfer
Reicht die Besetzungs“-Kugel über die Brillouin-Zone hinaus, so ergibt sich folgende
”
Situation in zwei Dimensionen:
167
Besitzt ein Atom in einer Elementarzelle mehr als ein Valenzelektron, reicht die erste
Brillouin-Zone nicht mehr aus, um die Elektronen aufzunehmen. Die höheren Brillouin-Zonen
werden wie folgt in zwei Dimensionen konstruiert:
Zu der ersten Brillouin-Zone gehören alle Punkte des k-Raums, die vom Ursprung aus zu
erreichen sind, ohne eine Bragg-Ebene zu überqueren. Zu der zweiten Brillouin-Zone gehören
alle diejenigen Punkte, die man aus der ersten Brillouin-Zonen erreichen kann, indem man nur
eine Bragg-Ebene überquert. Alle weiteren Brillouin-Zonen lassen sich wie folgt konstruieren:
zu den Punkten, die der (n + 1)-Brillouin angehören, gelangt man aus der n-ten BrillouinZone durch überqueren einer Bragg-Ebene und die nicht zur (n − 1) gehören.
4
4
4
4
4 3 2 3 4
34
43
1
2
2
4
4
3
3
4 3 2 3 4
168
Die Aktualität von Untersuchungen an Fermi-Flächen
Die Fermi-Kugel im
erweiterten Zonenschema
Die selbe Situation im reduzierten Zonenschema
Die ersten drei Brillouin-Zonen haben folgende Gestalt für kubisch raumzentrierte (bcc)
und kubisch flächenzentriertes Gitter (fcc):
169
Die Aktualität von Untersuchungen an Fermi-Flächen
Die Fermi-Fläche von Strontiumruthinat
Physics Today January
2001
170
5.2.7 Boltzmann-Transportgleichung
Im Folgenden soll kurz die formale Beschreibung eines Ladungstransports betrachtet werden.
Man geht von folgenden Annahmen aus:
• Elektronen können als Fermiionen im Gleichgewicht beschrieben werden
• Energie- und Wellenzahlverteilung sind durch das angelegte äußeres Feld nur wenig
verändert.
• es gilt also f0 (E(~k)) =
1
E−EF
e kB T
+1
• das externe Feld verursacht eine Störung f = f0 + δf
Betrachten wir die Verteilungsfunktion f (~r, ~v ), die von dem Ort und von der Geschwindigkeit abhängig ist. Das Integral der Verteilungsfunktion über den gesamten Raum und alle
Geschwindigkeiten ergibt die gesamte Teilchenzahl. Da diese natürlich unter dem Einfluss
äußere Felder erhalten bleibt, wird sich die Verteilungsfunktion durch diese Felder ändern
aber das Integral nicht. Ohne jegliche Energieverluste muss nach dem Satz von Liouville für
die Entwicklung der Verteilungsfunktion im sechs-dimensionalen Phasenraum gelten:
f (t + dt, ~r + δ~r, ~v + δ~v ) = f (t, ~r, ~v )
(5.113)
Lässt man Stöße zu, so reduziert sich das Phasenraumvolumen in der Zeit gerade durch den
Einfluss der Stöße:
∂f
(5.114)
f (t + dt, ~r + δ~r, ~v + δ~v ) − f (t, ~r, ~v ) = dt
∂t Stöße
Somit lässt sich schreiben:
∂f
∂f
dt
+ d~r∇~r f + d~v ∇~v f = dt
∂t
∂t Stöße
und in differentieller Darstellung, wenn man a = F/m = dv/dt ansetzt:
∂f
∂f
+ v∇~r f + a∇~v f =
.
∂t
∂t Stöße
(5.115)
(5.116)
Dies wird als Boltzmann-Transportgleichung bezeichnet. Sie lässt sich als eine Kontinuitätsgleichung im Phasenraum auffassen. Nun lässt sich der Stoßterm als einfache Relaxation des
Elektronensystems Richtung Gleichgewichtslage f0 nähern:
∂f
f − f0
=−
.
(5.117)
∂t Stöße
τc
Somit ergibt sich für eine Verteilung die durch ein externes elektrisches Feld aus der Gleichgewichstlage gebracht wurde nachdem das externe Feld abgeschaltet wurde:
∂(f − f0 )
f − f0
=−
.
∂t
τc
171
(5.118)
Für diese Differentialgleichung ergibt sich die Lösung:
(f − f0 )(t) = (f − f0 )|t=0 exp
t
τc
.
(5.119)
Somit ergibt sich für die Boltzmann-Transportgleichung in Relaxationszeitnäherung, wobei
im stationären Zustand per Definition ∂f
∂t = 0 gilt:
∂f
∂t
+ v∇~r f + a∇~v f = −
f − f0
.
τc
(5.120)
Durch das externe Feld verschiebt sich die Fermi-Kugel im k-Raum. Dabei besteht der folgende Zusammenhang zwischen angelegtem elektrischen Feld, Relaxationszeit und Verschiebung
im k-Raum:
δkx =
−eτ Ex
~
(5.121)
Die Relaxationszeit hat in Metallen im wesentlichen zwei Beiträge:
1. Streuung an Phononen
2. Streuung an Gitterstörstellen
1
1
1
=
+
τ
τP h (T ) τSt
Dabei ist der Beitrag durch die Streuung an Phononen temperaturabhängig.
172
(5.122)
Widerstand von Na
Widerstand von
Cu-Legierungen
5.2.8 Thermoelektrische Effekte
Bisher haben wir bei der Betrachtung der Boltzmann-Transportgleichung keine Temperaturgradienten berücksichtigt (∇T = 0). Im Folgenden sollen die sich ergebenden Konsequenzen
für ∇T 6= 0 betrachtet werden.
Im stationären Fall Ė = 0, ∂(∇∂t~r T ) = 0 und ∂f
∂t = 0 folgt für die Nichtgleichgewichtsver∂f
~
teilung mit ∇~r f [k, T (~r)] = ∂T ∇~r T und unter der Annahme kleiner Abweichungen von der
Gleichgewichtsverteilung (Linearisierung):
∂f0
e
~v · ∇~r T.
(5.123)
f (~k) ≈ f0 (~k) + τ E · ∇~k f0 − τ
~
∂T
Daraus folgt für den Stromfluss, wenn ein elektrisches Feld in x-Richtung angelegt wird:
Z
~j = − e
v(~k)f (~k)d~k
8π 3
Z
Z
Z
eτ (~k) ~
∂f0 ~
∂f0 2
e
e
e
~
~
~
v(k)Ex
dk + 3 τ
~v · ∇~r T d~k
= − 3 v(k)f0 (k)dk − 3
8π
8π
~
∂kx
8π
∂T
|
{z
}|
{z
}
=0
=σE
x
Z
e
∂f0 2
= σEx + 3 τ
~v · ∇~r T d~k.
(5.124)
8π
∂T
Für die Fälle von isotropen Medien und kubischen Kristallen verschwinden die y- und zKomponenten des Stromes. Da f (~k) inversionssymmetrisch zum Ursprung (~k = 0) ist, fällt
das Integral über vx f0 weg.
~j = 0
drei Fälle:
1. Wir
Fallbetrachten
1
Ex =
σ
Z
τ
173
∂f0 2
~v · ∇~r T d~k
∂T
(5.125)
Bei verschwindend kleinem Strom stellt sich durch den Temperaturgradienten ∇~r T ein
elektrisches Feld ein. Dieser Effekt wird Seebeck-Effekt genannt.
~ ≈0
2. Fall |E|
~j = −
Z
τ
∂f0 2
~v · ∇~r T d~k
∂T
(5.126)
Bei verschwindend elektrischen Feld stellt sich durch den Temperaturgradienten ∇~r T
ein elektrischer Strom ein. Dieser Effekt wird Peltier-Effekt genannt.
3. Fall Der Effekt der Kopplung von elektrischer und Wärmestromdichte in Anwesenheit
eines Temperaturgradienten, wird Thomson-Effekt genannt.
174
6 Halbleiter
6.1 Banddiagramme und Energielücken
Banddiagramm von Silizium
Banddiagramm von Germanium
175
Beide Materialien sind so genannte indirekte Halbleiter.
Für das Verständnis der Richtung vergleiche Seite 106.
Banddiagramm von Galliumarsenid
Galliumarsenid ist ein direkter Halbleiter.
Werte der Bandlücke für die gebräuchlichsten Halbleitermaterialien
Eg (T = 0K)[eV ] Eg (T = 300K) [eV]
Si
1,17
1,12
Ge
0,75
0,67
GaAs
1,52
1,43
GaSb
0,81
0,7
InSb
0,24
0,18
InAs
0,43
0,35
InP
1,42
1,35
Durch die Beziehung:
~2 k 2
E(~k) =
(6.1)
2m
motiviert, lässt sich aus der Krümmung im Banddiagramm eine effektive Masse angeben.
Dabei wird der Verlauf des Bands durch eine Parabel angenähert.
1
1 ∂E 2
=
m∗
~2 ∂~k 2
(6.2)
Die effektive Masse wird üblicherweise auf die Masse des freien Elektrons bezogen. Die
effektiven Massen sind im Allgemeinen richtungsabhängig. Die effektive Masse entlang den
176
Hauptachsen ([100] bei Silizium und [111] bei Germanium) werden als longitudinale effektive
Masse bezeichnet, während sie in den orthogonalen Richtungen als transversal bezeichnet
werden.
Si
Ge
m∗t /m
0,19
0,082
m∗l /m
0,92
1,57
6.1.1 Zyklotronresonanz
Die effektive Massen werde mit der Methode der Zyklotronresonanz gemessen. Betrachtet
man ein Elektron am Leitungsbandminimum, lässt sich seine Energie entwickeln:
~2 X
E(~k) = EL +
kµ (M −1 )µν kν
2 µν
(6.3)
~ an,
wobei EL die Energie an der Leitungsbandunterkante ist. Legt man ein Magnetfeld H
so folgt aus den semiklassischen Bewegungsgleichungen für die Entwicklung des Ortes ~r und
die Änderung des Impulses ~~k:
1 ∂E(~k)
,
~ ∂~k
1
˙
~
~~k = (−e) ~v (~k) × H
c
und damit muss die Geschwindigkeit ~v (~k) die folgende Gleichung erfüllen:
~r˙ =
~ d~v = ∓ e ~v × H.
~
M
dt
c
Diese Gleichung führt auf eine Schwingungslösung:
~v = <(~v0 )e−iωt
(6.4)
(6.5)
(6.6)
(6.7)
setzt man für die Kreisfrequenz an:
eH
(6.8)
m∗ c
dabei ist m∗ die Zyklotronmasse für den Fall, dass das Magnetfeld entlang der z-Richtung
angelegt wurde:
r
det M
∗
m =
(6.9)
Mzz
Oder mit Hilfe des Massetensors ausgedrückt:
s
m1 m2 m3
∗
m =
.
(6.10)
2
Ĥ1 m1 + Ĥ22 m2 + Ĥ32 m3
ω=
Dabei sind Ĥi die Komponenten eines dem magnetischen Feld parallelen Einheitsvektors.
Im folgenden Bild ist das Resultat eine Messung an Silizium bei einer eingestrahlten Frequenz von 24GHz dargestellt. Es ist die Absorption über dem Magnetfeld aufgetragen.
177
6.2 Ladungsträgerdichte im intrinsischen Halbleiter
Unter intrinsischen Halbleitern versteht man ideales Material, das keinerlei Verunreinigungen durch andere Elemente aufweist. In diesen Materialien kann nur Stromleitung dadurch
zustande kommen, dass Elektronen aus dem Valenzband in das Leitungsband stattfindet.
Bei Halbleitern tragen nicht nur die über die Bandlücke angeregten Elektronen im Leitungsband zur Leitfähigkeit bei, sondern auch durch die Anregung entstandenen Lücken —
so genannte Löcher. Damit ergibt sich für die Leitfähigkeit:
σ = |e|(nµn + pµp )
(6.11)
wobei n und p die Konzentration von Elektronen und Löchern während µn und µp die
Beweglichkeit von Elektronen und Löchern angibt.
Die Konzentrationen von Elektronen und Löchern lassen sich wie folgt bestimmen:
Z ∞
n =
DL (E)f (E, T )dE
(6.12)
EL
EV
Z
DV (E)[1 − f (E, T )]dE
p =
(6.13)
−∞
Für den Fall parabolischer Näherung, d.h. m∗ = const. ergibt sich für die Zustandsdichten
D mit Gleichung (5.34):
DL (E) =
DV (E) =
(2m∗n )3/2 p
E − EL ,
2π 2 ~3
(2m∗p )3/2 p
EV − E,
2π 2 ~3
178
(E > EL );
(6.14)
(E < EV )
(6.15)
E
E
DL(E)
f(E)DL(E)
EL
EF
EV
f(E)
[1-f(E)]DV(E)
DV(E)
f(E) D(E)
dn
dE
dp
dE
Im verbotenen Band ist die Dichte natürlich gleich Null. Da die Zone in der die FermiEnergie von Eins und Null verschieden ist, d.h. ungefähr von der Größe kB T ist und dies somit
klein gegenüber der Bandlücke ist (∼1eV), lässt sich die Fermi-Verteilung f (E, T ) innerhalb
der Bänder durch die Boltzmann-Besetzungswahrscheinlichkeit annähern, somit ergibt sich
im Fall des Leitungsbandes:
1
e
E−EF
kB T
−
∼e
E−EF
kB T
1
für E − EF 2kB T
(6.16)
+1
Für die Elektronenkonzentration im Leitungsband folgt damit:
Z
(2m∗n )3/2 kEFT ∞ p
− E
n=
e B
E − EL e kB T dE.
2
3
2π ~
EL
(6.17)
Es ergibt sich für die Elektronen- und Lochkonzentration nach einer Substitution und Integration:
2πm∗n kB T
h2
3
EL − EF
E L − EF
L
= Nef
exp
−
exp −
f
kB T
kB T
3
2πm∗p kB T 2
EV − EF
EV − EF
V
p = 2
exp
= Nef f exp
h2
kB T
kB T
n = 2
2
(6.18)
(6.19)
L und N V bezeichnen die effektiven Zustandsdichten. Diese Situation
Die Konstanten Nef
f
ef f
kann so interpretiert werden, dass Leitungsband und Valenzband durch jeweils ein Energieniveau darstellt mit den temperaturabhängigen Zustandsdichten. Die Besetzungsdichte wird
durch den Boltzmann-Faktor bestimmt. Diese Näherung hat häufig Gültigkeit und wird die
179
Näherung der Nichtentartung. Durch starke Dotierung können sehr viele Ladungsträger in den
Halbleiter eingeführt werden, der Halbleiter entartet und somit bricht diese Näherung zusammen. Bildet man das Produkt aus Gl.(6.18) und Gl.(6.19) so ergibt sich mit Eg = EL − EV :
−Eg
np =
L
V
k T
Nef
f Nef f e B
=4
kB T
2π~2
3
3
−Eg
(m∗n m∗p ) 2 e kB T
(6.20)
Hier wird deutlich, dass sich die Konzentrationen von Elektronen und Löcher nach Art eines
Massenwirkungsgesetzes“ einstellen werden, d.h. das Produkt der beiden ist konstant bei
”
einer bestimmten Temperatur. Im Folgenden gehen wir von einem intrinsischen Halbleiter aus,
das heißt, alle freie Elektronen im Leitungsband hinterlassen jeweils ein Loch im Valenzband.
Das hat zur Konsequenz, dass n = p gilt und damit:
n=p=
q
L NV e
Nef
f ef f
−Eg
2kB T
=2
kB T
2π~2
3
2
3
−Eg
(m∗n m∗p ) 4 e 2kB T
(6.21)
Einige Werte für die gebräuchlichsten Halbleitermaterialien bei Zimmertemperatur:
Ge
Si
GaAs
Eg [eV]
0,67
1,1
1,43
ni [cm−3 ]
2, 4 × 1013
1, 5 × 1010
5 × 107
Aus der Ladungsneutralität in intrinsischen Halbleitermaterialien lässt sich das Fermi-Niveau
ableiten:
E
EV
E
E
− k LT k FT
− k FT
L
V
k T
n = p = Nef
(6.22)
f e B e B = Nef f e B e B
auflösen nach den Exponentialfunktionen in EF liefert:
e
2EF
kB T
=
V
Nef
f
L
Nef
f
e
EV +EL
kB T
(6.23)
somit ergibt sich für das Fermi-Niveau und schließlich mit den Gln. (6.18) und (6.19):
!
∗
V
Nef
mp
EV + EL kB T
EV + EL 3
f
EF =
+
ln
=
+ kB T ln
(6.24)
L
2
2
2
4
m∗n
Nef f
Sind effektive Zustandsdichten oder effektive Massen gleich liegt das Fermi-Niveau genau in
der Bandmitte. Dies ist im Allgemeinen natürlich nicht der Fall, wodurch sich eine Asymmetrie
ergibt und das Fermi-Niveau schwach temperaturabhängig ist.
6.3 Dotierung von Halbleitern
Durch zusätzliches Einfügen von Atomen der dritten oder vierten Hauptgruppe ergibt sich ein
Überschuss oder ein Defizit an Elektronen. In diesem Fall spricht man von einem dotierten
Halbleiter. Wird ein Atom der dritten Hauptgruppe (Br, Al, Ga, In, T l) eingefügt spricht
180
man von einer Akzeptordotierung. Da hier ein Elektron fehlt um alle Bindungen abzusättigen,
entsteht hier eine Stelle im Kristall, die bevorzugt Elektronen aufnehmen (akzeptieren) wird.
Wird hingegen mit Atomen der fünften Hauptgruppe (P, As, Sb, Bi) dotiert, ist pro Atom
ein Elektron nicht in der Lage eine Bindung einzugehen und somit kann dieses Elektron leicht
durch den Kristall wandern. Hier spricht man von einem Donator.
Si Si Si Si Si
Si Si Si Si Si
Si Si Si Si Si
Si Si P Si Si
Si Si Si Si Si
Si Si Si Si Si
Si Si Si Si Si
Si Si Si Si Si
Si Si Si Si Si
n-dotiertes Silizium
p-dotiertes Silizium
Si Si B Si Si
Durch das Dotieren werden neue Energieniveaus in der Bandlücke erzeugt, die je nach Charakter der Dotierung näher am Valenzband (Akzeptoren) oder näher am Leitungsband (Donatoren) sind.
Elektronenenergie E
n-Halbleiter
Ed
p-Halbleiter
EL
ED
EL
Ea
EV
Ei
x
ED
EV
x
Einige exemplarische Werte für Störstellenniveaus für Silizium und Germanium:
Si
Ge
P [meV]
44
12
Donatoren
As [meV] Sb [meV]
49
39
12,7
9,6
181
Bi [meV]
69
–
Si
Ge
B [meV]
45
10,4
Akzeptoren
Al [meV] Ga [meV]
67
74
10,2
10,8
In [meV]
153
11,2
Tl [meV]
260
10
Die Störstellenverteilung lässt sich recht gut durch spektroskopische Methoden bestimmen.
Das folgende Bild zeigt das Absorptionsspektrum von einem Antimon dotierten Germaniumkristall.
6.3.1 Ladungsträgerdichten in dotierten Halbleitern
182
Elektronenenergie E
EL
ED
+
D
N
EA
EV
0
ND=ND
-
0
D
N
NA- NA0
+
n
-
-
-
p
+
+
0
NA=NA
x
Dabei bezeichnen:
ND die Dichte aller vorhandenen Donatoren,
+
ND
die Dichte der positiv geladenen Donatoren,
0 die Dichte der ungeladenen Donatoren,
ND
NA die Dichte aller vorhandenen Akzeptoren,
NA− die Dichte der negativ geladenen Akzeptoren und
NA0 die Dichte der ungeladenen Akzeptoren.
Es lässt sich ausgehend vom Massenwirkungsgesetz“ Gl.(6.20) und unter Ausnutzung der
”
Ladungsneutralität zeigen, dass sich für die Elektronenkonzentration folgendes ergibt:
2ND
n≈
r
1+
Ed
1+
(6.25)
4 NNLD e kB T
ef f
Für diese Gleichung lassen sich drei Temperaturbereiche unterscheiden:
1. Für niedrige Temperaturen wenn
4
ND kEdT
e B 1
L
Nef
f
(6.26)
gilt, dann ergibt sich:
n≈
q
Ed
BT
− 2k
L e
ND Nef
f
(6.27)
In diesem Bereich sind noch nicht alle Störstellen ionisiert, so dass bei jeder Temperaturerhöhung weitere Störstellen ionisiert werden können. Man spricht hier von einer
Störstellenreserve.
183
2. Für mittlere Temperaturen bei denen gilt
ND kEdT
e B 1
L
Nef
f
(6.28)
n ≈ ND = const.
(6.29)
4
gilt, dann ergibt sich:
Hier sind alle Störstellen ionisiert und die Konzentration von Ladungsträger bleibt in
einem Temperaturbereich konstant.
3. Für hohe Temperaturen wenn Elektronen genügend thermische Energie besitzen um
die Energielücke zu überwinden, dann verhält sich der Halbleiter wie ein intrinsischer
Halbleiter.
Schematische Darstellung der Ladungsträgerdichten in den unterschiedlichen Bereichen
E
EL
ED
Ei
Erschöpfung
intrinsisch
log n
Steigung -Eg/2kB
Steigung -Ed/2kB
Reserve
Ed
Fermi-Niveau EF(T)
EV
reziproke Temperatur T-1
184
Eg
Die Ladungsträgerdichte für Germanium mit unterschiedlichen Donatorkonzentrationen
(1018 bis 1013 cm−3 , Proben (1) bis (6))
6.4 Leitfähigkeit von Halbleitern
Für den Zusammenhang zwischen Stromdichte und elektrischen Feld lässt sich angeben:
~
~j = e(nµn + pµp )E
(6.30)
Hier bezeichnen µn und µp die Elektronen- bzw. die Löcherbeweglichkeit. Unter Anwendung
der Näherung für nichtentarteten Halbleitern und somit der Verwendung der BoltzmannStatistik ergibt sich für die Elektronenbeweglichkeit:
µn =
1 hτ (~k)v 2 (~k)i
e.
m∗n hv 2 (~k)i
(6.31)
v(~k) und τ (~k) bezeichnet die Geschwindigkeit und die Relaxationszeit an einem bestimmten
Punkt im k-Raum. Es folgt, dass die Beweglichkeit proportional zur Relaxationszeit τ ist.
Für die Streurate, d.h. den Kehrwert der Relaxationszeit, lässt sich schreiben:
1
∝ hviΣ
(6.32)
τ
185
Σ bezeichnet den Streuquerschnitt für Elektronen und Löcher an einem Streuzentrum. Wegen
der Boltzmann-Statistik gilt im Halbleiter:
hvi ∝
√
T.
(6.33)
Es lassen sich zwei wesentliche Streumechanismen feststellen:
1. Streuung an akustischen Phononen; dabei gilt ΣP h ∝ T und damit ergibt sich mit
Gl.(6.32) und Gl.(6.33):
3
µph ∝ T − 2
(6.34)
2. Streuung an geladenen Störstellen; dabei gilt Σst ∝ hvi−4 und mit hvi ∝
sich mit Gl.(6.32) und Gl.(6.33):
1
Nst
∝ 3
τSt
T2
√
T ergibt
(6.35)
Damit ergibt sich für die Beweglichkeit
3
µSt ∝ T 2
log m
Streuung an
ionisierten
Störstellen
~T
(6.36)
Streuung an
Phononen
~T
3/2
log T
186
-3/2
Die Ladungsträgerbeweglichkeit für Germanium mit unterschiedlichen
Donatorkonzentrationen
(1018 bis 1013 cm−3 , Proben (1) bis (6))
187
Die Leitfähigkeit für Germanium mit unterschiedlichen Donatorkonzentrationen
(1018 bis 1013 cm−3 , Proben (1) bis (6))
Die Driftgeschwindigkeit für verschiedene Halbleiter
188
6.5 Der pn-Übergang
Bringt man ein p- und ein n-dotiertes Material in elektrischen Kontakt werden Elektronen
vom n-dotierten Material in das p-dotierte fließen, bis sich das Fermi-Niveau (das chemische
Potential) in beiden Materialien so angeglichen haben, dass dies keine Gradienten mehr aufweist. Dadurch bildet sich eine so genannte Raumladungszone aus. Diese Raumladungszone
führt zu einem Driftstrom, der den Diffusionsstrom kompensiert, so dass im Gleichgewicht
keine effektiver Strom mehr fließt.
Schema des pn-Übergangs
Energiebänder des pn-Übergangs ohne und
mit dem Kontakt
189
Raumladungszone und
Ladungsträgerkonzentrationen
6.5.1 Der pn-Übergang im thermischen Gleichgewicht
Jedem Punkt im Kristall lässt sich ein elektrisches Potential zuordnen, für das die PoissonGleichung erfüllt sein muss:
∂ 2 V (x)
%(x)
=−
(6.37)
2
∂x
εε0
Elektronen werden in einem p-dotierten Material als Minoritätsladungsträger und Löcher
in diesem Material als Majoritätsladungsträger. Entsprechendes gilt in n-dotierten Material:
Löcher sind Minoritätsladungsträger und Elektronen Majoritätsladungsträger. So sind die in
der Raumladungszone befindlichen Ladungsträger Minoritätsladungsträger, da sie aus dem
entsprechend dotierten Material in das gegenüberliegende diffundieren.
Für die Majoritätsladungsträger lässt sich schreiben:
L
n −E
EL
F
kB T
(6.38)
p
E −E
− Fk T V
B
(6.39)
−
nn = Neff e
V
pp = Neff
e
Die Indizes n und p geben an wie das Material dotiert ist, in dem die Größe betrachtet wird.
Außerdem lässt sich schreiben:
n2i
V
L
−
= nn pn = Neff Neff e
n −E n
EL
V
kB T
(6.40)
Damit kann die sich maximal einstellende Diffusionsspannung VD , welche der maximalen
Differenz des Makropotentials entspricht, mit der Ladungsträgerkonzentration in Verbindung
gebracht werden:
pp n n
p
n
eVD = −(EV − EV ) = kB T ln
(6.41)
n2i
190