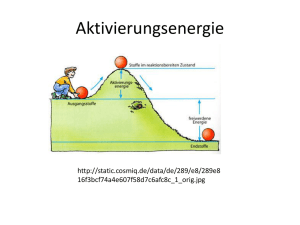
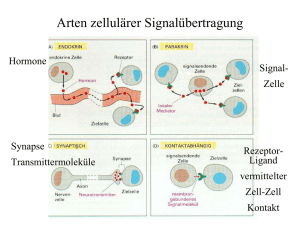
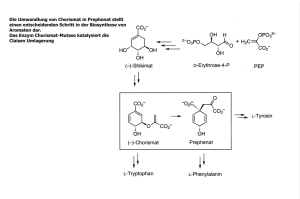
Reaktionskinetik

Reaktionskinetik
Maximilian Erlacher
Quelle: Mathematical Biology: I. An Introduction, Third
Edition J.D. Murray Springer
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Basisenzymreaktion
Enzym:
• Protein mit katalytischen Effekt
• wirkt nur auf genau einen Stoff
• wirkt hemmend oder aktivierend
• liegt in niedriger Konzentration vor
Basisenzymreaktion
• S=
ˆ # Ausgangsstoff
• E=
ˆ # Enzym
• SE =
ˆ # Zwischenzustand
• P=
ˆ # Produkt
k1
k
S + E SE →2 P + E
k−1
ki Reaktionsraten
Basisenzymreaktion
Folgende Differentialgleichungen lassen sich aus den
Änderungsraten herauslesen, wenn wir die Konzentrationen
s = [S], e = [E], c = [SE], p = [P] betrachten:
ds
dt
de
dt
dc
dt
dp
dt
= −k1 es + k−1 c,
= −k1 es + (k−1 + k2 )c,
= k1 es − (k−1 + k2 )c,
= k2 c,
Anfangswerte
s(0) = s0 , e(0) = e0 , c(0) = 0, p(0) = 0.
Basisenzymreaktion
• p entkoppelt
• verkürzen mit e(t) + c(t) = e0 System auf
ds
dt
dc
dt
= −k1 e0 s + (k1 s + k−1 )c,
= k1 e0 s − (k1 s + k−1 + k2 )c,
Basisenzymreaktion
Vergleich s und c nicht anschaulich!
s0
0
s
c
t
Basisenzymreaktion: Entdimensionalisierung
• s und c Entdimensionalisierung klar: Betrachte u im
Verhältnis zu s/s0 , v im Verhältnis zu c/e0
• Entdimensionalisierung von t nicht trivial,
• tc , Entwicklung von c
• ts , Entwicklung von s
Basisenzymreaktion: Entdimensionalisierung
• s und c Entdimensionalisierung klar: Betrachte u im
Verhältnis zu s/s0 , v im Verhältnis zu c/e0
• Entdimensionalisierung von t nicht trivial,
• tc , Entwicklung von c
• ts , Entwicklung von s
• Setze
K =
k−1 + k2
Km
=
k1 s0
s0
Km nennt man die Michaelis-Konstante
Basisenzymreaktion: Entdimensionalisierung
Standard Entdimensionalisierung
τ = k1 e0 t,
u(τ ) =
s(t)
,
s0
v (τ ) =
c(t)
,
e0
wir erhalten
du
dτ
dv
ε
dτ
= −u + (u + K − λ)v ,
= u − (u + K )v ,
u(0) = 1,
v (0) = 0.
ε=
c0
,
s0
Basisenzymreaktion: Entdimensionalisierung
[C]
1
steigt in wenigen Sekunden sehr stark
2
bis Ausgleichszustand
3
danach gemäßigtes abklingen
Aus
dc
= k1 e0 s0 − k1 (s0 + Km )c
dt
wähle Zeitskalierung
tc =
1
k1 (s0 + Km )
Basisenzymreaktion: Entdimensionalisierung
Annahme, e s ⇒ dc/dt ≈ 0
⇒ c(t) =
somit
weshalb wir
ds
k2 e0 s
=−
,
dt
s + Km
s0
ts ≈ ds dt max
wählen.
e0 s
,
s + Km
≈
s0 + Km
,
k2 e0
Basisenzymreaktion: Entdimensionalisierung
Zeitskalierung
τ=
t
,
tc
liefert
du
dτ
dv
dτ
= ε −u +
σ
ρ
uv +
v ,
1+σ
(1 + σ)(1 + ρ)
σ
v
= u−
uv −
,
1+σ
1+σ
mit
u(0) = 1,
v (0) = 0.
Basisenzymreaktion: Entdimensionalisierung
Zeitskalierung
T = (1 + ρ)t/ts = ε(1 + ρ)k2 t.
Dadurch
du
dT
dv
ε
dT
= −(1 + σ)u + σuv +
= (1 + σ)u − σuv − v .
ρ
v,
1+ρ
Basisenzymreaktion: Veranschaulichung
Schemenhafter Verlauf des entdimensionalisierten Systems,
wenn ε 1
1
e/e0 = 1 − v
0
v
u
τ
Abbildung : Mathematical Biology: I. An Introduction,
Third Edition J.D. Murray Springer
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Michaelis-Menten-Analyse
Ansatz zum Lösen der Differentialgleichungen durch
Taylorentwicklung
X
X
u(τ, ε) =
εn un (τ ), v (τ, ε) =
εn vn (τ ).
n=0
n=0
Einsetzen in die bisherigen Differentialgleichungen liefert
Sequenz von Differentialgleichungen für un (τ ) und vn (τ ).
Michaelis-Menten-Analyse
Die Gleichungen der Ordnung 1:
du0
= −u0 + (u0 ) + K − λ)v0 ,
dτ
u0 (0) = 1,
0 = u0 − (u0 + K )v0 ,
v0 (0) = 0.
• Anfangsbedingungen nicht erfüllt.
• Lösungen für die weitere Entwicklung von u und v
interessant.
Michaelis-Menten-Analyse
Lösung ist:
v0 =
u0
u0 + K
⇒
du0
u0
= −λ
dτ
u0 + K
und damit
u0 (τ ) + K ln(u0 (τ )) = A − λτ.
Michaelis-Menten-Analyse
gute Lösung für kleine τ substituiere
σ=
τ
,
ε
u(τ, ε) = U(σ, ε),
v (τ, ε) = V (σ, ε).
Dies führt zu
dU
dσ
dV
dσ
= −εU + ε(U + K − λ)V ,
= U − (U + K )V ,
U(0) = 1, V (0) = 0.
Michaelis-Menten-Analyse
Gleichungen der Ordnung 1:
dU0
= 0,
dσ
dV0
= U0 − (U0 + K )V0 .
dσ
Lösungen sind
U0 (σ) = 1,
V0 (σ) =
1
(1 − exp[−(1 + K )σ])
1+K
Gleichungen höherer Ordnungen liefern keine weiteren
Informationen.
Michaelis-Menten-Analyse
Mit den Lösungen aus den O(1)-Gleichungen erhalten wir
somit
u(τ ; ) = u0 (τ ) + O(ε), u0 (τ ) + K log(u0 (τ )) = 1 − λτ,
h
1 τ i
v (τ ; ε) =
1 − exp −(1 + K )
+ O(ε), für 0 < τ 1
1+K
ε
u0 (τ )
+ O(), für 0 < ε τ.
=
u0 (τ ) + K
Die Lösungen gelten demnach nur für kleine ε, was in der
Reaktionskinetik aber üblich ist.
Michaelis-Menten-Analyse
Anfangsgeschwindigkeit r0 der Reaktion, zur Abschätzung wie
schnell innere in die äußere Lösung umschlägt:
du0 (τ )
u0 (0)
λ
r0 =
=λ
=
.
dτ
u0 (0) + Km
1+K
τ =0
Rücksubstitution r0 ∼ v
v=
k2 e0 s0
Vmax s0
=
.
s0 + K
s0 + Km
Michaelis-Menten-Analyse
Michaelis-Konstante Km =
ˆ Halbwertszeit
Abbildung : Wikipedia
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Selbstauslöschende Kinetik
• S=
ˆ # Ausgangsstoff
• E=
ˆ # Enzym
• Ei =
ˆ # inaktives Enzym
• X, Y=
ˆ # Zwischenzustand
• P=
ˆ # Produkt
k1
k
k
E + S X →2 Y →3 E + P,
k−1
k
Y →4 Ei .
Anfangsbedingungen
E(0) = e0 ,
S(0) = s0 ,
X (0) = Y (0) = Ei (0) = P(0) = 0.
Selbstauslöschende Kinetik
• [E] gegeben durch [E] = e0 − [X ] − [Y ] − [Ei ]
Selbstauslöschende Kinetik
• [E] gegeben durch [E] = e0 − [X ] − [Y ] − [Ei ]
• [P] ist entkoppelt
Selbstauslöschende Kinetik
• [E] gegeben durch [E] = e0 − [X ] − [Y ] − [Ei ]
• [P] ist entkoppelt
Dies führt zu:
d[S]
dt
d[X ]
dt
d[Y ]
dt
d[Ei ]
dt
= −k1 (e0 − [X ] − [Y ] − [Ei ])[S] + k−1 [X ],
= k1 (e0 − [X ] − [Y ] − [Ei ])[S] − (k−1 + k2 )[X ],
= k2 [X ] − (k3 + k4 )[Y ],
= k4 [Y ].
Selbstauslöschende Kinetik
• Innere Lösungen werden wie bei Michaelis-Menten
bestimmt:
1
2
Mit tc entdimensionalisieren
Potenzreihenansatz so weit entwickeln, bis man keine
konstanten Lösungen erhält.
• Äußere Lösungen entdimensionalisierte mit ts
für ei ergibt sich insbesondere
dei
=φ·y
dT
Selbstauslöschende Kinetik
Entwicklung kann zwei Formen annehmen
1
Enzym wird vollständig inaktiviert.
2
Ausgangsstoff wird vollständig abgebaut.
Modellierungsannahmen
1
φ = O(1).
2
φ = O(ε).
Selbstauslöschende Kinetik
Lösungen für s und ei sind
1
im Fall φ = O(1):
s(0) (T ) =
2
1−β
1 − βe
,
T [1−(1/β)]/(1+ρ)
ei(0) (T ) =
1 − s(0)
.
β
im Fall φ = O(ε):
s(0) (T ) = e−T /(1+ρ) ,
ei(0) = 0,
εei(1) (T ) =
1 − e−T /(1+ρ)
.
β
Selbstauslöschende Kinetik
Abbildung : Mathematical Biology:I. An Introduction,Third Edition J.D.
Murray Springer
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Kooperatives Auftreten
• Viele Enzyme haben mehr als eine Bindungsmöglichkeit
• Erythrozyten können bis zu 4 O2 binden.
• Eine solche Bindung nennt man kooperativ
• Ausgangsstoffe, die die Aktivität eines Enzyms erhöhen
nennt man Aktivator und im anderen Fall Inhibitor
Kooperatives Auftreten
• S=
ˆ # Ausgangsstoff
• E=
ˆ # Enzym mit zwei bindenden Seiten
• C1 , C2 =
ˆ # Zwischenzustand
• P=
ˆ # Produkt
k1
k
S + E C1 →2 E + P,
k−1
k3
k
S + C1 C2 →4 C1 + P,
k−3
mit Anfangswerten
[S](0) = s0 ,
[E](0) = e0 ,
[C1 ](0) = [C2 ](0) = [P](0) = 0.
Kooperatives Auftreten
• p ist entkoppelt von dem System,
• e = e0 − c1 − c2 ,
• Für den Rest ergibt sich
ds
dt
dc1
dt
= −k1 e0 s + (k−1 + k1 s − k3 s)c2 + (k1 + k−3 )c2 ,
= k1 e0 s − (k−1 + k2 + k1 s + k3 s)c1
+(k−3 + k4 − k1 s)c2 ,
dc2
dt
= k3 sc1 − (k−3 + k4 )c2 .
Kooperatives Auftreten
• Standardentdimensionalisierung mit u ∼ s, v1 ∼ c1 und
v2 ∼ c2 und gehen Michaelis-Menten-Verfahren durch.
• O(1)-Gleichungen liefern nichtkonstante Lösungen
v2 =
a3 uv1
,
a4 + a5
v1 =
u
a1 + a2 + u + a3 u 2 (a4 + a5 )−1
Demnach v1 = v1 (u), v2 = v2 (u) und somit
du
dτ
= f (u, v1 (u), v2 (u))
a2 + a3 a5 u(a4 + a5 )−1
a1 + a2 + u + a3 (a4 + a5 )−1 u 2
= −r (u) < 0
= −u
Kooperatives Auftreten
Damit ergibt sich für die anfängliche Rektionsgeschwindigkeit
R0
ds k2 Km0 + k4 s0
= e0 s0
R0 (s0 ) = dt t=0
Km Km0 + Km0 s0 + s02
mit
Km0 =
k4 + k−3
.
k3
Kooperatives Auftreten
Abbildung : Mathematical Biology: I. An Introduction, Third Edition
J.D. Murray Springer
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Autokatalyse, Aktivierung und Inhibition
Autokatalyse ist ein Prozess, bei dem ein Stoff bei seiner
eigenen Produktion beteiligt ist. Beispielsweise hat
k1
A + X 2X
k−1
den Gleichgewichtszustand xS =
Konzentration [A].
k1 a
k−1
bei konstanter
Mit diesem Modell hat man eine dynamische Regulierung des
Stoffes X .
Autokatalyse, Aktivierung und Inhibition
Nun wird X zum Bilden eines anderen Stoffes benötigt
k1
A + X 2X ,
k−1
k
B + X →2 C
Unter der Annahme, dass [A] und [B] konstant sind
• ist xS = 0 stabil, wenn k1 a − k2 b ≤ 0
• ist xS = (k1 a − k2 b)/k−1 stabil, wenn k1 a − k2 b > 0
Autokatalyse, Aktivierung und Inhibition
Betrachten wir nun
k
A + X →1 2X ,
k
X + Y →2 2Y ,
k
Y →3 B,
wobei wir erneut annehmen, dass [A] konstant ist.
Wir erhalten die DGLen
dx
= k1 ax − k2 xy ,
dt
dy
= k2 xy − k3 y ,
dt
von denen wir aber keine stabilen Gleichgewichtspunkte
bekommen.
Autokatalyse, Aktivierung und Inhibition
Modellierungsänderung! Wir wollen
• u aktiviert v .
• Umso größer v , desto kleiner die u-Produktion.
• Das ist rückwirkende Inhibition.
betrachte
du
dτ
dv
dτ
=
a
− c · u = f (u, v ),
b+v
= d · u − e · v = g(u, v ).
a, b, c, d, e > 0 konstant
Autokatalyse, Aktivierung und Inhibition
Modellierungsänderung! Wir wollen
• u aktiviert v .
• Umso größer v , desto kleiner die u-Produktion.
• Das ist rückwirkende Inhibition.
betrachte
du
dτ
dv
dτ
=
a
− c · u = f (u, v ),
b+v
= d · u − e · v = g(u, v ).
a, b, c, d, e > 0 konstant
Autokatalyse, Aktivierung und Inhibition
Gleichgewichtspunkte (u0 , v0 ):
f (u0 , v0 ) = g(u0 , v0 ) = 0,
v0 =
du0
,
e
u02 +
ebu0 ae
−
= 0.
d
cd
Die Punkte stabil nach Analyse der Jacobi-Matrix von
f
g
.
Autokatalyse, Aktivierung und Inhibition
Thomas-Mechanismus
• Reaktion von Sauerstoff v mit Harnstoff u unter dem
Enyzm Uricase.
• entdimensionalisierte Gestalt:
du
dt
dv
dt
= a − u − ρR(u, v ) = f (u, v ),
= α(b − v ) − ρR(u, v ) = g(u, v ),
R(u, v ) =
uv
,
1 + u + Ku 2
a, b, α, ρ, K > 0 konstant.
Autokatalyse, Aktivierung und Inhibition
R ist ein Substratinhibitor
• u klein, R hemmend
• u groß, R aktivierend
Abbildung : Mathematical Biology: I. An Introduction,
Third Edition J.D. Murray Springer
Autokatalyse, Aktivierung und Inhibition
Abhängig von den Parametern können wir mehrere
Gleichgewichtszustände bekommen:
• P1 und P3 linear stabil, wenn die Parameter nicht zu
extrem.
• P2 instabil.
• S erfordert eine genauere Analyse.
Abbildung : Mathematical Biology: I. An Introduction,
Third Edition J.D. Murray Springer
Themen:
1
Basisenzymreaktion
2
Michaelis-Menten-Analyse
3
Selbstauslöschende Kinetik
4
Kooperatives Auftreten
5
Autokatalyse, Aktivierung und Inhibition
6
Mehrfache Gleichgewichtszustände, Mushrooms und
Isolas
Mehrfache Gleichgewichtszustände, Mushrooms
und Isolas
a) Mehrfache Gleichgewichtszustände
b) Mushroom: Ein pilzähnlicher Körper
c) Isolas: Ein isolierter Bereich
Abbildung : Mathematical Biology: I. An Introduction,
Third Edition J.D. Murray Springer
Mehrfache Gleichgewichtszustände, Mushrooms
und Isolas
Modell von Gray und Scott
X + 2Y → 3Y .
entdimensionalisierte System:
du
dt
dv
dt
= a(1 − u) − uv 2 − bu = f (u, v ),
= a(c − v ) + uv 2 + bu − dv = g(u, v ),
a, b, c, d > 0 konstant.
Mehrfache Gleichgewichtszustände, Mushrooms
und Isolas
f (u, v ) = g(u, v ) = 0 liefert
d 2
(a + d)2
2
us (1 + c − us ) = a 1 +
(1 − us ) − bus
.
a
a2
Je nach Parameterwahl erhählt man für us einen der folgenden
Plots:
Abbildung : Mathematical Biology: I. An Introduction,
Third Edition J.D. Murray Springer
Fazit
• Enzymreaktionen haben in der Regel zwei wichtige
Phasen,
• eine, in der das Enzym einsetzt,
• eine, in der der Stoff abgebaut wird.
Fazit
• Enzymreaktionen haben in der Regel zwei wichtige
Phasen,
• eine, in der das Enzym einsetzt,
• eine, in der der Stoff abgebaut wird.
• Analytische Näherungen durch Taylorentwicklung und
Vergleich der beiden Phasen.
Fazit
• Enzymreaktionen haben in der Regel zwei wichtige
Phasen,
• eine, in der das Enzym einsetzt,
• eine, in der der Stoff abgebaut wird.
• Analytische Näherungen durch Taylorentwicklung und
Vergleich der beiden Phasen.
• Modellieren von Reaktionsgleichungen in
unterschiedlichen Situationen,
• selbstauslöschend,
• kooperativ/kontrollierend anderen Enzymen gegenüber,
• selbsterzeugend.
• Verhalten von Gleichgewichtszuständen.
Vielen Dank für ihre
Aufmerksamkeit!