Lösungen

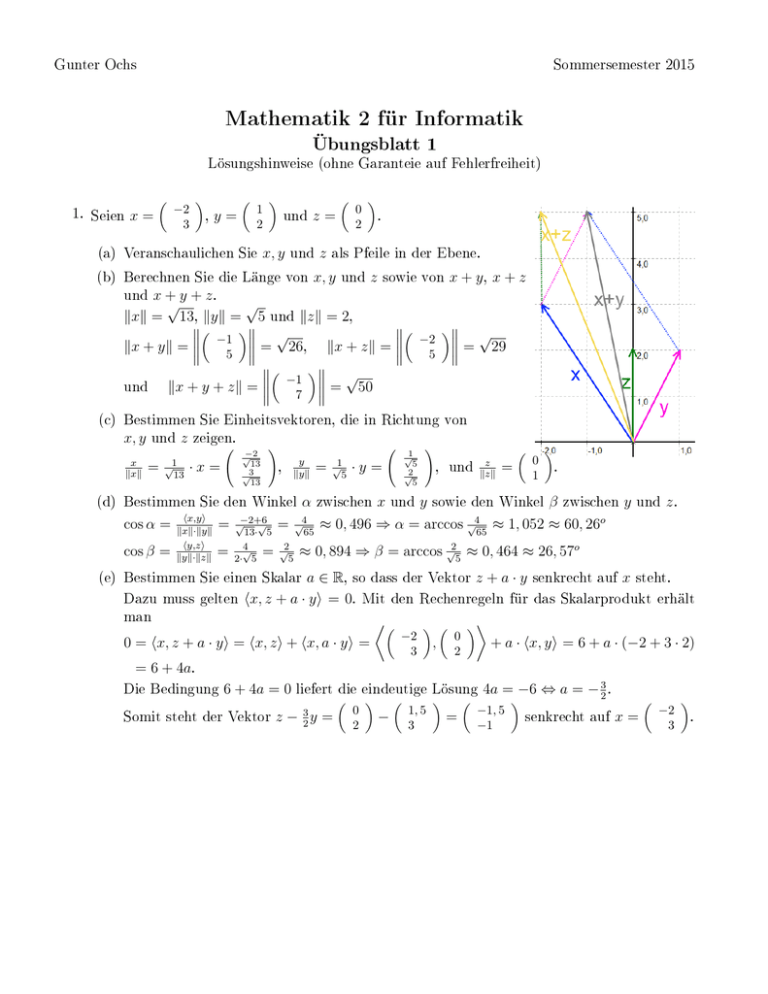
Gunter Ochs
Sommersemester 2015
Mathematik 2 für Informatik
Übungsblatt 1
Lösungshinweise (ohne Garanteie auf Fehlerfreiheit)
1. Seien
x=
−2
3
,
y=
1
2
(a) Veranschaulichen Sie
und
x, y
z=
und
z
0
2
.
als Pfeile in der Ebene.
(b) Berechnen Sie die Länge von
x, y und z sowie von x + y , x + z
x + y + z.
√
√
kxk = 13, kyk = 5 und kzk = 2,
−1 √
−2 √
= 26, kx + zk = = 29
kx + yk = 5 5 −1 √
= 50
und
kx + y + zk = 7 und
(c) Bestimmen Sie Einheitsvektoren, die in Richtung von
x, y
x
kxk
und
=
z
√1
13
zeigen.
−2
√
13
√3
13
·x=
!
,
y
kyk
(d) Bestimmen Sie den Winkel
cos α =
cos β =
hx,yi
kxk·kyk
hy,zi
kyk·kzk
=
=
α
=
√1
5
√1
5
√2
5
·y =
zwischen
x
und
!
z
, und kzk
y
=
0
1
sowie den Winkel
.
β
zwischen
y
und
z.
√ = √4 ≈ 0, 496 ⇒ α = arccos √4 ≈ 1, 052 ≈ 60, 26o
√−2+6
13· 5
65
65
4
2
2
√ = √ ≈ 0, 894 ⇒ β = arccos √ ≈ 0, 464 ≈ 26, 57o
2· 5
5
5
a ∈ R, so dass der Vektor z + a · y senkrecht auf x steht.
hx, z + a · yi = 0. Mit den Rechenregeln für das Skalarprodukt erhält
(e) Bestimmen Sie einen Skalar
Dazu muss gelten
man
0 = hx, z + a · yi = hx, zi + hx, a · yi =
−2
3
,
0
2
+ a · hx, yi = 6 + a · (−2 + 3 · 2)
= 6 + 4a.
Die Bedingung
6 + 4a = 0
Somit steht der Vektor
liefert die eindeutige Lösung
z − 23 y =
0
2
−
1, 5
3
=
4a = −6 ⇔ a = − 32 .
−1, 5
−1
senkrecht auf
x=
−2
3
.
2. Berechnen Sie Seitenlängen und Winkel des Dreiecks im
B = (1; 2; 1)
und
R3
mit den Eckpunkten
A = (0; 1; 1),
C = (1; 0; 3).
Die Seiten sind durch die Vektoren gegeben, die jeweils zwei Eckpunkte verbinden:

 
1
x= 2 −
1
  
1
z = 0 −
3


0
1 =
1


1
2 =
1

1
1 ,
0

0
−2 .
2

y=
  
1
0
 0 − 1 
3
1
Die Seitenlängen sind die Längen der Vektoren
Es ist
hx, yi = 0.
Also stehen
ist ein rechter Winkel
Der Winkel
B
nach
cos β =
A
z
α = 90
im Punkt
γ
=
√ 2√
2· 8
=
im Punkt
γ
und
√
√
2, kyk = 6
und
kzk =
√
8.
senkrecht aufeinander, d. h. der Winkel im Eckpunkt
A
.
=
√2
16
−x
und
=
1
. Es folgt
2
z
(da der Verbindungsvektor von
β = 60o .
kann analog als Winkel
zwischen
√
berechnet werden, man erhält
Alternativ erhält man
y
=

1
 −1 
2
A − B = −x):
√2
2·8
C
und
ist der Winkel zwischen
B
gegeben ist durch
−hx,zi
kxk·kzk
Der Winkel
und
β
x
o
kxk =

cos γ =
3
2
−y
und
−z
und damit zwischen
y
⇒ γ = 30o .
auch über die Winkelsumme im Dreieck (die immer
180o
ist):
γ = 180o − α − β = 30o
4. Zeigen Sie mit Hilfe der Rechenregeln für das Skalarprodunkt:
x, y ∈ Rn gilt
hx + y, x − yi = kxk2 − kyk2 ,
hx + y, x − yi = hx + y, xi + hx + y, −yi = hx, xi + hy, xi − hx, yi + hy, −yi
= hx, xi + hx, yi − hx, yi − hy, yi = hx, xi − hy, yi = kxk2 − kyk2
(a) Für Vektoren
(b) Sind die Vektoren
x und y gleich lang (d.h. kxk = kyk), so stehen x+y und x−y senkrecht
aufeinander.
kxk2 = kyk2 . Mit (a) folgt dann
hx + y, x − yi = kxk2 − kyk2 = 0. Da das Skalarprodukt Null ist,
Vektoren gleich lang bedeutet
stehen
x+y
und
senkrecht aufeinander.
hx + y, x − yi sowie kxk und kyk für
(i) x = (0; 1; 2) und y = (1; 1; 0)
√
√
√
√
kxk = 02 + 12 + 22 = 5, kyk = 12 + 12 + 02 = 2,
x + y = (1; 2; 2) und x − y = (−1; 0; 1) ⇒ hx + y, x − yi = −1 + 0 + 2 = 1.
sowie
(ii) x = (2; 1; 2) und y = (1; 2; −2)
√
√
√
2
kxk = 2 + 12 + 22 = 9 = 3 = kyk = 12 + 22 + 22 ,
x + y = (3; 3; 0) und x − y = (1; −1; 4) ⇒ hx + y, x − yi = −3 − 3 + 0 = 0.
Fazit: Hier sind x und y gleich lang sowie x + y und x − y aufeinander senkrecht.
(c) Berechnen Sie
x−y
3.
(a) Bestimmen Sie die Norm der Vektoren
y = (−1; 0; 1; 2; −1) ∈ R5 sowie
den Winkel zwischen x und y .
√
√
kxk = 12 + 22 + 32 + 42 + 52 = 55 ≈ 7, 416,
√
√
kyk = 12 + 02 + 12 + 22 + 12 = 7 ≈ 2, 646
und hx, yi = 1 · (−1) + 2 · 0 + 3 · 1 + 4 · 2 + 5 · (−1) = 5.
Für den Winkel α zwischen beiden Vektoren folgt cos α =
x = (1; 2; 3; 4; 5)
und
√5
55·7
≈ 0, 2548 ⇒ α ≈ 75, 2o .
z = (1; −2; 1; 0; 0) auf x und auf y senkrecht steht.
hz, xi = 1 − 4 + 3 + 0 + 0 = 0 = hz, yi = −1 + 0 + 1 + 0 + 0.
(b) Zeigen Sie, dass
Es ist
5.
(a) Geben Sie eine Parameterdarstellung der Geraden
(2; 2)
im
g
R2
durch die Punkte
(3; 0)
und
an.
Mit dem Ortsvektor
v = (2; 2) − (3; 0) = (−1; 2)
und dem Richtungsvektor
x = (3; 0)
erhält man beispielsweise
g=
3
0
+R·
−1
2
=
3
0
−1
2
+t
: t∈R
.
(b) Berechnen Sie den Schnittpunkt und den Schnittwinkel von
g
mit der zweiten Koordina-
tenachse.
Der Schnittpunkt hat die Form
0
x2
=
3
0
+t
−1
2
=
und t. Aus der Gleichung
−t =
fürdie 1.
Komponente
folgt
3
0
x2
man den Schnittpunkt
3
0
=
+3·
−1
2
0
6
=
3−t
2t
.
tung der zweiten Koordinatenachse zeigt. Somit ist der Winkel
cos α =
hv,wi
kvk·kwk
v
=
x2
0 ⇔ t = 3, eingesetzt erhält
Zur Berechnung des Schnittwinkels stellt man fest, dass der Vektor
Richtungsvektor
mit passenden
α
w=
zwischen
0
1
w
in Richund dem
der Geraden zu bestimmen:
√2
5·1
√2
5
=
≈ 0, 89 ⇒ α ≈ 26, 6o ≈ 0, 464
(c) Berechnen Sie den Abstand von
Dazu kann der Ortsvektor
x=
g
rad
zum Koordinatenursprung
3
0
(0; 0).
, der eine Verbindung zwischen dem Ursprung und
der Geraden darstellt,
ineine Parallel- und eine Senkrechtkomponente bezüglich des Rich
tungsvektors
x|| =
hx,vi
hv,vi
−1
2
v=
·v =
−3
v
5
=
zerlegt werden. Man erhält
0, 6
−1, 2
Der gesuchte Abstand ist die
g
h
g
h=
+R·
2
1
=
√6
5
2, 4
1, 2
=
6
5
2
1
≈ 2, 68.
(0; 1)
geht
=
0
1
+t
2
1
x⊥
(sowie alle skalaren Vielfachen
und kann somit als Richtungsvektor von
dienen. Man erhält (z. B.)
0
1
0, 6
−1, 2
steht.
davon) senkrecht auf dem Richtungvektor von
an, die durch den Punkt
Nach Konstruktion steht der in (c) berechnete Vektor
h
x⊥ = x − x|| =
−
2 6 √
6
Norm kx⊥ k = 5 1 = 5· 5=
und
(d) Geben Sie eine Parameterdarstellung der Geraden
und senkrecht auf
3
0
: t∈R
.