Lösungen I.1 a) Punkte, Strecken, Geraden, Längenmaße 1) 2) C

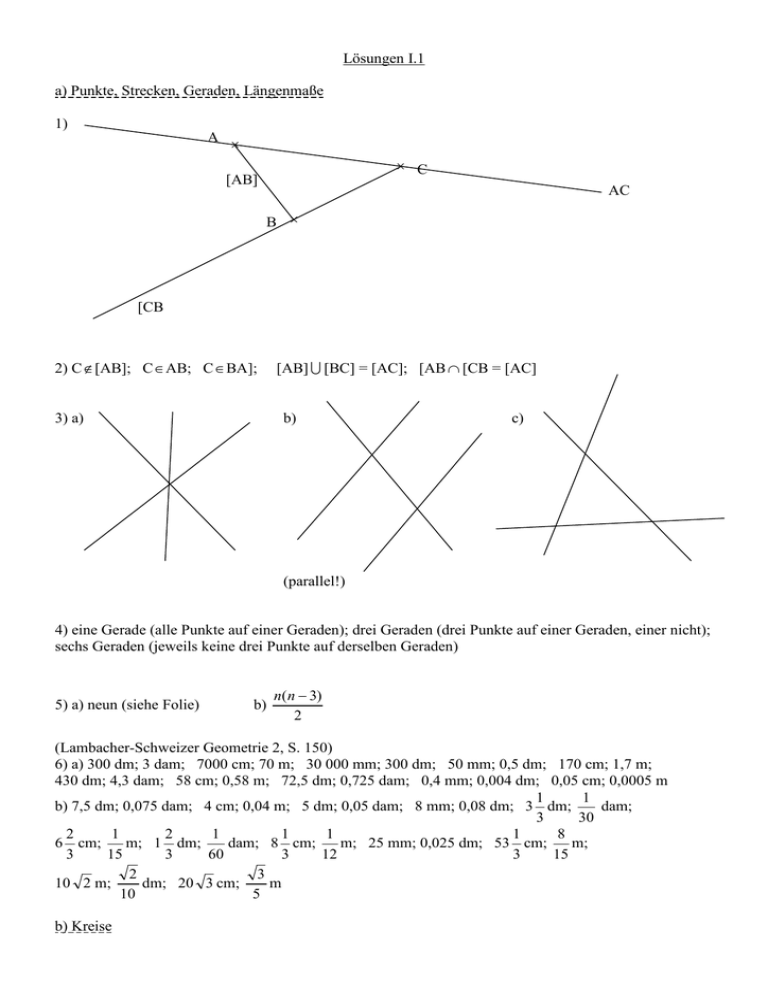
Lösungen I.1
a) Punkte, Strecken, Geraden, Längenmaße
1)
A ×
× C
[AB]
AC
B ×
[CB
2) C∉[AB]; C ∈ AB; C ∈ BA];
3) a)
[AB] U [BC] = [AC]; [AB ∩ [CB = [AC]
b)
c)
(parallel!)
4) eine Gerade (alle Punkte auf einer Geraden); drei Geraden (drei Punkte auf einer Geraden, einer nicht);
sechs Geraden (jeweils keine drei Punkte auf derselben Geraden)
5) a) neun (siehe Folie)
b)
n(n − 3)
2
(Lambacher-Schweizer Geometrie 2, S. 150)
6) a) 300 dm; 3 dam; 7000 cm; 70 m; 30 000 mm; 300 dm; 50 mm; 0,5 dm; 170 cm; 1,7 m;
430 dm; 4,3 dam; 58 cm; 0,58 m; 72,5 dm; 0,725 dam; 0,4 mm; 0,004 dm; 0,05 cm; 0,0005 m
1
1
b) 7,5 dm; 0,075 dam; 4 cm; 0,04 m; 5 dm; 0,05 dam; 8 mm; 0,08 dm; 3 dm;
dam;
3
30
2
1
2
1
1
1
1
8
6 cm;
m; 1 dm;
dam; 8 cm;
m; 25 mm; 0,025 dm; 53 cm;
m;
3
15
3
60
3
12
3
15
2
3
dm; 20 3 cm;
m
10 2 m;
10
5
b) Kreise
6) a) {P | PA ≤ r1} ∩ {P | PB > r2 }
c) {P | r1 < PR ≤ r2 }
8)
b) {P | PA ≤ r1} ∩ {P | PB ≥ r2 }
d) {P | PM 1 > r1} ∩ {P | PM 2 ≤ r2 } ∩ {P | PM 3 ≤ r3 }
Lösungen I.2
12)
13) a) innerhalb eines Kreises um B mit Radius 3 cm
b) außerhalb eines Kreises um A mit Radius 2,5 cm; M’ = {P | AP > 2,5 cm}
Q
Q ∈ M; R∉M
Lösungen I.3
12) (Stark 7 S. 129/14)
13) (Stark 7 S. 129f/16)
a) (1) 1°6’40’’ (2) 1°13’ (3) 9°5’35’’ (4) 1°3’40’’
b) (1) 115,2° (2) 190,42° (3) 11,41° (4) 65,855°
c) (1) 62°30’ (2) 36°21’36’’ (3) 99°9’9’’ (4) 10°33’36’’
d) (1) 371°7’ (2) 45°47’30’’ (3) 1’1’’ (4) 181°2’’
14) (Stark 7 S. 130f/19)
a) 50°
15) (Stark 7 S. 130/18)
b) 360°
b) 75°
c) 99°
d) 12,5°
c) 180°
Lösungen I.4
a) Winkel an Geradenkreuzungen
19) (Stark 7 S. 132/24) α = 49°13’; β = 83°
18) (Stark 7 S. 132/22) 117,35°
20) (Stark 7 S .133/25) α = 80°; β = 30°; γ = 80°; δ = 70°
b) Winkel an Doppelkreuzungen
22) (Stark 7 S. 133/27) δ = 148; ε = 32°
23) (Stark 7 S. 134/29) Stufen- und Wechselwinkel ergänzen sich jeweils zu 180°
24) (Stark 7 S. 134/30) γ = 40°; δ = 140°; ε = 68°
c) Winkelsumme im Dreieck
25) (Stark 7 S. 134/31)
a) 180° – 38° – 52° = 90°
b) 83°
26) (Stark 7 S. 135/32)
a) γ = 138° (Nebenwinkel); δ = 42° (Wechselwinkel); ε = 110° (Scheitelwinkel); α = 70° (Stufenwinkel
zu Nebenwinkel); β = 68° (Winkelsumme im Dreieck)
b)β = 40° (Nebenwinkel); δ = 40° (Stufenwinkel); α = 50° (Winkelsumme im Dreieck); ε = 40°
(Nebenwinkel zu α und 90° bzw. Winkel mit paarweise senkrechten Schenkeln); γ = 130° (Nebenwinkel
zu Stufenwinkel)
d) Winkelsumme im n-Eck
33) (Stark 7 S. 138/40)
b) α = β = γ = 72°; δ = 144°
a) 56,9°
34) (Stark 7 S. 138/41)
gibt es nicht
35) (Stark 7 S. 139/43)
Widerspruch zu Winkelsumme im Dreieck
c) 120°
d) n = 12; µ = 30°
36) (Stark 7 S. 139/44)
a) α = 68° (Nebenwinkel); β = 43° (Stufenwinkel); δ = 69° (Winkelsumme
im Dreieck); γ = 69° (Wechselwinkel)
b) β = 90° − α; γ = α
37) (Stark 7 S. 140/45)
a) α = 50,9° (Stufenwinkel); γ = 45° (Winkelsumme im Dreieck)
c) β = 135° (Nebenwinkel zu Stufenwinkel); bei D
38) (Stark 7 S. 140/46)
Nebenwinkel)
39) (Stark 7 S. 140/47)
40) (Stark 7 S. 141/48)
41) (Stark 7 S. 142/49)
a) g||h
b) 147,1° (Stufenwinkel; Nebenwinkel; Winkelsumme im Dreieck;
α = 30°; δ = 60°; β = 120°; ε = 30°; µ = 150°; γ = 120°
α = 30°; β = 56°; γ = 60°; δ = 124°
a) g||h, weil Stufenwinkel gleich
b) α = 20°; β = 70°; γ = 70°; δ = 70°