Bernoulli-Verteilung √ E[K] = p · 1 + (1 − p) · 0 = p √ Weil die

Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Aufgabe 2
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
Handyklingeln in der Vorlesung
3
(19 Punkte)
19
Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von
p während einer Vorlesung zumindest einmal klingelt.
Sei K eine diskrete Zufallsvariable, die angibt, ob das Handy in der Vorlesung mindestens
einmal klingelt (K = 1) oder nicht (K = 0).
a)* Welcher aus der Vorlesung bekannte Verteilungstyp ist geeignet, um K zu beschreiben?
Bernoulli-Verteilung
1
√
b)* Geben Sie den Erwartungswert von K an.
1
√
E [K ] = p · 1 + (1 − p) · 0 = p
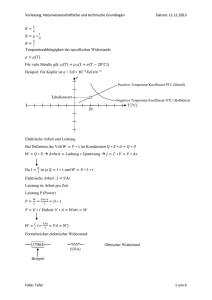
c)* Zeichnen Sie die kumulative Verteilungsfunktion FK (ξ). Achten Sie auf eine korrekte
Beschriftung der Achsen und kennzeichnen Sie bei Unstetigkeitsstellen die Zugehörigkeit
der Randpunkte.
3
FK (ξ)
1
1−p
√
√
1
ξ√
Nun soll eine Zufallsvariable X betrachtet werden, die angibt, wie oft das Handy während
der Vorlesung klingelt.
d)* Warum sind in diesem Modell K und X stochastisch abhängig?
Weil die Realisierung von K durch die Realisierung von X eindeutig fest√
gelegt ist.
Stochastische Signale WS 2010/2011
1
4
X werde beschrieben durch die Zähldichte
pX (k) = e−λ
1
k ∈ N0 .
e)* Wie nennt man diesen Verteilungstyp?
Poisson-Verteilung
2
λk
,
k!
√
f)* Berechnen Sie die Wahrscheinlichkeit P ({X = 0}).
P ({X = 0}) = pX (0)
√
0
= e−λ λ0! = e−λ
√
Damit das Modell sinnvoll ist, muss P ({K = 1}) = P ({X > 0}) gelten.
2
g)* Wie muss hierzu λ für gegebenes p gewählt werden?
!
p = P ({K = 1}) = P ({X > 0}) = 1 − e−λ
√
λ = − ln(1 − p)
1
h)* Geben Sie den Erwartungswert von X in Abhängigkeit von λ an.
E [X ] = λ
1
√
√
i) Geben Sie an, wie sich E [X ] für p → 0 verhält, wenn λ gemäß Aufgabe g) gewählt wird.
p→0
E [X ] = λ = − ln(1 − p) → 0
√
Stochastische Signale WS 2010/2011
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
j) Überprüfen Sie, ob K und X für p < 1 korreliert sind.
Hinweis: Auf Grund der Definition von K und X gilt KX = X .
E [KX ] = E [X ] = λ
√
E [K ] E [X ] = pλ = λ = E [KX ]
√
⇒ korreliert
5
3
√
k)* Berechnen Sie P ({X = 1}|{K = 1}) für den Fall λ = 1 und p = 1 − e−1 .
Hinweise: P ({K = 1}|{X = 1}) = 1, e ≈ 8/3.
P ({K = 1}|{X = 1}) · P ({X = 1}) √
P ({K = 1})
−λ √
1 · λe
e−1
3/8
3√
=
=
≈
=
p
1 − e−1
1 − 3/8 5
P ({X = 1}|{K = 1}) =
Stochastische Signale WS 2010/2011
3
10
10
Aufgabe 3
Tafel im N1190
(10 Punkte)
Angenommen, ein Mitarbeiter der TUM überprüft einmal täglich, ob die Tafel im Hörsaal
N1190 noch funktioniert. Sei D eine diskrete Zufallsvariable, die angibt, nach wie vielen
Tagen der Mitarbeiter eine defekte Tafel vorfindet.
Während der gesamten Aufgabe werde angenommen, dass es keine Unterschiede zwischen
den 7 Wochentagen gibt.
1
a)* Welcher aus der Vorlesung bekannte Verteilungstyp ist geeignet, um die Verteilung von
D möglichst einfach zu beschreiben?
Die geometrische Verteilung.
Nun werde die stetige Zufallsvariable T betrachtet, welche den genauen Zeitpunkt angibt,
an dem die Tafel kaputt geht.
1
b)* Warum sind in diesem Modell D und T stochastisch abhängig?
Weil die Realisierung von D durch die Realisierung von T eindeutig festgelegt ist.
T werde beschrieben durch die Wahrscheinlichkeitsdichtefunktion
fT (t) = λe−λt
2
mit λ =
1
.
210 Tage
c)* Wie nennt man diesen Verteilungstyp und welche besondere Eigenschaft zeichnet ihn
aus?
Es handelt sich um eine Exponentialverteilung. Diese ist gedächtnislos.
Stochastische Signale WS 2010/2011
Name: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Matrikel-Nr.: . . . . . . . . . . . . . . . . . . .
11
d)* Angenommen, zu Beginn des Wintersemesters (t = 0) funktioniere die Tafel.
Bestimmen Sie die Wahrscheinlichkeit des Ereignisses A = {Die Tafel funktioniert am Ende
des Wintersemesters noch}. Nehmen Sie dazu an, dass ein Semester stets 15 Wochen
dauert. Hinweis: √1e ≈ 0.6065.
P (A) = P ({T > 15 · 7 Tage}) =
=
∞
105 Tage
∞
4
fT (t) dt
15·7 Tage
t
− 210 Tage ∞
]105 Tage
λe−λt dt = [−e−λt ]∞
105 Tage = [−e
1
= √ ≈ 60.65%.
e
e) Angenommen, die Tafel geht während des Semesters und der folgenden Semesterferien
nicht kaputt. Wie groß ist dann die Wahrscheinlichkeit, dass sie auch am Ende des
Sommersemesters noch funktioniert? Verwenden Sie die gleiche Semesterlänge wie in
Aufgabe d) und begründen Sie Ihre Antwort. Hinweis: Eine Rechnung ist nicht zwingend
erforderlich.
Sei B = {Die Tafel funktioniert zu Beginn des Sommersemesters} und
C = {Die Tafel funktioniert am Ende des Sommersemesters}. Dann gilt
P (C|B) = P (A) ≈ 60.65%,
weil die Exponentialverteilung gedächtnislos ist.
Stochastische Signale WS 2010/2011
2