so ss D - konrad-ulm

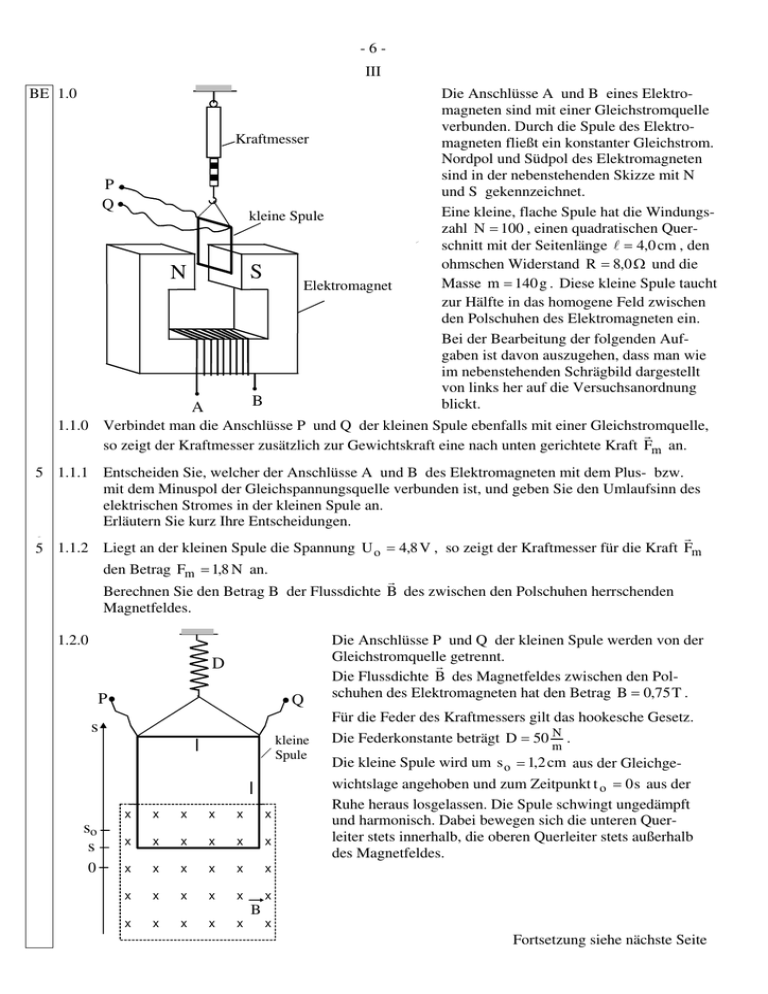
-6III
BE 1.0
Kraftmesser
P
Q
..
kleine Spule
S
N
Elektromagnet
.B
.
A
Die Anschlüsse A und B eines Elektromagneten sind mit einer Gleichstromquelle
verbunden. Durch die Spule des Elektromagneten fließt ein konstanter Gleichstrom.
Nordpol und Südpol des Elektromagneten
sind in der nebenstehenden Skizze mit N
und S gekennzeichnet.
Eine kleine, flache Spule hat die Windungszahl N = 100 , einen quadratischen Querschnitt mit der Seitenlänge l = 4,0 cm , den
ohmschen Widerstand R = 8,0 Ω und die
Masse m = 140 g . Diese kleine Spule taucht
zur Hälfte in das homogene Feld zwischen
den Polschuhen des Elektromagneten ein.
Bei der Bearbeitung der folgenden Aufgaben ist davon auszugehen, dass man wie
im nebenstehenden Schrägbild dargestellt
von links her auf die Versuchsanordnung
blickt.
1.1.0 Verbindet man die Anschlüsse P und Q der kleinen Spule ebenfalls mit einer Gleichstromquelle,
r
so zeigt der Kraftmesser zusätzlich zur Gewichtskraft eine nach unten gerichtete Kraft Fm an.
5 1.1.1 Entscheiden Sie, welcher der Anschlüsse A und B des Elektromagneten mit dem Plus- bzw.
mit dem Minuspol der Gleichspannungsquelle verbunden ist, und geben Sie den Umlaufsinn des
elektrischen Stromes in der kleinen Spule an.
Erläutern Sie kurz Ihre Entscheidungen.
r
5 1.1.2 Liegt an der kleinen Spule die Spannung U o = 4,8 V , so zeigt der Kraftmesser für die Kraft Fm
2,5
den Betrag Fm = 1,8 N an.
r
Berechnen Sie den Betrag B der Flussdichte B des zwischen den Polschuhen herrschenden
Magnetfeldes.
1.2.0
D
.
.
P
Q
s
kleine
Spule
l
l
so
s
0
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
B
Die Anschlüsse P und Q der kleinen Spule werden von der
Gleichstromquelle getrennt.
r
Die Flussdichte B des Magnetfeldes zwischen den Polschuhen des Elektromagneten hat den Betrag B = 0,75 T .
Für die Feder des Kraftmessers gilt das hookesche Gesetz.
Die Federkonstante beträgt D = 50 N .
m
Die kleine Spule wird um s o = 1,2 cm aus der Gleichgewichtslage angehoben und zum Zeitpunkt t o = 0 s aus der
Ruhe heraus losgelassen. Die Spule schwingt ungedämpft
und harmonisch. Dabei bewegen sich die unteren Querleiter stets innerhalb, die oberen Querleiter stets außerhalb
des Magnetfeldes.
x
x
Fortsetzung siehe nächste Seite
-7BE
Fortsetzung III
3 1.2.1 Berechnen Sie die Frequenz f der Schwingung der kleinen Spule.
[ Ergebnis: f = 3,0 Hz ]
6 1.2.2 Bestimmen Sie eine Gleichung mit eingesetzten Werten, die für t ≥ 0 s die Abhängigkeit der
zwischen den Anschlüssen P und Q auftretenden Spannung U von der Zeit t beschreibt.
2.0
Ein Kondensator mit der Kapazität C und ein ohmscher Widerstand R = 100 kΩ sind in Reihe
geschaltet und werden zum Zeitpunkt t o = 0 s durch Schließen eines Schalters an eine Gleichspannungsquelle mit der Spannung U o = 2,00 kV angeschlossen. Der zeitliche Verlauf der Aufladestromstärke I wird experimentell untersucht. Es ergeben sich folgende Ergebnisse:
t in s
2,0
4,0
8,0
12,0
16,0
20,0
I in mA
12,0
7,4
2,7
1,0
0,4
0,1
3 2.1
Zeichnen Sie eine Schaltskizze zu diesem Versuch.
5 2.2
Berechnen Sie die Aufladestromstärke I o für den Zeitpunkt t o = 0 s und zeichnen Sie das
t-I-Diagramm.
Maßstab: 2,0 s =ˆ 1cm ; 2,0 mA =ˆ 1cm
4 2.3
Berechnen Sie die Spannung U C ( t1 ) , die zum Zeitpunkt t1 = 8,0 s am Kondensator anliegt.
[Ergebnis: U C ( t1 ) = 1,73 kV ]
4 2.4
Bis zum Zeitpunkt t1 = 8,0 s fließt auf den Kondensator die Ladung Q( t1 ) .
Kennzeichnen Sie Q( t1 ) im t-I-Diagramm von 2.2 und bestimmen Sie anhand des Diagramms
einen Näherungswert für die Ladung Q( t1 ) .
Hinweis: Es genügt, mit einer graphischen Methode einen Näherungswert für Q( t1 ) zu bestimmen.
[ mögliches Ergebnis: Q( t1 ) = 69 mAs ]
3 2.5
Berechnen Sie die Kapazität C des Kondensators.
3.0
Ein Plattenkondensator mit Luft als Dielektrikum ( ε r , Luft = 1,0 ), dem Plattenabstand
d = 8,0 mm und der Plattenfläche A = 720 cm 2 wird an eine Gleichspannungsquelle mit der
Spannung U o = 2,00 kV angeschlossen und bleibt mit der Spannungsquelle verbunden.
4 3.1
Berechnen Sie die Ladung Q, die auf den Kondensator fließt, und den Energieinhalt Wel des elektrischen Feldes, das zwischen den geladenen Platten des Kondensators herrscht.
3.2.0 Eine Platte aus Kunststoff (Dielektrizitätszahl ε r = 5,4 ) wird innerhalb von 5,0 s zwischen die
Kondensatorplatten gleichmäßig eingeschoben und füllt schließlich den Raum zwischen den
Kondensatorplatten vollständig aus.
4 3.2.1 Erläutern Sie, warum während des Einschiebens der Kunststoffplatte ein Strom fließt.
4 3.2.2 Berechnen Sie die während des Einschiebens der Kunststoffplatte auftretende mittlere
Stromstärke I .
50
-2BE 1.0
.
A
I
.
In vielen Freizeitbädern ist die
Wasserrutsche eine besondere
Attraktion. In einer Rinne rutschen
Badegäste auf einem dünnen Wasserfilm, der die Reibung zwischen dem
Badegast und der Rutschbahn stark
verringert, in ein Wasserbecken.
B
h
. . .
H
C
D
E
Die Bewegung eines Badegastes mit der Masse m = 40 kg auf einer solchen Rutsche soll in den
folgenden Aufgaben untersucht werden. Dabei sind Reibungskräfte zu vernachlässigen.
In der oben stehenden Skizze ist die Bahn, auf der sich der Schwerpunkt des Badegastes zunächst
bewegt, durch eine gestrichelt gezeichnete Linie dargestellt.
3 1.1
Der Badegast stößt sich aus der Ruhe heraus so kräftig ab, dass die Rutschfahrt im Punkt A mit
einer Geschwindigkeit vom Betrag v A = 2,3 m beginnt.
s
Die Abstoßkraft ist horizontal gerichtet. Der Abstoß dauert 0,90 s .
Berechnen Sie den mittleren Betrag der Kraft, mit der sich der Badegast abstößt.
3 1.2
Zwischen den Punkten B und C ist die Rutschbahn um den Winkel α = 35 o gegen die
Horizontale geneigt.
r
Berechnen Sie den Betrag a der Beschleunigung a , die der Badegast bei der Bewegung
von B nach C erfährt.
4 1.3
Die Höhe der Rutsche beträgt h = 5,6 m . Den Punkt D passiert der Badegast mit der
r
Geschwindigkeit v D .
r
Berechnen Sie den Betrag v D der Geschwindigkeit v D .
1.4.0
Q
4 1.4.1
6 1.4.2
6 1.5
Im Punkt E mündet die Rutsche in eine horizontal
liegende Kurve. Der Schwerpunkt des Badegastes
bewegt sich nun mit einer Geschwindigkeit vom
Betrag v = 11 m auf einem Kreisbogen mit dem
s
Radius r = 10 m . Dabei schließt die Körperachse
r
mit der Vertikalen den Winkel ϕ ein.
Die nebenstehende Skizze zeigt einen Querschnitt
Rutschrinne
durch die Rutschrinne und den Badegast.
Erstellen Sie einen Kräfteplan, der alle auf den Badegast wirkenden Kräfte und deren Resultierende enthält.
r
Berechnen Sie den Winkel ϕ und den Betrag der Kraft FN , die der Badegast auf die Rutschrinne ausübt.
Der Badegast verlässt im Punkt F die
Rutsche
F
Rutschbahn mit einer horizontal
r
gerichteten Geschwindigkeit v F vom
.
Wasseroberfläche
50 cm
s
Beckenrand
Betrag v F = 11 m . In der Entfernung s
s
vom Beckenrand trifft er mit der
r
Geschwindigkeit v W auf der 50 cm
tiefer liegenden Wasseroberfläche auf.
r
Berechnen Sie die Entfernung s und den Winkel β , den die Auftreffgeschwindigkeit v W mit
der Wasseroberfläche einschließt.
Fortsetzung siehe nächste Seite
BE
-3Fortsetzung I
2.0
Nach dem bohrschen Atommodell für das Wasserstoffatom kann das Elektron den Atomkern, der
aus einem Proton besteht, nur auf bestimmten Kreisbahnen umlaufen.
Für den Radius rn einer solchen Kreisbahn gilt: rn = r1 ⋅ n 2 mit n ∈♦ und r1 = 5,3 ⋅ 10 − 11 m .
Im Grundzustand des Wasserstoffatoms ( n = 1 ) bewegt sich das Elektron auf der Kreisbahn mit
dem kleinsten Radius r1 = 5,3 ⋅ 10 − 11 m .
Gravitationskräfte werden im bohrschen Atommodell vernachlässigt.
3 2.1
Das Elektron befindet sich auf der Kreisbahn mit dem Radius r1 = 5,3 ⋅ 10 − 11 m . Das Elektron und
der Atomkern tragen ungleichnamige Ladungen; dennoch fällt das Elektron nicht in den Kern.
Erläutern Sie diesen Sachverhalt.
4 2.2
Berechnen Sie den Betrag v1 der Geschwindigkeit, mit der das Elektron den Atomkern auf der
Kreisbahn mit dem Radius r1 umläuft.
5 2.3
Bewegt sich das Elektron auf einer Kreisbahn mit dem Radius rn ( rn = r1 ⋅ n 2 ), so besitzt es die
kinetische Energie E kin , n .
Zeigen Sie, dass gilt: E kin , n = 2,2 ⋅ 10 − 18 J ⋅ 12
n
2.4.0
.
ϕ(r ) sei das elektrische Potenzial, das der Atomkern des Wasserstoffatoms in der Entfernung r
vom Atomkern erzeugt.
Das elektrische Potenzial in unendlich großer Entfernung vom Atomkern sei gleich null.
2 2.4.1 Erläutern Sie, was man unter einer Äquipotenzialfläche versteht.
2 2.4.2 Zeigen Sie, dass für das elektrische Potenzial ϕ n , das der Atomkern auf der Kreisbahn mit dem
Radius rn erzeugt, gilt: ϕ n = 27 V ⋅ 12 .
n
2.5.0 Die potenzielle Energie des Elektrons im elektrischen Feld des Atomkerns sei in unendlich
großer Entfernung vom Atomkern gleich null.
4 2.5.1 Berechnen Sie die Gesamtenergie E ges,1 eines Elektrons, das sich auf der Kreisbahn mit dem
Radius r1 befindet.
4 2.5.2 Dem Elektron auf der Kreisbahn mit dem kleinsten Radius r1 muss eine Mindestenergie zugeführt werden, damit es den Anziehungsbereich des Atomkerns verlassen kann. Man bezeichnet
diese Mindestenergie als Ionisierungsenergie.
Bestimmen Sie mit Hilfe eines Energieansatzes die Ionisierungsenergie E ion für das Wasserstoffatom.
50
BE
1.0
-4II
Für kleine Auslenkwinkel schwingt ein Fadenpendel harmonisch. In einem Messversuch soll
der Zusammenhang zwischen der Periodendauer T der Pendelschwingung, der Masse m des
Pendelkörpers und der Pendellänge l untersucht werden. Bei der Durchführung des Versuchs
erhält man folgende Messergebnisse:
Messung Nr.
1
m in g
50
120
l in cm
T in s
2,20
2
50
35
1,19
3
50
15
0,78
4
50
55
1,50
5
25
55
1,49
6
75
55
1,51
7
100
55
1,50
3 1.1
Nennen Sie die Nummern derjenigen Messungen, in denen der Zusammenhang zwischen
T und m untersucht wird.
Geben Sie an, ob und gegebenenfalls wie die Periodendauer T der Pendelschwingung von der
Masse m des Pendelkörpers abhängt. Begründen Sie Ihre Antwort anhand der Messwerte.
5 1.2
Bestätigen Sie durch graphische Auswertung der Messreihe, dass gilt: T = k ⋅
wobei k konstant, d.h. unabhängig von l ist.
l ,
1.3.0 Das Fadenpendel aus der Messung Nr. 4 mit der Pendellänge l = 55 cm wird um den Winkel
α = 10 o aus der Ruhelage ausgelenkt. Zum Zeitpunkt t o = 0 s wird der Pendelkörper mit der
Masse m = 50 g aus der Ruhe heraus losgelassen. Das Pendel schwingt dann harmonisch mit
der Periodendauer T = 1,50 s .
5 1.3.1 Berechnen Sie die Amplitude A der harmonischen Schwingung und bestimmen Sie eine
Gleichung mit eingesetzten Werten, welche die Abhängigkeit der Elongation s des Pendelkörpers von der Zeit t für t ≥ 0 s beschreibt.
[ Teilergebnis: A = 9,6 cm ]
3 1.3.2 Berechnen Sie den Betrag v R derjenigen Geschwindigkeiten, mit denen sich der Pendelkörper
durch die Ruhelage bewegt.
[ Ergebnis: v R = 0,40 m ]
s
r
4 1.3.3 Beim Durchgang durch die Ruhelage übt der Faden auf den Pendelkörper die Kraft FF aus.
r
Berechnen Sie den Betrag FF der Fadenkraft FF .
5 1.3.4 Berechnen Sie diejenigen Elongationen s1 und s 2 , bei denen die kinetische Energie des
Pendelkörpers 75% der gesamten Schwingungsenergie beträgt.
1.4.0 L 1
Nr. 1
Hebel
L2
Querstange
Nr. 2
Nr. 3
In der skizzierten Anordnung sind an einer drehbaren Querstange die Fadenpendel aus den
Messungen mit den Nummern 1, 2 und 3
angebracht.
Am linken Ende der Querstange ist ein Hebel
befestigt. Bewegt man den Hebel um kleine Auslenkwinkel periodisch hin und her, so wird die
Querstange in den Lagern L1 und L 2 um kleine Winkel hin und her gedreht. Dadurch werden
die Pendel zu Schwingungen angeregt.
Die Dämpfung der Pendelschwingungen ist gering, aber nicht vernachlässigbar.
Die Frequenz f e , mit der die Querstange hin und her gedreht wird, wird stufenweise gesteigert.
Wird f e auf einen neuen Wert eingestellt, so schwingen die Pendel nach einer Einschwingphase
harmonisch.
Fortsetzung siehe nächste Seite
-5BE
Fortsetzung II
3 1.4.1 Wird f e auf den Wert f e,2 = 0,84 Hz eingestellt, so erreichen die Auslenkwinkel des Pendels
aus Messung Nr. 2 maximale Werte.
Geben Sie eine kurze Begründung für diesen Sachverhalt.
4 1.4.2 Vergleichen Sie für die Frequenz f e = f e,2 = 0,84 Hz die Phasenlagen der Schwingungen der
Pendel Nr. 1 und Nr. 3 mit der Phasenlage der Schwingung des Pendels Nr. 2 .
Begründen Sie Ihre Antwort.
2.0
Aus einer Ionenquelle treten zweifach positiv geladene Heliumionen mit vernachlässigbar
kleiner Anfangsgeschwindigkeit aus. Ein Helium-
II
I
B
*
Ionenquelle
r
U
4 2.1
Detektor
ion besitzt die Masse m = 6,64 ⋅ 10 − 27 kg und
trägt die Ladung q = 3,204 ⋅ 10 − 19 C .
Im Bereich I durchlaufen die Ionen die
Beschleunigungsspannung U, die zunächst
auf den Wert U1 = 1,20 kV eingestellt ist.
Im Bereich II wird die Bewegung der Ionen
durch ein Magnetfeld beeinflusst. Das Magnetr
feld ist homogen, seine Flussdichte B ist zeitlich
konstant und hat den Betrag B = 80 mT .
Beim Eintritt in den Bereich II ist die Geschwindigkeit der Ionen senkrecht zu den magnetischen
Feldlinien gerichtet.
Die gesamte Anordnung befindet sich im Vakuum. Der Einfluss der Gravitationskraft auf die
Bewegung der Ionen kann vernachlässigt werden.
r
Ein Ion verlässt den Bereich I mit der Geschwindigkeit v1 .
r
2⋅q ⋅ U1
.
Zeigen Sie, dass für den Betrag v1 der Geschwindigkeit v1 gilt: v1 =
m
Berechnen Sie v1 für ein Heliumion.
r
2.2.0 Die Ionen dringen mit der Geschwindigkeit v1 in den Bereich II ein, bewegen sich auf einem
Viertelkreis mit dem Radius r und gelangen schließlich in einen Detektor.
r
3 2.2.1 Geben Sie die Richtung von B an, und begründen Sie, dass bei der Bewegung im Bereich II
der Betrag der Bahngeschwindigkeit eines Ions konstant bleibt.
4 2.2.2 Zeigen Sie, dass zwischen B, U1 , m, q und r der folgende Zusammenhang gilt:
m=
q⋅B 2 2
⋅r .
2 ⋅ U1
3 2.2.3 Berechnen Sie den Radius r des Viertelkreises, auf dem sich die Heliumionen bewegen.
[ Ergebnis: r = 8,8 cm ]
2.3
Die Helium-Ionenquelle wird durch eine Ionenquelle ersetzt, aus der ebenfalls zweifach positiv
geladene Ionen mit vernachlässigbar kleiner Anfangsgeschwindigkeit austreten. Die Masse m*
eines solchen Ions ist aber unbekannt.
r
Die magnetische Flussdichte B im Bereich II und die Position des Detektors werden nicht
verändert. Die Spannung U wird so eingestellt, dass der neue Ionenstrahl ebenfalls in den
Detektor gelangt. Dies ist der Fall für U 2 = 0,53 kV .
4
50
Berechnen Sie m* und geben Sie an, um welche Art von Ionen es sich handeln könnte (Angabe
des zugehörigen chemischen Elements).