Anorganisch-Chemisches Fortgeschrittenen Praktikum Philipps

Bericht zum Vertiefungsprojekt
Anorganisch-Chemisches Fortgeschrittenen
Praktikum
Philipps-Universität Marburg
Kristallstrukturbestimmung
Karsten Müller
Betreuer: Prof. Dr. W. Massa
30.04.2007 - 08.06.2007
1
Inhaltsverzeichnis
1
Einführung
2
Theorie
2.1 Kristallgitter . . . . . . . . . . .
2.1.1 Das Translationsgitter .
2.1.2 Die 14 Bravais-Gitter . .
2.2 Geometrie der Röntgenbeugung
2.3 Das reziproke Gitter . . . . . . .
2.4 Der Reflex und seine Intensität .
2.4.1 Atomfaktoren . . . . . .
2.4.2 Temperaturfaktoren . . .
2.4.3 Strukturfaktoren . . . .
2.5 Bestimmung der Kristallstruktur
2.5.1 Strukturlösung . . . . .
2.5.2 Strukturverfeinerung . .
2.5.3 Hindernisse und Fallen .
2.5.4 Verwendete Programme
3
Röntgenstrukturen
3.1 RbCr . . . . . .
3.2 NEtAl . . . . .
3.3 SD3a . . . . .
3.4 SD1a . . . . .
3.5 Mue . . . . . .
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
5
6
10
13
15
15
15
16
16
18
20
21
22
.
.
.
.
.
23
23
29
35
39
45
1
Einführung
Kristallstrukturanalyse ist die Bestimmung des atomaren Aufbaus eines Kristalls
durch Beugung geeigneter Strahlung am Kristallgitter. Da die interatomaren Abstände im Bereich von ca. 100 - 300 pm (1-3 Å) mit lichtmikroskopischen Untersuchungen nicht zugänglich sind (vgl. Abbildung 1), wird hierfür sehr häufig
monochromatische Röntgenstrahlung verwendet, da sich diese verhältnismäßig
einfach als charakteristische Röntgenstrahlung in einer Röntgenröhre erzeugen
lässt. Für diese Analysemethode hat sich der Begriff Röntgenstrukturanalyse eingebürgert.
Abbildung 1: Wellenlängen elektromagnetischer Strahlung [1]
Alternativ lassen sich auch Neutronenstrahlen oder Synchrotronstrahlung verwenden. Die Kristallstrukturanalyse mit Elektronenstrahlen ist aufgrund der starken Wechselwirkung zwischen den eingestrahlten Elektronen und dem Kristall
besonders schwierig und für Routineuntersuchungen noch nicht ausgereift.
1912 erkannte Max von Laue das durch den dreidimensionalen gitterartigen
Aufbau von Kristallen durch Bestrahlung Interferenz zu ertwarten ist. Wird Strahlung ohne Änderung der Wellenlänge am Kristallgitter durch Interferenz zu vielen
in verschiedenen Raumrichtungen beobachtbaren Reflexen abgelenkt, spricht man
von Röntgenbeugung. Aus dem beobachteten Beugungsmuster kann anschließend
die Kristallstruktur berechnet werden. Die Geometrie der Elementarzelle des Kristallgitters kann vollständig anhand der Winkel abgeleitet werden, unter denen die
Beugungsmaxima auftreten. Aus der Stärke der Beugungsmaxima wird mittels
3
verschiedener mathematischer Methoden die Anordnung der Atome innerhalb der
Elementarzelle berechnet. Die hierbei benötigten Rechnungen werden allerdings
bereits für mittelgrosse Moleküle (ab etwa 10 Nicht-Wasserstoffatomen) so komplex, dass sie ohne Computer nicht mehr durchführbar sind.
Auf dem Gebiet der Kristallstrukturanalyse gab es mehrere Nobelpreise, angefangen bei Max von Laue und Wilhelm Conrad Röntgen, die die Grundlagen
legten, über Dorothy Crowfoot Hodgkin, die viele biologisch relevante Moleküle erstmalig strukturell bestimmte, bis zu Robert Huber und Johann Deisenhofer,
die Proteine (unter anderem auch das chlorophyllhaltige Photoreaktionszentrum
in Pflanzen) als Proteinkristalle untersuchten. Eines der bekanntesten Beispiele
für die Strukturaufklärung mittels Röntgenbeugung ist die Entschlüsselung der
DNA-Struktur durch James Watson und Francis Crick, deren Modell wesentlich
auf Röntgenbeugungsdaten von Maurice Wilkins und Rosalind Franklin beruhte.
1985 wurde Jerome Karle und Herbert A. Hauptman der Nobelpreis für Chemie
für deren Beiträge zur Entwicklung der "Direkten Methoden" zur Kristallstrukturanalyse zuerkannt.
Die Kristallstrukturanalyse ist ein gutes Beispiel für den zunehmenden Vernetzungsgrad der wissenschaftlichen Disziplinen. Sie zeigt das nur durch Einbeziehung verschiedenster wissenschaftlicher Erkenntnisse Methoden und Wissen
gewonnen werden.
4
2
2.1
2.1.1
Theorie
Kristallgitter
Das Translationsgitter
Die Struktur von Kristallen wird duch die Begriffe Gitter und Basis beschrieben.
Abbildung 2: Gitter und Basis in der Kristallstruktur [1]
Das Kristallgitter, oder Punktgitter, ist eine dreidimensionale Anordnung von
Punkten. Die kleinste Einheit ist die Elementarzelle. Sie enthält alle Informationen, die zur Beschreibung des Kristalls notwendig sind. Die Elementarzelle wird
durch Translationsymmetrie zu einem dreidimensionalen Netz erweitert, welches
den (idealen) Kristall darstellt. Sie ist ein Hilfsmittel, um die Symmetrie und Geometrie des Kristalls zu beschreiben.
Die Basis einer Kristallstruktur sind Atome, Ionen oder Moleküle. Sie werden
im Kristall angeordnet und bestehen mindestens aus einer Atomsorte, können aber
auch tausende Atome umfassen (Proteinkristalle).
Beim Kochsalz besteht die Basis aus einem Na+ - und einem Cl − -Ion.
Die Literatur spricht in diesem Zusammenhang von Gitterstrukturen. Es wird daher in Analogie zu bekannten Strukturen vom Natriumchloridgitter, Cäsiumchloridgitter, usw. gesprochen.
5
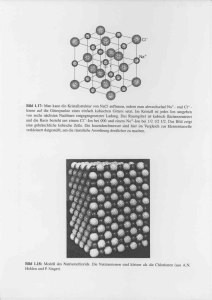
Abbildung 3: NaCl-Kristallstruktur [1]
2.1.2
Die 14 Bravais-Gitter
Zur Beschreibung der Symmetrie und Geometrie eines Kristalls dient das Kristallgitter als Hilfsmittel. Im dreidimensionalen Raum beschreiben die Bravais-Gitter
(nach Auguste Bravais) oder auch Raumgitter jede mögliche Zellenform. Sie stellen die Menge aller im dreidimensionalen Raum möglichen Elementarzellen der
Kristalle da. Sie besitzen folgende Eigenschaften:
1. Die Elementarzelle ist die einfachste sich wiederholende Einheit in einem
Kristall.
2. Gegenüberstehende Flächen sind parallel.
3. Der Rand der Elementarzelle verbindet äquivalente Stellen.
Ein Bravais-Gitter besteht nur aus einer Teilchensorte. So ergibt sich z.B. für das
NaCl-Gitter durch Translation je ein kubisch-flächenzentriertes Gitter aus Na+ und Cl − -Ionen.
6
Abbildung 4: NaCl-Kristallstruktur [6]
Die vorangegangene Definition liefert insgesamt 14 Bravais-Gitter. Sie sind
im Folgenden in abnehmender Symmetrie aufgelistet:
primitiv
raumzentriert
flächenzentriert
Abbildung 5: kubisches Kristallsystem [1]
7
primitiv
raumzentriert
Abbildung 6: tetragonales Kristallsystem [1]
primitiv
basiszentriert
raumzentriert
Abbildung 7: rhombisches Kristallsystem [1]
8
primitiv
Abbildung 8: hexagonales Kristallsystem [1]
primitiv
basiszentriert
Abbildung 9: monoklines Kristallsystem [1]
9
primitiv
Abbildung 10: triklines Kristallsystem [1]
Stellt man die Beziehungen der Basisvektoren a, b und c und die Winkel α, β
und γ jeden Gittertyps gegenüber, ergibt sich folgende
Tabelle zu den Bravais-Typen:
Kristallsystem
Restriktion der Gitterkonstanten
kubisch
a=b=c
tetragonal
a=b
rhombisch
keine
hexagonal, trigonal a = b
monoklin
keine
triklin
keine
Restriktion der Winkel
α = β = γ = 90
α = β = γ = 90
α = β = γ = 90
α = β = 90γ = 120
α = γ = 90γ 6= 90
α 6= β 6= γ 6= 90
Tabelle 1: Bravais-Gitter nach Kristallsystemen geordnet
2.2
Geometrie der Röntgenbeugung
Wie bereits in der Einführung erwähnt, kommt es bei der Bestrahlung eines Kristallgitters mit Röntgenstrahlung zu Interferenzerscheinungen. Das Auftreten von
Interferenz hängt vom Einstrahlwinkel θ , der Wellenlänge der Strahlung λ und
dem Abstand der Gitter d untereinander ab.
10
Entscheidend für das Auftreten von Interferenzerscheinungen ist der Gangunterschied. Der Gangunterschied δ (vgl. Abbildung 11) ist die Wegdifferenz zweier
oder mehrerer Wellen gleicher Wellenlänge.
Abbildung 11: schematische Darstellung des Gangunterschiedes [1]
Beträgt der Gangunterschied zweier Wellen bei gleicher Wellenlänge und Amplitude genau eine halbe Wellenlänge (plus einem beliebigen ganzzahligen Vielfachen der Wellenlänge), löschen sich die beiden Teilwellen aus. Man nennt diese
Intensitätsschwächung destruktive Interferenz. Beträgt er ein ganzzahliges Vielfaches der Wellenlänge, addieren sich die Amplituden der beiden Teilwellen. In
diesem Fall liegt konstruktive Interferenz vor. Bei Werten dazwischen ergibt sich
eine teilweise Auslöschung.
Dieser Zusammenhang wurde von William Henry Bragg und seinem Sohn
William Lawrence Bragg in der Bragg-Gleichung formuliert.
nλ = 2d sin θ
(1)
Durch die Bragg-Gleichung wird der Abstand d zwischen den parallelen Ebenen
im Kristallgitter mit der Wellenlänge λ der Röntgenstrahlung und dem Winkel θ
zwischen Röntgenstrahl und Ebene miteinander verknüpft. n ist hierbei ein natürliche Zahl und stellt die Beugungsordnung dar.
Ist sie erfüllt, kommt es zu konstruktiver Interferenz der bei der Beugung an
den Elektronenhüllen entstehenden Kugelwellen, so dass die Röntgenstrahlung
von einem Photodetektor oder einem Film aufgenommen werden kann (vgl. Abbildung 12 auf der nächsten Seite). Makroskopisch entsteht so der Eindruck einer
Reflexion am Kristall.
11
Jede Schar paralleler Gitterebenen hat einen charakteristischen Gitterebenenabstand d und damit, so die Bragg-Gleichung, auch einen charakteristischen Braggwinkel θ . Eine Reflexion (kurz: ein Reflex) kann nur dann beobachtet werden,
wenn eine Schar paralleler Gitterebenen (genannt: Netzebenen) so orientiert ist,
dass der Röntgenstrahl genau unter dem Braggwinkel θ einfällt.
Die Orientierung dieser Netzebenen im Translationsgitter wird mit den MillerIndizes genannten Werten h, k und l beschrieben. Die hkl-Indices einer Ebene
werden ermittelt, indem die Ebene die dem Nullpunkt am nächsten liegt herausgegriffen wird. Sie schneidet die a−, b− und c−Achse der Elementarzelle in den
Achsenabschnitten 1/h, 1/k und 1/l. Die Kehrwerte sind die Indices hkl, die somit die Ebene kennzeichnen. Ein Index 0 beschreibt also einen Achsenabschnitt
im Unendlichen, also eine parallel verlaufende Ebene.
Für verschiedene Winkel, unter denen Röntgenstrahlung auf den Kristall trifft,
erhält man auf der Fotoplatte hinter dem Kristall fast immer auch verschiedene Bilder, weil sich immer andere Scharen paralleler Gitterebenen (mit anderen Braggwinkeln und mit anderen Orientierungen im Kristall) in Reflexionsstellung zum einfallenden Röntgenstrahl befinden. Die Bragg-Gleichung erlaubt so
durch Interpretation des Beugungsbildes, aus dem sich der Bragg-Winkel errechnen lässt, die Berechnung des Netzebenenabstandes und damit auch die Berechnung der Ausmaße der Elementarzelle.
Abbildung 12: schematische Darstellung der Beugung [1]
12
2.3
Das reziproke Gitter
Ist die Elementarzelle eines Kristalls bekannt, können also alle möglichen Netzebenen (hkl) konstruiert werden. Somit können über ihre Netzebenenabstände
d die Beugungswinkel der zugehörigen Reflexe hkl berechnet werden. Da für die
Strukturaufklärung viele Netzebenen gleichzeitig dargestellt werden müssen, wird
es schnell sehr unübersichtlich. Abhilfe schafft hier die vektorielle Darstellung jeder Netzebenenschar. Hierbei wird jede Schar durch den Vektor d beschrieben,
welcher die Richtung der Flächennormalen und die Länge des Netzebenenabstandes hat. Somit stellt jeder Reflex auf dem Detektor einen Punkt (den Endpunkt
des d-Vektors) in der Elementarzelle dar. Wegen des reziproken Zusammenhanges | d |∼ 1/sinθ werden diese d-Vektoren jedoch umso kürzer, je höher die hklIndices (bzw. die Beugunswinkel) werden. Alle d-Vektoren enden deshalb in der
Elementarzelle.
Da die Achsenabschnitte a/h, b/k und c/l ebenfalls reziprok mit den MillerIndices hkl zusammenhängen, läßt sich durch einführen der reziproken Einheiten
a∗ , b∗ und c∗ statt der realen Größen a, b und c eine Vereinfachung erreichen.
a∗ , b∗ und c∗ sind definiert als:
b×c ∗ a×c ∗ a×b
,b =
,c =
(2)
V
V
V
Es gilt allgemein, dass die reziproke Achse senkrecht auf der realen Achse
∗ spannen das reziproke Gitter auf. Jeder darin enthalsteht. Die Streuvektoren dhkl
tene Punkt mit den Koordinaten hkl entspricht einem Reflex.
a∗ =
2
2
2
2
d ∗ = h2 a∗ + k2 b∗ + l 2 c∗
(3)
Durch die Einführung der Ewald-Konstruktion (nach Paul Peter Ewald) wird
klar, das das reziproke Gitter zur praktischen Durchführung von Beugungsexperimenten geeignet ist. Mit ihrer Hilfe läßt sich die Laue-Bedingung für konstruktive
Interferenz darstellen.
13
Abbildung 13: Ewald Konstruktion [1]
Man zeichnet die Punkte des reziproken Gitters des Kristalls auf (in Abbildung
13 ist ein zweidimensionaler Schnitt gezeigt). In dieses Netz wird nun der Wel→
−
lenzahlvektor k der einfallenden Welle so eingezeichnet, dass er am Gitterpunkt
→
−
(000) endet. Der Anfangspunkt von k sei A. Dieser fällt i.A. nicht mit einem Gitterpunkt zusammen. Um A wird nun eine Kugel (in der Abbildung ein Kreis) mit
→
−
→
−
→
−
dem Radius | k | eingezeichnet. Bei der elastischen Streuung gilt | k |=| k0 |(d.h.
dass sich bei der Streuung nur die Richtung des einfallenden Strahls ändert, nicht
jedoch der Betrag des Wellenvektors).
Das bedeutet nun, dass alle Wellenvektoren der gebeugten Wellen von A ausgehend ebenfalls auf der Kugeloberfläche enden. Notwendige Voraussetzung für
das Auftreten eines Beugungsmaximums ist aber nun, dass die Laue-Bedingung
− →
→
− →
− →
−
∆ k = k0 − k = G
(4)
→
−
erfüllt ist. Dies ist genau für die abgebeugten Wellenvektoren k0 der Fall, die von
A ausgehend auf Punkte des reziproken Gitters zeigen (also die Gitterpunkte die
von der Oberfläche der Ewald-Kugel geschnitten werden). In der Abbildung ist
14
→
−
→
−
dies für zwei Wellenvektoren ( k10 mit zugehörigem reziproken Gittervektor G 1
→
−
−
→
sowie k0 2 mit zugehörigem reziproken Gittervektor G2 ) illustriert.
2.4
Der Reflex und seine Intensität
Da die gemessenen Reflexe nicht alle die gleich Intensität haben, muss die BraggBedingung (vgl. Gleichung 1 auf Seite 11) noch duch weitere Faktoren beeinflusst
werden. Im Folgenden werden die drei Faktoren mit dem höchsten Anteil an der
Reflexintensität aufgeführt.
2.4.1
Atomfaktoren
Da die Streuung der Röntgenstrahlung an der Elektronenhülle der Atome erfolgt,
ist die Amplitude des gestreuten Welle proportional zur Elektronenzahl, also der
Ordnungszahl des Elements. Desweiteren nimmt die Streuamplitude aufgrund von
Phasenverschiebungen mit zunehmendem Beugungswinkel θ ab. Die Winkelabhängigkeit variiert durch die Elektronendichteverteilung der verschiedenen Atome. Daher wird diese winkelabhängige atomare Streuamplitude als Atomformfaktor f bezeichnet.
2.4.2
Temperaturfaktoren
Aufgrund von Schwingungen der Atom um ihre Nullpunktlage erfahren die Atomformfaktoren eine Schwächung. Diese Schwingung kann gleichmäßig in alle Richtungen (isotrop) oder in manche Reichtungen bevorzugt (anisotrop) erfolgen. Als
Temperaturfaktor wird das Quadrat der mittleren Schwingungsamplitude bezeichnet. Für anisotrope Schwingungen ergibt sich analog ein Ellipsoid (vgl. Abbildung
14).
15
Abbildung 14: Ellipsoid mit (a, b, c) = (4, 2, 1) [1]
2.4.3
Strukturfaktoren
Die bei der Beugung an einer Netzebene entstehende Streuwelle erleidet eine Phasenverschiebung bezogen auf eine vom Nullpunkt ausgehende Welle. Die Phasenverschiebung läßt sich als komplexe Zahl dastellen. Für eine Reflex hkl überlagern
sich die Streuwellen aller Atome i auf den jeweiligen Positionen xi , yi , zi in der
Elementarzelle unter Berücksichtigung der Phasenverschiebung. Die Kugelwelle
die für die gesamte Struktur resultiert bezeichnet mal als Strukturfaktor. Er wird
nach Gleichung 5 berechnet:
Fc = ∑ fi {cos 2π(hxi + kyi + lzi } + i sin 2π(hxi + kyi + lzi )}
(5)
i
2.5
Bestimmung der Kristallstruktur
Zu Beginn einer jeden Bestimmung steht der Kristall. In unserem Projekt lagen zu
jedem Messungauftrag bereits Kristalle vor. Auf den mitunter sehr aufwendigen
Bereich der Einkristallzüchtung wird daher an dieser Stelle nicht weiter eingegangen.
Um einen möglichst idealen Kristall in die Messung einzubringen, wird unter
einem Lichtmikroskop ein Kristall passender Größe (0.1 - 0.5 mm) ausgewählt.
Durch Polarisationsfilter kann die Polarisation des Lichtes eingestellt werden. So
16
kann der Kristall mit polarisiertem Licht durchstrahlt werden. Stehen die Filter um
90° verdreht zueinander verdunkelt sich der Kristall. Verwachsungen oder andere
Unordnungen in der Kristallstuktur werden durch helle Bereich sichtbar. Es gilt
einen möglichst gleichmäßigen Kristall zu finden, da er nach der Messung, die
Stunden bis Tage dauert, den besten Messdatensatz liefert.
Ist ein geeigneter Kristall gefunden, wird er auf einer Kunststoffschleife (vgl.
Abbildung 15) mit Öl fixiert und auf dem Goniometerkopf montiert.
Abbildung 15: Cryoschleife mit Kristall in Öl [14]
Der Goniometerkopf wird so eingerichtet, dass der Kristall sich im Strahlengang befindet und bei Rotation sich der Schwerpunkt nicht oder nur sehr wenig
ändert. Es folgt eine orientierende Messung. Es werden wenige Aufnahmen auf
dem Flächendetektorsystem (weisser Schirm links in Abbildung 16) gemacht und
aus ihnen die Elementarzelle und deren Orientierungsmatrix bestimmt. Die daraus
erhaltenen Werte lassen eine Optimierung der Messparameter (Detektordistanz,
Winkeländerung, Belichtungszeit des Detektors) zu. Mit den optimierten Messparametern wird die eigentliche Messung gestartet. Eine vollständige Aufnahme
kann bis zu mehreren Tagen dauern.
17
Abbildung 16: Flächendetektorsystem Stoe IPDS mit Tieftemperatureinrichtung
[15]
Den Beginn der Auswertung stellt die Integration über alle gemessene Reflexe
dar. Der PC kann aus den Integralen die Netzebenen im reziproken Raum grafisch
darstellen. Durch spezielle Auslöschungen kann auf eine vorliegende Symmetrie
geschlossen werden. Mit der Laue-Gruppe ist die Bestimmung der Raumgruppe
möglich.
Um eine Strukturlösung zu beginnen, ist noch eine Vermessung des Kristallformats am Diffraktometer nötig.
2.5.1
Strukturlösung
Zur Strukturlösung wird die erhaltene dreidimensionale periodische Elektronendichtefunktion ρ per Fouriertransformation in ihre Einzelwellen zerlegt. Die Einzelwellen entsprechen den Strukturfaktoren mit ihrer Phasenverschiebung. Durch
18
Fouriersynthese kann die Elektronendichtefunktion zurückberechnet werden.
ρ=
1
V
∑ Fhkl e−i2π(hx+ky+lz)
(6)
hkl
Da durch die Integration der Reflexe allerdings nur die Beträge ermittelt werden, ist vom Fourierkoeffizient F0 nur dessen Betrag bekannt. Die Phaseninformation geht durch Integration verloren. Dieser Verlust wird als das Phasenproblem der Kristallstrukturanalyse bezeichnet. Das Problem wird in der Strukturlösung durch unterschiedliche Methoden gelöst. Allen gemein ist, das sie mit einem Strukturmodell arbeiten und für den folgenden Lösungsweg eine DifferenzFouriersynthese verwenden.
Folgende Methoden finden Anwendung:
• Patterson-Methode:
Nach Arthur Lindo Patterson benannte Methode. Die Patterson-Methode ist als
die Fouriertransformierte der Beträge der Strukturfaktorquadrate definiert.
P(U,V,W ) =
∞
∞
1 ∞
| F(hkl) |2 ·e[−2πi(hU+kV +lW )]
∑
∑
∑
VEZ h=−∞ k=−∞ l=−∞
(7)
Lindo Patterson selbst nannte sein Verfahren deshalb die |F 2 | -Reihe. Sie liefert dabei nicht direkt die Positionen der Atome in der Elementarzelle, sondern
interatomare Vektoren. Die Länge des Vektors ist der interatomare Abstand, die
Richtung die interatomare Richtung. Die Höhe des Peaks ist abhängig von der
Elektronenzahl der beiden beteiligten Atome. Je größer die Elektronenzahl ist, desto höher ist der Peak. In der Kristallstrukturanalyse wird die Patterson-Methode
deshalb bevorzugt eingesetzt, wenn die Kristallstruktur aus wenigen Schweratomen und vielen Leichtatomen besteht. Die höchsten Peaks geben dann die interatomaren Vektoren zwischen den Schweratomen an. Ist die Lage der Schweratome
bestimmt, kann ihr partieller Strukturfaktor ermittelt und vom errechneten Strukturfaktor abgezogen werden. Auf diese Weise kann die Lage der übrigen Atome
bestimmt werden. Da sich die Intensität aus dem Produkt der Elektronenzahlen
errechnet, versagt die Patterson-Methode jedoch bei Anwesenheit vieler ähnlich
schwerer Atome.
19
• direkte Methode
Die Entwicklung der direkten Methode geht auf Harker und Kasper zurück. 1948
erkannten sie den Zusammenhang zwischen Intensität und Phase. Sie schafften somit eine direkte Methode zur Lösung des Phasenproblems. Beginnend mit einem
Anfangssatz an Reflexen mit bekannter Phase wird durch verschiedene Beziehungen unter Einbeziehung normierter Strukturfaktoren oder E-Werte ein Satz neuer
Phasen berechnet. Die Sayre-Gleichung liefert aus der Summe von Produkten der
Strukturfaktoren aller Reflexpaare den Strukturfaktor eines Reflexes hkl.
Fhkl = k ·
Fh0 k0 l 0 · Fh−h0 ,k−k0 ,l−l 0
∑
0 0 0
(8)
hkl
Durch die von Karle und Hauptmann eingeführte mathematische Auswertung
dieser Beziehung, hat sich dieses Prinzip in der Praxis ebenfalls durchgesetzt. Für
diese Methode wurde Jerome Karle und Herbert A. Hauptmann 1985 der Nobelpreis für Chemie verliehen.
Liegen viele Atome (> 200) in der Elementarzelle vor, stößt die direkte Methode jedoch an ihre Grenze.
2.5.2
Strukturverfeinerung
Wurde durch eine der genannten Methoden ein Strukturmodell erhalten ist eine Verfeinerung notwendig, da die erhaltenen Elektronendichtemaxima mitunter
stark fehlerbehaftet sind. Durch Verfeinerung werden diese Fehler minimiert und
als Resultat ein Optimum ermittelt, welches die geringsten Fehlerquadrate aufweist.
Die Methode der kleinsten Fehlerquadrate zur Strukturverfeinerung sucht ein
Minimum für die Summe der Fehlerquadrate gemittelt über alle Messungen.
∑ w(FO2 − FC2) = Min.
(9)
Dazu wird über die Differenz zwischen berechneten (C wie calculated) und
gemessenen (O wie observed) Fehlerquadraten summiert. Die Summe beinhaltet einen Gewichtungsfaktor w, welcher Unterschiede der Reflexe im Datensatz
20
berücksichtigt.
Die Verfeinerung kann anhand der F0 -Daten (Gleichung 10) oder der F02 Daten (Gleichung 11) erfolgen.
R=
∑hkl || FO | − | Fc ||
∑hkl | FO |
s
wR2 =
∑hkl (FO2 − Fc2 )2
∑hkl (FO2 )2
(10)
(11)
Die daraus erhaltene Reststandardabweichung R wird als konventioneller RWert bzw. gewichteter R-Wert (wR2 ) bezeichnet. Sie sind ein Maß für die Richtigkeit der Strukturlösung. Je kleiner ihre Beträge, desto exakter ist die Übereinstimmung des Modells mit den Messwerten.
Sind die R-Werte hinreichend gut und wurde in der Verfeinerung die Absorption, Extinktion und Anisotropie berücksichtigt, werden enthaltene Wasserstoffatome in den Strukturvorschlag übernommen.
Da Wasserstoffatome naturgemäß eine sehr geringe Elektronendichteverteilung und somit auch nur ein sehr geringes Streuvermögen besitzen, können sie
durch eine Differenzfouriersynthese nur bei einem guten Messdatensatz lokalisiert werden. Ist der Datensatz unzureichend für eine freie Verfeinerung der Wasserstoffatome, so werden sie unter Berücksichtigung der Bindungsgeometrie hinzugerechnet. Hierbei können die bindenden Atome wahlweise als starr (AFIX)
betrachtet werden oder ihre Bindungsvektoren werden bei der Verfeinerung mitverschoben, falls sich der Ort des Bindungspartners nach einer Verfeinerung ändert.
Nach einer abschließenden Einbeziehung von Auslenkungsparametern für isotrope Schwingungen und Berücksichtung anisotroper Auslenkungsellipsoide werden geometrische Daten der Struktur berechnet. Auf ihrer Grundlage ist eine grafische Darstellung der Struktur möglich.
2.5.3
Hindernisse und Fallen
Die vorangegange Herleitung einer Struktulösung ist stark idealisiert. Es gibt bei
jedem Schritt von der Messung bis zur Verfeinerung eine Vielzahl von Hindernis21
sen und Stolperfallen, die es zu berücksichtigen gilt. Eine Beschreibung besagter
Hindernisse würde den Rahmen dieses Berichts sprengen, ich verweise daher auf
einschlägige Literatur [2, 3, 4] und erwähne nur ein paar in folgender Auflistung.
• Verzwilligungen innerhalb des Kristalls
• Fehlordnung innerhalb des Kristalls
• Quasikristallinität
• falsche Bestimmung der Raumgruppe
• anormale Dispersion
• λ /2-Effekt
• Konformationsänderungen (temperaturabhängig)
• thermisch diffuse Streuung
2.5.4
Verwendete Programme
Die Entwicklung elektronischer Datenverarbeitung hat auch in der Kristallstrukturanalyse Einzug gehalten und eine Vielzahl an Arbeitsschritten stark vereinfacht. Während noch vor wenigen Jahren die Auswertung von photografischen
Filmen per Bleistift und Taschenrechner zum Alltag des Kristallographen gehörte, ist heute die Aufnahme und Auswertung der Messergebnisse weitestgehend
automatisiert. Dieser Umstand sollte jedoch nicht darüberhinweg täuschen, dass
immer noch ein detailiertes Verständnis der Programme und ihrer Arbeitsweise
nötig ist. Ein out-of-the-box-System welches sämtliche Hindernisse umschifft und
zielsicher in kürzester Zeit mit geringstmöglicher Reststandardabweichung per
Knopfdruck einen Strukturvorschlag liefert ist - wenn überhaupt - Zukunftsmusik. Dennoch sind heutige Programme sehr leistungsfähig und sollten an dieser
Stelle keinesfalls unerwähnt bleiben.
Für die Strukturlösung und -verfeinerung wurde das Programmpaket SHELX97 [12] von G. M. Sheldrick verwendet. Es besteht aus dem Programm SHELXS
[8] zur Strukturlösung und SHELXL [9] zur Verfeinerung.
22
Besagte Programme sind in die Programm-Suite WinGX [10, 11] (An Integrated System of Windows Programs for the solution, refinement and analysis of
single crystal x-ray diffraction data) in der Version 1.70.01 eingebettet, welche
eine Vielzahl weiterer Programme zur Verfügung stellt.
Zur Strukturlösung wurde im Fall von SD3a das Programm SIR-2004 eingesetzt [13].
3
3.1
Röntgenstrukturen
RbCr
Ein tiefroter Kristall der Rubidium-Chrom-Verbindung wurde im STOE-Diffraktometer
mit einem IPDS-Flächendetektorsystem bei 193 K vermessen.
Die vorgeschlagene Summenformel lautete C6 H11CrNO5 Rb.
Bei der Bestimmung der Elementarzelle ergab sich ein triklines Kristallsystem
vom aP-Bravaistyp. Somit fällt eine ungeordnete Raumgruppe ohne Symmetrie
P1 und eine innenzentrierte symmetrische Raumgruppe P1 in Betracht. Da für die
Winkel der Elementarzelle α 6= β 6= γ gilt, ergibt sich mit 1 als Punktgruppe P1
als korrekte Raumgruppe.
In den E-Statistics des Programms WinGX32 wurde ebenfalls die Raumgruppe
P1 bevorzugt.
Gelöst wurde die Struktur mit dem Programm SHELXS-97 [8] mit Hilfe der
Patterson-Methode (aufgrund der Schwermetallionen) bis zu einem konventionellen R-Wert von 0.0398 (wR2 = 0.0962) und einem GooF (Goodness of Fit) von
0.960 (vgl. Tabelle 2). Eine Suche nach der Summenformel und den Gitterkonstanten im Cambridge Crystallographic Data Centre (CCDC) lieferte keine Ergebnisse.
Weitere Daten des Kristalls sind in Tabelle 2 zusammengefasst.
23
Tabelle 2: Kristall- und Messdaten RbCr
Kristalldaten
Farbe, Habitus
klar, dunkelrot
Summenformel
C17 H17CrN2 O14 Rb2
molare Masse
636,22 g/mol
Abmessungen
0.50 x 0.20 x 0.14 m3
Dichte (berechnet)
2.083 g/cm3
Kristallsystem
triklin
Raumgruppe
P1
Zellvolumen
507.19(11)Å3
Z
2
Elektronenzahl / F(000)
313
Absoptionskoeffizient µ
5,407 mm−1
Messparameter
Diffraktometer / Detektor
STOE mit IDPS
Strahlung
Mo - Kα (0.71073 Å)
Temperatur
193 K
Detektorabstand
50 mm
gemessene Reflexe
8958
davon symmetrieunabhängig
2353 (Rin =0.0627)
Daten / Restraints / Parameter
2353 / 3 /124
θ -Bereich
2.82 - 30.27° (90.4 %)
2
Goodness-of-Fit per F
0,960
R-Werte (I>2σ (I))
R1 = 0.0398, wR2 = 0.0933
R-Werte (alle Daten)
R1 = 0.0498, wR2 = 0.0962
Restelektronendichte max./min. +0.71 e− ·Å−3 , -1.43 e− ·Å−3
Gitterkonstanten:
a=6.4559(8) Å
α=106.779(14)°
b=8.4095(10) Å
β =95.831(15)°
c=9.8175(13) Å
γ=90.694(14)°
Der anfängliche Ansatz, über den Rb-Rb und Rb-Cr-Abstand durch Vektoraddition den Chromvektor im Raum festzulegen, lieferte eine sehr große Reststandardabweichung. Nach Festlegung des Chroms als Ursprung der Elementarzelle
und nochmaligem Lösen der Struktur mit SHELXS-97 verbesserten sich die R1 Werte. Anschließend wurde die Verfeinerung mit dem Programm SHELXL-97
[9] durchgeführt werden. Bei der Verfeinerung wurden eine Absorptionskorrektur
(Gaussian), Anisotropie und eine Extinktionskorrektur berücksichtigt.
24
Nach einer ersten Strukturlösung konnte ein Fragment nicht eindeutig geklärt
werden, darum betrachteten wir die Elektronendichteverteilung des Fragments mit
dem Programm XP in WinGX32 [10] (vgl. Abbildung 17). Das Fragment bestand
aus vier nahezu planar angeordneten Atomen (Torsionswinkel 178,78°). Die Bindungslängen zwischen dem zentralen Atom und den äußeren Atomen betragen
1,25 bzw. 1,45 Å. Die Elektronendichteverteilung deutet hier auf eine Halbbesetzung mit Nitrat und Hydrogencarbonat hin (vgl. Abbildung 18 auf der nächsten
Seite). Dies erklärt auch die einzelne längere Bindung. In der abschließenden Verfeinerung wurden Wasserstoffbrücken berücksichtigt.
Abbildung 17: Elektronendichteverteilung C7/N7-Fragment
25
Abbildung 18: C7/N7 - Fragment
In der Struktur ist ein Chromatom verzerrt oktaedrisch von vier Sauerstoffen
und zwei Stickstoffen des EDTA umgeben (vgl. Abbildung 19 auf der nächsten
Seite). Die Bindungslängen zwischen dem Chromatom und den Sauerstoffatomen O12, O1, O3 und O13 betragen 1.96 Å, die zu den Stickstoffatomen N1 und
N2 2.08 Å. Durch dir Chrom-Stickstoff-Bindungen ergiben somit den gestreckten
Oktaeder. Das Rubidium hingegen liegt zwischen acht Sauerstoffatomen (fünf aus
EDTA, zwei aus Carbonat/Nitrat und eins aus der Alkoholfunktion) koordiniert
vor (vgl. Abbildung 20 auf der nächsten Seite). Eine Auswahl an Bindungslängen
findet sich in Tabelle 3.
In den Abbildungen 21, 22 und 23 wird die Chromlage auf den Ecken der
triklinen Zelle deutlich. Die primitive, zentrosymmetrische Einheitszelle ist ebenfalls gut erkennbar.
26
Abbildung 19: oktaedrisch koordiniertes Chrom in RbCr
Abbildung 20: 8-fach koordiniertes Rubidium in RbCr
27
Abbildung 21: RbCr - Blick entlang der a-Achse
Abbildung 22: RbCr - Blick entlang der b-Achse
28
Abbildung 23: RbCr - Blick entlang der c-Achse
Atom-Atom
Rb2-O1
Rb2-O2
Rb2-O3
Rb2-O4
Rb2-O5
Rb2-O6
Rb2-O7
Rb2-O8
Bindungslänge in Å
2.901(2)
2.935(2)
2.935(2)
2.9581(18)
2.984(3)
2.998(6)
3.092(2)
3.134(6)
Atom-Atom
CR1-N1
CR1-N2
CR1-O1
CR1-O3
CR1-O12
CR1-O13
Bindungslänge in Å
2.085(2)
2.085(2)
1.9546(19)
1.961(2)
1.9546(19)
1.961(2)
Tabelle 3: ausgewählte Bindungslängen in RbCr
3.2
NEtAl
Bei NEtAl handelte es sich um farblose Kristalle mit der vorgeschlagenen Strukturformel NEt4 [Al EDTA] (Summenformel: C18 H32 AlN3 O8 ). Das Aufstellen der
Elementarzelle ergab erneut ein triklines Kristallsystem. Die Struktur wurde mit
SHELXS97 über die direkte Methode gelöst. Vor der Verfeinerung ergab sich bereits ein R1 -Wert von ca. 0.015.
29
Bei der Verfeinerung stellte sich heraus, dass weder Aluminium noch Tetraethylammonium vorhanden sind, sondern lediglich Kalium-EDTA-Dihydrat K + EDTA− ∗
2 H2 0.
Eine Suche nach der Summenformel und den Gitterkonstanten im Cambridge
Crystallographic Data Centre (CCDC) lieferte keine Ergebnisse. Lediglich das
Monohydrat ist in der Datenbank erfasst.
Bei der Verfeinerung wurden Absorption (Gaussian) und Wasserstoffbrücken
berücksichtigt. Die Wasserstoffe wurden angerechnet, eine Extinktionskorrektur
war nicht notwendig. Kristall- und Meßdaten zu NEtAl sind in Tabelle 4 aufgeführt.
30
Tabelle 4: Kristall- und Messdaten NEtAl
Kristalldaten
Farbe, Habitus
farblos, klar
+
Summenformel
C10 H18 N2 O2−
10 2 K
molare Masse
202.23 g/mol
Abmessungen
0.50 x 0.26 x 0.16 mm3
Dichte (berechnet)
1.703 g/mm3
Kristallsystem
Triklin
Raumgruppe
P1
Zellvolumen
788.65(12) Å3
Z
2
Elektronenzahl / F(000)
420
Absoptionskoeffizient µ
0.657 mm−1
Messparameter
Diffraktometer / Detektor
STOE mit IDPS
Strahlung
Mo - Kα (0.71073 Å)
Temperatur
193 K
Detektorabstand
40 mm
gemessene Reflexe
11709
davon symmetrieunabhängig 4285
Daten / Restraints / Parameter 4285 / 0 / 241
θ -Bereich
3.00 bis 30.30 ° (90.9 %)
2
Goodness-of-Fit per F
0.903
R-Werte (I>2σ (I))
R1 = 0.0263, wR2 = 0.060
R-Werte (alle Daten)
R1 = 0.0381,wR2 = 0.0616
Gitterkonstanten:
a=7.0189(6) Å
α=82.843(10)°
b=9.0290(8) Å
β =85.861(10)°
c=13.3884(12) Å
γ=69.594(9)°
In der erhaltenen Struktur ist Kalium (K1) verzerrt oktaedrisch von 6 Sauerstoffatomen koordiniert (vgl. Abbildung 24 auf der nächsten Seite). Es handelt sich dabei um 5 Sauerstoffatome aus Acetatgruppen und ein Wassermolekül
(O10). Die Kaliumionen bilden eine Schichtstruktur in der jede zweite Lücke mit
einem Wassermolekül besetzt ist (vgl. Abbildung 26). Ausgewählte Bindungslängen sind in Tabelle 5 aufgeführt.
31
Abbildung 24: NEtAl - verzerrt oktaedrisches Kalium
Abbildung 25: NEtAl - Blick entlang der a-Achse
32
Abbildung 26: Kalium EDTA ∗ 2 H2 0- Blick entlang der b-Achse
33
Abbildung 27: NEtAl - Blick entlang der c-Achse
Abbildung 28: Kaliumschichtstruktur in NEtAl
34
Atom-Atom
K1-O4
K1-O11
K1-O10
K1-O2
Bindungslänge in Å
2.7887(10)
2.9094(12)
2.7582(12)
2.8199(10)
Tabelle 5: Ausgewählte Bindungslängen in NEtAl
Bei der 1969 publizierten Struktur von M. Cortrait [7] handelt es sich um
+
C10 H14 N2 O2−
8 2K - Monohydrat. In ihr liegt das Kalium - EDTA in der Raumgruppe P 21 /n vor. Es ist also eine Schraubenachse in einem primitiven Gitter
enthalten. Rechtwinkling zu ihr findest sich eine Gleitspiegelebene mit Translation entlang einer halben Flächendiagonalen. Das primitive Gitter ergibt eine
monokline Zelle mit β = 93, 90 und einem Zellvolumen von 1602, 382 3 . NEtAl
bzw. das K EDTA ∗ 2 H2 0 liegt in einer triklinen Zelle bei einem Zellvolumen von
788,65(12) 3 vor. Es ist der Raumgruppe P1 zugeordnet und weist daher lediglich
eine Innenzentrierung in einem primitiven Gitter auf.
3.3
SD3a
Die Struktur des goldgelben Kristalls SD3a mit der Summenformel
[Cu(C9 H10 N2 )(PPh3 )2 ][BPh4 ] wurde wie folgt geklärt.
Es ergab sich eine monokline zentrosymmetrisch Einheitszelle. Als Raumgruppe wurde C 2/c bestimmt. Im Kristall liegt somit eine Gleitspiegelebene und
senkrecht dazu eine zweizählige Drehachse vor. Eine Strukturlösung mit SHELXS97 brachte kein akzeptables Ergebnis (R1 > 20 %). Eine Verzwilligung wurde
durch prüfen der Einheitszelle ausgeschlossen. Die Struktur wurde durch SIR2004 erhalten. Anschließend konnte mit SHELXL-97 unter Berücksichtigung von
Anisotropie und einer Absorptionskorrektur die vollständige Struktur inklusive aller H-Atome frei verfeinert werden. Eine Extinktionskorrektur und das Auslassen
2
stark fehlerbehafteter Reflexe ( 4F
esd ) waren nicht notwendig. Eine Suche nach der
Summenformel und den Gitterkonstanten im Cambridge Crystallographic Data
Centre (CCDC) lieferte keine Ergebnisse.
35
Die Kristall- und Messdaten sind in Tabelle 6 aufgelistet.
Tabelle 6: Kristall- und Messdaten SD3a
Kristalldaten
Farbe, Habitus
klar, goldgelb
Summenformel
C69 H60 N2 P2
molare Masse
1053.48 g/mol
Abmessungen
0.50 x 0.26 x 0.20 mm3
Dichte (berechnet)
1.260 g/cm3
Kristallsystem
Monoklin
Raumgruppe
C2/c
Zellvolumen
11109.0(16)Å3
Z
8
Elektronenzahl / F(000)
4416
Absoptionskoeffizient µ
0.500 mm−1
Messparameter
Diffraktometer / Detektor
STOE mit IDPS
Strahlung
Mo - Kα (0.71073 Å)
Temperatur
193(2) K
Detektorabstand
45 mm
gemessene Reflexe
47628
davon symmetrieunabhängig 10624 (Rin =0.1201)
Daten / Restraints / Parameter 10624 / 0 / 857
θ -Bereich
2.24 - 25.88° (98.6 %)
2
Goodness-of-Fit per F
0.767
R-Werte (I>2σ (I))
R1 =0.0471, wR2 =0.0871
R-Werte (alle Daten)
R1 = 0.1017, wR1 = 0.0966
Gitterkonstanten:
a= 35.306(3)Å
α=90°
b= 17.2780(15)Å
β =92.885(9)°
c= 18.2340(14)Å
γ=90°
36
Abbildung 29: Struktur SD3a
In SD3a ist das Kupferkation tetraedrisch durch zwei Stickstoffe aus dem
C9 H10 N2 und zwei Phosphoratome aus PPh3 koordiniert (vgl. Abbildung 29) .
Die Raumgruppe C2/c zeigt, das es sich bei SD3a um eine C-zentrierte Zelle mit
einer C2 -Achse handelt. Senkrecht dazu findet sich eine Gleitspiegelebene entlang
der c-Achse.
Die Gleitspiegelebene ist an den Kupfer- und Phosphoratomen in Abbildung
30, die C2 -Achse in Abbildung 31 erkennbar. Ausgewählte Bindungslängen zu
SD3a finden sich in Tabelle 7.
37
Abbildung 30: SD3a - Blick entlang der a-Achse
Abbildung 31: SD3a - Blick entlang der b-Achse
38
Abbildung 32: SD3a - Blick entlang der c-Achse
Atom-Atom Bindungslänge in Å
Cu-N
2.09 - 2.10
Cu-P
2.25
B-C
1.63 - 1.65
Tabelle 7: Ausgewählte Bindungslängen in SD3a
3.4
SD1a
Eine bereits vorhandene Messung des Kristalls SD1a konnte in der Vergangenheit nicht vollständig aufgeklärt werden. Unsere Messung wurde bei eine tieferen Temperatur (100 K) als die Vorherige durchgeführt um Atomschwingungen
stärker zu reduzieren. Die Strukturbestimmung ergab eine monokline Zelle mit
folgenden Gitterkonstanten:
39
Tabelle 8: Kristall- und Messdaten SD1a
Kristalldaten
Farbe, Habitus
klar, goldgelb
Summenformel
C50 H56 N4 B
molare Masse
831.67g/mol
Abmessungen
0.50 x 0.26 x 0.16 mm3
Dichte (berechnet)
1.274g/cm3
Kristallsystem
Monoklin
Raumgruppe
P21 /c
Zellvolumen
4201.0Å3
Z
4
Elektronenzahl / F(000)
1696
Absoptionskoeffizient µ
0.516 mm−1
Messparameter
Diffraktometer / Detektor
STOE mit IDPS
Strahlung
Mo - Kα (0.71073 Å)
Temperatur
193(2) K
Detektorabstand
50 mm
gemessene Reflexe
32425 (99.1 %)
davon symmetrieunabhängig 11489 (Rint =0.0409)
Daten / Restraints / Parameter 11489 / 0 / 729
θ -Bereich
1.95 - 29.40°
2
Goodness-of-Fit per F
1.046
R-Werte (I>2σ (I))
R1 = 0.0465, wR2 =0.1078
R-Werte (alle Daten)
R1 = 0.0519, wR1 = 0.1105
Gitterkonstanten:
a= 13.210Å
α=90°
b=15.215Å
β =105.46°
c= 21.686Å
γ=90°
Durch die niedrigere Temperatur konnte die Struktur aufgeklärt werden. Der
Cycloheptanring im Ligand liegt am C48 und C52 in 2 Konformationen vor (vgl.
C52 und C54 in Abbildung 33). Die unterschiedlichen Konformationen beeinflussen somit die Lage des Silberions. Bei höheren Temperaturen ist es möglich,
das ein Ringflip am Cycloheptanring die Messwerte so stark beeinflusst, das die
Auswertung uneindeutig wird.
Die Raumgruppe P21 /c erzeugt im Kristall ein primitives Gitter mit Innenzentrierung. Es findet sich eine 21 -Schraubenachse und rechtwinklig dazu eine
40
Gleitspiegelebene entlang der c-Achse. Eine Suche nach der Summenformel und
den Gitterkonstanten im Cambridge Crystallographic Data Centre (CCDC) lieferte keine Ergebnisse.
Abbildung 33: Konformationen des Cycloheptanringes
In Abbildung 34 ist an den Silberatomen die 21 -Schraubenachse sehr gut zu erkennen. Die Gleitspiegelebene entlang der c-Achse ist ein Abbildung 34 ebenfalls
gut zu erkennen. Ausgewählte Bindungslängen zu SD1a finden sich in Tabelle 9.
41
Abbildung 34: SD1a- Blick entlang der a-Achse
42
Abbildung 35: SD1a- Blick entlang der b-Achse
43
Abbildung 36: SD1a- Blick entlang der c-Achse
Atom-Atom
Ag A - N (aklyl.)
Ag B - N (alkyl.)
Ag A - N (arom..)
Ag B - N (arom.)
Ag A - C54 A
Ag B - C54 B
C54 A - C54 B
Bindungslänge in
2.34(5)
2.04(2)
2.27(1)
2.45(1)
3.44(1)
3.65(2)
0.89(8)
Tabelle 9: Ausgewählte Bindungslängen in SD1a
44
3.5
Mue
Den Abschluß des Vertiefungsprojektes bildete eine individuelle Strukturaufklärung. Die erhaltenen Messdaten (hkl- und crs-Datei) wurden ohne weitere Informationen über Struktur, Summenformel oder enthaltene Symmetrieelemente ausgewertet. Zu Beginn wurde durch WinGX eine zentrosymmetrische, monokline
Struktur festgestellt. Als Raumgruppe wurde P 21 /n ermittelt. Es ist also, wie bereits im NEtAl, eine Schraubenachse in einem primitiven Gitter enthalten. Rechtwinkling zu ihr findet sich eine Gleitspiegelebene mit Translation entlang einer
halben Flächendiagonalen.
Bei der Betrachtung der Reflexe zeigt sich kein schnelles Abklingen der Reflexintensitäten, was als Hinweis auf Schweratome gedeutet werden kann.
Zur Strukturlösung wurde daher die Patterson-Methode der direkten Methode vorgezogen. Eine Absorptionskorrektur verbesserte den R-Wert gering. Die
Berücksichtigung von Extinktion und eine semi-empirische Absorptionskorrektur
zeigte keine Verbesserung. Eine Suche nach der Summenformel und den Gitterkonstanten im Cambridge Crystallographic Data Centre (CCDC) lieferte keine
Ergebnisse.
45
Tabelle 10: Kristall- und Messdaten Mue
Kristalldaten
Farbe, Habitus
unbekannt
Summenformel
C44 H24 N12 Mn
molare Masse
775.69 g/mol
Abmessungen
unbekannt
Dichte (berechnet)
1.426 g/cm3
Kristallsystem
Monoklin
Raumgruppe
P21 /n
Zellvolumen
unbekannt
Z
4
Elektronenzahl / F(000)
1588
Absoptionskoeffizient µ
0.418 mm−1
Messparameter
Diffraktometer / Detektor
STOE mit IDPS
Strahlung
Mo - Kα (0.71073 Å)
Temperatur
193(2) K
Detektorabstand
unbekannt
gemessene Reflexe
34823 (99.0 %)
davon symmetrieunabhängig 9731 (Rint =0.0448)
Daten / Restraints / Parameter 9731 / 0 / 514
θ -Bereich
1.75 - 29.25 °
2
Goodness-of-Fit per F
0.778
R-Werte (I>2σ (I))
R1 =0.0306, wR2 =0.0597
R-Werte (alle Daten)
R1 = 0.057, wR1 = 0.0644
Gitterkonstanten:
a= 9.6318(5)Å
α=90°
b=30.6516(14)Å
β =90.683(5)°
c= 12.5952(8)Å
γ=90°
In der Einheitszelle befinden sich 4 Formeleinheiten je Elementarzelle. Im
Kristallgitter ist Mangan oktaedrisch durch zwei Phenantrolinliganden (vgl. Abbildungen 38 auf der nächsten Seiteund 37 auf der nächsten Seite) koordiniert.
Die Oktaederwinkel weichen auf 82.9° bis 94.6° aus. Die N - Mn - N -Winkel
sind mit 175 - 176° etwas kleiner als im idealen Oktaeder. Der Blick entlang der
a-Achse zeigt die 21 -Schraubenachse.
46
Abbildung 37: Struktur Mue
Abbildung 38: Phenantrolin
47
Die monokline Elementarzelle mit Blickrichtung entlang der Achsen zeigen
die Abbildungen 39, 40 und 41.
Abbildung 39: Mue - Blickrichtung entlang der a-Achse
48
Abbildung 40: Mue - Blickrichtung entlang der b-Achse
49
Abbildung 41: Mue - Blickrichtung entlang der c-Achse
Atom-Atom Bindungslänge in
Mn - N
1.97(8)
C-N
1.32 - 1.37
C-C
1.32 - 1.44
Tabelle 11: Ausgewählte Bindungslängen in Mue
50
Abbildungsverzeichnis
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Wellenlängen elektromagnetischer Strahlung [1] . . . . . . . . . .
Gitter und Basis in der Kristallstruktur [1] . . . . . . . . . . . . .
NaCl-Kristallstruktur [1] . . . . . . . . . . . . . . . . . . . . . .
NaCl-Kristallstruktur [6] . . . . . . . . . . . . . . . . . . . . . .
kubisches Kristallsystem [1] . . . . . . . . . . . . . . . . . . . .
tetragonales Kristallsystem [1] . . . . . . . . . . . . . . . . . . .
rhombisches Kristallsystem [1] . . . . . . . . . . . . . . . . . . .
hexagonales Kristallsystem [1] . . . . . . . . . . . . . . . . . . .
monoklines Kristallsystem [1] . . . . . . . . . . . . . . . . . . .
triklines Kristallsystem [1] . . . . . . . . . . . . . . . . . . . . .
schematische Darstellung des Gangunterschiedes [1] . . . . . . .
schematische Darstellung der Beugung [1] . . . . . . . . . . . . .
Ewald Konstruktion [1] . . . . . . . . . . . . . . . . . . . . . . .
Ellipsoid mit (a, b, c) = (4, 2, 1) [1] . . . . . . . . . . . . . . . . .
Cryoschleife mit Kristall in Öl [14] . . . . . . . . . . . . . . . . .
Flächendetektorsystem Stoe IPDS mit Tieftemperatureinrichtung
[15] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Elektronendichteverteilung C7/N7-Fragment . . . . . . . . . . . .
C7/N7 - Fragment . . . . . . . . . . . . . . . . . . . . . . . . . .
oktaedrisch koordiniertes Chrom in RbCr . . . . . . . . . . . . .
8-fach koordiniertes Rubidium in RbCr . . . . . . . . . . . . . .
RbCr - Blick entlang der a-Achse . . . . . . . . . . . . . . . . . .
RbCr - Blick entlang der b-Achse . . . . . . . . . . . . . . . . .
RbCr - Blick entlang der c-Achse . . . . . . . . . . . . . . . . . .
NEtAl - verzerrt oktaedrisches Kalium . . . . . . . . . . . . . .
NEtAl - Blick entlang der a-Achse . . . . . . . . . . . . . . . . .
Kalium EDTA ∗ 2 H2 0- Blick entlang der b-Achse . . . . . . . .
NEtAl - Blick entlang der c-Achse . . . . . . . . . . . . . . . . .
Kaliumschichtstruktur in NEtAl . . . . . . . . . . . . . . . . . .
Struktur SD3a . . . . . . . . . . . . . . . . . . . . . . . . . . . .
SD3a - Blick entlang der a-Achse . . . . . . . . . . . . . . . . .
51
3
5
6
7
7
8
8
9
9
10
11
12
14
16
17
18
25
26
27
27
28
28
29
32
32
33
34
34
37
38
31
32
33
34
35
36
37
38
39
40
41
SD3a - Blick entlang der b-Achse . . . .
SD3a - Blick entlang der c-Achse . . . .
Konformationen des Cycloheptanringes .
SD1a- Blick entlang der a-Achse . . . . .
SD1a- Blick entlang der b-Achse . . . . .
SD1a- Blick entlang der c-Achse . . . . .
Struktur Mue . . . . . . . . . . . . . . .
Phenantrolin . . . . . . . . . . . . . . . .
Mue - Blickrichtung entlang der a-Achse .
Mue - Blickrichtung entlang der b-Achse
Mue - Blickrichtung entlang der c-Achse .
52
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
38
39
41
42
43
44
47
47
48
49
50
Literatur
[1] http://de.wikipedia.org 09.06.2007 12:00 Uhr.
[2] W. Massa, Kristallstrukturbestimmung, 2. Auflage, Teubner-Verlag Stuttgart, 1996.
[3] S. Haussühl, Kristallstrukturbestimmung, Wiley-VCH, 1998.
[4] C. Giacovazzo, Fundamentals of Crystallography, 2. Auflage, Oxford University Press, 2002.
[5] http://www.pci.unizh.ch/e/documents/Spektrum%20elektromagnetische%20Strahlung.jpg
10.06.2007 15:00 Uhr.
[6] http://www.3dchem.com/inorganics/NaCl-poly.jpg 10.06.2007 16:00 Uhr.
[7] M. Cotrait, C. R. Acad. Sci., Ser. C. (Chim), 1969, 269, 1848.
[8] G. M. Sheldrick, Program for the Solution of Cystal Structures, Göttingen
1997.
[9] G. M. Sheldrick, Program for the Refinement of Crystal Structures, Göttingen 1993.
[10] L. J. Farrugia, J. Appl. Cryst. , 1999, 32, 837-838
[11] http://www.chem.gla.ac.uk/~louis/software/wingx/ 10.06.2007 16:00 Uhr.
[12] http://shelx.uni-ac.gwdg.de/SHELX/ 10.06.2007 16:00 Uhr.
[13] http://www.ic.cnr.it/sir2004.php 10.06.2007 16:00 Uhr.
[14] www.axco.com.au/lib/atl001.html 10.06.2007 17:00 Uhr
[15] http://www2.chemie.uni-halle.de/anorg/ak/merzweiler/apparate.htm
10.06.2007 18:00 Uhr
53