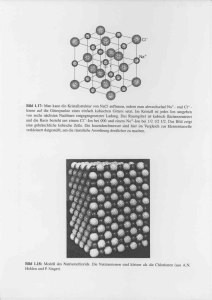
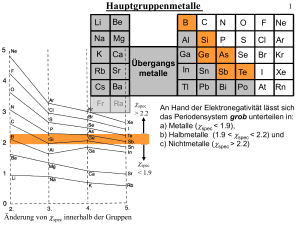
Aufgabe 1: Bestimmen sie die Punktgruppen (Schoenfliess und H

Aufgabe 1:
Bestimmen sie die Punktgruppen (Schoenfliess und H.-M.) von
a) PF5
b) C2H6
c) [Ni(CN)4]2d) Biphenyl in der Gasphase
e) [Co(en)3]3+
Welche dieser Punktgruppen sind für chirale Molekuele geeignet?
Aufgabe 2:
Wie lautet die dritte Pauling-Regel und warum ist sie relativ zuverlässig? Warum ist ZrI3 eine
Ausnahme?
Aufgabe 3:
Kristalle von GeS sind orthorhombisch mit a = 10.47, b = 3.64, c = 4.30 Å. In der Zelle
befinden sich vier Ge Atome auf ±(0.622 0.250 0.627; 0.122 0.250 0.873) und vier S Atome
auf ±(0.349 0.250 0.001; 0.849 0.250 0.499).
a)
Berechnen Sie das Volumen der Elementarzelle und die Dichte des Kristalls.
b)
Zeichnen Sie die Projektion der Struktur mit c senkrecht zur Papierebene.
c)
Beschreiben Sie die Koordinationsgeometrie von Ge und S.
d)
Wie lang sind die zwei kuerzesten unabhaengigen GeS Abstaende.
Aufgabe 4:
a)
Definieren Sie den Begriff dichteste Packung.
b)
Welche Luecken und wie viele findet man in einer kubisch-flaechenzentrierten
Elementarzelle?
c)
Welche Koordinationszahlen und -polyeder findet man in ccp-Strukturen?
d)
Beschreiben Sie die NaCl-Struktur als Variante der dichtesten Packung.
e)
Definieren Sie den Begriff Raumerfuellung und berechnen Sie selbige fuer den ccpFall.
Aufgabe 5:
a)
Entscheiden Sie mit Hilfe der erweiterten 8-N Regel, ob folgende Verbindungen
polyanionisch, polykationisch oder einfach ionisch sind:
Be2C, Mg2C3, ThC2, Li2Si, In4Se3, KSb, Nb3Cl8
b)
c)
Wie ist die VEK definiert?
Wie kann man die Struktur von polyanionischen Verbindungen (innerhalb gewisser
Grenzen) vorhersagen?