Impedanzspektroskopie an einem Sauerstoff

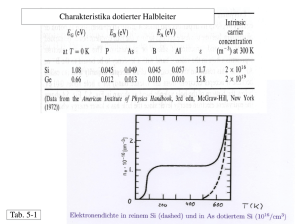
Fortgeschrittenen-Praktikum
Physikalische Chemie
Impedanzspektroskopie
an einem Sauerstoffionenleiter
Institut für Physikalische Chemie
Arbeitskreis Prof. Dr. Christian Hess
Betreuer:
Prof. Dr. Christian Hess
Eduard-Zintl-Institut für Anorganische und Physikalische Chemie, TU Darmstadt,
Petersenstr. 20, 64287 Darmstadt
Kontakt: Tel.: 06151-164925, e-mail: [email protected]
Der Versuch findet im Grundpraktikum der Physikalischen Chemie Raum 401 im 4. OG von Gebäude
L204 (Petersenstr. 20) statt. Nach Ankunft melden Sie sich bitte zuerst in Raum 424. Zur
Vorbereitung: Einführungsvorlesung, Stichpunkte, Versuchsbeschreibung, Literaturliste.
Inhaltsverzeichnis
1.
Einführung ....................................................................................................................................................1
1.1.
1.2.
1.3.
1.4.
1.5.
Leitfähigkeit in ionischen Kristallen ........................................................................................................1
Impedanzspektroskopie............................................................................................................................1
Ersatzschaltbilder .....................................................................................................................................4
Keramische Sauerstoffionenleiter ............................................................................................................6
Vorbereitung ............................................................................................................................................8
2.
Beschreibung des Versuchsaufbaus ............................................................................................................9
3.
Versuchsdurchführung ..............................................................................................................................10
4.
Auswertung .................................................................................................................................................10
5.
Literatur ......................................................................................................................................................10
6.
Anhang.........................................................................................................................................................11
6.1.
6.2.
Hilfreiche Formeln .................................................................................................................................11
Kröger-Vink Notation ............................................................................................................................11
I
1. Einführung
1.1. Leitfähigkeit in ionischen Kristallen
In ionischen Kristallen kann der Ladungstransport über verschiedene Ladungsträger erfolgen wie z.B.
Elektronen in Metallen und n-Halbleitern, Elektronenlöchern in p-Halbleitern oder Ionen in ionischen Leitern.
Normalerweise sind mehrere Mechanismen am Ladungstransport beteiligt und ihre partiellen Leitfähigkeiten σi
addieren sich zur Gesamtleitfähigkeit σ.
Die Leitfähigkeit in Halbleitern und ionischen Leitern hängt nach Gl. 1 von der Ladungsträgerkonzentration ci
und mechanischen Mobilität bi ab (zi = Ladung, F = Faraday-Konstante).
σ i = c i b i z i2 F 2
(1)
In Halbleitern sind die Ladungsträger die Elektronen oder Elektronenlöcher, deren Konzentration mit der
Temperatur ansteigt (Bändermodell). Die Mobilität der Elektronen ändert sich mit der Temperatur nur mäßig.
In Ionenleitern bewegen sich die Ionen, indem sie von einer Fehlstelle zur nächsten springen. Die Konzentration
der Fehlstellen und somit die Ionenleitfähigkeit steigt mit der Temperatur an. Im Gegensatz zu Halbleitern ist
auch die Mobilität der Ladungsträger stark temperaturabhängig. Der Grund dafür ist eine Aktivierungsenergie,
die für den Platztausch zwischen einem Ion und einer Fehlstelle nötig ist. Die Mobilität der Ionen ist mit dem
Diffusionskoeffizienten Di über die Einstein-Gleichung D i = b i RT verknüpft, wobei mit Gl. 1 die NernstEinstein-Gleichung (Gl. 2) folgt.
σi =
Di (T) ⋅ ci 2 2
zi F
RT
(2)
⎛ EA ⎞
⎟ und Gl. 2, kann
⎝ RT ⎠
Mit Hilfe der Temperaturabhängigkeit des Diffusionskoeffizienten D(T) = D o ⋅ exp⎜ −
die Temperaturabhängigkeit der Leitfähigkeit beschrieben werden (Gl. 3).
⎛ E ⎞
Do ⋅ exp⎜ − A ⎟ ⋅ ci
⎝ RT ⎠ z 2 F2
σi =
i
RT
(3)
1.2. Impedanzspektroskopie
In der Impedanzspektroskopie wird der frequenzabhängige Wechselstromwiderstand einer Probe gemessen, um
dynamische Prozesse von geladenen Teilchen zu untersuchen. Dadurch können Materialkonstanten
(Leitfähigkeit, dielektrische Konstante), Grenzflächenprozesse und die Kapazität von Grenzflächen bestimmt
werden. Beispielsweise kann somit zwischen den verschiedenen Teilprozessen (bulk-Leitfähigkeit,
Korngrenzleitfähigkeit, usw.) der Leitfähigkeit unterschieden werden. Da sich die Teilprozesse zeitlich
unterscheiden, können durch die Frequenzerhöhung einer angelegten oszillierenden Wechselspannung einzelne
Teilprozesse ausgeschaltet werden, da diese nicht mehr schnell genug folgen können.
Um Impedanzspektroskopie (IS) zu betreiben, muss bekannt sein wie sich Strom und Spannung in einer
elektronischen Schaltung bei Wechselstrom verhalten. Bei direkter Strommessung können die Ströme und die
Spannung über das Ohmsche Gesetz beschrieben werden. Dieses kann auch bei Wechselstrommessungen
angewendet werden, wenn nur ideale Widerstände vorhanden sind. Wenn Kapazitäten (Kondensatoren) oder
Induktionen (Spulen) in der Schaltung vorhanden sind, oszilliert der Strom und die Spannung nicht mehr in
Phase (Fig. 1).
Impedanzspektroskopie
1
U[V]
0
I[mA]
ϕ
2
4
6
8
10
ω t [ms]
Fig. 1: Strom – Spannung – Zeit - Abhängigkeit und Phasenwinkel.
In einer direkten Stromschaltung hat ein ohmscher Drahtwiderstand einen Widerstand R, eine ideale Spule einen
Widerstand von null Ohm und ein Kondensator einen unendlich hohen Widerstand. Wenn eine
Wechselspannung an der Schaltung angelegt wird, wird der Widerstand von beiden Elementen
frequenzabhängig. Zum Beispiel schwächt eine Spule den Strom (Induktionsgesetz). Deshalb ist es nicht
möglich den Strom und die Spannung nur durch das Ohmsche Gesetz und reelle Zahlen zu beschreiben. Für die
Beschreibung von U und I müssen komplexe Zahlen verwendet werden.
Der Strom und die Spannung kann durch die folgenden Gleichungen mit Hilfe der Kreisfrequenz ω zeitabhängig
ausgedrückt werden:
U = U 0eiωt und I = I 0eiωt +iΦ
(4), (5)
Der komplexe Widerstand, die sogenannte Impedanz Z, ist definiert gemäß:
Z=
U U 0 −iΦ
=
e
I
I0
(6)
Die Impedanz kann in den Realteil Z´ und den Imaginärteil Z´´ über die Eulersche Formel
( e ix = cos x + i sin x ) aufgespalten werden:
Z = Z´ + i Z´´ mit Z´=
U0
U
cosΦ und Z´´= − 0 sinΦ
I0
I0
(7)
Impedanzspektroskopie bezeichnet die Messung der Impedanzen bei verschiedenen Frequenzen. Zum besseren
Verständnis wird dies für eine einfache RC-Schaltung erklärt (Fig. 2).
Impedanzspektroskopie
2
U = Uoeiωt
~
I = Ioeiωt+iφ
C
R
Fig. 2: RC-Schaltung.
Wenn die angelegte Spannung U eine sehr niedrige Frequenz hat, ist der Kondensator schon zu Beginn der
Oszillationsperiode komplett geladen und für den Strom blockiert. Der gesamte Strom läuft durch den
Widerstand. Im anderen Extremfall bei sehr hohen Frequenzen wechselt die Richtung des Stroms bevor eine
relevante Ladung am Kondensator entstehen kann. Der Widerstand des Kondensators nähert sich gegen null und
der gesamte Strom fließt durch den Kondensator. Der Widerstand des Kondensators kann mathematisch wie
folgt hergeleitet werden. Die Ladung Q am Kondensator mit der Kapazität C ist:
Q = C⋅U
(8)
Da der Strom als Ladung pro Zeit definiert ist, resultiert mit Gl. 4 die folgende Beziehung:
I=C
d
(U 0eiωt ) = iωCU 0eiωt
dt
(9)
Mit Gl. 6 folgt für die Impedanz des Kondensators:
ZC =
1
iωC
⎛ 1
=
Wenn Kirchhoffs Gesetze für Parallelschaltung ⎜
⎜Z
⎝ ges
(10)
⎛
⎞
1 ⎞⎟
∑i Z ⎟ und Reihenschaltung ⎜⎝ Z ges = ∑i Zi ⎟⎠ für die
i ⎠
Impedanzen gültig sind, lautet die totale Impedanz der Schaltung:
1
1
1
= +
1
Z RC R
iωC
Wird der Zähler und Nenner von Gl. 11 erst mit
Z RC =
Impedanzspektroskopie
→
Z RC =
1
1
+ iωC
R
(11)
1
2
− iωC und dann mit R multipliziert, ergibt sich:
R
R
ωCR 2
−
i
1 + (ωCR) 2 1 + (ωCR) 2
(12)
3
In Gl. 12 ist leicht die Impedanz für die beiden Extremfälle ω = 0 und ω = ∞ zu sehen. In beiden Fällen ist der
Imaginärteil der Impedanz gleich null. Nur für mittlere Frequenzen ist der Imaginärteil der Impedanz ungleich
null, was anhand eines 3D-Graphen gezeigt werden kann (Fig. 3).
-Z´´
ω
Z´
lo
)
2π
/
ω
g(
Fig. 3: 3D-Graph des Impedanzspektrums einer einfachen RC-Schaltung.
Die Projektion in die Z´-Z´´-Ebene, der sogenannte Nyquist-Plot, wird für gewöhnlich gezeigt. Für eine RCSchaltung ist diese Projektion ein Halbkreis. Von der Projektion kann der Wert des Widerstandes R als der
Kreisdurchmesser abgelesen werden, und da am Scheitelpunkt des Kreises ω =
1
gilt, kann daraus ebenfalls
RC
die Kapazität C bestimmt werden.
1.3. Ersatzschaltbilder
Ein Impedanzspektrum kann aus mehreren Elementen wie Halbkreisen und Linien bestehen, die durch
komplexe Ersatzschaltbilder repräsentiert werden können. Für die Interpretation eines Spektrums muss ein
Schaltbild gefunden werden, das zum Experiment korrespondiert, indem ein physikalisches Modell (elektrische
Doppelschicht, Korngrenzen, etc.) angenommen wird. Ein Standardmodell (Fig. 4) für polykristalline Proben
wurde von Bauerle1 entwickelt. Dieses Modell beschreibt einen reinen Ionenleiter.
Cdl
Cb
Cgb
dl: Doppelschichtkapazität
d: Widerstand an der
Grenzfläche Elektrode/Probe
b: bulk
Rd
Rb
Rgb
gb: Korngrenze
Fig. 4: Ersatzschaltbild nach Bauerle.
Impedanzspektroskopie
4
Ein Problem bei der Interpretation ist, dass verschiedene Ersatzschaltbilder existieren, deren Impedanzspektren
nicht unterscheidbar sind. Zum Beispiel zeigt das Ersatzschaltbild in Fig. 5 qualitativ die gleichen Spektren wie
das in Fig. 4. Es ist unmöglich durch Impedanzspektroskopie zwischen diesen beiden Schaltbildern zu
unterscheiden.
R1
R2
R3
C1
C2
C3
Fig. 5: Alternatives Ersatzschaltbild.
Fig. 6 zeigt das simulierte Impedanzspektrum für beide Schaltbilder. Es zeigt exemplarisch zwei weitere
Probleme, die bei der Auswertung von Impedanzspektren auftreten können. Es ist möglich, dass zwei
Halbkreise überlappen können oder ein Halbkreis teilweise außerhalb des Messbereichs des Messinstrumentes
liegt.
2,5
-Z´´ [MΩ]
2,0
1,5
1,0
0,5
0,0
0,0
0,5
1,0
1,5
2,0
2,5
Z´ [MΩ]
Fig. 6: Nyquist-Graph für das Schaltbild in Fig. 4 und 5 (Zahlen = log(f/Hz)).
Wenn das Spektrum als 3D-Graph (Fig. 7) gezeichnet wird, kann die Frequenzabhängigkeit viel besser gesehen
werden als im Nyquist-Plot. Der kleine Halbkreis liegt bei ganz anderen Frequenzen verglichen mit den anderen
Halbkreisen, was im 2D-Plot nicht zu erkennen ist.
Impedanzspektroskopie
5
-Z´´
ω
Z´
lo g
2
ω/
π)
(
Fig. 7: 3D-Graph des Impedanzspektrums eines Bauerle Ersatzschaltbildes.
In einer Probe müssen normalerweise nicht alle diese Widerstände oder Kapazitäten betrachtet werden. Manche
Elemente sind entweder physikalisch nicht existent oder zu klein. Einkristalle haben keine Korngrenzen und in
reinen Ionenleitern gibt es keine und/oder sehr kleine elektronische Leitfähigkeit.
1.4. Keramische Sauerstoffionenleiter
Das wahrscheinlich am besten bekannte und deshalb am häufigsten verwendete Material ist Yttrium dotiertes
Zirconiumdioxid. Aus dem Phasendiagramm (Fig. 8) geht hervor, dass die monokline Form von
Zirconiumdioxid bis 1200°C stabil ist, zwischen 1200°C und 2500°C wird die tetragonale Phase stabil und über
2500°C ist kubisches ZrO2 thermodynamisch stabil. Diese Phasen müssen bei tieferen Temperaturen stabilisiert
werden, da der Übergang zu der monoklinen Phase mit einer Änderung im Zellvolumen einhergeht, und die
Probe dadurch zerstört werden kann. Die Stabilisierung wird meistens durch Zugabe von Y2O3 (YSZ) oder CaO
(CSZ) erreicht.
Impedanzspektroskopie
6
Y2O3-ZrO2
3000
liquid
2500
2000
cubic
(C)
tetragonal
(T)
T
+
C
T [°C] 1500
1000
M
T+C
+
T
monoclinic
(M)
500
M+C
0
90
Y2O3
92
94
96
n [mol %]
98
100
ZrO2
Fig. 8: Phasendiagramm des Systems ZrO2-Y2O3.
Auf Grund der niedrigeren Valenz der Yttrium- oder Calciumionen wird ein höherer Anteil an Fehlstellen im
Sauerstoffionengitter produziert (Gl. 13, „Kröger-Vink Notation“) und folglich wird auch eine höhere
Ionenleitfähigkeit erzielt.
Y2O3 (s) → 2YZr′ + 3O ox + Vo••
(13)
Durch den Übergang von Sauerstoff aus dem Gitter in die Gasphase (Gl. 14), werden Elektronen und
Fehlstellen als Defekte produziert. Ihre Konzentration hängt vom Sauerstoffpartialdruck ab.
Impedanzspektroskopie
7
1
O ox → O 2 (g) + 2e′ + Vo••
2
(14)
Für die Anwendung als Sauerstoffionenleiter ist eine Überführungszahl von ca. eins für die Sauerstoffionen
wünschenswert, so dass der Ladungstransport durch Elektronen oder Elektronenlöcher vernachlässigt werden
kann. Deshalb ist es ziemlich wichtig die partiellen Leitfähigkeiten in Abhängigkeit von der Temperatur und
dem Sauerstoffpartialdruck zu kennen (vgl. Fig. 9).
ZrO2 (+10 mol % Y2O3)
σ [Ω-1 cm-1]
σO- 10-2
1200°
1000°
1100°
900°
-4
10
σp
σn
10-6
10-10
10-20
10-30
p(O2) [atm]
Fig. 9: Partielle Leitfähigkeiten in YSZ.
Für technische Anwendungen von YSZ in Lambdasonden (Kontrolle des Luft/Kraftstoff-Gemisches im Auto,
Stahlherstellung) oder Brennstoffzellen existiert eine Temperaturbegrenzung. Nur bei Temperaturen über 600°C
gilt das Gleichgewicht von Gl. 14 und die partielle Sauerstoffionenleitfähigkeit ist groß genug. Deshalb ist die
Anwendung von YSZ auf Temperaturen über 600°C begrenzt. Um diese Begrenzung zu umgehen, werden
andere Materialien wie La1-xSrxGa1-yMgyO3-(x+y)/2 (LSGM) oder Scandium dotiertes Cerdioxid getestet, weil sie
vielversprechende Eigenschaften besitzen, so dass sie bei zukünftigen Anwendungen als Ersatz für YSZ dienen
könnten.
In der Forschung wird YSZ auch bei Sauerstofftitrationszellen eingesetzt. Diese Zellen können für die selektive
Titration von Sauerstoff in und aus der Zelle und für die simultane Messung des Sauerstoffpartialdruckes
verwendet werden. Dies ist eine einfache Möglichkeit, um Phasendiagramme zu untersuchen.
1.5. Vorbereitung
•
•
•
•
•
•
•
Leitfähigkeitsmechanismen
Wechselstromschaltungen
Impedanzspektroskopie
Stabilisiertes Zirconiumdioxid
Feste Elektrolyte
Defekte
Nicht-linearer Fit (Methode der kleinsten Quadrate)
Impedanzspektroskopie
8
2. Beschreibung des Versuchsaufbaus
Im Experiment wird YSZ (ZrO2 mit 9% Y2O3 - Dotierung) mit Hilfe der Impedanzspektroskopie untersucht.
Probengeometrie:
A = 3 mm x 4 mm
l = 5 mm
Die Impedanzspektren werden mit einem HP 4284a Impedanzanalysator gemessen. Die Probe ist in einem
Rohrofen mit Thermostat platziert. In Fig. 10 ist eine Abbildung des Probenhalters zusammen mit der Probe zu
sehen.
Fig. 10: Foto des Probenhalters mit der YSZ Probe.
Die gesamte Messanordnung (Leitungen, Probenhalter) ist geschützt. Der Aufbau ist in Fig. 11 und Fig. 12 zu
sehen. Die Kontrolle der Frequenzvariation und der Datenerfassung wird über den Computer gesteuert.
Fig. 11: Experimenteller Aufbau.
Impedanzspektroskopie
9
Fig. 12: Foto der elektrischen Leitungen des Probenhalters.
3. Versuchsdurchführung
Zur Überprüfung des Impedanzanalysators werden verschiedene RC-Schaltungen mit bekannten Widerständen
und Kapazitäten gemessen.
Das YSZ wird auf 420°C geheizt. Wenn die Temperatur der Probe konstant ist, kann die erste Messung gestartet
werden. Der Frequenzmessbereich erstreckt sich von 1kHz bis 6000kHz bei einer Spannungsamplitude von
0,1V. Die Messung sollte so oft wiederholt werden, bis sich das Impedanzspektrum nicht mehr verändert. Am
Ende der Messung kann die nächsttiefere Temperatur an der Ofenheizkontrolle eingestellt werden. Sobald die
Temperatur der Probe wieder konstant ist, kann das nächste Spektrum aufgenommen werden usw. Insgesamt
sollen sieben Messungen zwischen 420°C und 360°C in Abständen von 10°C durchgeführt werden.
Die Messdaten sollten auf dem Laufwerk gespeichert werden und später auf eine Diskette übertragen werden.
Die Auswertung kann zu Hause mit Origin oder einer ähnlichen Anwendung durchgeführt werden. Alternativ
kann ein Computer im Praktikum mit einer installierten Origin-Version benutzt werden – bitte den Assistenten
fragen, wenn dies erwünscht ist.
4. Auswertung
1. Überprüfung des Impedanzanalysators mit Hilfe bekannter RC-Ersatzschaltbilder.
2. Temperaturabhängige Messung und Analyse der Impedanzspektren der Probe bei sieben verschiedenen
Temperaturen von 360°C bis 420°C in Stufen von 10°C. Schätzen Sie die Aktivierungsenergie für die
Sauerstoffionenleitfähigkeit der Probe ab und vergleichen Sie sie mit Literaturdaten.
3. Wenn Sie ein Spektrum unter Sickstoffatmosphäre aufnehmen würden, was würden Sie erwarten?
(Diskutieren Sie im Protokoll)
4. Mit Hilfe von Gl. 12 und der mathematischen Kreisgleichung soll gezeigt werden, dass die Projektion in
die Z´-Z´´-Ebene wirklich ein Halbkreis ist.
5. Schreiben Sie die Gleichung für die Beimischung von SrO und MgO in LaGaO3 mit der korrekten
Kröger-Vink-Notation auf.
5. Literatur
1. J. E. Bauerle, J. Phys. Chem. Solids, 1969, 30, 2657.
2. A. R. West, Solid state chemistry and its applications, Wiley, l984.
3. W. Göpel, C. Ziegler, Einführung in die Materialwissenschaften, Teubner, 1996.
4. D. Ende, K. Mangold, Impedanzspektroskopie, ChiuZ, 1993, 27, 134-140.
Impedanzspektroskopie
10
6. Anhang
6.1. Hilfreiche Formeln
2
2
2
Kreisgleichung: r = (x – xM) + (y – yM) mit Radius r und Kreismittelpunkt (xM, yM).
Kreisfrequenz ω: ω = 2π ⋅ f mit Frequenz f.
Leitfähigkeit der Probe σ: σ =
1 l
⋅ mit Widerstand R, Fläche A und Abstand l der Kontakte.
R A
2
2
Trigonometrischer Pythagoras: sin x + cos x = 1.
2
2
Plus-Minus-Formel: (a + b) · (a – b) = a – b .
2
2
Plus-Minus-Formel für komplexe Zahlen: (a + ib) · (a – ib) = a – i b
2
2
= a +b
2
.
6.2. Kröger-Vink Notation
Punktdefekte in Kristallen lassen sich mit einer von F.A. Kröger und H.J. Vink eingeführten Notation
beschreiben. Da die Gitterbausteine in (perfekten) Ionenkristallen eine dem Element und der Kristallstruktur
entsprechende Ladung besitzen, wird in der Kröger-Vink-Notation bei Defekten die jeweilige Ladungsdifferenz
zum ideal besetzten Gitterplatz betrachtet. In der Kröger-Vink Notation werden Gitterdefekte gleich behandelt
wie chemische Spezies (Atome und Ionen).
Hat z.B. in Zirconiumdioxid das Zirconium-Kation den idealen Ionisierungsgrad 4+ (Zr4+), so bedeutet dies in
dieser Notation, dass es die Differenz Null zum Gitterplatz besitzt. Wird es jedoch durch Y3+ ersetzt, so hat
dieses die Ladung 1- verglichen zum ideal besetzten Gitterplatz.
Grundsätze für die Formulierung von Reaktionsgleichungen von Defektreaktionen:
1. Elektroneutralität: Der gesamte Körper muss elektrisch neutral bleiben.
2. Massenerhaltung: Die gesamte Masse der an der Reaktion beteiligten Atome/Ionen muss konstant
bleiben.
3. Platzverhältnis: Die Anzahl an Kationenplätzen (K) einer Verbindung KxAy muss immer im richtigen
Verhältnis zur Anzahl der Anionenplätze (A) stehen.
Symbol
VK′′
Bedeutung
Kation K oder Anion A auf eigenem Gitterplatz d.h. gegenüber dem idealen
Gitter neutral (x).
Kationenleerstelle mit der gegenüber dem idealen Gitter effektiven Ladung 2- (″).
VA•
Anionenleerstelle mit der gegenüber dem idealen Gitter effektiven Ladung 1+ (•).
K i•••
A′K
Interstitielles Kation mit der effektiven Ladung 3+ (•••).
K Kx , A Ax
YZr′
Sox
(Ce′Ce Vo•• )•
e′
h•
Interstitielles Anion mit der effektiven Ladung 1- (′).
Substituiertes Yttrium-Kation (3+) auf Zirkonplatz (4+) mit der effektiven
Ladung 1- (′).
Substituiertes Schwefel-Anion (2-) auf Sauerstoffplatz (2-) mit der effektiven
Ladung 0 (x).
Assoziierter Defekt (einfach reduziertes Cer-Kation (3+) auf Ce4+ Platz assoziiert
mit einer Sauerstoffleerstelle (Vo•• ) auf O2- Platz). Der gesamte Defekt hat die
Ladung 1+ (•).
Elektron
Loch
Tab. 1: Übersicht über Kröger-Vink-Notation.
Impedanzspektroskopie
11