Elektrische Feldstärke und Oberflächenladung bei Gleichströmem

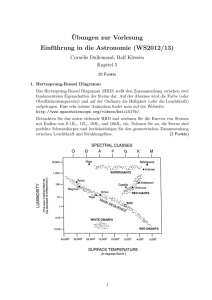
Abbildung 1: Vektorfelddarstellung des elektrischen Feldes, das in einem langen geraden
Draht durch Oberflächenladungen linear mit dem Ort variierender Dichte erzeugt wird.
Elektrische Feldstärke und
Oberflächenladung bei Gleichströmem
U. Backhaus
30. November 2009
Inhaltsverzeichnis
1 Einleitung
2
2 Qualitative Überlegungen
2
3 Berechnungen für ein langes gerades Kabel
3.1 Analytische Rechnung . . . . . . . . . . . .
3.2 Numerische Berechnungen . . . . . . . . . .
3.2.1 Algorithmus . . . . . . . . . . . . . .
3.2.2 Ergebnisse . . . . . . . . . . . . . . .
3.3 Folgerungen . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
4
6
6
6
8
4 Ursache und Wirkung
10
5 Schlussfolgerungen
11
Literatur
12
1
1
Einleitung
Im Schulfach Physik, aber auch in einführenden Physikkursen an der Universität werden Elektrostatik und Stromkreiselektrik als scheinbar völlig unabhängige Gebiete der
Physik behandelt: Die Eigenschaften elektrischer Stromkreise werden mit Begriffen wie
Stromstärke und Spannung und mit den Kirchhoff’schen Gesetzen beschrieben, in der
Elektrostatik spielen Coulomb-Wechselwirkungen die entscheidende Rolle, die jedoch kaum
bei der Analyse von Stromkreisen angewendet werden (siehe z. B. Sherwood et al [7], dort
viele weitere Quellen). Dabei wird die Chance vertan, die unterschiedlichen Bereiche der
Elektrodynamik als eng aufeinander bezogen ( vernetzt“) zu vermitteln und das Verständ”
nis der in verschiedenen Gebieten (auch der Mechanik) eingeführten Begriffe und Gesetze
zu vertiefen.
Immer wieder werden deshalb Vorschläge gemacht, die Rolle elektrostatischer Aufladungen in Gleichstromkreisen in den Blickpunkt zu rücken. Den ersten Vorschlag in
Deutschland machte dazu, glaube ich, A. Walz [9], der auch in das Buch von Muckenfuß
et al. [5] aufgenommen wurde. Ausgangspunkt dieser Vorschläge sind Fragen der folgenden
Art:
• Wie verbiegt ein stromführendes Kabel das elektrische Feld eines geladenen Kondensators (oder einer anderen Quelle) so, dass es innerhalb des Kabels axial verläuft?
• Wie wird Ladung, wie werden die Elektronen durch ein widerstandsbhaftetes Kabel
getrieben?
Hier soll der grundlegende Gedankengang skizziert und analysiert werden, der dazu
führt, Oberflächenladungen als Ursache für den elektrischen Strom anzusehen. Motivation
für diese Untersuchung ist einerseits die Übereinstimmung mit dem Ziel, zu einer konsistenten Beschreibung von Elektrostatik und Stromkreiselektrik zu gelangen, andererseits
aber die Skepsis der Rolle gegenüber, die den Oberflächenladungen dabeu zugeschrieben
wird.
2
Qualitative Überlegungen
Sherwood et al. (a.a.O.) verwenden zur Motivation einen etwas gewundenen Stromkreis,
über den ein geladener Kondensator entladen wird (Abb. 2). In dem Kabel ist (wegen
~ das elektrische Feld teilweise dem ursprünglichen, d. h. vom geladenen Kon~j = σ E)
densator allein erzeugten Feld entgegen gerichtet. Diese Richtungsumkehr werde durch
Oberflächenladungen erzwungen, die sich beim Einschaltvorgang in den Biegungen sammeln (Abb. 3, links). Auch in den geraden Kabelabschnitten werde der Strom nicht durch
die Ladung auf den Kondensatorplatten angetrieben, sondern durch Oberflächenladungen,
deren Dichte von der positiv geladenen zur negativen Kondensatorplatte (im Wesentlichen) gleichmäßig abnehme. Am deutlichsten zu erkennen ist das in Abbildung 3, rechts
an dem rechten senkrecht verlaufenden Kabelstück.
Um den Antrieb der Elektronen durch Oberflächenladung abnehmender Dichte verständlich zu machen, wird ein (unendlich) langer gerader Draht betrachtet (Haertel [4], auf
2
Abbildung 2: Während der Kondensator entladen wird, zeigt da elektrische Feld innerhalb
des Kabels immer in axiale Richtung. (aus [7])
Abbildung 3: Das Feld wird in Biegungen von Oberflächenladungen umgebogen“ (links)
”
und in geraden Kabelstücken durch Oberflächenladung abnehmender Dichte erzeugt. (aus
[7])
3
Abbildung 4: Ein konstanter Ladungsdichtegradient auf der Oberfläche eines langen gerade Drahtes erzeugt auf der Achse ein axiales elektrisches Feld konstanter Feldstärke (aus
[4])
den Sherwood et al. sich beziehen) und begründet, dass auf der Symmetrieachse dieses
Drahtes ein axiales Feld entsteht, dessen Feldstärke konstant ist, wenn der Gradient der
Oberflächenladungsdichte konstant ist (Abb. 4). Auch außerhalb der Achse sei das elektrische axial gerichtet, weil sich andernfalls die Oberflächenladung so umverteilen würde,
dass die radiale Feldkomponente verschwinde.
Diese Argumentation soll quantitativ geprüft werden.
3
Berechnungen für ein langes gerades Kabel
3.1
Analytische Rechnung
Der lange gerade Draht verlaufe in z-Richtung, sein Radius sei R. Die Oberflächenladungsdichte verändere sich linear mit dem Ort: σ = Cz.
Das elektrische Feld E an der Stelle z = 0 auf der Symmetrieachse kann berechnet
werden, indem man die Beiträge dE(z) bestimmt, die von Ringen mit der Breite dz an
der Stelle z erzeugt werden (Abb. 5):
1. Aus Symmetriegründen kompensieren sich alle Komponenten senkrecht zur Drahtachse. Zu berechnen ist deshalb nur die Axialkomponente:
1 dQ
~er
4π²0 r2
1 dQ z
dEz (z) =
4π²0 r2 r
σ(z)R zdz
=
2²0 r3
~
dE(z)
=
=⇒
2
(dQ = 2πRσ(z)dz)
(σ(z) = Cz)
z2
d
R2
z dz
CR
CR
=
3 =
2²0 (R2 + z 2 ) 2
2²0 ³
1+
³ ´
z
R
z2
R2
´3
Wie man leicht nachrechnet, hat diese Funktion ihre Extrema bei
√
bei z = ± 2R.
4
(1)
2
z
R
√
= ± 2, also
Abbildung 5: Jeder Ladungsring erzeugt auf seiner Achse ein axiales elektrisches Feld.
Sind zwei gleich weit entfernte Ringe entgegengesetzt geladen oder tragen sie Ladung
gleichen Vorzeichens aber unterschiedlichen Betrages, ergibt sich ein nicht verschwindendes Gesamtfeld.
2. Eine konstante Oberflächenladungsdichte erzeugt kein axiales elektrisches Feld, da
sich für jeden Punkt auf der Achse die Beiträge symmetrisch liegender Ringe gegenseitig kompensieren. Da durch Addition einer konstanten Oberflächenladungsdichte
der Nullpunkt der Funktion σ(z) an beliebige Stellen verschoben werden kann, gilt
das Ergebnis (1) für jede Stelle z0 :
Den größten√Beitrag zur Axialfeldstärke liefern die Oberflächenladungen
im Abstand 2R.
3. Um die Axialfeldstärke zu erhalten, müssen die Beiträge aller Ringe aufsummiert
werden:
Ez (0) =
Ã
Z ∞
CR
z
z2
dE(z)dz =
arsinh − 1 + 2
4²0
R
R
−∞
!− 1 ¯¯∞
2¯
¯
¯
¯
(2)
−∞
Wegen
³
arsinhx = ln x +
=⇒
lim arsinhx =
x→∞
√
x2 − 1
´
lim ln(2x) = ∞
x→∞
(3)
√
divergiert das Integral (2)1 : Zwar liefern die Oberflächenladungen im Abstand 2R
den größten (individuellen) Beitrag zur Axialfeldstärke. Die gegen null konvergierenden Beiträge der entfernten Ladungen führen trotzdem zu einer unendlich großen
Axialfeldstärke – unabhängig von der Größe der Oberflächenladungsdichte!
1
Zu diesem Ergebnis kann man auch gelangen,
¡ zohne
¢ das Integral explizit zu lösen: Für z → ∞ geht der
Beitrag einzelner Ringe in einen Ausdruck ∼ R
d
z
R über. Das Integral divergiert demnach logarithmisch.
5
Eigentlich ist an dieser Stelle bereits klar, dass die Rückführung des elektrischen Feldes
in einem stromführenden, widerstandsbehafteten Draht auf einen Gradienten der Oberflächenladungsdichte gescheitert ist. Trotzdem sollen weitere Argumente gesammelt werden, indem auch die Feldstärke außerhalb der Achse berechnet wird. Da das nicht (einfach)
möglich ist, wird die Feldstärke im folgenden Abschnitt numerisch berechnet.
3.2
3.2.1
Numerische Berechnungen
Algorithmus
Für jeden Aufpunkt ~r0 = (x0 , y0 , z0 ) wird die elektrische Feldstärke folgendermaßen berechnet:
1. Ein Stück eines Ringes an der Stelle ~r = (R sin φ, R cos φ, z) liefert den Beitrag
~ 0 (~r0 , z, φ) =
dE
1 σ(x)Rdφdz
(~r0 − ~r)
4πε0 |~r0 − ~r|3
2. Integration über den ganzen Ring ergibt den Beitrag des Ringes an der Stelle z:
~ r0 , z) =
dE(~
Z2π
~ 0 (~r0 , z, φ)
dE
0
3. Integration über alle“ Ringe ergibt dann die gesuchte Feldstärke an der Stelle ~r0 :
”
~ r0 ) = lim
E(~
zZ
0 +∆
∆→∞
z0 −∆
~ r0 , z)
dE(~
4. Wegen der Zylindersymmetrie kann x0 ≡ 0 gewählt werden. Bei der numerischen
Integration werden ∆φ = 1◦ und ∆z = 0.1R verwendet. Für den Querschnitt des
Kabels wird A = 1mm2 angenommen. Die Länge ∆ des bei der Berechnung der
Feldstärke berücksichtigten Kabelstücks kann frei gewählt werden.
3.2.2
Ergebnisse
Die Berechnung der Beiträge der einzelnen Ringe zur Axialfeldstärke und deren Integration (Abb. 6) zeigen das analytisch gewonnene Verhalten, insbesondere das logarithmische Divergieren der Axialfeldtstärke, wenn immer weiter entfernte Oberflächenladungen
berücksichtigt werden (siehe (2)).
In der Umgebung der Stelle z = 0, an der die Oberflächenladung ihr Vorzeichen
wechselt, ergibt sich ein näherungsweise homogenes axiales Feld (Abb. 1). Lässt man
dabei Feldlinien zeichnen (Abb. 7), erkennt man, dass die Homogenität des berechneten
Feldes mit wachsender Zahl berücksichtigter Ringe größer wird. Das ist (nach längerer
Verunsicherung!) klar: Die axiale Komponente des elektrischen Feldes wird immer größer,
während die Radialkomponente nahezu unabhängig von der Anzahl der Ringe ist.
6
dE
dE
-10
Eges/Eg
Beitraege benachbarter Ringe
aufsummierte Beitraege benachbarter Ringe
1.0
Beitraege benachbarter Ringe
aufsummierte Beitraege benachbarter Ringe
0.8
0.6
0.6
0.4
0.4
0.2
0.2
10
-150
-100
-50
(x-x0)/R
-0.2
50
100
150
(x-x0)/R
-0.2
-0.4
-0.4
-0.6
-0.6
-0.8
x0 = 0.0*R
Eg=Feldstaerke bei beruecks. Abstand=160*R
1.0
0.8
-0.8
x0 = 0.0*R
Eg=Feldstaerke bei beruecks. Abstand=160*R
-1.0
-1.0
Abbildung 6: Der Beitrag von je 20 (links) bzw. 160 Ringen zur Axialfeldstärke an der
Stelle x0 = 0, an der die Oberflächenladung ihr Vorzeichen wechselt. Angenommen wurde
ein linearer Abfall der Ladungsdichte.
Abbildung 7: Feldlinienbild in der Umgebung von z = 0. Das Bild wird umso homogener,
je mehr Ringe bei der Berechnung berücksichtigt werden
7
Eges/Eg
Er
100*Et
-1.5
-1.0
-0.5
0.5
1.0
1.5
y/R
Abbildung 8: Der Verlauf von Axial- und Radialkomponente des elektrischen Feldes über
den Drahtquerschnitt
Die Feldlinien beginnen und enden auf den Ladungen der Oberfläche, die das Feld
erzeugen. Die damit zwangsläufig (!) verbundenen Radialkomponenten widersprechen jedoch der Annahme einer konstanten Stromdichte. Außerdem fällt auf, dass das Ergebnis
nicht translationsinvariant ist – im Gegensatz zu der angenommenen Translationssymmetrie von Stromdichte und Feldstärke!
Abbildung 8 zeigt, dass die Axialkomponente des Feldes tatsächlich konstant (und
an der Oberfläche stetig) ist. Die Radialkomponente nimmt dagegen in der Nähe der
Oberfläche große Werte an (und zeigt an der Oberfläche den mit der Oberflächenladung
verbundenen Sprung)!
3.3
Folgerungen
Die Ansicht, zur Feldstärke im Innern des Drahtes trügen nur die Oberflächenladungen
in der Nähe“ bei, lässt sich nicht aufrecht erhalten. Bereits Coombes et al. [2] gelangen
”
zu der surprising answerthat an infinitely long long wire in which a steady current is flo”
wing has a vanishing surface charge density . . .“ (S. 450). Auch Sherwood et al. [7], S. 16)
bemerken die Divergenz des Integrals (2). Allerdings ziehen sie daraus, ohne das zu begründen, nicht den Schluss, den ganzen Ansatz zu verwerfen2 . Die mit der Ladung auf der
Oberfläche notwendig verbundene Radialkomponente des elektrischen Feldes erwähnen
sie nicht, obwohl sie von Härtel [4], auf den sie sich beziehen, nur mit windigen Argumenten beiseite gewischt werden: The forces perpendicular to the axis, however, have to
”
be zero because otherwise the electrons would move to the surface and redistribute until
there is no longer a force towards the surface.“ ([4], S. 3). Dieser Radialstrom würde dazu
führen, dass die Oberflächenladung null würde – wenn nicht andere Ladungen außerhalb
vorhanden wären, die die Radialkomponente kompensierten!
2
In das Buch konnte ich noch nicht sehen.
8
Abbildung 9: Elektrisches Feld (gestrichelt) und Energieströmung bei einem Koaxialkabel
(aus [8]): Innenkabel und Außenleiter sind gegensinnig geladen.
9
Abbildung 10: Wenn die Batterie das Lämpchen zum Leuchten bringt: Muss das Leuchten
bei Annäherung nicht heller werden? (aus [7])
In einem Buch von A. Sommerfeld ([8], § 17) wird der Energiefluss in einem Koaxialkabel behandelt (Abb. 9). Dazu muss zunächst das elektrische Feld im Zwischenraum
berechnet werden. Dabei werden auch die Ladungen auf dem Innenleiter erwähnt. Auf
diese Darstellung gehen, glaube ich, alle Vorschläge zurück, diesen Oberflächenladungen
größere Aufmerksamkeit zu widmen. Dabei wird jedoch übersehen, dass der Außenleiter
des Kabels entgegengesetzt geladen ist wie der Leiter im Innern. Diese Ladung auf dem
Außenleiter kompensiert nicht nur die Radialkomponente des elektrischen Feldes im Innern des inneren Kabels, sie sorgt auch für die erforderliche Translationsinvarianz, zwar
nicht für das elektrische Feld im Zwischenraum, aber für das Feld im Innern des Innenleiters! Der Außenleiter darf deshalb nicht einfach weggelassen werden. Die Ladungsdichte
auf dem Innenleiter verschwindet, wenn der Radius des Außenleiters unendlich groß wird!
Die Schwierigkeiten mit dem Zusammenhang zwischen Oberflächenladung und Stromdichte beruhen auf der Nichtberücksichtigung der Ladungen außerhalb des Kabels!
4
Ursache und Wirkung
Ich bezweifle, dass es bei Phänomenen, die gleichzeitig auftreten, sinnvoll ist, von Ursache und Wirkung zu sprechen: Sind die Oberflächenladungen die Ursache des elektrischen
Stromes im Kabel, oder werden sie (beim Einschaltvorgang) von dem Strom hervorgerufen? Mit einer solchen Kausalbeschreibung wird man dem komplexen Rückkopplungsprozess nicht gerecht, in dem sich der (quasi-) stationäre Zustand einstellt. Wenn sich dieser
Zustand eingestellt hat, lässt sich nur noch die Konsistenz feststellen: Ströme, Felder,
Ladungen und Kräfte passen zueinander!
Wenn es aber doch ein Kausalzusammenhang aufgestellt werden soll, scheint es mir
naheliegend, bei Feldlinien die Ladungen (besser: geladenen Körper), auf denen sie beginnen und enden, als ihre Ursache zu betrachten. In diesem Sinne wären dann doch die
Grenzflächenladungen zwischen Batterie und Kabel bzw. zwischen Kabel und Widerstand
die Ursache für das Längsfeld in Kabeln und Widerständen.
Wenn es sinnvoll ist, von Ursache und Wirkung zu sprechen, sollte man (vielleicht von
gewissen Ausnahmen abgesehen) erwarten, dass sich die Wirkungen ändern, wenn sich
ihre Ursachen verändern. Gerade das trifft aber in der Regel bei Oberflächenladungen und
Strömen nicht zu: In einem langen geraden Kabel eines Stromkreises ändern sich weder
Richtung noch Größe der Stromdichte, wenn die anderen Teile des Stromkreises bewegt
10
Abbildung 11: Computerberechnung der Feld- und Ladungsverteilung kurz nach Schließen
des Stromkreises (aus [6])
werden3 . Diese Bewegung hat aber in der Regel starken Einfluss auf die Verteilung der
Ladung auf der Oberfläche der Kabel. Zum Beispiel häuft sich negative Ladung an der
Stelle an, der der Pluspol der Quelle genähert wird4 .
Nachdem ich auf dieses Argument gekommen war und schon überlegte, wie ich es grafisch darstellen könnte, fand ich bei Parker [6] Computerberechnungen, die genau dieses
zeigen: Bei einem geraden Leiterstück nimmt die Dichte der Oberflächenladungen nicht
gleichmäßig ab. Vielmehr wird sie entscheidend von den geladenen Platten des Kondensators beeinflusst – ohne dass der Strom in dem Kabel davon Notiz nähme“ (Abb. 11)!
”
In dem Buch von Sommerfeld ([8]) wird kein Ursache-Wirkungs-Zusammenhang hergestellt, wie Sherwood et al. ([7]) nahe legen5 .
5
Schlussfolgerungen
• Die Vorstellung von Dichtegradienten der Oberflächenladung als Antrieb von Strömen
lässt sich m. E. nicht aufrecht erhalten. Dagegen spricht noch ein weiteres Argument,
das mir einfällt, während ich dies schreibe: Wie soll ich mir energetisch vorstellen,
dass ruhende Ladungen (und die soll man sich doch wohl vorstellen) Energie an die
fließenden Elektronen übertragen?
• Trotzdem finde ich die Rolle der Oberflächenladung bei der Verformung des elektrischen Feldes sehr lehrreich.
3
Eine entsprechende, häufig anzutreffende Fehlvorstellung bei Lernenden bildet einen Ausgangspunkt
der Überlegungen von Sherwood et al. (a.a.O., S. 3, siehe auch Abbildung 10)
4
Bei gleich bleibender Spannung zwischen dieser Stelle und dem Pluspol vergrößert sich bei Annäherung die Feldstärke zwischen ihnen – und damit die Ladung an der Oberfläche. Wäre es deshalb nicht
näher liegend, zwischen Oberflächenladung und Außenfeld eine kausale Beziehung herszustellen?
5
. . . the uniform electric field . . . is actually produced (Hervorhebung von mir) by a constant gradient
”
of surface charge density.“ ([7], S. 9)
11
• Für mich läge es (immer noch) näher, die Grenzflächenladungen als Ursache für
Strömung und Energiemsatz anzusehen. Das kann man sich auch energetisch besser
vorstellen; denn sie müssen ständig nachgeliefert werden. Allerdings bin ich eher
dagegen, Kausalzusammenhänge zu stark zu betonen.
• Je länger ich darüber nachdenke, desto mehr komme ich zu der Überzeugung, dass
die Bedeutung der Oberflächenladungen eher in ihrem Zusammenhang mit dem
Außenfeld liegt (und nur so tauchen sie bei Sommerfeld auf). Ihre Verteilung hängt
eng mit der Verteilung des elektrischen Feldes im Außenraum zusammen – und
damit mit den Details der Energieströmung.
• Dass diese Details jedoch (wie in Abbildung 10) keinerlei Einfluss auf die Energieverteilung im Stromkreis haben, ist mein hauptsächliches didaktisches Argument
gegen die Poynting-Darstellung von Energieströmungen.
Literatur
[1] Chabay, R. W., Sherwood, B. A.: Electric and Magnetic Interactions, Wiley: New
York 1995
[2] Coombes, C. A., Laue, H.: Electric fields and charge distributions associated with
steady currents, Am.J.Phys. 49/5, 450 (1981)
[3] Härtel, H.: A qualitative approach to electricity, Report # IRL87-0001 (Institute for
Research on Learning Palo Alto, CA, 1987)
(http://eric.ed.gov/ERICDocs/data/ericdocs2sql/content storage 01/
0000019b/80/1c/0a/29.pdf)
[4] Härtel, H.: Constant Electric Current and the Distribution of Surface Charges,
(http://www.astrophysik.uni-kiel.de/∼hhaertel/PUB/voltage IRL.pdf)
[5] Muckenfuß, H., Walz, A.: Neue Wege im Elektrikunterricht, Aulis: Köln 1997
[6] Preyer, N. W.: Transient behavior of simple RC circuits, Am.J.Phys. 70/12, 1187
(2002)
[7] Sherwood, B. A.; Chabey, R. W.: A unified treatment of electrostatics and circuits
(http://www.matterandinteractions.org/Content/Articles/circuit.pdf
(25.11.2009))
[8] Sommerfeld, A.: Theoretische Physik, Band III: Elektrodynamik, Harri Deutsch: Thun
1977
[9] Walz, A.: E-Felder um stationäre Ströme, Der Physikunterricht, Heft 2/1984, S. 61-68
[10] Walz, A.: Fields that accompany currents, in: Duit, R., Jung, W., v. Rhöneck, C.
(Eds.): Aspects of understanding electricity. Proceedings of an international workshop. IPN-Arbeitsberichte 59, Schmidt und Klaunig: Kiel 1985
12