1 Schwerewellen in Wasser

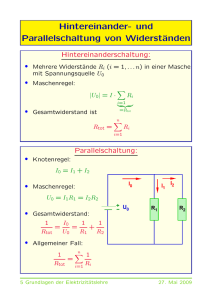
Seminar: Theoretische Mechanik, Dozent: Andreas Mielke
1
Schwerewellen in Wasser
Wir wollen eine ebene, monochromatische Wasserwelle mit sinusförmiger Oberflächenauslenkung
η(x, t) = a sin(ωt − kx)
(1)
beschreiben, mit der Oberflächenauslenkung η, der Amplitude a, der Kreisfrequenz ω = 2π
T
und der Wellenzahl k = 2π
.
Dabei
ist
T
die
Periode
und
λ
die
Wellenlänge.
In
unserem
λ
Koordinatensystem zeigt x in Ausbreitungsrichtung und z nach oben, die freie Oberfläche im
Gleichgewicht befindet sich bei z = 0 und der Boden unter dem Wasser bei z = −h.
Gesucht sind die Dispersionsrelation ω = ω(k) und das Geschwindigkeitspotential Φ, um
daraus Informationen über die Phasengeschwindigkeit c und das Geschwindigkeitsfeld der Fluid“teilchen“ v zu gewinnen.


λ
ω
c= =
T
k
;
v=

u(x, z, t)



0
= 

w(x, z, t)
∂Φ
∂x
0
∂Φ
∂z





(2)
Für inkompressible, wirbelfreie Fluide gilt die Laplacegleichung
∆Φ = 0
(3)
p ∂Φ 1 2
+
+ (u + w2 ) + gz = const.
ρ
∂t
2
(4)
sowie die Bernoulligleichung.
Die Konstante ist hierbei beliebig wählbar und, wenn wir sie gleich
die freie Oberfläche
∂Φ 1 2
+ (u + w2 ) + gη = 0
∂t
2
patm
setzen,
ρ
erhalten wir für
(5)
Als Randbedingung soll, die Vertikalkomponente der Teilchengeschwindigkeit am Boden
(z = −h) verschwinden
∂Φ w(z = −h) =
=0
∂z z=−h
(6)
und Teilchen“ die sich zur Zeit t0 an der freien Oberfläche befinden, für alle Zeiten t an der
”
Oberfläche bleiben.
1
∂η
∂η
+u
=w
∂t
∂x
(kinematische Randbedingung)
(7)
3, 5, 6 und 7 machen das zu lösende Gleichungssystem aus. Jedoch ist hierfür bisher keine
vollständige Lösung bekannt und es muss genähert werden.
In der linearen Wellentheorie gehen wir davon aus, dass die Amplitude der Wellen sehr viel
kleiner ist als ihre Wellenlänge, a << λ, und vernachlässigen daher alle Terme der Ordnung
O(a2 ). Da die Oberflächenauslenkung η, und die Horizontal- und Vertikalkomponente der
Teilchengeschwindigkeit u und w alle von der Größenordnung O(a) sind, sind die Terme 12 (u2 +
∂η
w2 ) in 5 und u ∂x
in 7 von der Ordnung O(a2 ) und können vernachlässigt werden.
∂Φ
= −gη
∂t
(8)
∂η
= w,
∂t
(9)
Die Annahme kleiner Amplituden ist gleichbedeutend mit der Aussage, dass die Oberflächenauslenkung
η eine kleine der Störung um die Gleichgewichtlage z = 0 ist. Das bedeutet, dass wir 8 und 9
um z = 0 entwickeln können
w(x, η, t) = w(x, 0, t) +
∂w
(x, 0, t)η + ...
∂z
∂ ∂Φ
∂Φ
∂Φ
(x, η, t) =
(x, 0, t) + ∂t (x, 0, t)η + ...
∂t
∂t
∂z
(10)
(11)
Auch hier ist der jeweils zweite Term auf den rechten Seiten von der Ordnung O(a2 ) und wird
vernachlässigt.
2
Damit ergibt sich das linearisierte Gleichungssystem
∂ 2Φ
∂ 2Φ
(x,
z,
t)
+
(x, z, t) = 0
∂x2
∂z 2
(12)
∂Φ
(x, z = 0, t) = −gη(x, t)
∂t
(13)
∂Φ
(x, z = −h, t) = 0
∂z
(14)
∂η
(x, t) = w(x, 0, t)
∂t
(15)
Wenn wir als Ansatz für das Potential
Φ(x, z, t) = A(z) sin(ωt − kx − ϕ0 )
(16)
∂ 2 A(z)
2
−k A(z) +
sin(ωt − kx − ϕ0 ) = 0
∂z 2
(17)
wählen, erhalten wir mit 12
Da der Vorfakor verschwinden muss, ergibt sich eine weitere Differentialgleichung für A(z) mit
der allgemeinen Lösung
A(z) = C1 cosh(kz + C2 )
(18)
∂Φ
∂A
(x, z = −h, t) =
(x, z = −h, t) sin(ωt − kx − ϕ0 ) = 0
∂z
∂z
(19)
Eingesetzt in 14 erhalten wir
Auch hier muss der Vorfaktor verschwinden und wenn wir 18 nach z ableiten und gleich Null
setzen
∂A
(x, z = −h, t) = kC1 sinh(k(−h) + C2 ) = 0
∂z
(20)
erhalten wir die Bedingung für die Konstante C2 . Da der Sinus Hyberbolicus verschwindet,
wenn sein Argument gleich Null ist, ergibt sich für C2 = kh und für das Potential
Φ = C1 cosh(k(z + h)) sin(ωt − kx − ϕ0 )
3
(21)
Dies können wir nun in 13 einsetzen
η(x, t) = −
1 ∂Φ
ω
(x, z = 0, t) = − C1 cosh(kh) cos(ωt − kx − ϕ0 )
g ∂t
g
(22)
Wiederum eingesetzt in 15 ergibt sich
∂η
ω2
=
C1 cosh(kh) sin(ωt − kx − ϕ0 ) =
∂t
g
∂Φ
w(x, z = 0, t) =
(x, z = 0, t) = kC1 sinh(kh) sin(ωt − kx − ϕ0 )
∂z
(23)
Daraus folgt
ω2
cosh(kh) = k sinh(kh)
g
(24)
beziehungsweise die Dispersionsrelation
ω 2 = gk tanh(hk)
(25)
Um aus 22 nun wieder die Anfangsgleichung 1 zu erhalten, setzen wir
ϕ0 = −
π
ω
und a = C1 cosh(kh)
2
g
(26)
woraus wir die Konstante C1 und schließlich mit 21 das Potential
Φ=
ag cosh(k(z + h))
cos(ωt − kx)
ω
cosh(kh)
(27)
erhalten.
Aus 25 können wir jetzt die Phasengeschwindigkeit herleiten
c=
ω
1p
=
gk tanh(hk)
k
k
4
(28)
Um dieses Ergebnis zu veranschaulichen, nähern wir noch für tiefes und flaches Wasser. Im
tiefen Wasser lassen wir h → ∞ gehen. Für den Tangens Hyberbolicus gilt lim tanh(hk) = 1,
h→∞
für die Phasengeschwindigkeit also
r
ctief =
g
=
k
r
gλ
2π
(29)
Im Flachwasser geht h → 0, lim tanh(hk) = hk und die Phasengeschwindigkeit wird zu
h→0
cf lach
√
k gh p
=
= gh
k
(30)
Die Ausbreitungsgeschwindigkeit nimmt also mit abnehmender Tiefe ab, was erklärt, warum
Wellen in flachem Wasser gebeugt werden und als Konsequenz immer auf das Ufer zu laufen1.
Abbildung 1: Wellenfronten, die sich auf eine kreisförmige Insel zu bewegen (durchgezogene
Linien). Außerdem sind Höhenlinien unter Wasser eingezeichnet (gestrichelte Linien). Sobald
die Welle den Boden spürt“ verlangsamt sie sich, wodurch sie gebeugt wird und auch auf der
”
Rückseite der Insel noch auf das Ufer zu läuft [1]
Außerdem können wir aus dem Potential Informationen über das Geschwindigkeitsfeld der
Fluidteilchen gewinnen


v=

u(x, z, t)

 = 
0


w(x, z, t)
5
∂Φ
∂x
0
∂Φ
∂z





(31)
Schauen wir uns zuerst den Term
von ekz ergibt sich
cosh(k(z+h))
cosh(kh)
an. Durch Erweitern mit
e−kh
e−kh
−2k(z+h)
cosh(k(z + h))
ekz ekh + e−kz e−kh
kz 1 + e
=
=
e
cosh(kh)
ekh + ekh
1 + e−2kh
und Ausklammern
(32)
Im Tiefwasser, also für h → ∞, geht der ganze Term gegen ekz . Demnach gilt für das Potential
in tiefem Wasser
Φ(x, z, t) =
ag kz
aω kz
e cos(ωt − kx) =
e cos(ωt − kx)
ω
k
(33)
wobei in der zweiten Gleichung die Dispersionsrelation für tiefes Wasser, ω = gk
, verwendet
ω
wurde.
Damit ergibt sich für die Horizontal- und Vertikalkomponente der Teilchengeschwindigkeit
u(x, z, t) = aωekz sin(ωt − kx)
w(x, z, t) = aωekz cos(ωt − kx)
(34)
Die Fluid-“teilchen“ führen also eine Kreisbewegung (Orbitalbewegung) aus, deren Amplitude
mit der Tiefe exponentiell abnimmt 2
Abbildung 2: Fluid-“teilchen“ führen eine Orbitalbewegung aus, so dass sich das Wasser
am Wellenkamm in Richtung der Ausbreitungsgeschwindigkeit bewegt, im Wellental
entgegengesetzt. Mit zunehmender Tiefe werden die Orbitale exponentiell kleiner. [1]
6
2
Kapillarwellen [2] [3]
Im zweiten Abschnitt wollen wir uns Wasserwellen kleiner Wellenlängen anschauen. Die Motivation
für diesen Schritt ist, dass bei immer kleiner werdenden Wellenlängen nicht mehr die Schwere,
sondern die Oberflächenspannung die treibende Kraft für die Wellenausbreitung ist und sich
daher unsere Dispersionsrelation ändert.
Für die Untersuchung betrachten wir zunächst die Auswirkungen der Oberflächenspannung auf
die nun nicht mehr freie Oberfläche des Wassers.
Abbildung 3: Zylindrisch gekrümmte Oberfläche mit Oberflächenspannungen Σ und Σ0 . m steht
für die Auslenkung. Unten links ist noch das Kräftedreieck der Oberflächenspannungen mit ihrer
Resultante N ∆s zu sehen [2]
Wir nehmen zunächst die Oberfläche als zylindrisch an, da sich die Eigenschaften der
doppelt gekrümmten Oberfläche einfach ableiten lassen. In Abbildung 3 sieht man eine solche
Oberfläche. Dabei sind Σ und Σ0 vom Betrag her gleiche Oberflächenspannungen. Deren Resultante
drücken wir mit einer auf die Längeneinheit der Saite bezogenen Größe N aus. Aus dem
Kraftdreieck folgt dann
N · ∆s = Σ · ∆
(35)
Weiterhin kann man sich noch die Definition der Krümmung (herleitbar über den Anstiegswinkel
der Tangensfunktion [5]) anschauen
2
∂ m
1
∆
∂x2
= lim
=±
3
R ∆s→0 ∆s
(1 + ( ∂m )2 ) 2
(36)
∂x
Damit erhalten wir für kleine Auslenkungen m den einfachen Ausdruck
N=
1
∂ 2m
Σ=− 2Σ
R
∂x
7
(37)
Man sieht hier leicht, dass N zu einer Verminderung der Krümmung führt und auch, dass
37 die Differentialgleichung der schwingenden Saite liefert, wenn man N durch einen auf die
Längeneinheit bezogenen Trägheitswiderstand mit linearer Dichte ρ ersetzt.
ρ
∂ 2m
∂ 2m
=
Σ
∂t2
∂x2
(38)
Man beachte, dass in der Schwingungsgleichung für die örtliche Komponente eigentlich ein
Laplace-Operator verwendet wird, wir hier allerdings nur einen eindimensionalen Fall betrachtet
haben. Bei einer doppelt gekrümmten Oberfläche kann man unser bisherige Überlegungen
einfachen übertragen. Der Krümmungsradius wir lediglich durch die beiden Hauptkrümmungsradien
ersetzt und die Ausrichtung ihrer Schnitte als x- und y-Richtung angesehen. Daraus ergibt sich
allgemein:
∂ 2m
Σ ∂ 2m ∂ 2m
=
·( 2 +
)
∂t2
ρ
∂x
∂y 2
(39)
Zuletzt indentifizieren wir unser N noch mit dem Druck p.
Nun kommen wir zur eigentlichen Thematik, den ebenen Kapillarwellen und Kapillarschwerewellen.
Wie zuvor erwähnt ist unser Ziel das Ermitteln der zugehörigen Dispersionsrelationen. Wir
betrachten wieder eine zylindrisch gekrümmte Oberfläche und ersetzen die Auslenkung m durch
die Senkung −η. Wir betrachten hier die Bernoulli-Gleichung der Form
−
∂Φ 1
+ · (p + U ) = const.
∂t
ρ
(40)
wobei wir zunächst U = 0 setzen, da wir die Schwere erst später in unsere Betrachtungen
miteinbeziehen. Zusammen mit 37 ergibt sich dann
∂Φ Σ ∂ 2η
=
·
(41)
∂t z=0
ρ ∂x2
wobei wir stets nur die Oberfläche betrachten (daher z = 0). Das Geschwindigkeitspotential
Φ und Oberflächensenkung η haben nun den Charakter ebener Wellen und können daher
geschrieben werden als
Φ = A · ei(kx−ωt) · ekz
(42)
η = a · ei(kx−ωt)
(43)
Setzen wir nun 42 und 43 in 41 ein erhalten wir durch Aufhebung der Exponentialfunktionen
die Bedingung
Σ
iAω = k 2 a
ρ
Die oben bereits erwähnte kinematische Randbedingung lässt sich auch schreiben als
∂η
∂Φ =
∂t
∂z z=0
8
(44)
(45)
Daraus wiederum folgt die Bedingung
−iωa = kA
(46)
Wir können nun 45 und 46 zusammenfassen. Man kann bereits erkennen, dass hier bereits die
Dispersionsrelation enthalten ist, da wir eine Beziehung zwischen ω und k herstellen können.
A
Σ k2
−iω
=
=
a
ρ iω
k
(47)
Die daraus folgende Dispersionsrelation ist dann
ω2 =
Σ 3
k
ρ
(48)
Betrachtet man nun die Fortpfanzungsgeschwindigkeit c erkennen wir das Verhalten von Wasserwellen,
deren treibende Kraft lediglich die Oberflächenspannung ist
s
s
2
ω
Σ
Σ
Σ 2π
c2 = 2 = k; c =
k=
(49)
k
ρ
ρ
ρ λ
Abbildung 4: Ausbreitungsgeschwindigkeit c aufgetragen gegen λ. Die gestrichelten Kurven
sind jeweils die für Kapillarwellen ohne Schwere und Schwerewellen für tiefes Wasser. Die grüne
Kurve ist die daraus Resultierende. [2]
Man sieht, dass Kapillarwellen ein anderes Verhalten für Wellenlänge und Ausbreitungsgeschwindigkeit
mit sich bringen. Wir vergleichen hier nur Kapillarwellen mit tiefen Schwerewellen, da h/z und
hk bei kleinen Wellenlängen immer sehr groß sind. Kombiniert ergeben beide Dispersionsrelationen
eine anomale Dispersion, deren Konsequenz ist, dass es eine Wellenlänge mit minimaler Ausbreitungsgeschwindi
gibt.
Um nun den konkreten Fall von Wasser auf der Erde zu betrachten, können wir in die BernoulliGleichung 40 noch die Schwere U = ρgη einbringen. Gehen wir wieder gleich vor und bringen
die kinematische Randbedingung mit ein, bekommen wir hierfür die Dispersionsrelation
ω2 =
Σ 3
k + gk
ρ
9
(50)
Das Quadrat der Fortpflanzungsgeschwindigkeit ist dann
c2 =
ω2
Σ
g
=
k
+
k2
ρ
k
(51)
In Abbildung 4 interessiert uns nun konkret das Minimum von c bzw. c2 . Wir betrachten also
die Gleichung
2c
dc
d Σ
g dk
=
( k+ )
=0
dλ
dk ρ
k dλ
(52)
Durch der Ausdruck in der Klammer folgen also die Bedingungen
Σ
g
= 2
ρ
k
λmin
(53)
2π
=
= 2π
k
s
Σ
ρk
(54)
54 liefert auch eine Bedinung für k, die bei minimaler Ausbreitungsgeschwindigkeit gilt. Diese
setzen wir in 51 und bekommen
s
Σg
c2min = 2
(55)
ρ
Jetzt muss man lediglich die gegeben Werte einsetzen und erhält die minimale Ausbreitungsgeschwindigkeit
kg
von Wasserwellen, sowie deren Wellenlänge. Es gelten Σ = 72 · 10−3 kg
, ρ = 103 m
3 und
s2
m
g = 9, 81 s2 :
λmin = 0, 017m; cmin = 0, 23
m
s
(56)
Das bedeutet, dass es keine sich langsamer ausbreitenden Wellen im Wasser gibt, als solche mit
der Wellenlänge von 1, 7cm. Alles darüber hinaus oder darunter hat eine höhere Ausbreitungsgeschwindigkeit.
3
Mach’sches Phänomen [2]
Eine interessante Konsequenz der Schwerewellen im tiefen Wasser und ihrer Dispersionsrelation
ist, dass sie sich nicht an das Mach’sche Phänomen halten. Dringt ein Objekt in ein Medium
mit höherer Geschwindigkeit als dessen spezifische Schallgeschwindigkeit ein, bildet sich hinter
ihm eigentlich ein Mach’scher Kegel aus. Die hervorgerufenen Ringwellen formen diesen Kegel,
dessen Öffnungswinkel von der Geschwindigkeit des Objekt und der Schallgeschwindigkeit
abhängt.
sin(θ0 ) =
c
v
(57)
Dieser Effekt lässt sich bei einem Schiff, dass durch tiefes Wasser fährt allerdings nicht beobachten.
Schauen wir uns folgende Situation an:
10
Abbildung 5: Schiff fährt von Punkt Q zu O. Wir betrachten Senkung η bei P. [2]
Q ist der Aufenthaltspunkts des Schiffs zur Zeit t = −t0 und O der zum Zeitpunkt t = 0.
Wir untersuchen die Senkung der Wellen im Punkt P. Nach dem Kosinussatz gilt nun
rt2 = r2 + v 2 t02 − 2rv(−t0 )cosθ
(58)
Auf die weiteren Rechnungen gehen wir hier nicht genauer ein. Man kann sie im Sommerfeld [2]
einzeln nachlesen. Zusammengefasst integrieren wir am Punkt P über alle Senkungen ηt aller
vom Schiff ausgesendeten Ringwellen. Nun interessiert uns der Moment, an dem sich η zum
ersten Mal ändert. Mit der mathematischen Methode der stationären Phase erhalten wir dann
die Bedingung
r
2r2
t2 + 3 cos(θ)t + 2 = 0
v
v
Setzen wir dies in die P-Q-Formel erhalten wir als Bedingung für t
r
3r
8
t1,2 = − (cos(θ) ± cos2 (θ) − )
2v
3
(59)
(60)
Nun muss unser t nicht nur negativ sein, sondern auch reell, um einen physikalischen Sachverhalt
zu beschreiben. Dies wiederum bedeutet, dass durch die Wurzel θ an die Bedingung
cos2 θ >
8
9
(61)
geknüpft ist. Das hat zur Folge, dass es einen Grenzwinkel θ0 gibt, ab dem es keine Senkung
gibt. Dieser beträgt
θ0 = 19◦ 280
(62)
Das bedeutet, dass Bugwellen hinter einem Schiff, unabhängig von dessen Geschwindigkeit,
einen festegelegten Öffnungswinkel haben. Dies beruht auf der Dispersionsrelation, die zur Folge
hat, dass es immer eine Welle gibt, deren Ausbreitungsgeschwindigkeit gleich der Fahrtgeschwindigkeit
des Schiffes ist und mit ihm mitläuft. In seichtem Wasser fällt dieser Effekt wieder weg, da die
Wellengeschwindigkeit nur von der Wasserhöhe abhängt. Tatsächlich verhalten sich Bugwellen
im seichten Wasser entsprechend der Beschreibung des Mach’schen Phänomens.
11
Literatur
[1] B. Kinsman, Wind Waves, their generation and propagation on the ocean surface, PrenticeHall, Inc. 1965
[2] A. Sommerfeld: Mechanik der deformierbaren Medien. Verlag Harri Deutsch, Frankfurt
1978
[3] Landau-Lifschitz Band VI: Hydrodynamik, Akademie Verlag1990
[4] http://folk.ntnu.no/oivarn/hercules_ntnu/LWTcourse/lwt_new_2000_Part_A.pdf
[5] http://de.wikipedia.org/wiki/Kr%C3%BCmmung
12