Analysis: Differentialgleichungen

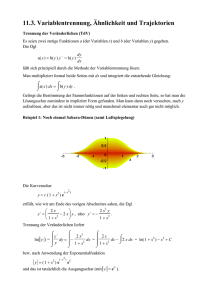
Analysis
Differentialgleichungen
Edward Lorenz (*1917 in West Haven, Connecticut) der Meteorologe. Er studierte Wettermodelle auf dem
Computer. Dabei stellte er fest, dass sehr kleine Änderungen in den Anfangsbedingungen grosse Wirkung
haben kann (Schmetterlingseffekt). Ihm gelang es, die darunterliegende Mathematik zu beschreiben. Es
handelt sich um drei gekoppelte Differentialgleichungen. Die Figur stellt eine Lösung dieser Gleichungen dar.
1. Lösen von Differentialgleichungen
Einleitung
Definition: Eine Differentialgleichung (oft durch DGL abgekürzt) ist eine Gleichung, in der eine
Funktion y(x) und deren Ableitungen auftreten. Gesucht ist die Funktion.
Wir haben gesehen, dass Differentialgleichungen in der Physik eine sehr wichtige Rolle spielen.
Auch in sehr vielen anderen Gebieten sind sie von grosser Bedeutung. Wir wollen deshalb ganz
allgemein solche Differentialgleichungen lösen. Dies ist im Allgemeinen sehr schwierig oder nicht
möglich. Es gibt jedoch einige wichtige Spezialfälle, die wir lösen können.
Überprüfen von vorgegebenen Lösungen
In einigen Fällen können die Lösungen bereits bekannt sein. Zum Beispiel ist aus Beobachtungen
und Messungen eine These über die Lösung aufgestellt wurde. Ob diese stimmt, kann
mathematisch überprüft werden.
In den folgenden Aufgaben sind die Differentialgleichungen und ihre Lösungen gegeben.
Überprüfe, ob diese Lösungen stimmen.
Lösung: y = x + Ce–x
mit C ∈ \
Lösung: y = Cx3 – x2
mit C ∈ \
1.1 DGL:
y‘ = x – y + 1
1.2 DGL:
y‘ =
1.3 DGL:
xy‘ + y = sin(x)
Lösung: y =
1
(C – cos(x))
x
mit C ∈ \
1.4 DGL:
y‘ = xy2 – y
Lösung: y =
1
1+ x + Ce x
mit C ∈ \
3y
+x
x
Wir definieren nun die Differentialgleichung mathematisch präzise:
Definition: Eine Differentialgleichung besteht aus einer Funktion F der gesuchten Funktion y(x) und
deren Ableitungen auf der einen Seite und einer Funktion f der Variable x auf der anderen
Seite.
§ dy d2 y d3 y
dn y ·
F ¨ y, , 2 , 3 ,..., n ¸ = f ( x )
dx ¹
© dx dx dx
Die Differentialgleichung hat den Grad n.
1.5 Handelt es sich wirklich in all diesen Aufgaben Differentialgleichungen gemäss dieser
Definition? Welchen Grad haben sie?
Analysis: Differentialgleichungen
Seite 2
www.mathema.ch (November 11)
Anfangsbedingungen
Die Lösungen aus Aufgabe 1.1 bis 1.4 enthalten jeweils noch eine Integrationskonstante C. Die
Lösung ist also nicht eindeutig. Mehrere Funktionen y(x) erfüllen die gegebene Differentialgleichung. Die Integrationskonstante C wird durch die Anfangsbedingungen festgelegt. Es muss
also zusätzlich noch bekannt sein, welcher Wert die Funktion für ein bestimmtes Argument
annimmt.
Bestimme die Lösung der obenstehenden vier Differentialgleichungen bei bekannter
Anfangsbedingung:
2.1 DGL:
y‘ = x – y + 1
2.2 DGL:
y‘ =
2.3 DGL:
xy‘ + y = sin(x)
mit der Anfangsbedingung y(π) = 0
2.4 DGL:
y‘ = xy2 – y
mit der Anfangsbedingung y(0) =
3y
+x
x
mit der Anfangsbedingung y(0) = 5
mit der Anfangsbedingung y(1) = 9
1
3
Satz: Hat eine Differentialgleichung den Grad n, so hat ihre allgemeine Lösung n
Integrationskonstanten. Um die Funktion eindeutig festzulegen, müssen also n
Anfangsbedingungen gegeben sein.
2.5 Gegeben ist die Differentialgleichung y‘ = (y – 2)2.
1
eine Lösung der
x+3
obigen Differentialgleichung für die Anfangsbedingung f(–4) = 3 ist.
Es soll gezeigt werden, dass die Funktion y = 2 –
2.6 Gegeben ist die Differentialgleichung (1 + x2)⋅y‘ + x⋅y = 0 mit der Anfangsbedingung
y(1) =
2 beschrieben.
Es soll gezeigt werden, dass Funktion y =
2
1+ x 2
eine Lösung der obigen
Differentialgleichung ist.
Analysis: Differentialgleichungen
Seite 3
www.mathema.ch (November 11)
Lineare, homogene Differentialgleichungen
Ein sehr wichtiger Typ von Differentialgleichungen sind die linearen Differentialgleichungen. Die
wichtigsten Bewegungsgleichungen sind lineare Differentialgleichungen.
Definition: Eine Differentialgleichung heisst linear, falls die Funktion F lineare in der gesuchten
Funktion y(x) und deren Ableitungen ist:
n
¦ ai
i=0
di y
= f (x)
dx i
mit den Koeffizienten ai ∈ \
anderenfalls heisst sie nicht-linear.
Wirkt zusätzlich keine äussere Kraft auf das System, so ist die Gleichung homogen.
Definition: Eine lineare Differentialgleichung heisst zusätzlich homogen, falls f(x) = 0, also
n
¦ ai
i=0
di y
=0
dx i
sonst heisst sie inhomogen.
3.1 Welche der DGLs in 1.1 bis 1.4 sind linear, welche linear und homogen?
3.2 Erfinde zwei bis drei Beispiele für eine lineare, homogene Differentialgleichung.
Lineare, homogene Differentialgleichungen können wir durch Tüfteln lösen. Du musst also eine
Funktion suchen, die die Gleichung erfüllt. Denk daran, du musst die allgemeinste Lösung mit der
entsprechenden Anzahl Integrationskonstanten finden.
3.3 y’ – y = 0
3.4 y’ + y = 0
3.5 y‘‘ + y = 0
3.6 y‘‘ + y‘ + y = 0
3.7 y‘‘ + 2λy‘ + ω02y = 0
Analysis: Differentialgleichungen
mit λ, ω = konst.
Seite 4
www.mathema.ch (November 11)
Separation der Variablen
Eines der bekanntesten Verfahren zum expliziten Lösen ist das sogenannte Lösen durch Trennung
der Variablen. Dieses Verfahren funktioniert allerdings nur dann, wenn sich die Differentialgleichung erster Ordnung in der Form y‘ =g(y)·f(x) schreiben lässt.
Beispiel
dy
dx
y′ = y 2 ⋅ x
mit y′ =
dy
= y2 ⋅ x
dx
: y2
1 dy
⋅
=x
y 2 dx
⋅ dx
1
⋅ dy = x ⋅ dx
y2
Integration beider Seiten
1
³y
2
⋅ dy = ³ x ⋅ dx
Ausführen des Integrals 1
1
1
− + C1 = x 2 + C2
2
y
− C1
1 1
− = x 2 + C2 − C1
y 2
C := C2 − C1
1 1
− = x2 + C
y 2
⋅ ( −1)
1
x2 + 2 ⋅ C
1
= − x2 − C = −
2
y
2
Auflösen nach y
y=−
2
x + 2⋅C
mit C ∈ \
2
Löse die folgenden Differentialgleichungen durch Trennung der Variablen:
4.1 DGL: y‘ = y2
4.2
DGL: y‘ = –x·y
x
y
4.4
DGL: y‘ =
4.3 DGL: y‘ =
4.5 DGL:
1
y
x
y·y‘ – x = 0 mit der Anfangsbedingung y(1) = 0
Das Integral sucht eine Funktion F(x), die abgeleitet die gegebene Funktion f(x) ergibt, also F‘(x) = f(x).
³ f ( x ) dx = F ( x )
⇔ F′ ( x ) = f ( x )
Analysis: Differentialgleichungen
Seite 5
www.mathema.ch (November 11)
2. Das Eulerverfahren
Einleitung
Wir haben ein Verfahren zum exakten Lösen von
Differentialgleichungen, das Verfahren durch
Separation der Variablen, kennengelernt. Es gibt
viele weitere solcher Verfahren, um Differentialgleichungen exakt zu lösen. Sie lassen sich jedoch
leider nur bei den wenigsten Differentialgleichungen anwenden. Deswegen brauchen wir
Verfahren, um auch für solche Differentialgleichungen Lösungen zu finden, für die sich
keine exakte Lösung finden lässt. Es lässt sich dann
nicht eine explizite Lösung in Form von
einer Funktionsvorschrift angeben, sondern nur
näherungsweise die numerischen Funktionswerte.
Eines der einfachsten solcher numerischer
Lösungsverfahren hierfür ist das Eulerverfahren.
Was macht das Eulerverfahren?
Leonhard Euler (*1707 in Basel; †1783 in Petersburg)
war einer der bedeutendsten Mathematiker.
Durch die die Differentialgleichung y‘ = g(y, t) ist die Steigung von y im Punkt P(t|y) gegeben. Wir
beginnen beim Anfangswert y(t0) = y0 und berechnen die Steigung in diesem Punkt. Wir bewegen
uns nun um einen Schritt der Breite Δt entlang der horizontalen Achse. Den neuen Funktionswert
y(t) schätzen wir, indem wir annehmen, dass sich die Funktion mit der Steigung y‘ linear fortsetzt.
Ein Beispiel
Wir wollen die Differentialgleichung y‘ = –0.5·y
unter der Anfangsbedingung y(0) = 100 mit dem
Eulerverfahren lösen. Wir wollen die Funktionswerte
im Intervall [0, 10] näherungsweise berechnen.
Dazu teilen wir das Intervall in zehn Teile mit der
Breite Δt = 1 ein.
t
y
Δt
0
100
1
Δy
1
1
1
1.1 Fülle die fehlenden Werte in der
nebenstehenden Tabelle aus.
1.2 Auf der nächsten Seite ist ein Diagramm
vorbereitet. Beschrifte die Achsen und
zeichne die Punkte ein.
Analysis: Differentialgleichungen
Seite 6
www.mathema.ch (November 11)
100
90
80
70
60
50
40
30
20
10
0
0
1
2
3
4
5
6
7
8
1.3 Löse die Differentialgleichung exakt, berechne zehn Funktionswerte
(Tabelle) und zeichne auch diese Punkte im Diagramm ein.
1.4 Der Taschenrechner kennt das Eulerverfahren. Finde mit der Anleitung
zum Rechner heraus, wie das funktioniert. Berechne und zeichne nun
die Näherung mit dem Eulerverfahren für die Differentialgleichung
y‘ = 0.5·y unter der Anfangsbedingung y(0) = 100.
1.5 Wir wollen nun das Intervall [0, 10] in immer mehr Schritte aufteilen.
Zeichne und berechne nun die Näherung mit dem Eulerverfahren für
20, 100 und 1000 Schritte. Wie verhalten sich die Näherungen mit
zunehmender Anzahl Schritte?
9
10
t
y
0
100
1
2
3
4
Aufgaben
2.1 Gegeben ist die Differentialgleichung y‘ = t2 – 3t mit der
Anfangsbedingung y(0) = 2.
Wie lautet die explizite Lösung dieser Differentialgleichung?
Berechne mittels des Eulerverfahrens und der Schrittweite
Δt = 0.5 näherungsweise den Funktionswert f(1) und vergleiche
den Näherungswert mit dem exakten Wert von f(1).
2.2 Gegeben ist die Differentialgleichung y‘ = y2 + y mit der Startbedingung y(0) = 1. Löse die
Gleichung mit dem Eulerverfahren. Wähle die Schrittweite Δt = 0.5. Berechne einen
Näherungswert für y(2).
Analysis: Differentialgleichungen
Seite 7
www.mathema.ch (November 11)
3. Graphische Darstellung
y(t)
Richtungsfelder
Differentialgleichungen erster Ordnung
y‘(t) = g(y, t) können durch ihr Richtungsfeld
graphisch dargestellt werden:
In jedem Punkt P(t|y) des Koordinatensystems ist
durch die Differentialgleichung y‘ = g(y, t) die
Steigung von y gegeben und sie kann somit
berechnet werden.
Im Koordinatensystem vermerkt man die Steigung
im Punkt P(t|y) mit einem kurzen Strich durch den
Punkt P mit der entsprechenden Steigung. Dies
macht man in vielen Punkten und erhält so einen
Eindruck des Richtungsfeldes der vorliegenden
Differentialgleichung.
t
Figur 1: Richtungsfeld der DGL y‘ = y
In Figur 1 ist als Beispiel das Richtungsfeld der
Differentialgleichung y‘ = y abgebildet.
Das Richtungsfeld gibt eine grobe Vorstellung von
den möglichen Lösungen. Jeder Graph, der sich
‚stimmig‘ in das Richtungsfeld einzeichnen lässt,
entspricht dem Graphen einer möglichen
Lösungsfunktion der Differentialgleichung. Mit
‚stimmig‘ ist gemeint, dass die Steigung des
Graphen mit der Steigung des Richtungsfeldes der
Differentialgleichung an jeder Stelle übereinstimmt.
Figur 2: Richtungsfeld mit ‚stimmigen‘ und mit ‚nicht
stimmigen? Graphen. der DGL y‘ = y
In Figur 2 siehst du einen mit dem Richtungsfeld
einer Differentialgleichung ‚stimmigen‘ Graphen
(Exponentialfunktion) und einen ‚nicht stimmigen‘
(Polynom dritten Grades).
Zu einem Richtungsfeld gibt es jedoch unendlich
viele Lösungen, d.h. Graphen, die sich ‚stimmig‘ in
das Richtungsfeld einpassen lassen (vgl. Figur 3).
Ist der Anfangswert bekannt, d.h. man kennt den
Funktionswert an einer bestimmten Stelle y(t0) = y0,
so ist die Lösung eindeutig bestimmt. Weiss man
beim Beispiel in Figur 3 zusätzlich, das gilt
y(0) = 1, so kommt als Lösung nur noch der
oberste in der Figur gezeichnete Graph in Frage.
Analysis: Differentialgleichungen
Seite 8
Figur 3: Zu einem Richtungsfeld gibt es unendlich viele
‚stimmige‘ Graphen.
www.mathema.ch (November 11)
Übungen 1
ƒ Zeichne bei Aufgabe 1.1 bis 1.3 das Richtungsfeld von Hand.
ƒ Diskutiert untereinander, wie eine mögliche Lösungskurve aussehen könnte. Zeichnet sie
nach Augenmass ein.
1.1 y‘ = t
1.2 y‘ t = 1
1.3 y‘ = y
ƒ Studiere danach die Unterlagen zum TI-89, in welchen Dir erklärt wird, wie man ein
Richtungsfeld auf dem Rechner darstellen kann.
ƒ Diskutiert untereinander, wie eine mögliche Lösungskurve aussehen könnte. Zeichnet sie nach
Augenmass ein. Zeichne allenfalls auch die Funktion auf dem Rechner.
1.4 y‘ =
1
y +1
2
1.5 y‘ = t – y
1.6 yy‘ + t = 0
1.7 y‘ = et – y
Übungen 2
2.1 Findest Du zu den Aufgaben 1.1 bis 1.3 die explizite Lösung? Gesucht ist also die
Funktionsvorschrift y(t) = … Denke auch an die Integrationskonstante.
2.2 Löse die folgenden Differentialgleichungen (vgl 1.1 bis 1.3) unter den gegebenen
Anfangsbedingungen:
y‘ = t
mit y(0) = –2
y‘ t = 1
mit y(1) = 1
y‘ = y
mit y(0) = 0.5
Zeichne die gefundenen Lösungen in die entsprechenden Richtungsfelder ein, die du bei der
Aufgabe 1 gefunden hast.
Analysis: Differentialgleichungen
Seite 9
www.mathema.ch (November 11)
4. Anwendungen
1.
Der Innenraum eines Backofens hat die Temperatur T = 250°C. Die Raumtemperatur beträgt
20°C. Der Ofen wird nun ausgeschaltete und beginnt sich abzukühlen. Die Temperatur im
Ofen ist also eine Funktion der Zeit T(t). Die Änderung der Temperatur T‘(x) ist proportional
zur Temperaturdifferenz zwischen Innenraum und der Umgebung. Diese Differentialgleichung
drückt dies aus:
T′ ( t ) = −0.02 ª¬ T ( t ) − 20 º¼ .
Überlege dir, weshalb diese Gleichung eine sinnvolle Beschreibung des Prozesses ist.
Berechne die Funktion T(t). Wie lange dauert es bis, der Ofen sich auf 135°C abgekühlt hat?
2.
Das Wachstum einer Taufliegen-Population unter Laborbedingungen kann näherungsweise
durch die Differentialgleichung
N‘(t) = 0.0006 N(t) Ã [350 ï N(t)]
beschrieben werden. N(t) bezeichnet die Anzahl Taufliegen zur Zeit t in Tagen.
a. In einigen ausformulierten Sätzen soll erläutert werden, warum diese Differentialgleichung
eine sinnvoll Beschreibung einer Taufliegen-Population darstellt.
b. Wie sieht das Richtungsfeld der Differentialgleichung in einem relevanten Bereich aus?
c. Nach wie vielen Tagen hat sich eine zu Beginn 100 Taufliegen umfassende Population
verdoppelt?
d. Es soll gezeigt werden, dass die Funktion
350
N(t ) =
1+ 13 ⋅ e−0.21t
eine Lösung der Differentialgleichung ist.
e. Wie sieht die Wachstumskurve N(t) aus? Welche Koordinaten hat der Wendepunkt?
3.
Der Durchmesser d(t) einer Fichte auf ein Meter Höhe über dem Boden in Abhängigkeit des
Alters t in Jahren wird näherungsweise beschrieben durch die Differentialgleichung
d‘(t) = 0.05 d(t) Ã [1 ï d(t)]
a. Berechne eine Näherung der Lösung mit dem Eulerverfahren. Wir wissen, dass eine 60jährige Fichte einen Durchmesser von 0.5 Meter hat.
b. Es soll überprüft werden, dass die Funktion
1
d(t) =
−0.05t + 3
1+ e
eine Lösung der Differentialgleichung ist.
c. Gesucht ist eine Skizze des Graphen der Wachstumsfunktion in einem relevanten Bereich.
Analysis: Differentialgleichungen
Seite 10
www.mathema.ch (November 11)
3.
Versenken von Atommüll im Meer!
Über Jahre hinweg wurde radioaktives Material eingeschlossen in Fässern im Meer versenkt,
typischerweise in Regionen, wo die Meerestiefe rund 100m beträgt. Von Interesse war dabei
unter anderem die Aufprallgeschwindigkeit der Fässer auf dem Meeresboden. Eine
Aufprallgeschwindigkeit von 20m/s und mehr galt für die verwendeten Fässer als höchst
kritisch. Die Messung der Aufprallgeschwindigkeit ist technisch nicht ganz einfach. Hingegen
lässt sich das Absinken der Fässer mittels eines einfachen physikalischen Modells ohne
Probleme simulieren.
a. Welche Kräfte wirken auf das Fass?
b. Stelle die Bewegungsgleichung für das Fass auf.
c. Unter Berücksichtigung fässerspezifischer Parameter finden wir folgende
Bewegungsgleichung:
s‘‘(t) = 3.477 – 0.015982s‘
Hat diese Bewegungsgleichung wirklich dieselbe Form, wie die von dir bei b. gefundene
Bewegungsgleichung?
d. Die Gleichung ist zweiten Grades. Wir interessieren uns jedoch nur für die
Geschwindigkeit. Kannst Du die Gleichung als Differentialgleichung für v darstellen?
e. Die Fässer werden zur Zeit t = 0 mit der Anfangsgeschwindigkeit v(0) = 0 versenkt. Löse
die Gleichung mit dem Eulerverfahren. Schwierig: Findest Du auch eine explizite Lösung?
f. Ist das Versenken der Fässer vom Standpunkt des Berstens aufgrund dieser
Modellannahmen kritisch oder nicht?
4.
Ein Federpendel wird zur Zeit t = 0 aus der Position y = 10 cm losgelassen. Das Pendel
schwingt frei, die Pendelmasse ist m = 100 g und die Federkonstante beträgt k = 5 N/m.
Berechne den Ort des Pendels zur Zeit t = 120 s.
5.
Approximation der Zahl e
Gegeben ist die Differentialgleichung y‘ = y mit der Anfangsbedingung y(0) = 1. Diese
Differentialgleichung hat die Lösung y = et . Insbesondere erhält man also für den
Funktionswert y(1) = e. Löst man die Differentialgleichung ausgehend vom Startwert mit dem
Eulerverfahren numerisch, lässt sich also die Eulerzahl approximieren. Welchen Näherungswert für e liefert das Eulerverfahren bei Schrittweite ;t = 0.1 bzw. bei Schrittweite Δt = 0.01?
Analysis: Differentialgleichungen
Seite 11
www.mathema.ch (November 11)
5. Bewegungsgleichungen
Differentialgleichungen
Sir Isaac Newton2 suchte nach Möglichkeiten Bewegungen
mathematisch zu erfassen. Dazu entwickelte er die
Differentialrechnung (zeitgleich mit Gottfried Wilhelm Leibniz3).
Der Begriff der Ableitung vereinfachte die Beschreibungen und
Berechnung von Geschwindigkeit und Beschleunigung
wesentlich einfacher. Die grosse Leistung bestand jedoch in
einem neuen Typ Gleichung – der Differentialgleichungen.
Mithilfe von Differentialgleichungen lassen sich unter anderem
physikalische Systeme beschreiben und deren Bewegung unter
dem Einfluss von äusseren Kräften berechnen. Newton ist es so
gelungen Systeme mit gleichförmiger Bewegung bis hin zu den
Planeten auf ihren Bahnen, zu beschreiben.
Definition: Eine Differentialgleichung (oft durch DGL abgekürzt) ist eine Gleichung, in der eine
Funktion und deren Ableitungen auftreten. Gesucht ist die Funktion.
Wir werden ganz allgemein Differentialgleichungen studieren. Als Einstieg betrachten wir jedoch,
genauso wie Newton, Bewegungsgleichungen. Wir werden daran einige allgemeine Eigenschaften
von Differentialgleichungen kennenlernen. Einige Gesetze aus der Physik werden dir bekannt
vorkommen und du wirst besser verstehen, woher sie rühren.
Die Bewegungsgleichung
Ort, Geschwindigkeit und Beschleunigung
Wir betrachten einen bewegten Körper. Sein Ort x ändert sich also als Funktion der Zeit. Im
Allgemeinen ändern sich auch seine Geschwindigkeit v und seine Beschleunigung a mit der Zeit.
Wir definieren diese Grössen also wie folgt:
Ort
x = x (t)
Geschwindigkeit
v = v (t) =
dx
= x
dt
Beschleunigung
a = a(t) =
dv d2 x
=
= x
dt dt 2
Bemerkung: Newton notiert die Ableitungen nach der Zeit sehr kompakt mit einem kleinen Punkt.
Für die Ableitung des Weges nach der Zeit, der Geschwindigkeit, notiert er also sehr kurz x .
Die zweie Ableitung wird durch zwei Punkte angegeben x (Beschleunigung).
2
3
Sir Isaac Newton: *1643 in Woolsthorpe-by-Colsterworth in Lincolnshire; †1727 in Kensington, London
Gottfried Wilhelm Freiherr von Leibniz: *1646 in Leipzig; †1716 in Hannover
Analysis: Differentialgleichungen
Seite 12
www.mathema.ch (November 11)
Bewegungsgleichung
Du hast in der Physik die Gleichung F = mÃa kennengelernt. Vermutlich ist dies für dich die
Definition der Kraft. Die Aussage dieser Gleichung geht jedoch wesentlich weiter. Es handelt sich
dabei um die Bewegungsgleichung eines Körpers mit der Masse m unter dem Einfluss der
resultierenden Kraft F. Schreiben wir anstelle von a die zweite Ableitung des Ortes x , so erhalten
wir eine Differentialgleichung:
m ⋅ x = F
Gesucht wird also der Ort x als Funktion der Zeit.
Diese Gleichung kann einfach, aber auch sehr kompliziert sein. Die resultierende Kraft F kann
selber wieder Funktion der Zeit oder des Ortes oder Geschwindigkeit sein. Wir studieren zuerst die
grundlegenden Bewegungstypen.
Physikalische Systeme
Die zwei grundlegenden Bewegungstypen
Das freie Masseteilchen
Die resultierende Kraft auf das Teilchen ist Null. Das freie Masseteilchen ist also die einfachste
physikalische Situation.
a)
Stelle die Bewegungsgleichung auf und löse sie.
b)
Ist die gefundene Lösung für die Funktion x(t) eindeutig? Was ist die physikalische Bedeutung
der Parameter im Ort-Zeit-Gesetz x(t)?
c)
Um welchen Bewegungstypen handelt es sich hier? Wo kommt er vor?
d)
Löse das Problem, falls sich das Teilchen zur Zeit t = 0 am Ort x0 = 5 m befindet und sich mit
der Geschwindigkeit v0 = 10 m/s bewegt. Ist das Problem nun eindeutig?
Eine konstante Kraft F
Auf ein Teilchen mit der Masse m wirkt die konstante Kraft F.
a)
Stelle die Bewegungsgleichung auf und löse sie.
b)
Ist die gefundene Lösung für die Funktion x(t) eindeutig? Was ist die physikalische Bedeutung
der Parameter im Ort-Zeit-Gesetz x(t)?
c)
Um welchen Bewegungstypen handelt es sich hier? Wo kommt er vor?
d)
Löse das Problem, falls sich das Teilchen zur Zeit t = 0 am Ort x0 = 5 m befindet und sich mit
der Geschwindigkeit v0 = 10 m/s bewegt. Ist das Problem nun eindeutig?
Bemerkung: In den Gleichungen, die du hier gelöst hast, kommt jeweils die zweite Ableitung des
Ortes x vor. Du findest jeweils auch zwei Integrationskonstanten. Diese Konstanten werden
durch die Anfangsbedingungen festgelegt.
Analysis: Differentialgleichungen
Seite 13
www.mathema.ch (November 11)
Die grundlegenden Kräfte
Untersuche die folgenden Systeme jeweils auf ihre Eigenschaften. Beantworte jeweils die folgenden
Fragen:
a)
Stelle die Bewegungsgleichung auf und löse sie.
b)
Was ist die physikalische Bedeutung der Integrationskonstanten im Ort-Zeit-Gesetz s(t)?
c)
Um welchen Bewegungstypen handelt es sich hier? Wo kommt er vor?
Die Federkraft
Ein Teilchen mit der Masse m hängt an einer Feder mit der Federkonstanten k. Wie bewegt sich
der Körper, wenn nur diese Kraft auf ihn wirkt? Wie bewegt sich der Körper, wenn nur diese Kraft
auf ihn wirkt?
Laminare Strömung: Stokes-Reibung
Der Strömungswiderstand auf einen Körper ist in gewissen Fällen in guter Näherung proportional
zu Geschwindigkeit des Körpers. Wie bewegt sich der Körper, wenn nur diese Kraft auf ihn wirkt?
Turbulente Strömung: Newton-Reibung
Ist die Strömung jedoch turbulent, so ist der Strömungswiderstand jedoch proportional zur
Geschwindigkeit im Quadrat. Wie bewegt sich der Körper, wenn nur diese Kraft auf ihn wirkt?
Instabiles System
Stellen wir uns eine Art umgekehrte Feder vor: Die Kraft ist proportional zur Auslenkung, jedoch
nicht der Auslenkung entgegen gerichtet sondern sie zeigt in dieselbe Richtung wie die Auslenkung.
Ist ein solches System physikalisch sinnvoll? Wie bewegt sich der Körper, wenn nur diese Kraft auf
ihn wirkt?
Komplexe Systeme
Federkraft und Reibung
Eine Masse m hängt an einer Feder mit der Federkonstanten k. Der Körper ist der Stokes-Reibung
unterworfen. Wie bewegt sich dieser Körper?
Fallbewegung mit Reibung
Eine Kugel mit Masse m fällt ins Wasser und sinkt. Auf diese Kugel wirken die Gewichtskraft, der
Auftrieb und die Stokes-Reibung. Beschreibe die Bewegung dieser Kugel.
Fallbewegung
Fällt ein Körper aus sehr grosser Höhe herunter, so ist die Gewichtskraft, die auf ihn wirkt nicht
konstant, sondern wird durch das Gravitationsgesetz beschrieben. Wie fällt dieser Körper?
Analysis: Differentialgleichungen
Seite 14
www.mathema.ch (November 11)
Typen von Differentialgleichungen
Wir definieren nun die Differentialgleichung und einige ihrer Eigenschaften:
Definition: Eine Differentialgleichung besteht einer Funktion F der gesuchten Funktion x und deren
Ableitungen auf der einen Seite und einer Funktion f der Variable t auf der anderen Seite.
§ dx d2 x d3 x
dn x ·
F ¨ x, , 2 , 3 ,..., n ¸ = f ( t )
dt ¹
© dt dt dt
Die DGL hat den Grad n.
Definition: Eine Differentialgleichung heisst homogen, falls f(t) = 0, also
§ dx d2 x d3 x
dn x ·
F ¨ x, , 2 , 3 ,..., n ¸ = 0
dt ¹
© dt dt dt
sonst heisst sie inhomogen.
Definition: Eine Differentialgleichung heisst linear, falls die Funktion F lineare in der gesuchten
Funktion x(t) und deren Ableitungen ist:
n
¦ ai
i= 0
di x
= f (t)
dt i
mit den Koeffizienten ai ∈ \
anderenfalls heisst sie nicht-linear.
Jedes dieser neuen physikalischen Systeme wird durch eine Bewegungsgleichung beschrieben. Es
handelt sich um neun verschiedene Differentialgleichungen. Stelle diese Gleichungen übersichtlich
zusammen.
ƒ Handelt es sich wirklich in allen Fällen um DGL gemäss der obenstehenden Definition?
ƒ Gib jeweils an welcher Grad die DGL hat.
ƒ Gib auch an, ob die DGL homogen oder inhomogen ist und ob linear oder nicht-linear ist.
Welche dieser DGL konntest Du lösen? Welche nicht?
Analysis: Differentialgleichungen
Seite 15
www.mathema.ch (November 11)