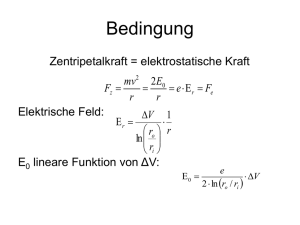
Quantenmechanik II Gelesen von Prof. Dr. Wolfram Weise im WS

Quantenmechanik II
Gelesen von Prof. Dr. Wolfram Weise
im WS 2010/11
Übungsaufgaben von Dr. Bertram Klein
In LATEX gesetzt von Tobias Ried
E-mail address: [email protected]
Literatur
zu I-III: L. D. Landau, E. M. Lifschitz: Theoretische Physik III (Quantenmechanik)
F. Schwabl: Quantenmechanik für Fortgeschrittene
zu IV: J. D. Bjorken, S. D. Drell: Relativistische Quantenmechanik
H. A. Bethe, R. Jackiw: Intermediate Quantum Mechanics
weiterführend: C. Itzykson, J. B. Zuber: Quantum Field Theory
iii
Inhaltsverzeichnis
Literatur
iii
Teil 1. Quantenmechanik zeitabhängiger Prozesse
Kapitel 1.
§1.1.
§1.2.
Rückblick und Vorbereitung
3
Axiome der Quantenmechanik
3
Zeitentwicklungsoperator; Schrödinger- und HeisenbergBild
4
Wiederholungsfragen
Kapitel 2.
Zeitabhängige Störungstheorie
§2.1.
Wechselwirkungsbild und Störungsentwicklung
5
9
9
§2.2. Übergänge erster Ordnung in einem diskreten Spektrum
10
§2.3.
Beispiel: zeitlich konstante Störung, die bei t = t0 eingeschaltet
wird
11
§2.4.
Zeitlich periodische Störungen, Fermis Goldene Regel
12
§2.5.
Elektromagnetische Übergänge
14
§2.6.
Elektrische Dipolübergänge
15
§2.7.
Ergänzung zur Wechselwirkung geladener Teilchen mit dem
elektromagnetischen Strahlungsfeld
16
Übungsaufgaben zu Kapitel 2
18
Teil 2. Elemente der quantenmechanischen Streutheorie
Kapitel 3.
§3.1.
Streuung
Streuprozess und Wirkungsquerschnitt
25
25
v
vi
Inhaltsverzeichnis
§3.2.
Nichtrelativistische Potentialstreuung
26
§3.3.
Stationäre Streuwellenfunktion
27
§3.4.
Streuung von Wellenpaketen
28
§3.5.
Differentieller Wirkungsquerschnitt dσ/dΩ
29
§3.6. Schrödinger-Gleichung als Integralgleichung, Greensche
Funktionen
§3.7. Bornsche Näherung
30
32
§3.8.
Beispiel: abgeschirmtes Coulomb-Potential/YukawaPotential
33
§3.9.
Die Partialwellenmethode
34
§3.10.
Das optische Theorem
40
§3.11.
Resonanzen
41
§3.12.
Inelastische Streuung
42
§3.13.
Operator-Formalismus der Streutheorie
42
Übungsaufgaben zu Kapitel 3
44
Teil 1
Quantenmechanik
zeitabhängiger
Prozesse
Kapitel 1
Rückblick und
Vorbereitung
1.1. Axiome der Quantenmechanik
(i) Der quantenmechanische Zustand eines Systems wird beschrieben
durch einen Zustandsvektor |ψi. |ψi ist Element eines HilbertRaums H.
(ii) Beobachtbare physikalische Größen (Observablen) werden dargestellt durch (hermitesche) Operatoren A auf H.
(iii) Die Zeitentwicklung eines Zustandes wird bestimmt durch die
zeitabhängige Schrödinger-Gleichung
(1.1)
∂
|ψ(t)i = H|ψ(t)i
∂t
mit Hamilton-Operator H.
i~
Bemerkungen.
(i) Die Zustände |ni seien Eigenzustände von A mit Eigenwerten an :
A|ni = an |ni. {|ni} bildet ein vollständiges Orthonormalsystem in
H mit hm|ni = δmn . Befindet sichP
ein System in einem Zustand
|ψi, so gilt die Entwicklung |ψi = n cn |ni mit cn = hn|ψi. |cn |2
gibt die Wahrscheinlichkeit
an, den Zustand |ψi im Eigenzustand
P
|ni zu finden. Es P
gilt n |cn |2 = 1, hψ|ψi = 1. Insbesondere gilt:
hAi = hψ|A|ψi = n |cn |2 an .
(ii) Es seien |φn i Eigenzustände des Hamilton-Operators:
H|φn i = En |φn i
3
4
1. Rückblick und Vorbereitung
Für einen beliebigen Zustand |ψ(t)i gilt
X
cn (t)|φn i
|ψ(t)i =
n
∂
Mit i~ ∂t
|ψ(t)i = H|ψ(t)i folgt sofort
i
cn (t) = hφn |ψ(t)i = e− ~ En t cn (0)
(iii) Für einen stationären Zustand mit Energie E gilt
i
|ψE (t)i = e− ~ Et |ψE (t = 0)i
∂
i~ ∂t
|ψE (t)i = H|ψE (t)i = E|ψE (t)i
Dies führt zur zeitunabhängigen Schrödinger-Gleichung
H|ψe i = E|ψE i,
|ψE i = |ψE (t = 0)i
(iv) Wellenfunktionen sind “Projektionen” von Zuständen |ψi in den
Ortsraum.
Es sei r̂ der Ortsoperator: Eigenzustände |ri (r̂|ri = r|ri), hr 0 |ri =
δ 3 (r − r 0 )
Wellenfunktion ψ(r, t) = hr|ψ(t)i
1.2. Zeitentwicklungsoperator; Schrödinger- und
Heisenberg-Bild
Die formale Lösung der Schrödinger-Gleichung
i~
∂
|ψ(t)i = H|ψ(t)i
∂t
ist
|ψ(t)i = U (t)|ψ(t = 0)i
mit
∞
(1.2)
U (t) = e
− ~i Ht
X (−i)ν
i
1
= 1 − Ht − 2 H 2 t2 + · · · =
~
2~
ν!
ν=0
Ht
~
ν
Der Zeitentwicklungsoperator U (t) ist unitär: U † (t) = U −1 (t). Bisher
(QMI) wurde in der Schrödinger-Darstellung (S-Bild) gearbeitet. Dort
sind die Zustände zeitabhängig und Operatoren (z.B. Ort r̂, Impuls p̂, Drehimpuls L̂,. . . ) zeitunabhängig.
Eine äquivalente Darstellung der Quantenmechanik verwendet das Heisenberg-Bild (H-Bild). Zustandsvektoren |ψH i = |ψ(t = 0)i sind zeitunabhängig, Operatoren AH = U † (t)AU (t) zeitabhängig.
5
Wiederholungsfragen
Erwartungswerte von Operatoren (Observablen) sind invariant unter
Wechsel der Darstellung (S-Bild ↔ H-Bild):
i
i
− ~ Ht
hψ(t)|A|ψ(t)i = hψH | e| ~ Ht Ae
{z
} |ψH i = hψH |AH |ψH i
AH
Satz 1.1 (Bewegungsgleichung für Operatoren). Für einen Operator A (im
S-Bild), der nicht explizit von der Zeit abhängt, gilt
i
i
d
(1.3)
AH (t) = [H, AH (t)] = (HAH (t) − AH (t)H)
dt
~
~
Man nennt diese Gleichung Heisenbergsche Bewegungsgleichung.
Beweis.
i
i
i
i
i
d
d h i Ht − i Ht i
=
AH (t) =
e ~ Ae ~
He ~ Ht Ae− ~ Ht − e ~ Ht Ae− ~ Ht H
dt
dt
~
i
= [H, AH (t)]
~
Bemerkung. Falls A(t) explizit zeitabhängig ist, muss man in 1.3 noch
∂
einen zusätzlichen Term ∂t
A(t) berücksichtigen.
Aus der Bewegungsgleichung liest man auch sofort ab:
Satz 1.2 (Erhaltungsgrößen). Observablen A bzw. AH , welche mit dem
Hamilton-Operator H kommutieren
(1.4)
[H, AH ] = [H, A] = 0
heißen Erhaltungsgrößen.
Wiederholungsfragen
(1) Was ist der Hamiltonoperator eines quantenmechanischen Systems?
(2) Welche Eigenschaften haben die Eigenzustände des Hamiltonoperators?
(3) Welche Eigenschaften besitzen die Matrixelemente Hmn = hm|H|ni des
Hamiltonoperators (in einer beliebigen Basis)? Aus welcher Eigenschaft
des Hamiltonoperators folgen sie?
(4) Welche Gleichung beschreibt die Zeitentwicklung eines quantenmechanischen Systems? Wie lautet sie?
(5) Wie sieht der Zeitentwicklungsoperator eines Systems aus, der die Entwicklung von einer Anfangszeit t0 zur Zeit t beschreibt? Was muss man
beachten, wenn der Hamiltonoperator des Systems explizit von der Zeit
abhängt?
6
1. Rückblick und Vorbereitung
(6) Wie sieht der Zeitentwicklungsoperator von der Zeit t0 zur Zeit t aus,
wenn im speziellen Fall der Hamiltonoperator nicht explizit von der Zeit
abhängt?
(7) Die Zeitentwicklungsgleichung lässt sich in dem Fall, dass der Hamiltonoperator nicht explizit von der Zeit abhängt, mittels eines Separationsansatzes lösen. Wie? Was ist die physikalische Bedeutung der dabei
auftretenden Separationskonstanten?
(8) Wie sieht die Zeitentwicklung eines Eigenzustands des Hamiltonoperators aus?
(9) Was ist ein stationärer Zustand? Wie drücken Sie einen solchen Zustand
durch Energieeigenzustände aus?
(10) Wie lautet der Hamiltonoperator des eindimensionalen harmonischen
Oszillators?
(11) Wie kann man diesen Hamiltonoperator durch die sogenannten Auf- und
Absteigeoperatoren â und ↠ausdrücken?
(12) Wie lauten die Vertauschungsrelationen dieser Operatoren?
(13) Können Sie eine explizite Repräsentation dieser Operatoren durch den
Ortsoperator x̂ und den Impulsooperator p̂ angeben?
(14) Wie lautet der Kommutator [x̂, p̂]?
(15) Zeigen Sie, dass Ihre Repräsentation der Operatoren â und ↠den Vertauschungsrelationen genügt!
(16) Wie wirken diese Auf- und Absteigeoperatoren auf den Grundzustand
des harmonischen Oszillators? Wie wirken sie auf andere Energieeigenzustände?
(17) Wie lauten die Wellenfunktionen der Energieeigenzustände des eindimensionalen harmonischen Oszillators?
(18) Geben Sie die Energieniveaus des eindimensionalen harmonischen Oszillators an!
(19) Wie sieht der Operator, der den Drehimpuls beschreibt, in Ortsdarstellung aus?
(20) Was ergibt sich für den Kommutator [r̂i , p̂j ] für i, j = 1, 2, 3? Wie berechnen Sie das?
(21) Welchen Vertauschungsrelationen genügen die Komponenten des Drehimpulsoperators?
(22) Mit welchem Operator vertauschen alle Komponenten des Drehimpulsoperators? Können Sie dies explizit durch sukzessive Anwendung der
Vertauschungsrelationen für die Komponenten zeigen?
Wiederholungsfragen
7
(23) Welcher Operator erscheint immer in der Schrödingergleichung für ein
System mit sphärischer Symmetrie?
(24) Wie werden die Eigenfunktionen des Drehimpulsoperators klassifiziert?
Zu welchen Operatoren sind sie Eigenfunktionen? Durch welche Quantenzahlen werden sie charakterisiert?
(25) Wie kann man mithilfe der Drehimpulseigenfunktionen die Lösung der
Schrödingergleichung eines Systems mit sphärischer Symmetrie erleichtern? Was ist die auftretende Konstante?
(26) Wie lautet die Orthogonalitätsrelation für die Kugelflächenfunktionen
Y`m (ϑ, ϕ)?
(27) Wie wirken die Operatoren L̂2 und L̂z auf die Kugelflächenfunktionen?
(28) Wie verhalten sich die Kugelflächenfunktionen unter der Paritätstransformation?
(29) Für ein Teilchen mit Spin s = 21 kann man eine Repräsentation des
Spinoperators mittels komplexer 2 × 2-Matrizen finden. Geben Sie diese
Matrizen in der Standarddarstellung an. Wie heissen diese Matrizen?
(30) Welchen Vertauschungsrelationen genügen diese Matrizen? Überprüfen
Sie das für Ihre Darstellung.
(31) Welchen Vertauschungrelationen genügen die Komponenten des Spinoperators Ŝ?
(32) Mit welchem Operator vertauschen diese Komponenten alle?
(33) Können Sie dies explizit mittels der Vertauschungsrelationen zeigen?
(34) Können Sie eine Basis für den Raum der Spinzustände zur obigen Repräsentation des Spinoperators angeben?
(35) Berechnen Sie in der Standarddarstellung Ŝ± = 21 Ŝx ± iŜy .
(36) Wie wirken die Operatoren Ŝ± auf die Basiszustände? Wie lauten die
Matrixelemente?
(37) Wie wirken Ŝ 2 und Ŝz auf die Basiszustände?
R
(38) Die Wellenfunktion ψ(r ) sei normiert mit d3 rψ ∗ (r )ψ(r ) = 1. Wie ist
die Größe |ψ(r )|2 zu interpretieren?
(39) Geben Sie den Ausdruck für die Wahrscheinlichkeitsstromdichte j(r, t)
an.
(40) Wie lautet die Kontinuitätsgleichung zwischen ρ(r, t) = |ψ(r, t)|2 und
j(r, t)?
(41) Beweisen Sie, dass die Lösungen der Schrödingergleichung die Kontinuitätsgleichung erfüllen.
(42) Durch welche Eigenschaft ist ein unitärer Operator definiert?
8
1. Rückblick und Vorbereitung
(43) Wie lautet die Wellenfunktion des Grundzustands des Wasserstoffatoms?
(44) Geben Sie die Energien der gebundenen Zustände des Wasserstoffatoms
an!
(45) Was gilt für die Erwartungswerte von kinetischer Energie hT i und potentieller Energie hV i in einem Coulombpotential ∼ 1r ? (Virialsatz!)
Kapitel 2
Zeitabhängige
Störungstheorie
2.1. Wechselwirkungsbild und Störungsentwicklung
Ausgangspunkt für die nachfolgenden Überlegungen ist ein Hamilton-Operator
der Form H = H0 + V (t) mit zeitunabhängigem H0 und einer explizit
zeitabhängigen Störung V (t). Es sollen folgende Voraussetzungen an V (t)
gestellt werden:
(1) V (t) “klein” im Vergleich zu H0
(2) V (t) = 0 für Zeiten t ≤ t0
Dann genügt die zeitliche Entwicklung des Systems für t ≤ t0 der ungestörten Schroedinger-Gleichung
∂ 0
|ψ (t)i = H0 |ψ 0 (t)i
∂t
und nach Einschalten der Störung der Gleichung
i~
∂
|ψ(t)i = [H0 + V (t)]|ψ(t)i
∂t
mit der Anfangsbedingung |ψ(t)i = |ψ 0 (t)i für t ≤ t0 .
i~
Wechselwirkungsbild. Ein diesem Problem angepasstes quantenmechanisches Bild ist das Wechselwirkungsbild.
Definition 2.1. Der Zustandsvektor
(2.1)
i
|ψ(t)iI = e ~ H0 t |ψ(t)i
heißt Zustandsvektor im Wechselwirkungsbild.
9
10
2. Zeitabhängige Störungstheorie
Satz 2.2. Die zeithabhängige Schrödinger-Gleichung
i~
∂|ψ(t)i
= [H0 + V (t)]|ψ(t)i
∂t
ist äquivalent zu
(2.2)
i~
∂
|ψ(t)iI = VI (t)|ψ(t)iI
∂t
i
i
mit VI (t) = e ~ H0 t V (t)e− ~ H0 t .
Beweis.
h
i
i
i
∂
∂ i
i~ |ψ(t)iI = i~ e ~ H0 t |ψ(t)i = −H0 e ~ H0 t + e ~ H0 t (H0 + V (t)) |ψ(t)i
∂t
∂t
i
i
i
= e ~ H0 t V (t)|ψ(t)i = e ~ H0 t V (t)e− ~ H0 t |ψ(t)iI
Gleichung 2.2 kann in die äquivalente Integralgleichung
Z
i t 0
dt VI (t0 )|ψ(t0 )iI
(2.3)
|ψ(t)iI = |ψ(t0 )iI −
~ t0
überführt werden. Diese wird iterativ gelöst durch die Reihenentwicklung
Satz 2.3 (von Neumann-Reihe).
Z
i t 0
|ψ(t)iI =|ψ(t0 )iI −
dt VI (t0 )|ψ(t0 )iI
~ t0
Z t0
Z t
1
(2.4)
dt0
dt00 VI (t0 )VI (t00 )|ψ(t0 )iI + . . .
− 2
~ t0
t0
2.2. Übergänge erster Ordnung in einem diskreten Spektrum
Untersucht werden nun Übergänge erster Ordnung in einem diskreten Spektrum unter der Wirkung der zeitabhängigen Störung V (t). Das System befinde sich zur Zeit 0 < t ≤ t0 in einem Eigenzustand |m(t)i von H0 .
(2.5)
i
i
|m(t)i = e− ~ H0 t |mi = e− ~ Em t |mi
mit |mi = |m(t = 0)i.
Zur Zeit t = t0 werde die Störung “eingeschaltet”. Gesucht ist die Wahrscheinlichkeit Wmn (t) für den Übergang vom Anfangszustand |mi in einen
Eigenzustand |n(t)i von H0 zu einer Zeit t nach Einschalten der Störung
V (t). Sie ist
(2.6) Wmn (t) = |hn(t)|ψ(t)i|2 ;
i
hn(t)|ψ(t)i = hn|e ~ H0 t |ψ(t)i = hn|ψ(t)iI
2.3. Beispiel: zeitlich konstante Störung, die bei t = t0 eingeschaltet wird11
Mit der Anfangsbedingung
i
i
i
|ψ(t0 )iI = |ψ 0 (t0 )iI = e ~ H0 t0 |m(t0 )i = e ~ H0 t0 e− ~ H0 t0 |mi = |mi
ergibt sich eingesetzt in die von Neumann-Reihe (1. Ordnung)
Z
i t 0
|ψ(t)iI = |mi −
dt VI (t0 )|mi
~ t0
und somit
hn(t)|ψ(t)i = hn|ψ(t)iI = hn|mi −
= δnm −
i
~
Z
t
dt0 e
i
~
Z
t
t0
dt0 hn|VI (t0 )|mi =
i
(En −Em )t0
~
t0
hn|V (t0 )|mi
Damit ist die Übergangswahrscheinlichkeit
Z
2
1 t 0 −iωmn t0
0
(2.7)
hn|V (t )|mi
Wmn (t) = 2 dt e
~
t0
mit ~ωmn = Em − En .
Für t0 → −∞ und t → ∞ ergibt sich:
(2.8)
Wmn
2
Z
1 ∞ 0 −iωmn t0
0
= lim Wmn (t) = 2 dt e
(t )|mi
- 9hn|V
t→∞
~
−∞
t0 →−∞
2.3 Beispiel
2.3. Beispiel: zeitlich konstante Störung, die bei t = t0
eingeschaltetZeitlich
wird konstante Störung, die bei t = t0 eingeschaltet wird.
V0
V̂(t) = V̂0 θ(t − t0 )
t
t0
Es ist
Setze t0 = 0 . Mit ωmn = (Em − En )/h̄ gilt:
Z
!! iω t/h̄
!!22
!" 2
!2 2
2 e−iωmn t −
mn t
mn
! 1 |!n|V̂0|m"|22 !! e−iω
1 t 0 −iωmn t0 1 ! t ! i(E
|hn|V
|mi|
!
−−11!!!!
0
i(E
−E
)t/h̄
−E
)t
/h̄
n
m
n
!
! 0 |midt e= m
!
!
Wmn (t) = 2 W
dtmn
e (t) = hn|V
!n|
V̂0ω|m"
!!
!!
! =
~
~2
ωωmn
mn
0
h̄2 ! 0
h̄22
mn
!2
t
|hn|V0 |mi|2 2
|hn|V0 |mi|2 sin ωmn
2
=
(1
−
cos
ω
t)
=
mn
ωmn
2
~2
ωmn
~2
!
2
t "2
2
|!n|V̂0 |m"|2 sin ωmn
|!n|V̂0 |m"| 2
2
(1 − cos ωmn t) =
=
Dies liefert
ωmn t
2
ωmn
h̄2
h̄2
2
2 ωmn t
π sin 2
2
(2.9)
Wmn (t) = 2 t
|hn|V
|mi|
0
~ π ωmn2 2ωtmn t
=
2
π sin
2
2
! ω t "2 |!n|V̂0 |m"|
2t
mn
h̄ π
t
2
12
2. Zeitabhängige Störungstheorie
- 10 -
sin2 ωt
nun die Funktionenfolge δt (ω) =
πω 2 t
nschaften:
. ω=0
und δt (ω) <
δt (ω)
1
... ω != 0
πω 2 t
t die Delta-Distribution
! +∞
= δ(ω) mit
dω δ(ω)F (ω) = F (0)
ω
π/t
−π/t
−∞
e Übergangswahrscheinlichkeit im Grenzfall “langer” Beobachtungszeit t :
Abbildung 2.1. δ (ω)
(t) =
t→∞
!
!2 2π t
!
!2 t
π
!
!
!
!
2 t δ(ωmn /2) !!n|V̂0 |m"! = h̄ δ(Em − En ) !!n|V̂0 |m"!
h̄
Untersuche die Funktionenfolge
e verwendet:
!
Em − En
δ(ωmn /2) = δ(2.10)
2h̄
"
2
= 2h̄ δ(Em − En ) δ) (ω) = sin ωt
t
2
πω t
Man
sieht δt (ω) =
gangswahrscheinlichkeit pro
Zeit:
t
π
bei ω = 0 und δt (ω) <
1
πω 2 t
für ω 6= 0.
Diese Funktionenfolge konvergiert im Limes großer t gegen die DeltaDistribution:
(2.11)
lim δt (ω) = δ(ω)
t→∞
R∞
mit −∞ dωF (ω)δ(ω) = F (0).
Im Grenzfall langer Beobachtungszeit t → ∞ geht dann die Übergangsmerke:
wahrscheinlichkeit
Bei zeitlich konstanter Störung und t → ∞über
: in
ω 2π
t→∞ π Energie
mn möglich.
Übergang nur zwischen Zuständen
gleicher
Wmn (t)
−→
tδ
|hn|V0 |mi|2 =
tδ(Em − En )|hn|V0 |mi|2
~2
2
~
Die Übergangswahrscheinlichkeit pro Zeit ist dann gegeben durch
(2.12)
Wmn
2π
=
δ(Em − En )|hn|V0 |mi|2
t→∞
t
~
Γmn = lim
2.4. Zeitlich periodische Störungen, Fermis Goldene Regel
Gegeben sei nun eine Störung der Form
(2.13)
V (t) = V0 e−iωt Θ(t)
Mit 2.3 erhält man dann die Übergangswahrscheinlichkeit
Z
2
1 t 0 i (En −Em −~ω)t0
~
hn|V0 |mi
Wmn (t) = 2 dt e
~
0
dische Störungen; Fermi’s Goldene Regel
eriodische Störung V̂(t) , die zur Zeit t = 0 eingeschaltet wird:
V̂(t) = V̂0 e−iωt
θ(t)
2.4. Zeitlich periodische Störungen, Fermis Goldene Regel
13
ationen aus 2.2, jedoch mit
und im Grenzfall t → ∞:
!" t
!2
!
!
!
1
Wmn ! 2π
/h̄
2
dt! ei(En −Em −h̄ω)t
V̂
|m"
= 2 !!
Γm→n !n|
= lim
=
0 t ! ~ δ(En − Em − ~ω) |hn|V0 |mi|
t→∞
h̄
0
Übergänge im kontinuierlichen
Spektrum.
man die Übergangswahrscheinlichkeit
pro Zeiteinheit
n
Definition! 2.4 (Zustandsdichte).
Die Zahl der Zustände dN (E) mit Ener!2
2π
!
!
im Energieintervall [E, E + dE] definiert die Zustandsdichte
δ(En − Emgie−Eh̄ω)
=
!"n|V̂0 |m#!
h̄
dN (E)
(2.14)
ρ(E) =
(stationäre) Zustand |m! geht durch AbsorptiondE
eines
in den (ebenfalls stationären) Zustand |n! über.
nuierlichen Spektrum:
ρ(E)
hl der Endzustände dN(E)
ergieintervall [E, E+dE]):
)=
dN (E)
dE
E
diskretes Spektrum
kontinuierliches Spektrum
Abbildung 2.2. Zustandsdichte
Die Übergangswahrscheinlichkeit pro Zeit summiert über alle möglichen
Endzustände |ni geht dabei über in das Integral
Z
Z
dN (En ) Γmn = dEn ρ(En )Γmn
Z
2π
=
dEn ρ(En )δ(En − Em − ~ω)|hn|V0 |mi|2
~
Damit erhält man “Fermis Goldene Regel”
(2.15)
mit Ef = Em + ~ω.
Γ=
2π
ρ(Ef ) |hf |V (t = 0)|mi|2
~
14
2. Zeitabhängige Störungstheorie
2.5. Elektromagnetische Übergänge
Gegeben Sei eine elektromagnetische Stromdichte j(x). Die Wechselwirkung
zwischen dem Strom und einem äußeren elektromagnetischen Feld ist in der
Coulomb-Eichung (transversale Eichung)
div A = 0,
durch den Ausdruck
1
V (t) =
c
(2.16)
Z
Φ=0
j(x) · A(x, t) d3 x
gegeben. Dabei ist Vektorpotential A(x) Lösung der (homogenen) Wellengleichung
1 ∂2
2
− ∇ Ai (x, t) = 0
c2 ∂t2
und von der Form
~∗ −ik·x+iωt )
A(x, t) = N (~ε| eik·x−iωt
{z } + ε| e {z
}
(2.17)
Absorption
Emission
mit dem Polarisationsvektor ~ε. Es gilt ω = c|k|.
Die elektrischen und magnetischen Felder sind in dieser Eichung mit dem
Vektorpotential verknüpft über
1∂
A(x, t), B(x, t) = rot A(x, t) = ∇ × A(x, t)
c ∂t
Mit der Energie des Strahlungsfeldes
Z
1
Eγ =
|E|2 + |B|2 d3 x = ~ω
8π V
E(x, t) = −
erhält man eingesetzt
1
Eγ =
8π
Z V
1
|Ȧ|2 + |k × A|2
c2
d3 x
und damit die Normierungskonstante in 2.17
r
2π~c
N =
, k = |k|
kV
Betrachtet werde nun ein Übergang von einem Energieeigenniveau |ai
in ein Energieeigenniveau |bi. Nach 2.15 ist die Übergangswahrscheinlichkeit
pro Zeit
Γa→b =
2π
ρ(Eb = Ea + ~ω)|hb|V (t = 0)|ai|2
~
15
2.6. Elektrische Dipolübergänge
mit
V (0) =
r
2π~
ωV
Z
j(x) · ~ε eik·x d3 x
j(x) ist die stationäre Stromdichte des absorbierenden Systems
e
ĵ(x) = en(x) v̂ = n(x)
p̂
|{z}
| {z }
m
Impulsop.
Ladungsdichte
e2
1
(wobei hier das cgs-System mit ~c = 137.03...
verwendet wird, ~c = 1.973 ×
3
10 eVÅ) Für ein punktförmiges Teilchen mit Masse m und Ladung e ist
n(x) = δ 3 (x − r) und somit
(2.18)
Γa→b =
4π 2 e2
p
ρ(Eb = Ea + ~ω)|hb|eik·r ~ε · |ai|2
ωV
m
2.6. Elektrische Dipolübergänge
Seien |ai und |bi diskrete Zustände in einem Atom mit
H0 |ai = Ea |ai,
H0 |bi = Eb |bi
In der Atomphysik ist k · r ≈ kR 1 (R Atomradius), was hervorgeht aus
der Abschätzung
~ω
10 eV Å
ω
R=
R≈
≈ 10−2
c
~c
2 × 103 eV Å
Dies rechtfertig die Dipol-Näherung
kR =
(2.19)
eik·r = 1 + ik · r + · · · ≈ 1
Nimmt man an, dass die Polarisation des Lichts linear ist ~ε = ez =
(0, 0, 1), so erhält man als Übergansmatrixelement
pz
hb| |ai = hb|ż|ai
m
welches man mit der Bewegungsgleichung des Ortsoperators im Wechselwirkungsbild
i
ṙ = [H0 , r]
~
schreiben kann als
pz
i
i
hb| |ai = hb|H0 z − zH0 |ai = (Eb − Ea )hb|z|ai
m
~
~
Die Wahrscheinlichkeit pro Zeit für einen elektrischen Dipolübergang ist
damit nach 2.18
4π 2 e2
Dipol
(2.20)
Γel.
=
ωρ(Eb = Ea + ~ω)|hb|z|ai|2
a→b
V
R
Das Matrixelement hb|z|ai berechnet man in Ortsdarstellung über ψb∗ (r)zψa (r) d3 r.
16
2. Zeitabhängige Störungstheorie
2.7. Ergänzung zur Wechselwirkung geladener Teilchen mit
dem elektromagnetischen Strahlungsfeld
Zur Erinnerung: der Hamilton-Operator eines geladenen Teilchens (z.B.
Elektron) im elektromagnetischen Feld ist
i2
1 h
e
(2.21)
H=
p − A(x, t) + eΦ(x, t) = H0 + V (t)
2m
c
mit einem Wechselwirkungsoperator
(2.22)
V (t) = −
e
e2
{p, A(x, t)}+ +
A2 (x, t) + eΦ(x, t)
2mc
2mc2
Dabei wurde der Antikommutator {p, A}+ = p·A+A·p = −i~(∇·A+A·∇)
verwendet.
Für ein System von N punktförmigen, geladenen Teilchen ist
V (t) =
N X
i=1
e2
e
{pi , A(xi , t)}+ +
A2 (xi , t) + eΦ(xi , t)
−
2mc
2mc2
Mit der Teilchendichte
n(x) =
N
X
i=1
δ 3 (x − xi )
und der Stromdichte
N
e X
{pi , δ 3 (x − xi )}+
j(x) =
2m
i=1
kann man das Wechselwirkungspotential auch allgemeiner schreiben als
(2.23)
Z 1
e2
2
j(x) · A(x, t) +
n(x) · A (x, t) + en(x)Φ(x, t) d3 x
V (t) =
c
2mc2
Quantisierung des Strahlungsfeldes. Der Vakuumzustand (keine Photonen) werde durch den Zustand |0i beschrieben, der Zustand eines Photons
mit Wellenvektor k und Polarisationszustand λ durch |k, λi. Außerdem werde ein Erzeugungsoperator definiert durch
(2.24)
|k, λi = a†k,λ |0i
und ein Vernichtungsoperator
(2.25)
ak,λ |k, λi = |0i,
ak,λ |0i = 0
17
2.7. Wechselwirkung mit dem e.m. Strahlungsfeld
Das Vektorpotential kann damit dargestellt werden als Fourier-Integral
bzw. Fourier-Summe
r
i
X 2π~c h
∗
(2.26) A(x, t) =
ak,λ ~εk,λ eik·x−iωk t + a†k,λ ~εk,λ
e−ik·x+iωk t
kV
k,λ
mit |{z}
~ω = ~|k| c.
|{z}
Energie
- 13 -
Impuls
Die Normierung wurde so gewählt, dass
Z
X
2
3
1
1
†
2
|E| + |B| d x =
~ωk ak,λ ak,λ +
(2.27)
HPhoton =
8π
2
2.5 Beispiel: Elektromagnetische Übergänge
k,λ
gilt die Vertauschungsrelation
|a! und |b!
Betrachte zwei Es
Zustände
und angeregter Zustand eines Atoms,
i
h (z.B.: Grundzustand
†
ak,λ
eines Moleküls (2.28)
oder eines Atomkerns ...
) , ak0 ,λ0 = δkk0 δλλ0
(Bosonen-Kommutator).
Übergang durch Absorption oder Emission eines Photons (Lichtquants) mit der Energie h̄ω
|b!
|b!
|a!
|a!
h̄ω
h̄ω
1
c
!
Abbildung 2.3. Graphische Darstellung eines strahlungsinduzierten Übergangs
Wechselwirkungsoperator:
V̂ (t) =
! x) · A(!
! x, t)
d3 x J(!
Stromdichte
Vektorpotential:
! · A(!
! x, t) = 0
mit ∇
Φ = 0 in der Coulomb-
"
!
i!
k·!
x−iωt
∗ −i!
k·!
x+iωt
!
A(!x, t) = N !ε e
+ !ε e
Absorption
Emission
Elektrische und magnetische Felder:
!
! = − 1 ∂A
E
c ∂t
Vektorpotential des
elektromagn. Feldes
! =∇
! ×A
!
B
(transversalen) Eichung
ω = c |"k|
18
2. Zeitabhängige Störungstheorie
Übungsaufgaben zu
Kapitel 2
Aufgabe 1
Ein Teilchen mit Spin 1/2 und dem magnetischen Moment µ
~ = µ0 ~σ sei
in einer “Fallelokalisiert, die sich in einem homogenen, zeitlich konstanten
Magnetfeld B0 befindet. Die Richtung von B0 definiere die z-Achse eines
Koordinatensystems. Im Grundzustand |−i = |ms = −1/2i sei der Spin in
negativer z-Richtung polarisiert. Die Energie dieses Zustandes sei E− . Der
angeregte Zustand |+i = |ms = +1/2i besitze die Energie E+ .
a) Drücken Sie die Energiedifferenz E+ − E− = ~ω durch µ0 und |B0 | aus.
b) Wie lautet die Zeitabhängigkeit der Zustände |ψ± (t)i, wenn diese zur
Zeit t = 0 mit |ψ+ (t = 0)i = |+i bzw. mit |ψ− (t = 0)i = |−i identifiziert
werden?
Nun wirke zusätzlich eine zeitabhängige Störung V̂ (t) = −~
µ · ∆B(t) mit
∆B(t) = (∆Bx , 0, 0)T und
∆Bx (t) =
b0
0
0 ≤ t ≤ ∆t
sonst.
c) Berechnen Sie die Matrixelemente hj|V̂ (t)|ii mit i, j ∈ {+, −}.
d) Man formuliere die Wahrscheinlichkeit W+− für den Übergang |−i →
|+i unter dem Einfluß der Störung V̂ (t). Diskutieren Sie den Verlauf
von W+− (∆t) als Funktion des Zeitintervalls ∆t.
e) Untersuchen Sie das Verhalten der Übergangswahrscheinlichkeit pro Zeit,
Γ+− = W+− /(∆t), im Grenzfall ∆t → ∞.
Aufgabe 2
Ein Wasserstoffatom gehe durch die Emission eines Lichtquants der
Energie ~ω von einem diskreten, angeregten Zustand |bi in den Grundzustand |ai über. Die Übergangswahrscheinlichkeit pro Zeit lautet nach Fermis
Goldener Regel
Γb→a
−ik·r ~ε · p̂ 2
4π 2 e2
b .
δ(Eb − Ea − ~ω) a e
=
ωV
m 19
Übungsaufgaben zu Kapitel 2
(Hier ist e2 /(~c) ' 1/137). Dabei ist V das Normierungsvolumen für das
elektromagnetische Feld, p̂ = −i~∇ ist der Impulsoperator, ~ε ist der Polarisationsvektor und k ist der Wellenvektor des emittierten Photons.
a) Wiederholen Sie die Schritte zur Herleitung von Γb→a .
b) Schätzen Sie ab, dass für elektromagnetische Übergänge im diskreten
Spektrum von Atomen die Dipolnäherung e−ik·r ' 1 gilt. Zeigen Sie
damit
4π 2 e2
ΓDipol
=
ωδ(Eb − Ea − ~ω) |dab · ~ε |2 ,
b→a
V
wobei dab = ha|r|bi.
c) Für die in das Raumwinkelelement dΩ im k-Raum emittierte Strahlungsleistung gilt
Z
dkk 2
~ω Γb→a .
dP = V dΩ
(2π)3
Man zeige, dass dann in der Dipolnäherung mit ω = (Eb − Ea )/~ gilt
dP
e2 4
=
ω |dab · ~ε |2 .
dΩ
2πc3
d) Angenommen, das Wasserstoffatom emittiere linear polarisiertes Licht
mit ~ε = ez = (0, 0, 1)T . Der angeregte Zustand |bi sei charakterisiert
durch den Bahndrehimpuls lb und die magnetische Quantenzahl mb (der
Spin werde vernachlässigt). Welche Werte (lb , mb ) werden beim Übergang in den Grundzustand |ai selektiert?
Aufgabe 3
Ein linearer harmonischer Oszillator mit Masse m und Ladung q befinde sich
zur Zeit t → −∞ in seinem Grundzustand. Zur gleichen Zeit wird ein ho2
mogenes, zeitabhängiges elektrisches Feld E(t) = E0 ez e−βt eingeschaltet
(ez ist der Einheitsvektor in z-Richtung).
(1) Man berechne die Wahrscheinlichkeit, mit welcher der Oszillator für
t → ∞ im Grundzustand verbleibt.
(2) Unter welchen Bedingungen ist Störungstheorie 1. Ordnung anwendbar?
Aufgabe 4
In einem System aus Wasserstoffatomen befinden sich N0 Atome zur Zeit
t = 0 im angeregten 2p-Zustand. Durch Photonenemission gehen sie in den
Grundzustand über. Die Strahlungsleistung pro Atom ist gemäß Aufgabe 2
gegeben durch
dP
dΩ
=
e2 4
ω |d21 · ~ε ∗ |2 .
2πc3
20
2. Zeitabhängige Störungstheorie
Ein Analysator misst linear polarisiertes Licht mit ~ε ∗ = ez (der Polarisationsvektor ist der Einheitsvektor in z-Richtung).
(1) Man berechne das Dipol-Matrixelement
d21 · ~ε ∗ = h1s |z| 2pi
und bestimme
dP
dΩ .
Hinweise: Die Wellenfunktionen des Wasserstoffatoms für 1s- und 2pZustände lauten (mit a = ~2 /(me2 ) = 0.53 · 10−8 cm, r̂ Einheitsvektor
in Richtung von r):
Ψnlml (r) = Rnl (r)Ylml (r̂)
R10 (r) =
Y00 (θ, ϕ) =
√1 ,
4π
2
e−r/a ,
a3/2
Y10 (θ, ϕ) =
q
R21 =
3
4π
√
1
r −r/(2a)
e
3(2a)3/2 a
q
3
cos θ, Y11 (θ, ϕ) = − 8π
sin θ eiϕ .
(2) Schätzen Sie aus der abgestrahlten Leistung P ' ~ω
τ die charakteristische Lebensdauer τ im angeregten Zustand (bzw. die Dauer des optischen Übergangs) ab. Was finden Sie beim Vergleich mit dem Literaturwert? Was könnte die Ursache sein?
(3) (Zusatzaufgabe) Wie ändert sich das berechnete Ergebnis für die Lebensdauer, wenn man nicht nur linear polarisiertes Licht betrachtet, sondern
alle möglichen Polarisationszustände berücksichtigt? Welche Übergänge
sind möglich? Begründen Sie, dass dann die abgestrahlte Leistung eines
Atoms in einem unpolarisierten Ensemble gegeben ist durch
dP
dΩ
=
e2 4 X
ω
2πc3
X
λ=1,2 m=0,±1
pm |h21m|x · ~ελ∗ |1si|2 ,
wobei über die jeweils zwei möglichen Polarisationszustände ~ελ∗ des auslaufenden Photons summiert wird. Betrachten Sie insbesondere rechtsund linkszirkulare Polarisationszustände mit ~ε1,2 = √12 (ex ± iey ). Was
ist in einem solchen Ensemble von Atomen für die Wahrscheinlichkeit pm
anzusetzen, ein Atom im Zustand |21mi mit Quantenzahl m zu finden?
Was ergibt sich damit als Ergebnis für die Lebensdauer?
(4) Zu einer Zeit t > 0 befinden sich noch N (t) Atome im angeregten Zustand. Das Zerfallsgesetz lautet dN = −τ −1 N (t) dt. Bestimmen Sie N (t)
und die Wahrscheinlichkeit W (t) für das Verbleiben im angeregten Zustand zur Zeit t.
(5) Für die Wellenfunktion des zerfallenden Zustandes gilt mit ψ2p (r, t =
0) = u(r)
p
ψ2p (r, t) = u(r ) c(t) e−iE2p t/~ , c(t) = W (t).
21
Übungsaufgaben zu Kapitel 2
Man zeige:
t
,
ψ2p (r, t) = u(r)f (t) mit f (t) = exp −iω2p t −
2τ
wobei ω2p = E2p /~ und f (t) = 0 für t ≤ 0.
(6) Durch Fouriertransformation,
Z ∞
g(ω) =
dt eiωt f (t),
−∞
zeige man, dass die Spektrallinie des angeregten 2p-Zustandes die Form
einer Lorentz-Kurve annimmt:
1
|g(ω)|2 ∝
,
(ω − ω2p )2 + Γ2 /4
mit Γ = τ1 . Diskutieren Sie dieses Ergebnis.
Teil 2
Elemente der
quantenmechanischen
Streutheorie
Kapitel 3
Streuung
I
+
h
L,I
I
3-1
h
+R
il
kR
ils
sN
I,{
h tr,
t
s
m
\
L,I
3.1. Streuprozess und Wirkungsquerschnitt
d
fr.
X
t
X
o
I
o
$/tu
o
qo
h
i-
tl
'lN
)r
p
tl
'lN
,-N
)r
p
J
\
s
qo
h
i-
\
J
s
,-N
. a - - . - \
r
N
a
s
(\
= r2 dθ sin θ dϕ
r
a
s
2
(\
o
$
s-
illl
x=
cosdΩ
ϕ
Flächenelement auf Kugel mit Radius
r: r sin θ r
N
e\S
Sl
l+
e\S
s-
't
sg
o
s
Ers S
]R
+ fl ?,0
pr
illl
9I
]R
?,0
sg
ll
!eθ = cos
cosBeschreibung
ϕ !ex + cos θam
sinbesten
ϕ !ey −
sin θ !ez Koordinatensystem sind die
Dasθder
angepasste
in 3ϕDimensionen:
!eϕ Polarkoordinaten
= − sin ϕ !ex + cos
!ey
y = r sin θ sin ϕ
z = r cos θ
mit einem Satz von Einheitsvektoren
25
$/tu
,vo$oh,pJl +
. a - - . - \
h,pJ
g,E
sl
oo
s ,vo$
\ruI
g,E-Ss
sl
s oo
P. p'
o
t
vI
s th.
-Ss
\oJ
Sl \ruIss
o
s
s th.Ersfl S
pr
\oJ ss+
't
P.$p'
:
ll
(vso0
n{s'S'
?{JJe G/
9I\q bh .t
xN
N
o
bh
(vso0
n{s'S'
Jbr
r9t
9.1,N\
h
f)
{JJ
x
behandelt werden.
N
N
NO
!\
!r
ss\6
dl' 1
V,FJ
(.,-\
ss\6
NO
!\
1
dl' 1
V,FJ
1
t
tv
il
:
tr,l ?
N
h
f)
il No
? G/
?e
\q+' .t
N]
x Zunächst
= r sin θsoll
cos
ϕ
!
die elastische Streuung
y = r sin θ sin ϕ
r = x2 + y 2 + z 2
z = r cos θ
A + B −→ A + B
!er = sin θ cos ϕ !ex + sin θ sin ϕ !ey + cos θ !ez
r9t Jbr 9.1,N\
o
o
Polarkoordinaten in 3 Dimensionen
tr,l
+'
N]
(.,-\
(^
(^
N
N a
fr.
I
!r aI d
l
J b0
l a
J
\
0 n,
h
ah
n,h
hE
R
h
\
Skizze: Elastische Streuung eines Strahls von
Teilchen A an einem Target (Teilchen B)
\
\
\
h
E
R q;?
h
I
? $
q;
h
A
I Am
$s
h
F\
tr,
s
F\
t\
3.1 Streuprozess und Wirkungsquerschnitt
b
t
kt\ I,{
Ns
Betrachtet werden der
im Folgenden
quantenmechanische Streuprozesse.
3. Grundbegriffe
quantenmechanischen
Streutheorie
J
d
ss\6
!r
fr.
N
N
X
o
qo
h
i-
tl
'lN
,-N
)r
p
J
s
\
r
N
a
s
(\
$/tu
o
qo
h
i-
tl
'lN
)r
p
\
J
s
,-N
. a - - . - \
r
N
(\
s
a
h,pJ
r2 dΩ = r2 dθ sin θ dϕ
$/tu
. a - - . - \
h,pJ
g,E
sl
oo
s ,vo$
\ruI
l+
e\S
g,ESl
sl
ooo
s ,vo$
s-
o
e\S
$
s-
't
sg
s
Ers S
]R
+ fl ?,0
pr
illl
o
9I
cos θ cos ϕ !ex + cos θ sin ϕ !ey − sin θ !ez
− sin ϕ !ex + cos ϕ !ey
]R
?,0
sg
X
ss\6
t
o
I
l+
s th.
-Ss
\oJ
Sl \ruIss
P. p'
-Ss
o
t
vI
s
s th.Ersfl S
pr
\oJ ss+
't
P.$p'
?
o
(vso0
n{s'S'
:
?e
9I\q bh .t
{JJ
ll
x
N
G/
bh
(vso0
n{s'S'
r9t Jbr 9.1,N\
h
N
o
x = r sin θ cos ϕ
!
y = r sin θ sin ϕ
r = x2 + y 2 + z 2
z = r cos θ
sin θ cos ϕ !ex + sin θ sin ϕ !ey + cos θ !ez
henelement auf Kugel mit Radius r:
3. Streuung
NO
!\
1
NO
!\
V,FJ
(.,-\
dl' 1
dl' 1
1
t
tv
tr,l ?
il
:
il N
? e G/
\q+' .t
N
o
h
f)
o
arkoordinaten in 3 Dimensionen
tr,l
+'
N]
26
V,FJ
(.,-\
(^
(^
N
N a
fr.
I
!r aI d
l
J
l
b
h
0
b
h
ah
n,h
h
\
\
E
R q?
h
\
\
\
h
\
?
q;
h
s
h
A
I
$
h
mts
t
tr,
s
kizze: Elastische Streuung eines Strahls von
Teilchen A an einem Target (Teilchen B)
er = sin θ cos ϕ ex + sin θ sin ϕ ey + cos θ ez
eθ = cos θ cos ϕ ex + cos θ sin ϕ ey − sin θ ez
eϕ = − sin ϕ ex + cos ϕ ey
Das infinitesimale Flächenelement
df = r2 dΩ = r2 dθ sin θdϕ
bestimmt das Integrationsmaß.
Zentral für die weitere Behandlung ist
Definition 3.1 (Differenzieller Wirkungsquerschnitt). Man nennt die differentielle Größe
(3.1)
dσ =
Strom der in Richtung (θ, ϕ) gestreuten Teilchen 2
r dΩ
Strom der in z − Richtung einfallenden Teilchen
den differentiellen Wirkungsquerschnitt, den man auch in Form eines
Differentialquotienten schreiben kann
jgestreut (θ, ϕ) 2
dσ
=
r
dΩ
jeinfallend
(3.2)
und welcher die Dimension einer Fläche [L2 ] hat.
3.2. Nichtrelativistische Potentialstreuung
Behandelt werden soll nun ein Spezialfall der elastischen Streuung, nämlich
der eines nichtrelativistischen Streuvorgangs, der durch ein reelles, zeitunabhängiges und nicht geschwindigkeitsabhängiges Potential V = V (rA −rB )
dargestellt werden kann. Die Kinematik wird dabei durch den HamiltonOperator
(3.3)
H=−
~2
~2
∆r A −
∆r + V (rA − rB )
2mA
2mB B
27
3.3. Stationäre Streuwellenfunktion
beschrieben. Die Schrödinger-Gleichung für die Ortswellenfunktion lautet
dann
∂
(3.4)
HΨ(rA , rB ; t) = i~ Ψ(rA , rB ; t)
∂t
Nach Übergang in Schwerpunkts- und Relativkoordinaten
mA ra + mB rB
R=
Gesamtmasse M = mA + mB
M
r = rA − rB , v = vA − vB
und Einführen des Gesamtimpulses
P = pA + pB
sowie des Relativimpulses
mA mB
mB pA − mA pB
= mv mit der reduzierten Masse m =
p=
M
M
nimmt der Hamilton-Operator die Gestalt
P2
p2
+
+ V (r)
2M
2m
an. Somit separieren die Schwerpunkts- und Relativbewegung
(3.5)
(3.6)
H=
i
i
Ψ(rA , rB ; t) = Φ(R, r)e− ~ Et = ϕ(R)ψ(r)e− ~ Et
Die Schrödinger-Gleichung 3.4 ist dann äquivalent zu den beiden Gleichungen
~2
P2
−
∆R ϕ(R) = ECM ϕ(R) mit ECM =
2M
2M
2
~
∆r + V (r) ψ(r) = Er ψ(r) mit E = ECM + Er
−
2m
Oft ist es praktisch, das Schwerpunktsystem zu wählen mit P = 0. Hier gilt
E = Er .
3.3. Stationäre Streuwellenfunktion
Definition 3.2 (Reduziertes Potential). Man nennt
(3.7)
U (r) =
2m
V (r)
~2
reduziertes Potential.
Damit nimmt die Schrödinger-Gleichung mit “scharfer” Energie
E=
~2 k 2
2m
28
3. Streuung
und Impuls p = ~k, k = |k|ez die Form einer Wellengleichung
(3.8)
∆ + k 2 − U (r) ψ(r) = 0
an.
Im Folgenden nimmt man an, dass das Potential asymptotisch abfällt
(V (r) → 0 für r → ∞) schneller als 1r . Diese Annahme ist in den meisten
Fällen erfüllt, zum Beispiel auch für das abgeschirmte Coulomb-Potential
−µr
(Yukawa-Potential) V (r) ∝ e r . Die Behandlung des reinen CoulombPotentials erfordert neue Methoden, die Kapitel 3.9 behandelt werden.
5
Gesucht wird nun eine stationäre3 -Lösung
der Schrödinger-Gleichung
ψk (r) = ψ(k, r) mit folgenden Randbedingungen
• einfallende Welle in positiver z-Richtung
• vom Streuzentrum auslaufende Welle
Asymptotische Form der vollen Lösung für r → ∞ :
für
elastische
Streuung:
|!k ! | = |!k|
!k ! = k !er = k !r
r
!
"
Dazu wird zunächst die freie Lösung der homogenen Wellengleichung
eikr
(+) "
i!
k·!
r
(für U = 0) ψ
betrachtet
(k, "r ) −→ A e
+ f (θ, ϕ)
(3.9)
(+)
ψ0 (k, r) = Aeik·r = Aeikz
!
k
r
Die asymptotische Form der vollen Lösung (für r → ∞) ist dann


(3.10)
einlaufende

ebene Welle
 ik·r
r→∞
ψ (+) (k, r) −→ A 
 e|{z} +
einlaufende
fk (θ, ϕ)
| {z }
eikr
r
|{z}
auslaufende


Kugelwelle



Streuamplitude
WelleStreuamplitude
auslaufende
Kugelwelle
3.4. Streuung von Wellenpaketen
Bei der vorherigen Diskussion stößt man auf das Problem, dass die stationäre Wellenfunktion ψ (+) (k, r) nicht normierbar ist. Daher wählt man als
Ausgangspunkt einer exakteren Behandlung die Streuung eines Wellenpakets.
3.4 Streuung von Wellenpaketen
Stationäre Lösung ψ (+) ("k, "
r ) mit “scharfer” Energie ist nicht normierbar !
3.5. Differentieller Wirkungsquerschnitt dσ/dΩ
29
Betrachte die Streuung eines lokalisierten (normierbaren) Wellenpakets:
ist allgemein von der Form
und hierzu dieDieses
Lösung
der zeitabhängigen
Schrödingergleichung
Z
3
i
d k
(+)
A(k)ψ
(k, r)e− ~ Ek (t−t0 )
ψ(r, t) =
"
3
h̄2 ! 2 (2π)
∂
2
2
∇
+
V
(!
r
)
ψ(!
r
,
t)
=
ih̄
ψ(!r, t)
~−
k
wobei Ek = 2m und muss der zeitabhängigen Schrödinger-Gleichung
2m
∂t
~2
∂
(3.12)
−
∆ + V (r) ψ(r, t) = i~ ψ(r, t)
geeigneten asymptotischen2mRandbedingungen
und
Anfangsbedingung bei
∂t
3 - 6a
mit geeigneten asymptotischen Randbedingungen und Anfangsbedingung
h̄2 k 2
beiWellenpaket:
t = t0 gehorchen.
Superposition von stationären Wellenfunktionen mit Ek =
(3.11)
mit
!
2m
Das Wellenpaket ist !also 3die Superposition von stationären Wellenfunkd k
(+) "
)/h̄
"k) ψImpulsverteilung
A(
(k, "r ) e−iEk (t−t0(Distribution
r, t) = Ek und
tionen mit der ψ("
Energie
der
im k(2π)3
Raum) A(k). Die asymptotische Lösung für t → ∞ (d.h. r → ∞) ist
und einer Impulsverteilung / Distribution im k-Raum A(k)
Asymptotische Lösung für t → ∞ : (d.h. r → ∞)
3
" ik·r
#
eikr
3d k
ikr
k (t−t0 )
d
k
e
(3.13)
A(k) i!k·!
e
+ fk (θ, ϕ)
e−iE(t−t
−iE
0)
3 "
A(
k) e r + f!k (θ,
ϕ)
(2π)
r e k
3
(2π)
r
Für eine Distribution A(k) mit geringer Breite um k0 wird der StreuprozessFür
durch
eine stationäre
Lösung
mit
“scharfem”
Impuls
~k0 beschrieben.
geringer
Breite
um k0 wird
der Streuprozess
A(k) mit
eine Distribution
!
ψ(r, t) →
ψ("r, t) −→
Z
durch ein stationäre Wellenfunktion mit “scharfem” Impuls h̄k0 beschrieben.
3.5. Differentieller Wirkungsquerschnitt dσ/dΩ
Die quantenmechanische Stromdichte ist
~ ∗
~
∗
∗
[ψ (r)∇ψ(r) − ψ(r)∇ψ (r)] = Re
ψ (r)∇ψ(r)
(3.14) j(r) =
2mi
mi
t = t0 .
30
3. Streuung
Diese erfüllt mit der Wahrscheinlichkeitsdichte
(3.15)
n(r) = |ψ(r)|2 = ψ ∗ (r)ψ(r)
die Kontinuitätsgleichung
∂n(r, t)
=0
∂t
Für stationäre Wellen (n(r) unabhängig von t) gilt dann
(3.16)
(3.17)
∇ · j(r, t) +
∇ · j(r) = 0
Die radiale Komponente des Stroms für r → ∞ ist
e−ikr ∂
~
eikr
j·er = |A|2 Re
e−ikr cos θ + fk∗ (θ, ϕ)
eikr cos θ + fk (θ, ϕ)
mi
r
∂r
r
Die einlaufende Stromdichte ergibt sich aus ψein (r) = Aeik·r = Aeikz zu
~k
|jein | = |A|2
= |A|2 v
m
mit der Geschwindigkeit v = ~k
m . Für die radial auslaufende Welle ist die
Stromdichte (r → ∞)
~ ∗
e−ikr ∂
eikr
2
jaus (r) · er = |A| Re
f (θ, ϕ)
fk (θ, ϕ)
mi k
r ∂r
r
v
1
= |A|2 2 |fk (θ, ϕ)|2 + O( 3 )
r
r
Der durch das Flächenelement r2 dΩ auslaufende Fluss ist damit
|A|2 v|fk (θ, ϕ)|2 dΩ
Definition 3.3 (Differentieller Wirkungsquerschnitt). Man nennt
dσ
|A|2 v|fk (θ, ϕ)|2
=
= |fk (θ, ϕ)|2
dΩ
|jein |
den differentiellen Wirkungsquerschnitt.
Der Niederenergie-Grenzfall k → 0 definiert die Streulänge
(3.18)
(3.19)
a = lim fk
k→0
3.6. Schrödinger-Gleichung als Integralgleichung, Greensche
Funktionen
Betrachtet werde nun die inhomogene Wellengleichung
(3.20)
∆ + k 2 ψ(k, r) = U (r)ψ(k, r)
und deren äquivalente Darstellung als Integralgleichung
Z
(+)
(+)
+
(3.21)
ψ (k, r) = φk (r) + d3 r0 G0 (k; r, r 0 )U (r 0 )ψ (+) (k, r 0 )
3.6. Schrödinger-Gleichung als Integralgleichung, Greensche Funktionen
31
(Lippmann-Schwinger-Gleichung) mit den Randbedingungen
∆ + k 2 φk (r) = 0
und
(+)
φk (r) = eik·r
(Lösung der homogenen Wellengleichung mit Randbedingung).
Wie man sieht enthält die partikuläre Lösung der inhomogenen Glei(+)
chung die Greensche Funktion G0 , die die Differentialgleichung
(+)
(3.22)
∆r + k 2 G0 (k; r, r 0 ) = δ 3 (r − r 0 )
mit Randbedingung einer auslaufenden Kugelwelle für r → ∞ erfüllt.
Für r 6= r 0 erhält man leicht
(3.23)
(+)
G0 (k; r, r 0 )
0
eik|r−r |
=−
4π|r − r 0 |
An der Stelle r = r 0 ist 3.22 singulär. Auflösen liefert
(3.24)
(+)
∇r G 0
= δ 3 (r − r 0 )
| {z }
Daher reicht es, an der Stelle
(3.25)
(+)
−k 2 G0
| {z }
dominiert unwesentlich bei r=r 0
r = r 0 die Differentialgleichung
(+)
∆r G0 (r − r 0 ) = δ 3 (r − r 0 )
zu betrachten mit der bekannten Lösung
(3.26)
(+)
G0 (r − r 0 ) = −
1
4π|r − r 0 |
Damit ist die Lösung von 3.21
Z
ik|r−r 0 |
(+)
ik·r
3 0 e
(3.27)
ψ (k, r) = e
− d r
U (r 0 )ψ (+) (k, r 0 )
4π|r − r 0 |
Untersucht werde nun das asymptotische Verhalten von ψ (+) (k, r). Entwickelt man für r r0
r
p
r · r 0 r02
r · r0
0
k|r − r | = k r2 − 2r · r 0 + r02 = kr 1 − 2 2 + 2 ≈ kr(1 − 2 )
r
r
r
0 r
0
0
= kr − kr · = kr − k · r
r
so ist
Z
eikr
0 0
(+)
ik·r
(3.28)
ψ (k, r) ≈ e
−
d3 r0 e−ik ·r U (r 0 )ψ (+) (k, r 0 )
4πr
Vergleich mit der asymptotischen Form der Streulösung 3.10
ψ (+) (k, r) = eik·r +
eikr
fk (θ, ϕ)
r
32
3. Streuung
liefert die Streuamplitude
Z
1
0
d3 r e−ik ·r U (r)ψ (+) (k, r)
4π
Z
m
0
=−
d3 r e−ik ·r V (r)ψ (+) (k, r)
2π~2
d*r
,\
G
N
tt-
S.'
{_
{
s\
\
ll
S
C\
so
tl
td-'o)
t}l
\
a\
-1.\
*l tt
sl F
I
Betrachtet man den Spezialfall der Streuung an einem Zentralpotential
V (r) = V (r) mit r = |r|, kann die Integration teilweise direkt durchgeführt
N
u)
,t'uI -\-v
iU\
+
Tle
r{
a
t5
e(
\'q
Die Bornsche Streuamplitude lässt sich nun schreiben in der Form
Z
m
(3.32)
fBorn (θ) = −
d3 r e−iq·r V (r)
2π~2
t-v'
$
,1
I
t{
θ
2
$t
:$t<
N)F
s\ {!
J{t-r
?. -9.
rl
shr
d l$,
T, \ J t- fc'-* *l;s
{
t+
q
.?l
ts-
r
q = 2k sin
r -l ,
t
t
\(
J\
ts-.
t
I z
sr+
tl- \
tfl
!\l
F>
q x'
\
θ
2
also
(3.31)
a-R*
\4
\I
()v
r r, $
i',
Der auf das Streuzentrum übertragene Impuls ist ~q mit q = k0 − k. Es
a)
L
q
rd
\
: *v rs-- d' L-R
r.,F
i-t
r\
$ss
(jll
\r! 3
J
*,43
hL-F\
Die Streuamplitude ist in dieser Näherung (Bornsche Näherung) also proportional zur Fourier-Transformierten des Streupotentials.
q 2 = k2 + k02 − 2k · k0 = 2k 2 (1 − cos θ) = 4k 2 sin2
U
\
rl
I
tr
o
d
$
\q
Ist das Potential |V | E, ist Störungstheorie 1. Ordnung im Potential
V anwendbar. Dies führt effektiv zur Ersetzung ψ (+) (k, r) → eik·r . Die
Streuamplitude 3.29 geht dann über in
Z
m
0
d3 r ei(k−k )·r V (r)
(3.30)
fBorn (θ, ϕ) = −
2
2π~
gilt
Y
#
-t
r+
tt
TL
f-l
4
N+
-lq
D sli
3.7. Bornsche Näherung
il oi9
ql *l
ll-31 $"k {n
$l .l=$
ql
frr
N0
lr)
fk (θ, ϕ) = −
^\ *c
(3.29)
3.8. Beispiel: abgeschirmtes Coulomb-Potential/Yukawa-Potential
33
werden, indem man zu dreidimensionalen Polarkoordinaten übergeht
Z
Z
Z ∞
d3 r e−iq·r V (r) =
dr r2 dΩ e−iqr cos θ V (r)
0
Z 1
Z ∞
d cos θ e−iqr cos θ
dr r2 V (r)
= 2π
0
| −1
{z
}
=
4π
q
Z
2
1
[e−iqr −eiqr ]= qr
−iqr
sin qr
∞
dr r sin qrV (r)
0
Für die Streuamplitude bleibt in diesem Fall nur das r-Integral zu lösen
Z
2m ∞
dr r sin qrV (r)
(3.33)
fBorn (θ) = − 2
~ q 0
3.8. Beispiel: abgeschirmtes
Coulomb-Potential/Yukawa-Potential
Definition 3.4 (Yukawa-Potential). Ein Yukawa-Potential ist ein abgeschirmtes Coulomb-Potential von der Form
(3.34)
V (r) = g
e−µr
r
Die Streuamplitude ergibt sich für ein solches Potential nach 3.30 in
Bornscher Näherung die Streuamplitude zu1
Z
e−µr
2m
g
2mg ∞
dr r sin(qr)
(3.35)
=− 2 2
fBorn (θ) = − 2
~ q 0
r
~ q + µ2
und damit ist der differentielle Wirkungsquerschnitt
(3.36)
g4
dσ
4m2
= |f (θ)|2 = 4
dΩ
~ (q 2 + µ2 )2
mit q 2 = 4k 2 sin2 2θ .
Coulomb-Potential (z.B. Elektron-Proton-Streuung). In einem ersten Schritt kann man das Coulomb-Potential
(3.37)
V (r) = −
e2
r
1dabei wurde verwendet
Z
Z
e−µr
4π ∞
4π
d3 r e−iq·r
=
dr sin(qr)e−µr = 2
r
q 0
q + µ2
34
3. Streuung
als Grenzfall µ → 0 eines Yukawa-Potentials betrachten (g = −e2 ). Aus
3.35 und 3.36 erhält man dann sofort
(3.38)
fBorn (θ) =
2m e2
~2 q 2
und
(3.39)
dσ
4m2 e4 m 2
= 4 4 =
dΩ
~ q
2
bei fester Energie E =
~2 k2
2m ,
e
~k sin 2θ
also insgesamt
e4
dσ
=
dΩ
(4E)2 sin4
(3.40)
!4
θ
2
Bei der Interpretations dieses Ergebnisses für kleine Streuwinkel (v.a. Vorwärtsstreuung θ → 0) ist jedoch Vorsicht geboten, da im Rahmen der Herleitung
ein Potential ∝ 1/r explizit nicht behandelt werden kann und gesonderte
Methoden benötigt.
3.9. Die Partialwellenmethode
3.9.1. Vorbereitung. Betrachtet werden soll nun die Streuung eines spinlosen Teilchens an einem Zentralpotential V (r) (ohne weitere Einschränkungen). Dieses Problem beschreibt man am Besten mit dem Hamilton-Operator
~2 1 ∂
L2
2 ∂
(3.41)
H=−
r
− 2 2 + V (r)
2m r2 ∂r
∂r
~ r
in Polarkoordinaten. Dabei ist
L = −i~r × ∇
(3.42)
der Bahndrehimpulsoperator. Es gilt [H, L2 ] = 0 = [H, Lz ], damit besitzen
der Hamilton-Operator und L2 bzw Lz gemeinsame Eigenfunktionen (die
sog. Kugelfunktionen)
L2 Y`m` (θ, ϕ) = ~2 `(` + 1)Y`m` (θ, ϕ)
Lz Y`m` (θ, ϕ) = ~m` Y`m` (θ, ϕ)
Die Entwicklung der Streuwellenfunktion nach Kugelfunktionen hat dann
allgemein die Form
(3.43)
Ψ(+) (k, r) =
∞ X̀
X
`=0 m` =−`
(+)
c`m` R` (k, r)Y`m` (θ, ϕ)
35
3.9. Die Partialwellenmethode
q
. Dabei wurde zugleich eine Separation von Radialmit k = kez , k = 2mE
~2
und Winkelanteil der Streuwellenfunktion angesetzt. Für die radiale Schrödinger-Gleichung erhält man
~2 1 d
`(` + 1)
2 d
(3.44) −
r
−
R` (k, r) = [E − V (r)] R` (k, r)
2m r2 dr
dr
r2
beziehungssweise mit den Ersetzungen u` (r) = rR` (r) und U (r) =
2
d
`(`
+ 1)
s_
2
/6
(3.45)
+k −
− U (r) u` (r) = 0
dr2
r2
TH oO e
o T.Z.-z+.Q,^nt-'*-f
E'6^4eht
&nt:/Fl.
ro4<-_o-
.
772-./.o* Cla-
(r)
:
Führt man zusätzlich die dimensionslose
(x) = u`x(x)
rtw Variable x = kr und F`")
ein, erhält
man )<aus 3.45
wechselwirkungsfreie
Teilchen (V = 0) die Beskrfür in"C(.U)
se#e2 T,k):
+
selsche Differentialgleichung
2
f -lz
2 d
`(` + 1)
d
+
+ 1−
F` (x) = 0
(3.46)
2
dr
x dx
x2
q>/tr, +** +(z:o
ry')-J6&)
Lösungen der Besselschen Differentialgleichung 3.46 sind in Tabelle 3.1
b;
*"
C9.,r*1s.^14dargestellt.
ft* e--^ 7jt h-"o4re )
*\,rcf1
a
WC"1 A-'U
( rt !:'*'=
EV'*')
4
u4-&
2m
V
~2
Lx ,
16^r(o'?)
-tWufutrtltN-W{
#nrn=u
Bessel-Funktionen
j"` (x)&TSCr.LNeumann-Funktionen n` (x)
-'r
sin x ,-,
j0 (x) = x
n0 (x) = − cosx x ryr. (*
(furxt)
)
x
x
x
j1 (x) = sin
− cos x
n1 (x) = − cos
− sin
x
x2 \---i x
x2
S' tr )< 3
3
3
x − x2 cos x n2 (x) = − +),
− x1 cos
j2 (x) = x33 −: x1 sin
s x − x9"-ft
2 sin x
x2 (x)
)<
X
.. ;loC*l
..
.
.
^
CD$
x
$.'r.
X
eo
..fin x
JX
t><)
vto
1 d `- cos x
` −(x):
` −s1 d ` sin x
, x
n
(x)
=
−x
j` (x)J=
52
`
.K
)<
x dx
x
x dx
x
,/\
f z - Lösungen
a'.
;'
-:- t-Cir,,,
der
7 67Jx Differentialgleichung
) : | 3.1.
=x - Besselschen
nz(x) =--l'+
7 > ( xTabelle
-* , t \
t< /
\><3
72
\ )<3
=
-x ,,(f t-d
(-Fdx/
x ( [ / d\e
(-*e1-
*4
lceJx
* + r,'.r
21L-
4pk)
,l'n (x) =
d<
"/
l?*r*
l<
*9irar
XI
-h;--
(f:
t{"a-'^
kzu)
de-, --L-,
oDiez^*xJ/H
(sphärischen) Bessel-Funktionen
treten
in der Entwicklung
der ebe-
( o.l
nen Welle (k = kez ) nach Kugelfunktionen auf:
-+\
r -
il<'r
:e'
ikz
&
i*
?t< = - Re ,
G) = Qn/fr)VG)
-l=o
.: e.
ikr
ces O
;t Cz!+L)
Jnkv)
P (c"< e1
36
3. Streuung
(3.47)
e
ik·r
=e
ikz
ikr cos θ
=e
=
∞
X
i` (2` + 1)j` (kr)P` (cos θ)
`=0
Dabei
sind die Legendre-Polynome gerade gegeben durch Y`,0 (θ, ϕ) =
q
2`+1
4π P` (cos θ).
Für die weitere Diskussion sind bestimmte Linearkombinationen der
Bessel- und Neumann-Funktionen von großer Bedeutung, die sog. Hankel-Funktionen
(1)
h` (x) = h+
` (x) = j` (x) + in` (x)
(2)
h` (x) = h−
` (x) = j` (x) − in` (x)
Die h±
` (kr) verhalten sich wie auslaufende bzw. einlaufende Kugelwellen,
z.B.
cos(kr)
eikr
sin(kr)
−
i
=
−i
h+
(kr)
=
j
(kr)
+
in
(kr)
=
0
0
0
kr
kr
r
Das asymptotische Verhalten der Bessel-, Neumann- und HankelFunktionen ist
`π
x→∞ 1
j` (x) −→ sin x −
x
2
1
`π
x→∞
n` (x) −→ − cos x −
x
2
ix
i i(x− `π )
x→∞
`+1 e
2
h+
(x)
−→
−
e
=
(−i)
`
x
x
−ix
`π
i
e
x→∞
−i(x− 2 )
h−
= i`+1
` (x) −→ x e
x
3.9.2. Partialwellen, Streuamplituden und Streuphasen. Das Potential V0 besitze nun eine Reichweite R0 . Betrachtet man die Lösung der
Schrödingergleichung mit der Randbedingung auslaufender Kugelwellen,
so gilt für r > R0 folgende Entwicklung:
i
Xh
(+)
ψ (+) (k, r) =
i` (2` + 1)j` (kr) + c` (k)h` (kr) P` (cos θ)
`
Mit j` (kr) =
1
2
h
i
(+)
(−)
h` (kr) + h` (kr) und c` (k) =
ψ (+) (k, r) =
X i`
`
für r > R0 .
2
i`
2 (2`
+ 1)a` (k) folgt
h
i
(−)
(+)
(2` + 1) h` (kr) + (1 + a` (k))h` (kr) P` (cos θ)
Die Größe S` (k) := 1 + a` (k) nennt man S-Matrix. Stromerhaltung
besagt, dass der Strom divergenzfrei ist
1
,1,'*,
ci,;1 Ju
{ A!*)[-li-'c*"t+ (t* art*t)./,[.Lo,,)
7
?Y
?nGe<e1
.
ank-
.
k"
G;/k
2z
s --l-zarrerx
sr Ctr): 7-+ a"Ckl -/-*/f
37
3.9. Die Partialwellenmethode
.
)
.w
a&- $."^
6e4-ft:
=Wro^u/e*.4
,\
d*u1u.nfu"v I
:
/*
x)
'^
Y-" "=
r/
t
\.
J*a
arr-, (o^f
u
-ab4
I die Summe der radial ein- und auslaufenden Ströme jr = j· r
n - ' . und damit
=
bf22',\\+ |r|
2*"+
1re-rJ*4'ou"/e*.
1n
7 i
y'
verschwinden
/F/impliziert
J' muss. Dies
dffl*a -
t g::
n
-- --u
e-Y, - "u*a/
n
*r<r. .n^a oiurr 4V
t
|S` | = |1 + a` | = 1
-l
lt*qel:
/S* l:
x
5--,
oder äquivaltent S`∗ S` = 1 (Unitaritätsbedingung). Also erfüllt S` (k) die
Darstellung
a
o. @'7$-o"tQ
'|v'+
S` (k) = e
`
mit den reellen Streuphasen δ` (k). Es gilt
{ee'7
<{fr{.(t oLu-=bot'
T
r-p
Snct
iδ (k)
(3.49)
a (k) = 2ie
sin δ (k)
`
`
p"<,.-l-l- .
]*'ct,J7O,
(kn^^*(.;{;6b.4"^J7)
2iδ (k)
odt'
= i(3.48) S;Se
`
(A)die
: asymptotische
u2n'61ck)Form von ψ(+) (k, r) mit
Vergleicht man
S{ nun
eikr
ψ (+) (k, r) −→
eikz + f (θ) n* (r
→ ∞) Col
evt
aee*' ReettEp
lr*euPn
t
r
,)re
'o'
die Partialwellen-Entwicklung der Streuamplitude bestimmen:
= lie''dg {-,t
+lässt sicha"&)
Qcol
X
ψ (+) (k, r) −→ eikz +
`
i`
eikr
(2` + 1) a` (−i)`+1
P` (cos θ)
2
kr
Es folgt durch direkten Vergleich
1 X
f (θ) =
(2` + 1)a` (k)P` (cos θ)
2ik
`
oder
(3.50)
f (θ) =
X
(2` + 1)f` (k)Pl (cos θ)
`
mit
(3.51)
f` (k) =
1 iδ`
e sin δ`
k
Die f` heißen Partialwellen-Streuamplituden.
(r → ∞)
38
3. Streuung
3.9.3. Interpretation der Streuphasen. Nun zurück zur Streuwellenfunktion:
X
(+)
ψ (+) (k, r) =
i`3-2o
(2` + 1)R` (r)P` (cos θ)
`
--( * e-C(o^
{e*(u-" lautet die Radialwellenfunktion
Außerhalb?.4
des Potentialbereichs
4ar4
ct4)i
ct")+ {co t-t'f'
: * 1t Ih (−)
{-:"h
R;'R(+)
(+)
l-'
=
h
(kr)
+
S
(k)h
(kr)
`
`
`
2 `
h
iδ
+
ckdJi
t'kr
e ` −iδ` (−)
: *
iδ` (+)
u
[= "-'44-'[k,1
e
h
(kr)
+
e
h
zrrl
"n'\nJ;-'
{I
`
` (kr)
2
ite f ei(*"
i
-i&" - `π
iδ` h- g- t,`π)
e
EN - QvT-wtcKtuatq
i(kr− 2 +δe_
−i(kr− 2 +δ` )
+La{ELL
*
`)
lee
−
e
−→
L
z'tao
2;kr
2ikr
iδ
- 4 o ot
e `
`π
- e
= slnCkr-&*Jn)
sin(kr −
+ δ` )
,'z
kr
2
,r,2+toikkr
e
(z&t)T qz /
a
b*ArJ
.h\
'2
-V-q
<'
Fi)
k-.^-A,
kr Den Unterschied
-r(freie Lösung)
fzurULösung
o/rV ohne
u.c41 .o/ru<
/il
or,,^Y Wechselwirkungspotential
dlr
o V?2Vtzo,
^xPr,
rzGH o)
-{
v
,p-4/"he#-^#-l1 Cfr-e /a'1.`π--+v/ I
7nfuaQarL
(0)
L kr −
R` (r) =rlj` (kr) −→
sin
2
(k,-bt
* kr
n1kl ?o Cceae1
1
f"'o)
fi',crt:
* 3,1'
)4(*,,
pc<
?eCceae)
P^flt.Zr*lP.
qrunZ=o CS --rt&l
,,8,
tt k) : ,p1=oG)
-n'Q"*+
/
[,,\"
!LLEN - kn^ o* fr^h&ro-
*"^
"Fu' i*ic*j
t
i
eb-k*
_1
" voUt'
?"4"*,*",1
R/*'crt Pa cc+ae1
4'<"k
z--1
veranschaulicht folgendes Beispiel der s-Wellen Streuung (Partialwelle mit
*[7a-a.^tc4
l = 0):
ar-.6-a,
tsr
S+:t
U ^., -Cr\'(k""4)
itfc"1
oQY
Ltb) ,u aYnt"
%vyhr.,>&
>o
' afla/<-?;
q
1o:
w_&
3.9.4. Berechnung der Partialwellen-Streuamplituden. Betrachtet man
wieder den exakten Ausdruck der Streuamplitude 3.29
Z
m
0
fk (θ, ϕ) = −
d3 r e−ik ·r V (r)ψ (+) (k, r)
2
2π~
39
3.9. Die Partialwellenmethode
0
und entwickelt e−ik ·r und ψ (+) (k, r) nach Kugelfunktionen bzw. Partialwellen, so sieht man
Z ∞
2m X
(+)
(2` + 1)P` (cos θ)
dr r2 V (r)j` (kr)R` (r)
f (θ) = − 2
~
0
`
und findet:
1
2m
f` (k) = eiδ` sin δ` = − 2
k
~
(3.52)
hl
u a--"F
f>'dq
0
(+)
dr r2 V (r)j` (kr)R` (r)
(+)
eu:"y r: X
;5c
Vr"^*-ev
2
Eine wichtige Abschätzung3 - 2zur
Partialwellenentwicklung ist die Frage,
2 k2
2&' o< Lftruet,
. 41n/;It
r- /r;ul,E t = ~2m
wie viele Partialwellen
bei Y+
vorgegebener
Energie
und bei einem
Potential V mit
endlicher
Reichweite
r
zur
Streuamplitude
beitragen.
0 *?^
Arr'o-tft (- ?o4'o-(ue%^
+
bo-. 1.-rr-/R?
fu
a?:*r
hl
f>'dq
{fC! u a--"F
LEN -
∞
Für ein “schwaches” Potential (|V | E) kann man R` ≈ j` (kr) und
f` = k1 eiδ` sin δ` ≈ δk` setzen und erhält damit eine Bornsche Näherung für
die `-te Partialwelle
Z
2mk ∞
δ` ≈ − 2
dr r2 V (r) [j` (kr)]2
~
0
Diese verhalten sich für kleine k (k → ∞) wie
Z
2mk ∞
δ0 −→ − 2 3 - 2 2 dr r2 V (r) = −ka
~
0
o< Lftruet,r- /r;ul, t
Y+ 2&'
mit der .Streul
änge
41n/;It
Z
2m ∞
= 2
dr r2 V (r)
Arr'o-tft (- a?o4'o-(ue%^
*?^
+
bo-. 1.-rr-/R~ 0
3- 2L
ot,,-i
Z
6.'
fu
eu:"y r: X
;5c
Vr"^*-ev
6.' ?
l^
c*eo) I dr
,-Wy)rkqPnuC,
l^
3 Cc*eo) I dr
2ekt)
,-Wy)rkqPnuC,
3n
s
e-"
",u;n
Pr'*'{'sPr'*'{'s
G)-ln&v;
7, r-TG)-ln&v;
b ein: Potential
A(-f-'*( mit endlicher #re.^.e--gt*
J@p**d+,
Abbildung
3.1. Beispiel für
Reichweite und
44
#re.^.e--gt*
: A(-f-'*(
Illustration
des Streuparameters
b
J@p**d+,
.uE{. bdz-r
Z_ 4-/" Oo .
44
V>r-f**
V>r-f**
.uE{. dz-r Z_ - 4-/"
Oo .
>
-t
: -itn
->
-t
w) : des
-*Fstreuenden
fb,
- - t i.e.
: r der
Ein Maß
ist der Streuparameter
+dafür
: Abstand
Ltr*
w)
-*F3
L :L -itn Ltr*
>*-L,^p,^A
+ >*-L,^p,^A
T f
Teilchens von der z-Achse. Bekannterweise ist der Drehimpuls L̂ = −i~[r ×
,tt-*gttlu-n? /*/* Y-zz"l*^
,tt-*gttlu-n?
' ( /V <' (E /V I <' E
Y-zz"l*^
fürA Teilchen
auf einer Trajektorie mit
) ∇] = r × p̂. Eine gute Abschätzung
I
AH"2fa"t_
e
&al Pl"-'=1u'e
)
H"2fa"t_
L.'
(kr) ck44 Streuparameter
or&
Y
b
ist
d,"k,*-(w
jn
R;")
L.'
-tnfue'or& d,"k,*-(w
Y jn (kr) ck44
I
I
( '-l ∼
k'Lkb
(
Keine Streuung findet statt für b &'-r0 k'L
und die maximale Partialwelle ist
(- *
U aL,<.q Jv;f"ryeI>
daher
hn^>.*b
k*--v
z To ct)
Ue-:
#,
U aL,<.-
yk
(-
*
(3.53)
v"''J' [ip(kil" )
,-VGt
l'**, )^
[ip(kil" )
ry[**,v"vG):
W..
v"''J'
VGt
frz
zLA'tu6e
G):
kq
Jo
q - 1ry Jf^o,
r.VG1
o
fr>
kq
:r
v'a
cwteutcu-t*-(zeI>
lmax ∼#,kr
: 0 b z To
hn^>.*-k*--vU?,,bL.-
cwteutcu-t*-(z- (**r
irdv
f--t
,;i> 2r.r-
v'a
'\-' ka,
U?,,bL.-
ttttUrT
P"f{v/qt-Ar*
(**r
n
( S kn
P"f{v/qt-Ar*
L e-'
ct)
:
'\-'u^-f>*'A%
ka,
dK,** ft' A.-L fi u g-J*,"kA
,;i> 2r.r-
3
u^-f>*'A%
obq
obq
40
3. Streuung
Zur Partialwellenentwicklung der Streuamplitude tragen also Bahndrehimpulse mit
l . kr0
bei.
3.10. Das optische Theorem
Das optische Theorem liefert einen wichtigen
Zusammenhang zwischen dem
R
dσ
totalen Wirkungsquerschnitt σtot = dΩ dΩ
und dem Imaginärteil der
elastischen Vorwärts-Streuamplitude Im f (θ = 0). Es ist
f (θ) =
1X
(2` + 1)eiδ` sin δ` P` (cos θ)
k
`
und
dσ
= |f (θ)|2
dΩ
1 X
= 2
(2` + 1)(2`0 + 1)ei(δ` −δ`0 ) sin δ` sin δ`0 P` (cos θ)P`0 (cos θ)
k
0
`,`
Damit ergibt sich
σtot = 2π
Z
+1
−1
d cos θ
dσ
dΩ
unter Verwendung der Orthogonalität der Legendre-Polynome
Z +1
2
d cos θ P` (cos θ)P`0 (cos θ) =
δ``0
2` + 1
−1
(3.54)
σtot (k) =
4π X
(2` + 1) sin2 δ` (k)
k2
`
Andererseits ist
Im f (θ = 0) =
h
i 1X
1X
(2` + 1)Im eiδ` sin δ` =
(2` + 1) sin2 δ`
k
k
`
`
Dies liefert sofort
Satz 3.5 (Optisches Theorem).
(3.55)
σtot (k) =
4π
Im f (θ = 0, k)
k
41
3.11. Resonanzen
3.11. Resonanzen
Der totale Wirkungsquerschnitt
3-23
z+
3-
3*
4π X
(2` + 1) sin2 δ` (k)
σtot = 2
V=A^)ANZeu
k
44
`
9-)': "/'*
R k ufu 6-'f Q.ct !R'lCU tv r T TL*"f
'--4"e1
1
hat Maxima bei δ` = (n :+
)π (n =(z0, 1, 2,-e,r
. . . ). Dort ist die Partialwellen-2+vk e,1 L4 r4l
-/.
"4nt
kz-Es( gilt:
Streuamplitude
rein imaginär.
olu-,
u^^4 ry;u;'{e
- #
-64. f,e : (* * *) o
G = o, 4, zr..-/
/,t# -[ao t lr*.-o-1 iδ`
1
tan
δ
Uo uoO R W - k" - o',-O*L*^ot'-,
`
( ta&o-* - J&=,-.
^*
sin δ` =
dYt'= d'u-e ?.aro
9e. f+` (k)
k
k 1 − i tan δ` fr''l.^r{q
Fc
L\g\f,
rf
VYI
2 n t-anP
.
fe-L
V
(ze+4.nuQ<rdeP" Cwte)
tan δ` durchläuft Polstellen bei ;iln
δ` = (n + 21 )π. In der Nähe der Pole kann
7
Qtt &
'n\A:
g
f rLk'l ' =
man daher die Tangensfunktion
parametrisieren durch
/(
k
- 4rc.-h 0e
-=
2
2
Γ` (E)/2 ?"Z,tk^Ck^~ b,kzn^
'u'-''4e;*-ft
(*e1
to-.
A
,
E=
tan δ` =
}r'nbto1Q,
)b!*r)JGe-&?,,0",
E
−?q--=**-.r''>i
ER
qr<- 2m
:
(ryr*
,
n2r)
d(
-Ven*'--'*t.-:
4a- v
l|(et/z- als
Damit lässt sich die Streuamplitude
schreiben
/
\-.
ir- oLu C(,n' % {z'q
*3.-, o d 6 o
CIn
T@h
'
r
L
_R
o&-r7o t..
or*o c@4
1
Γ
(E)/2
=
q
`
qA' G"" (3.56)
nn
f` (k) =
ho 4r,
^.
k
E
−
E
− iΓ` (E)/2
fiGt/z
R
+
'l
!
I
f)
f t
t
\
\\'tn
w(
ry't\
t
(==+)
\
L
nla"l.
E-ER.-1QG)/z_
-sin-4r,(Breit-Wigner-Resonanzamplitude)
CeerT---rn Gru!B i
=oS:
IL
t
K
:lL
k
z
(
e
Q!+t;
!
Ln"
f
/e
.-+
(ze* t1 Sr'r.
'4",,
4J
a
P"4" u at4JVa----p4l--,-l<
kfe
s-
n'-
"1
T
\-/
/ t',sove-,'< .
5^f
) : 3"k
@=o,k1
Der Beitrag einer Resonanz in einer Partialwelle zum totalen Wirkungsquerschnitt ist
X
4π
σtot =
σ` , σ` =
(2` + 1)Im f` (k)
k
`
Einsetzen der Breit-Wigner-Resonanzamplitude 3.56 liefert die BreitWigner-Formel
(3.57)
σ` (E) =
Γ2`
(2` + 1)π
k2
(E − ER )2 + Γ2` /4
42
3. Streuung
3.12. Inelastische Streuung
Bei der eben behandelten elastischen Streuung waren die Streuphasen δ`
reell. Im Fall der inelastischen Streuung gehen die mit Energie E einlaufenden Teilchen im Streuprozess “verloren”, entweder durch Energieverlust
(Anregung des Targets) oder durch Reaktionen. Bei gegebener Energie E
ist also |S` (E)| < 1. Daher kann man in diesem Fall die S-Matrix schreiben
als
S` = η` e2iδ` ,
0 ≤ η` ≤ 1
und die Partialwellen-Streuamplitude
1 2iδ`
η` e
−1
f` =
2ik
Man nennt η` den Inelastizitätsparameter.
3.13. Operator-Formalismus der Streutheorie
In diesem Kapitel werden beliebige Streu- und Reaktionsprozesse, nicht
beschränkt auf elastische Streuung, behandelt. Der Ausgangspunkt sind
vollständige Sätze von Zuständen |φn i mit
(En − H0 )|φn i = 0
(3.58)
(freie Schrödinger-Gleichung)
(+)
und |ψn i mit
(3.59)
(En − H0 − V )|ψn(+) i = 0
(mit Wechselwirkung)
beide mit der asymptotischen Randbedingung auslaufender Kugelwellen. Ist
~2
∆, so ist |φn i eine ebene Welle und φk (r) = hr|φn i =
zum Beispiel H0 = − 2m
ik·r
e
(n , k).
Die formale Lösung der vollen Schrödinger-Gleichung ist
(3.60)
|ψn(+) i = |φn i + [En − H0 + iε]−1 V |ψn(+) i
(Lippmann-Schwinger-Gleichung) und
|ψn(+) i = |φn i+
1
1
1
V |φn i+
V
V |φn i+. . .
En − H0 + iε
En − H0 + iε En − H0 + iε
G(+) (E) = (En − H0 + iε)−1 ist offenbar der Greensche Operator mit
der Randbedingung für auslaufende Kugelwellen (+iε am Pol). Es gilt
(E − H0 )G(+) = I (Einheitsoperator)
43
3.13. Operator-Formalismus der Streutheorie
In der Ortsdarstellung ist 3.60 die Gleichung für die Streuwellenfunktion
1
ψn(+) (r) = hr|ψn(+) i = φn (r) + hr|
V |ψn(+) i
En − H0 + iε
X
1
hr|
= φn (r) +
|φm ihφm |V |ψn(+) i
E
−
H
+
iε
n
0
m
X
φm (r)
= φn (r) +
hφm |V |ψn(+) i
E
−
E
+
iε
n
m
m
Definition 3.6 (T-Matrix). Man nennt
(3.61)
die T-Matrix.
Tmn = −hφm |V |ψn(+) i
Die Streuamplitude nimmt dann die Form
2M
fmn = −
Tmn
4π~2
an (Im Falle der elastischen Streuung identifiziere n ≡ k, m ≡ k).
Die früher eingeführte S-Matrix ist allgemein
Smn = δmn + 2πiδ(Em − En )Tmn
mit der Unitaritätsbedingung
S†nm Sml = δnl
bzw.
S† S = I
(Zur Erinnerung: es ist (S† )nm = (Smn )∗ ).
Das optische Theorem lässt sich in der Operator-Formulierung schreiben
als
Im Tnl =
X
m
πδ(En − Em )T†nm Tml
44
3. Streuung
Übungsaufgaben zu
Kapitel 3
Aufgabe 5
r→∞
Der asymptotische Ansatz ψ(r ) −→ ψ0 (r ) + ψS (r ) für die Wellenfunktion
eines Teilchens der Masse m, das an einem Zentralpotential V (|r |) gestreut
wird, setzt sich aus der einfallenden Welle
ψ0 (r ) = eikz = eikr cos θ
und der Streuwelle
ψS (r ) = f (θ)
eikr
r
zusammen.
(1) Zeigen Sie, dass dieser asymptotische Ansatz die Schrödingergleichung
2 k2
erfüllt, falls das Streupotential für r → ∞ schneller als 1r
mit E = ~2m
abfällt.
(2) Berechnen Sie die Stromdichte
~
(ψ ∗ ∇ψ − ψ∇ψ ∗ ) .
2mi
Hinweis: Der Gradient in Kugelkoordinaten lautet
j =
∇ = er
∂
1 ∂
1
∂
+ eθ
+ eϕ
.
∂r
r ∂θ
r sin θ ∂ϕ
Aufgabe 6
Gegeben sei ein kugelsymmetrisches Potential
V (r ) = gδ (3) (r )
mit einer Konstanten g.
a) Man zeige, dass die Streuamplitude in Born’scher Näherung gegeben ist
durch
m
f (θ) = −
g.
2π~2
b) Das Potential V (r ) werde nun verwendet, um die Streuung von thermischen Neutronen an Atomkernen zu simulieren und die Streulänge a zu
reproduzieren. Wie lautet der entsprechende Ausdruck für g? Welchen
Wert nimmt g für eine typische Streulänge von a = 5 fm an?
45
Übungsaufgaben zu Kapitel 3
Aufgabe 7
Ein Teilchen werde gestreut an einem kugelsymmetrischen Potential
V (r) =
g 2 −µr
e
r
mit Konstanten g und µ.
(1) Berechnen Sie die Streuamplitude in Born’scher Näherung.
(2) Man zeige, dass der daraus folgende differentielle Wirkungsquerschnitt
als Funktion des übertragenen Impulses ~q durch
2
dσ
2mg 2
=
dΩ
~2 (q 2 + µ2 )
gegeben ist.
(3) Man verwende dieses Resultat, um die Rutherford-Formel für die Streuung von α-Teilchen der Energie E an Kernen der Ladungszahl Z herzuleiten. Man zeige, dass der differentielle Wirkungsquerschnitt für diesen
Streuprozess als Funktion des Streuwinkels durch folgenden Ausdruck
gegeben ist:
2
dσ
Ze2
=
.
dΩ
2E sin2 (θ/2)
Aufgabe 8
Die Green-Funktion G(r − r 0 ) erfüllt die Gleichung
(∆r + k 2 )G(r − r 0 ) = δ (3) (r − r 0 ).
Zeigen Sie, dass durch
0
G(r − r ) =
i
(I+ + I− ) mit I± =
2
8π |r − r 0 |
I
C
0
eiq|r−r |
dq
.
q±k
für die beiden angegebenen Integrationswege C in der komplexen Ebene eine
Lösung dieser Gleichung gegeben ist. Werten Sie dazu die Integrale I+ und
I− durch Integration in der komplexen q-Ebene jeweils entlang der beiden
angegebenen Integrationswege C+ und C− mit Hilfe des Residuensatzes aus.
Im q
Im q
C
C
+
Re q
−k
+k
−
Re q
−k
+k
46
3. Streuung
Interpretieren Sie die zwei Lösungen im Hinblick auf ihr asymptotisches Verhalten. Welcher Zusammenhang besteht zwischen den gewählten Integrationswegen und der für Streuprobleme relevanten physikalischen Randbedingung?
Aufgabe 9
Berechnen Sie die differentiellen Wirkungsquerschnitte in Bornscher Näherung für die folgenden Potentiale:
(1) V (r) =
(2) V (r) =
(3) V (r) =
g 2 −µr
r e
2 2
V0 e−µ r
V0 e−µr .
Aufgabe 10
Man untersuche die s-Wellenstreuung an einem kugelsymmetrischen Potential mit Radius R,
V0 > 0 . . . r < R
V (r) =
0
... r ≥ R
für den Fall mit Energie E < V0 .
(1) Zeigen Sie, dass die radiale Schrödingergleichung für die reduzierte sWellenfunktion (l = 0) u(r) = rψl=0 (r ) lautet:
2
d
2
+ q u(r) = 0.
dr2
Bestimmen Sie q 2 für r ≥ R und r < R.
(2) Begründen Sie den Lösungsansatz
u< (r) = c< sinh(pr)
für r ≤ R und
u> (r) = c> sin(kr + δ0 ) für r > R.
(3) Unter Verwendung der logarithmischen Ableitung von u(r) formuliere
man die Anschlussbedingung bei r = R und zeige, dass für die Streuphase δ0 gilt:
k
δ0 = arctan
tanh(pR) − kR.
p
(4) Bestimmen Sie das Verhalten der Streuphase für kleine Energien E =
~2 k2
2m . Zeigen Sie, dass für die Streuphase in diesem Grenzfall Folgendes
gilt:
k
δ0 ' tanh(pR) − kR + nπ.
p
Übungsaufgaben zu Kapitel 3
47
(5) Drücken Sie die Streuphase δ0 bei kleinen Energien durch die s-Wellenstreulänge
tanh(pR)
a0 ≡ R 1 −
pR
aus. Zeigen Sie, dass der Wirkungsquerschnitt für die s-Wellenstreuung
sich ergibt zu σ0 ' 4πa20 .
(6) Diskutieren Sie den Fall der Streuung an einer harten Kugel (V0 → ∞).
Geben Sie eine geometrische Interpretation des Wirkungsquerschnitts.
Aufgabe 11
Für die Streuung an einem kurzreichweitigen Potential verifiziere man, dass
die Wellenfunktion
i eikr
ψ(r ) = ψ(r, θ) = 1 +
cos θ
kr
r
ausserhalb der Reichweite des Potentials eine auslaufende p-Welle (` = 1)
darstellt.
Aufgabe 12
Ein Teilchenstrahl, dargestellt durch eine ebene Welle eikz , wird an einer
undurchdringbaren (harten) Kugel mit Radius R gestreut, wobei kR 1. Unter Berücksichtigung der s-Wellen-(` = 0)- und p-Wellen-(` = 1)Komponenten der gestreuten Wellenfunktion zeige man, dass der differentielle Wirkungsquerschnitt bis zur Ordnung (kR)2 dargestellt wird durch
dσ
1
2
2
2
= R 1 − (kR) + 2(kR) cos θ .
dΩ
3
Hinweis: Der Mittelwert von cos2 θ, gemittelt über alle Richtungen, ist 13 .
Aufgabe 13
Bei der Entwicklung der Streuamplitude
X
f (θ) =
(2` + 1)f` (k)P` (cos θ)
`
sind die Partialwellenamplituden in Anwesenheit von inelastischen oder Absorptionsprozessen gegeben durch
1 2iδ`
f` (k) =
η` e
−1
2ik
mit η` < 1.
48
3. Streuung
(1) Berechnen Sie den elastischen Wirkungsquerschnitt
Z
σel = dΩ |f (θ)|2 .
(2) Der gesamte Wirkungsquerschnitt der inelastischen Streuung ist
π X
σinel =
(2` + 1)(1 − η`2 ).
k2
`
Zeigen Sie, dass der totale Wirkungsquerschnitt gegeben ist durch
2π X
(2` + 1)(1 − η` cos 2δ` ).
σtot = σel + σinel = 2
k
`
(3) Man zeige, dass auch bei Präsenz von inelastischen Prozessen das optische Theorem
4π
σtot =
Im f (θ = 0)
k
gilt.
(4) Für maximal inelastische Streuung mit η` = 0 bestimme man σel und
σinel . Interpretieren Sie das Ergebnis.
(5) Man stelle den Verlauf der Partialwellenstreuamplituden f` (k) als Funktion von k im sogenannten Argand-Diagramm (siehe Abb.) in der komplexen Ebene dar.
0
1
0
1
0
1
0
1
k Im f l (k)
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
k Re f l (k)
0
1
0
1
0
1
0
1
111111111111111111111111111111
000000000000000000000000000000
Zeigen Sie, dass in diesem Diagramm die Trajektorie von kf` (k) für
η` = 1 auf einem Kreis mit Radius 12 verläuft. Wie lassen sich in dieser
Darstellung die Streuphase δ` und der Inelastizitätsparameter η` ablesen? Wie stellt sich eine Resonanz im Argand-Diagramm dar? Hinweis:
Man zeige kf` = 2i − 2i η` e2iδ` .