Protokoll zum Anfngerpraktikum

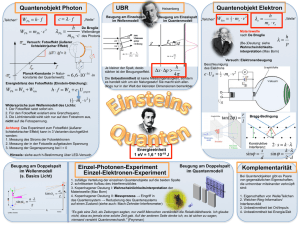
Protokoll zum Anfängerpraktikum
Beugung an periodischen und
zufälligen Strukturen
Gruppe 2, Team 5
Sebastian Korff
Frerich Max
29.05.06
Inhaltsverzeichnis
1. Einleitung
-3-
1.1 Allgemeines
-3-
1.2 Beugung am Doppelspalt
-3-
1.3 Beugung am optischen Gitter
-4-
2. Versuchsdurchführung
-5-
2.1 Beugung an einem Doppelspalt
-5-
2.2 Beugung an einem zweidimensionalen Transmissionsgitter
-6-
2.3 Beugung an einem eindimensionalen Transmissionsgitter
-7-
2.4 Beugung an zweidimensionalen Reflexionsgitter
-7-
2.4.1 Beugung am CCD-Target
-7-
2.4.2 Beugung an einer CD
-8-
2.4.3 Beugung an einer DVD
-8-
2.5 Beugung an Zufallsstrukturen
3. Beantwortung der Fragen
-9-10-
Literaturverzeichnis
Anhang
2
1. Einleitung
1.1 Allgemeines
Die Beugung oder Diffraktion ist die „Ablenkung“ von Wellen (wie Licht- und anderen
elektromagnetischen Wellen, Wasser- oder Schallwellen) an einem Hindernis. Bei
Beugungserscheinungen kann sich die Welle im geometrischen Schattenraum des
Hindernisses (Spalt, Gitter, Fangspiegel usw.) ausbreiten. Zur Beugung kommt es
durch die Entstehung neuer Wellen entlang der Wellenfront gemäß dem
Huygens’schen
Prinzip.
Diese
führen
durch
Überlagerung
zu
Interferenz-
Erscheinungen.
1.2 Beugung am Doppelspalt
Beim Doppelspaltexperiment lässt man kohärentes, monochromatisches Licht auf
eine Blende mit zwei schmalen Schlitzen fallen. Auf einem Beobachtungsschirm
hinter der Blende zeigt sich dann ein Interferenzmuster aus hellen und dunklen
Streifen. Dieses Muster entsteht durch Interferenz der Lichtwellen von den beiden
Blendenöffnungen.
Das Licht vom Spaltrand weist unter dem Winkel θ gegen das vom Zentrum
kommende Licht einen geometrisch feststellbaren Gangunterschied Δs =
wobei
d
d
sin α auf,
2
die Spaltbreite ist. Auslöschungen treten dann auf, wenn dieser
Gangunterschied Δs gerade ein ungerades Vielfaches der halben Wellenlänge
1
λ
2
ist. Es gilt für das m -te Minimum:
(1)
sin θ =
(2m − 1) ⋅ λ
2⋅d
, mit m = 1,2,3,...
m⋅λ
d
, mit m = 1,2,3,...
Für Maxima gilt:
(2)
sin θ =
Hinter dem Spalt erscheinen helle und dunkle Beugungsstreifen. Die Lichtintensität
nimmt mit wachsendem m stark ab. Für die Abstände u benachbarter Lichtmaxima
in Abhängigkeit des Beugungswinkels θ und der Brennweite f der abbildenden
Linse gilt:
(3)
u = f ⋅ tan θ
,für kleine Winkel: θ ≈
u
f
3
(a)
(b)
1 111
Abb.1: Interferenzmuster an einem (a) Einzelspalt und (b) Doppelspalt
Das Doppelspaltexperiment kann nicht nur mit Licht, sondern auch mit „Teilchen“
(Elektronen, Neutronen, Atomen, Fulleren-Molekülen usw.) durchgeführt werden. Es
zeigt sich auch in diesen Fällen ein Interferenzmuster wie bei Durchführung mit Licht.
Das bedeutet, dass auch klassische Teilchen unter bestimmten Bedingungen
Welleneigenschaften zeigen - man spricht dann von „Materiewellen“. Mit dem
Doppelspaltexperiment kann man so den Welle-Teilchen-Dualismus demonstrieren,
der nur im Rahmen der Quantenmechanik erklärt werden kann.
1.3 Beugung am optischen Gitter
Sind in regelmäßigen Abständen viele Spalte angeordnet, ergibt sich bei
Lichtbestrahlung eine Reihe von Beugungsreflexen, deren Anordnung derjenigen
entspricht, die man bei einem Doppelspalt mit dem gleichen Abstand erwartet. Mit
zunehmender Anzahl der Einzelspalte werden die Reflexe aber zu immer schärferen
Linien. Im Gegensatz zu den Spektren von Einzelspalt und Doppelspalt werden die
Hauptmaxima jedoch mit steigender Gitterkonstante schärfer abgebildet, die
Nebenmaxima
werden
zahlreicher,
aber
schwächer.
Somit
steigt
das
Auflösungsvermögen.
Da die Lage der Reflexe von der Wellenlänge des Lichtes abhängt, kann man
optische Gitter zur Trennung verschiedener Wellenlängen nutzen. Das ist im
Monochromator und bei der Spektroskopie der Fall. Es werden in der Praxis sehr
häufig regelmäßige Anordnungen von spiegelnden und nicht spiegelnden Streifen
als Reflexionsgitter verwendet. Die Rückseite einer CD wirkt ähnlich.
1
Halliday, David, u.a. : „Physik“, Wiley VCH, Weinheim, 2003, S. 1076
4
2. Versuchsdurchführung
2.1 Beugung an einem Doppelspalt
In diesem Versuch soll der Abstand d der Einzelspalte eines Doppelspaltes bestimmt
werden. Dafür wird paralleles Licht auf den Spalt geführt (siehe Abb.2).
Abb.2: Aufbau zur Vermessung von Beugungsbildern unterschiedlicher
Beugungsstrukturen BS. AW: Strahlaufweitungssystem, z.T. in Schutzkasten K, B: Irisblende, L:
Linse, S: (durchbohrter) Schirm, R: Graufilterrad, P: Polarisationsfilter, ZS: Zeilenselektor, DO:
Digital-Speicheroszilloskop, VS: Videosignal (an Buchse „FBAS IN“ von ZS), TS: Triggersignal
(an Buchse „TRIGGER SCOPE“ von ZS).
Die Aufnahme des Intensitätsverlaufs erfolgt mit einer CCD Kamera, die an einen
Fernseher angeschlossen ist. Eine Zeile des Fernsehbildes wurde mit Hilfe eines
Zeilenselektors isoliert und mit einem Digital-Speicheroszilloskop angezeigt. Dabei
wurde das Signal extern auf sich selbst getriggert. Um die Intensität zu regulieren und
damit genauere Graphen zu erhalten, wurde ein Polarisationsfilter vor der Kamera
eingesetzt. Um einen optimalen Verlauf der optischen Achse zu garantieren, wird mit
Hilfe des Zieltargets der Spalt genau in die Mitte des Strahls positioniert.
Gemessen wurde nun der zeitliche Abstand Δt zwischen dem 0. Maximum (der
optischen Achse) und den Minima n-ter Ordnung.
Die auf dem Oszilloskop dargestellte Bildinformation einer Zeile von 52µs entspricht
−3
einer Länge von (4,76 ± 0,02) ⋅ 10 m . Um die Zeiten in eine Länge umzurechnen,
benötigt man also einen Umrechnungsfaktor S t →s . Dieser ist folglich definiert als
S t →s
( 4,76 ± 0,02) ⋅ 10 −3 m
m
:=
= 91,538 ± 2,692 .
−6
s
52 ⋅ 10 s
Damit ist
u = Δt ⋅ S t →s
Für den Streuwinkel θ gilt:
θ≈
u
f
,wobei f = 300 ± 6 mm
5
Min.
t / µs
± 0,5µs
1
2
3
4
2,15
6,65
9,4
11
σ u / mm
u / mm
0,197
0,609
0,860
1,007
0,046
0,049
0,052
0,055
Mittelwert
σ d / mm
d / mm
0,482
0,468
0,552
0,660
0,540
0,113
0,039
0,035
0,038
0,056
Abb.3: Aufgenommene Messwerte am Doppelspalt mit zeitlichen Abständen t , sowie
realen Abständen u und der daraus berechnete Spaltabstand d
Für
den
Abstand
d
der
Spalte
ergibt
sich
aus
Gleichung
(1)
und
(3)
d = (0,540 ± 0,056) mm . Der auf dem Doppelspalt abgedruckte Wert beträgt
d = 0,5 mm .
2.2 Beugung an einem zweidimensionalen Transmissionsgitter
Es sollen die Gitterperioden d x und d y für ein Transmissionsgitter bestimmt werden.
Dazu wird der gleiche Aufbau wie in 2.1 verwendet (siehe Abb. 2). Anstelle des
Doppelspaltes wird ein Transmissionsgitter in den Strahlengang eingeführt. Mit der
CCD-Kamera werden analog zu 2.1 die Beugungsminima 1. Ordnung in x- und yRichtung mit einander per Oszilloskop vermessen und d gemäß Gleichung (1)
berechnet.
t / µs
± 0,5µs
x-Richtung
y-Richtung
9,9
9,9
u / mm
0,906
0,906
σ u / mm
0,053
0,053
d / mm
0,105
0,105
σ d / mm
0,006
0,006
Abb.4: Aufgenommene Messwerte am Transmissionsgitter mit zeitlichen Abständen t ,
sowie realen Abständen u und der daraus berechneten Gitterperioden d x und d y
Bei dem uns vorliegenden Gitter sind die horizontale Abstände gleich den vertikalen
Abständen der Gitterelemente:
d x = d y = (0,105 ± 0,006) mm
6
2.3 Beugung an einem eindimensionalen Transmissionsgitter
Im Folgenden wird die Gitterkonstante eines eindimensionalen Strichgitter mit
wiederum
gleichen
Aufbau
(siehe
2.1)
bestimmt.
Aufgrund
der
großen
Beugungswinkel wird anstatt der CCD-Kamera ein einfacher Schirm verwendet um
die Abstände u der Maxima des Beugungsbildes zur optischen Achse zu vermessen.
Es ergibt sich mit Hilfe von Gleichung (2):
Maximum
u / mm
σ d / mm
d / µm
± 1 mm
1
2
3
187,5
377,5
575,5
Mittelwert
1,194
1,617
2,141
1,650
0,005
0,002
0,001
0,002
Abb.5: Gemessene Abstände u der Beugungsmaxima eines Strichgitters mit der
berechneten Gitterkonstante d
Der aus der Messung hervorgehende Spaltabstand beträgt d = (1,650 ± 0,002 ) µm .
Dieser Wert weicht um 5,8% von der Firmenangabe ( d f =
1
mm = 1,754 µm ) ab.
570
2.4 Beugung an zweidimensionalen Reflexionsgitter
2.4.1 Beugung am CCD-Target
In dieser Messung soll die periodische Anordnung der Pixel auf dem CCD-Target
bestimmt werden. Dazu positionieren wir einen Schirm zwischen Linse und CCDKamera, um die Reflexion des Laserstrahles sichtbar zu machen und die Abstände u
der Maxima von der optischen Achse zu vermessen. Der Abstand f zwischen CCDKamera und Schirm beträgt f = (14,6 ± 0,1) cm . Es ergibt sich mit Hilfe von Gleichung
(2):
Maximum
1
2
3
u x / mm
u y / mm
± 1 mm
± 1 mm
21
43
--
14
28
42
Mittelwert
d x / µm
σ d / µm
x
9,062
8,920
--
0,429
0,203
--
8,991
0,316
d y / µm
6,787
6,809
6,846
6,814
σ d / µm
y
0,968
0,482
0,320
0,590
Abb.6: Gemessene Abstände ux und uy der Beugungsmaxima des CCD-Targets mit den
berechneten Pixelabständen dx und d y
7
Die Mittelwerte von d x = (8,991 ± 0,316) µm und d x = (6,814 ± 0,590) µm entsprechen
inklusive Standardabweichung ungefähr den theoretischen Erwartungen von
d x = 9,3 µm und d x = 6,3 µm . Die Abweichung beträgt 3,4% bzw. 7,6% .
2.4.2 Beugung an einer CD
Auf gleicher Weise wie in 2.4.1 wird nun der Spurabstand auf einer CD vermessen.
Der Abstand zwischen CD und Schirm ist f = 6,0 cm . Es ergibt sich:
Maximum
1
2
u / mm
± 1 mm
29
111
Mittelwert
d / µm
σ d / µm
1,454
1,439
1,446
0,451
0,061
0,256
Abb.7: Gemessene Abstände u der Beugungsmaxima einer CD mit den berechneten
Spurabstand d
Im Vergleich zum tatsächlichen Wert von d = (1,6 ± 0,1) µm sind wir innerhalb des
Toleranzbereichs und haben eine Abweichung von 9,7% .
2.4.3 Beugung an einer DVD
Auf gleicher Weise wie in 2.4.2wird nun der Spurabstand auf einer DVD vermessen.
Der Abstand zwischen DVD und Schirm betrug f = 5,8 cm . Es ergibt sich:
Maximum
u / mm
d / µm
σ d / µm
± 1 mm
1
102
0,728
0,035
Abb.8: Gemessene Abstände u der Beugungsmaxima einer DVD mit den berechneten
Spurabstand d
Im Vergleich zum tatsächlichen Wert von d = (0,74 ± 0,01) µm sind wir innerhalb des
Toleranzbereichs und haben eine Abweichung von 1,7% .
8
2.5 Beugung an Zufallstrukturen
In diesem Versuch beobachten wir das Beugungsbild einer Einfach- und
Doppellochzufalls-Struktur.
Das Beugungsbild einer Doppellochstruktur sah dem
Beugungsbild der Einfachlochstruktur sehr ähnlich. Es waren erwartungsgemäß cos²förmige Beugungsringe zu erkennen.
Abb.9: Kosinusförmiges Interferenzmuster
Zusätzlich
konnte
man
bei
der
Doppellochstruktur
schwache,
Beugungsmaxima und –minima erkennen, deren Position
senkrechte
jedoch nur schwer
auszumachen war. Diese Streifen wurden im 0. Maximum mittels Folie auf dem TVMonitor skizziert. Die realen Abstände der Beugungsminima wurden durch Messung
der skizzierten Abstände der Minima auf dem Monitor berechnet. Dabei entsprach
der Breite des Monitors ( 28 cm ) einem Abstand von ( 4,76 ± 0,02) mm auf dem CCDTarget. Wir erhielten folgenden Messwert und den daraus berechneten Abstand d
der Doppellöcher:
d = (2,606 ± 0,137) mm
9
3. Beantwortung der Fragen
Frage 1: Die resultierende elektrische Feldstärke ist gegeben durch die Superposition
beider Wellen:
E (α , t ) = E 0
sin α
⋅ e i (ωt − kr ) (e iΔφ + e −iΔφ )
α
, wobei α :=
kD
sin θ
2
Für den Verlauf der Intensität des Beugungsbildes eines Doppelspaltes bilden wir den
zeitlichen Mittwelwert der Feldstärke E ² :
⎛ sin α ⎞ iΔφ
− iΔφ
I (α ) = I 0 ⎜
⎟ e +e
⎝ α ⎠
2
(
)
2
2
⎛ sin α ⎞
= I0 ⎜
⎟ (cos Δφ + i ⋅ sin Δφ + cos Δφ − i ⋅ sin Δφ )
⎝ α ⎠
2
2
⎛ sin α ⎞
⎛ sin α ⎞
= I0 ⎜
⎟ (2 ⋅ cos Δφ ) = 4 I 0 ⎜
⎟ cos ² Δφ
⎝ α ⎠
⎝ α ⎠
2
2
Dabei entspricht I 0 der Maximalintensität.
Frage 2: Analog zu Frage 1
2
2
iNΔφ
iNΔφ
−1
− 1 e iNΔφ − 1 ⎞⎟
⎛ sin α ⎞ e
⎛ sin α ⎞⎛⎜ e
= I0 ⎜
⋅
I (α ) = I 0 ⎜
⎟ iΔφ
⎟
− iΔφ
− 1 e −iΔφ − 1 ⎟⎠
⎝ α ⎠ e −1
⎝ α ⎠⎜⎝ e
iNΔφ / 2
− e −iNΔφ / 2
⎛ sin α ⎞⎛⎜ e
= I0 ⎜
⎟
− iΔφ / 2
− e −iΔφ / 2
⎝ α ⎠⎜⎝ e
2
2
2
⎞
⎟ = I ⎛⎜ sin α ⎞⎟⎛⎜ sin( NΔφ / 2) ⎞⎟
0
⎜
⎟
⎟
⎝ α ⎠⎝ sin(Δφ / 2) ⎠
⎠
Frage 3:
d
Abb.10:Beugung am Reflexionsgitter
Die Ergebnisse aus den drei Versuchen sind zufrieden stellend. Bei der Ausbreitung
einer ebenen Lichtwelle verlaufen die Wellenfront geradlinig. Erst nach der Reflexion
am jeweiligen Objekt entsteht ein Phasenunterschied, der zu einem Interferenzmuster
führt.
10
In der Praxis sind die Wellenfronten gekrümmt und nicht geradlinig. Das´bedeutet,
dass die Lichtstrahlen vor der Reflexion am Objekt untereinander phasenverschoben
sind. Außerdem kann ebenfalls durch das Strahlaufweitungssystem eine Abweichung
hervorgerufen werden. Bei der Strahlaufweitung wird nämlich die Phasenlage der
einzelnen Lichtstrahlen verändert.
11
Literaturverzeichnis
Breuer, Hans, dtv-Atlas Physik, 6. Auflage, Deutscher Taschenbuch
Verlag GmbH & Co. KG München, September 2005
Helmers, Dr. Heinz, Skript zum Anfängerpraktikum Physik II, CvO
Universität Oldenburg, Institut für Physik, April 2006
Halliday, David, Physik, Wiley VCH GmbH, Weinheim, 2003
12