Übersicht Teil 1 - Atomphysik - IUP
Werbung

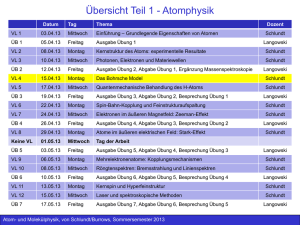
Übersicht Teil 1 - Atomphysik Datum Tag Thema Dozent Schlundt VL 1 03.04.13 Mittwoch Einführung – Grundlegende Eigenschaften von Atomen ÜB 1 05.04.13 Freitag Ausgabe Übung 1 VL 2 08.04.13 Montag Kernstruktur des Atoms: experimentelle Resultate Schlundt VL 3 10.04.13 Mittwoch Photonen, Elektronen und Materiewellen Schlundt ÜB 2 12.04.13 Freitag Ausgabe Übung 2, Abgabe Übung 1, Ergänzung Massenspektroskopie VL 4 15.04.13 Montag Das Bohrsche Model Schlundt VL 5 17.04.13 Mittwoch Quantenmechanische Behandlung des H-Atoms Schlundt ÜB 3 19.04.13 Freitag Ausgabe Übung 3, Abgabe Übung 2, Besprechung Übung 1 VL 6 22.04.13 Montag Spin-Bahn-Kopplung und Feinstrukturaufspaltung Schlundt VL 7 24.04.13 Mittwoch Elektronen im äußeren Magnetfeld: Zeeman-Effekt Schlundt ÜB 4 26.04.13 Freitag Ausgabe Übung 4, Abgabe Übung 3, Besprechung Übung 2 VL 8 29.04.13 Montag Atome im äußeren elektrischen Feld: Stark-Effekt Keine VL 01.05.13 Mittwoch Tag der Arbeit ÜB 5 03.05.13 Freitag Ausgabe Übung 5, Abgabe Übung 4, Besprechung Übung 3 VL 9 06.05.13 Montag Mehrelektronenatome: Kopplungsmechanismen Schlundt VL 10 08.05.13 Mittwoch Röngtenspektren: Bremsstrahlung und Linienspektren Schlundt ÜB 6 10.05.13 Freitag Ausgabe Übung 6, Abgabe Übung 5, Besprechung Übung 4 VL 11 13.05.13 Montag Kernspin und Hyperfeinstruktur Schlundt VL 12 15.05.13 Mittwoch Laser und spektroskopische Methoden Schlundt ÜB 7 17.05.13 Freitag Ausgabe Übung 7, Abgabe Übung 6, Besprechung Übung 5 Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 Langowski Langowski Langowski Langowski Schlundt Langowski Langowski Langowski 1 Zusammenfassung der letzten Vorlesung Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 2 Experimenteller Befund Spektroskopie an Alkalimetallen (z.B. Natrium) zeigt, dass viele der optischen Übergänge nicht einfache Linien sind, sondern Dubletts, oder Tripletts Aber: s-Zustände (l=0) sind nicht aufgespalten Die berühmte Natrium D-Linien (589,96/589,59 nm) entsprechen dem Übergang: 3P 3S Grund: Energietermaufspaltung durch Wechselwirkung von magnetischem BahnMoment und magnetischem Spin-Moment Na-D Linien D Sonnenspektrum handkoloriert von Josef v. Fraunhofer Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 3 Magnetisches Moment der Bahnbewegung I Ein Kreisstrom der Stärke I, der die Fläche A umschließt erzeugt ein magnetisches Dipolmoment Einheit: [] = Am2 Steht senkrecht auf der Fläche A In einem magnetischen Feld B erfährt das magnetische Dipolmoment ein Drehmoment: Das magnetische Dipolmoment besitzt im magnetischen Feld eine potentielle Energie, die von der relativen Orientierung von magnetischem Moment und Magnetfeld abhängt: Denn: Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 4 Magnetisches Moment der Bahnbewegung II Wie sieht nun das magnetische Dipolmoment der Elektronenbahn aus? Berechne das magnetische Moment eines Elektrons auf einer Kreisbahn: Das magnetische Moment des Kreisstroms is dann: Betrachte den Bahndrehimpuls: Denn: Damit besteht zwischen dem magnetischen Moment und dem Bahndrehimpuls die Beziehung: „Magnetomechanischer Parallelismus“: (Anti-) Parallelität zwischen magnetischem Moment und Bahndrehimpuls Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 5 Magnetisches Moment der Bahnbewegung III Die Einheit des magnetischen Moments ist das Bohrsche Magneton Dabei handelt es sich um das magnetische Moment, das dem Bahndrehimpuls der ersten Bahn des Bohrschen Modells (mit l=ħ) entspricht. Man schreibt auch: mit dem g-Faktor oder Landé-Faktor gl = 1 g-Faktoren sind stets definiert als das Verhältnis von magnetischem Moment in Bohrschen Magnetonen und dem Drehimpuls in der Einheit ħ: Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 6 Richtungsquantelung des Bahndrehimpulses im Magnetfeld Die Orientierung des Bahndrehimpulses in einem äußeren Magnetfeld nicht beliebig. Die z-Komponente kann nur bestimmte Werte annehmen. “Richtungsquantelung” Der Betrag des Drehimpulses ist gegeben durch: mit l = 0,1,…,n-1 Die z-Komponente kann folgende Werte annehmen: ml = -l, -l+1,…0,…,l-1,l ml : magnetische Quantenzahl Es galt: Für die z-Komponente entsprechend: Oder: Experimenteller Nachweis der Richtungsquantelung durch Stern-Gerlach Experiment Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 7 Spin und magnetisches Moment des Elektrons I Einführung des Elektronenspins im Jahre 1925 durch Uhlenbeck und Goudsmit, um spektroskopische Messungen zu erklären: Atome im s-Zustand (Bahndrehimpuls l = 0) haben kein magnetisches Bahnmoment alle Ein-Elektron-Atome im Grundzustand sollten diamagnetisch sein, tatsächlich sind sie aber paramagnetisch Ursache ist der Eigendrehimpuls oder Spin der Elektronen und das damit zusammenhängende magnetische Moment Analog zum Bahndrehimpuls gilt für den Betrag des Spins: mit der Spin-Quantenzahl s = 1/2 Für das magnetische Moment des Spins gilt: Experimentell ermittelt: gs = 2,0023 Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 8 Spin und magnetisches Moment des Elektrons II In einem äußeren Magnetfeld kann der Spin nur 2 mögliche Orientierungen einnehmen (Richtungsquantelung des Spins): “parallel” und “antiparallel” Für die z-Komponente des Spins (B-Feldlinien parallel zu z-Achse) gilt: ms = -1/2,+1/2 (magnetische Spin-QZ) Damit gilt für die z-Komponente des magnetischen Spin-Moments: Oder: Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 9 Spin und magnetisches Moment des Elektrons III Gyromagnetisches Verhältnis : ist definiert als das Verhältnis von magnetischem Moment und Drehimpuls bei Bahn-Magnetismus Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 bei Spin-Magnetismus 10 Messung des gyromagnetischen Verhältnisses I Die Änderung der Magnetisierung Nadel ist die Summe der Änderungen für alle Elektronen: N: Gesamtzahl der Elektronen Das bedeutet für die makroskopische Änderung des Drehimpulses der Nadel LNadel : Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 11 Messung des gyromagnetischen Verhältnisses II Gemessen wurde: Damit gilt: Oder: g = 2 Diese Methode ermöglicht die Feststellung, ob SpinMagetismus oder Bahn-Magnetismus dominiert Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 12 Das Stern-Gerlach-Experiment (1921) Potentielle Energie der magnetischen Momente im Magnetfeld: für: Die Kraft in z-Richtung: Winkel zwischen magnetischem Moment und Richtung des Feldgradienten Klassisch sind alle Werte für erlaubt. Im Experiment werden sowohl für H als auch Ag 2 mögliche Ablenkungen beobachtet. Elektronenkonfiguration von Ag: 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p6 4d10 5s1 Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 13 Das Stern-Gerlach-Experiment (1921) Schlussfolgerungen aus dem Stern-Gerlach-Experiment: • Experimenteller Nachweis der Richtungsquantelung • Quantitative Auswertung ergibt: z = ± B (S = - mS gS B, mS = ±1/2, gS 2) • Für alle Atome, die als äußeres Elektron ein s-Elektron haben, erhält man denselben Wert die magnetischen Momente der inneren Elektronen heben sich gegenseitig auf Man misst also auch bei Ag den Spinmagnetismus • Das s-Elektron hat den Bahndrehimpuls l = 0. Es wird also nur der Spinmagnetismus gemessen Experimenteller Hinweis auf die Existenz des Elektronenspins Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 14 Feinstruktur und Spin-Bahn-Kopplung I Feinstruktur (FS): Aufspaltung der Energieterme bei Atomen mit einem Valenzelektron (mit Ausnahme der s-Zustände) in 2 Unterzustände, die zu einer Dublett-Struktur der Spektrallinien führt. Qualitative Erklärung: Die FS wird verursacht durch die Wechselwirklung zwischen dem magnetischen Bahn-Moment und dem magnetischen Spin-Moment des Elektrons, der sog. “Spin-Bahn-Kopplung”. Die Kopplung der magnetischen Momente geht einher mit der Kopplung von Bahndrehimpuls und Eigendrehimpuls zu einem Gesamtdrehimpuls Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 15 Feinstruktur und Spin-Bahn-Kopplung II Für den Gesamtdrehimpuls gilt: j ist die Gesamtdrehimpuls-Quantenzahl Es gilt: j = | l ± s |, d.h., j = | l ± ½ | für ein Einelektronensystem (s = ½) Richtungsquantelung des Gesamtdrehimpulses: Die z-Komponente jz kann bestimmte Werte annehmen: wiederum nur mj = -j, -j+1,…0,…,j-1,,j Damit hat der Gesamtdrehimpuls 2j + 1 Einstellungsmöglichkeiten Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 16 Feinstruktur und Spin-Bahn-Kopplung III Beispiele: 1) Für ein Elektron im p-Zustand: l = 1, s = ½ j = 1/2 oder j = 3/2 2 Möglichkeiten: Der j = 3/2 Zustand ist 4-fach entartet, da die magnetische Gesamtdrehimpulsquantenzahl folgende Werte annehmen kann: mj = -3/2, -1/2, 1/2, 3/2 2) Für einen s-Zustand ist l = 0 und damit j = s. Es gibt keine Termaufspaltung!! Auswahlregel: für optische Übergänge gilt : j = 0, 1 Allerdings sind Übergänge von j = 0 zu j = 0 verboten Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 17 Spin-Bahn Aufspaltung im Bohrschen Atommodell I • Durch Umlauf des Elektrons um den Kern wird ein Magnetfeld erzeugt, in dem sich das magnetische Moment des Elektrons orientiert und abhängig von der Orientierung eine bestimmte potentielle Energie besitzt. • Aus Sicht des Elektrons rotiert der Kern um das Elektron Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 18 Spin-Bahn Aufspaltung im Bohrschen Atommodell V Zusammenfassung: • Durch Wechselwirkung des Elektrons mit dem Bahnmoment wird jedes Niveau (mit Ausnahme von l = 0) in 2 Niveaus aufgespalten P a/2 P3/2 (j =3/2, l=1, s=1/2) -a P1/2 (j =1/2, l=1, s=1/2) • s-Zustände sind nicht aufgespalten (l = 0, j = s) • Feinstrukturaufspaltung ist proportional zu Z4 • Feinstrukturaufspaltung am größten bei kleinen Hauptquantenzahlen Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 22 Niveauschemata der Alkali-Atome Auswahlregeln: l = 1 (d.h., der Bahndrehimpuls muss sich ändern), und j = 0, 1 S n=4 3/2 1/2 n=3 n=2 P 1/2 3/2 1/2 1/2 D F 5/2 7/2 5/2 3/2 1. Hauptserie: 2S1/2 – 2P1/2 und 2S1/2 – 2P3/2 Dubletts Scharfe Hauptserie: 2P1/2 – 2S1/2 und 2P3/2 – 2S1/2 5/2 3/2 Dubletts Diffuse Nebenserie: 2P1/2 – 2D3/2, 2P3/2 – 2D3/2 und 2P3/2 – 2D5/2 Tripletts 3/2 1/2 1/2 Erlaubte Übergänge 2P 3/2 2P 1/2 Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 2D 5/2 2D 3/2 Verbotener Übergang, da j = 2 wäre 23 Zusammenfassung Atom- und Molekülphysik, von Schlundt/Burrows, Sommersemester 2013 24