Studentisches Skriptum zu diesem Teil
Werbung

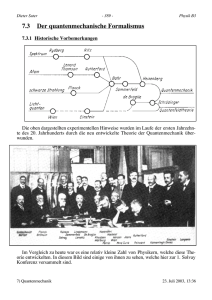
2. Projektarbeit Quantenmechanik SS 2008 (P. Penker, J. Perner, T. Rollett, R. C. Schardmüller, D. Wolbang) 3.1 Die Schrödingergleichung Die Bilder zeigen quantenmechanische Wellenfunktionen, im Speziellen die grafische Auflösung der Schrödinger-Gleichung. (Quelle: uni-graz) Inhalt Einführung .................................................................................................................................. 3 Erwin Schrödinger.................................................................................................................. 3 Allgemeines ............................................................................................................................ 3 Die freie Schrödingergleichung.............................................................................................. 4 Mathematische Formalismen ..................................................................................................... 5 Das Eigensystem des Hamiltonoperators ................................................................................... 7 Schrödingerbild vs. Heisenbergbild ......................................................................................... 10 Schrödingerbild .................................................................................................................... 10 Der Zeitentwicklungsoperator .............................................................................................. 10 Differentialgleichung für den Zeitentwicklungsoperator ..................................................... 11 Heisenbergbild ..................................................................................................................... 12 Herleitung der Heisenberggleichung .................................................................................... 12 Kommutatorrelationen ......................................................................................................... 14 Quellen ..................................................................................................................................... 15 2 Quantenmechanik - Die Schrödingergleichung Einführung: Erwin Schrödinger Erwin Schrödinger wurde am 12.8.1887 in Wien geboren. Von 1906 bis 1910 studierte er Mathematik und Physik an der Universität Wien, wobei er besonders durch die Arbeiten des theoretischen Physikers Fritz Hasenöhrl beeinflusst wurde. Nach seiner Habilitation 1914 in Wien nahm er am ersten Weltkrieg als Offizier der Festungsartillerie teil. Nachdem er an den Universitäten in Wien, Jena, Stuttgart und Breslau tätig gewesen war, übernahm er 1921 den Lehrstuhl für Physik der Universität Zürich, 1927 als Nachfolger von Max Planck den Lehrstuhl für theoretische Physik der Universität Berlin. 1928 wurde er korrespondierendes Mitglied im Ausland der Österreichischen Akademie der Wissenschaften (ÖAW). 1933 erhielt Erwin Schrödinger gemeinsam mit dem Engländer Paul Dirac für die Entwicklung der Wellenmechanik den Nobelpreis für Physik. Nach der Machtergreifung der Nationalsozialisten in Deutschland ging er 1934 nach Oxford. 1936 übernahm er eine Professur in Graz, musste 1938 emigrieren und lehrte am „Institute for Advanced Sciences“ in Dublin. 1956 kehrte er nach Wien an das Institut für theoretische Physik der Universität zurück und starb 5 Jahre später am 4.1.1961 in Wien. Allgemeines Die Schrödingergleichung ist eine bzw. die zentrale Grundgleichung der nichtrelativistischen Quantenmechanik. Die Lösungen dieser Gleichung werden auch Wellenfunktionen genannt. Diese Wellenfunktionen beschreiben die räumliche und zeitliche Entwicklung des Zustands eines Quantensystems. Die Gleichung wurde 1926 von Erwin Schrödinger (1887–1961) zuerst als Wellengleichung aufgestellt, mit der ihm die Erklärung der Spektren des Wasserstoffatoms gelang. Als „Bewegungsgleichung der Quantenmechanik“ bildet sie noch heute das Fundament für fast alle praktischen Anwendungen der Quantenmechanik und schon ab den 1920er Jahren gelang mit ihr die Erklärung vieler Eigenschaften von Atomen und Molekülen 3 Quantenmechanik - Die Schrödingergleichung (wo die Elektronenwellenfunktion als Orbitale bezeichnet werden) sowie von Festkörpern (Bändermodell). Die Schrödingergleichung ist die einfachst mögliche Differentialgleichung, die experimentellen Resultaten genügt und gewisse Symmetriebedingungen erfüllt. Die freie Schrödingergleichung Zunächst versuchen wir die freie Schrödingergleichung aufzustellen - die Feldgleichung für die Wellenfunktion Ψ ( r,t ) eines freien Teilchens: Eine deduktive Ableitung ist ebenso möglich wie etwa für die Maxwellgleichungen. Maxwell- und Schrödingergleichungen sind als einfachste mögliche Beschreibungen empirischer Sachverhalte anzusehen. Sie sind zugleich sehr erfolgreiche Gleichungen, indem sie ein ganzes Gebiet von Tatsachen beschreiben und Vorhersagen ermöglichen. Sowohl Photonen als auch Elektronen unterliegen dem Welle-Teilchen-Dualismus. Für Photonen, deren Ruhemasse null ist, gelten die Maxwellgleichungen. Die Analogie zwischen Photonen und Elektronen legt nahe, von den Maxwellgleichungen auszugehen und sie in geeigneter Weise auf Teilchen mit endlicher Ruhemasse zu verallgemeinern. Dies führt zu einer relativistischen Wellengleichung für die Wellenfunktion eines massiven Teilchens. Der nichtrelativistische Grenzfall der so gewonnenen Gleichung ist die sogenannte freie (oder kräftefreie) Schrödingergleichung. Man erhält sie direkt aus der Energie-Impuls-Beziehung E = p² / 2m und den Ersatzregeln E → iℏ∂ ² / ∂t und p → −iℏ∇ : iℏ∂ / ∂tΨ ( r,t ) = − ℏ ² / 2m∇ ²Ψ ( r,t ) Freie Schrödingergleichung Anwendungen (allgemeine Schrödingergleichung): - Spektrum des Wasserstoffatoms - Atomkerne, Bindungsenergien - Spektren und Strahlungsarten - Schwere-Quark Systeme 4 Quantenmechanik - Die Schrödingergleichung Mathematische Formalismen Wir betrachten nun die Zeitentwicklung eines Operators. Dabei ist zu beachten dass es für die Zeit keinen Operator gibt, sondern die Zeit als Parameter betrachtet wird. Angenommen wir α gegeben ist. Für einen allgemeinen Zustand haben einen Zustand zur Zeit t0 der durch wollen wir demnach finden α = α ,t = t0 => α ,t . Wir wollen nur die Zeitentwicklung des Zustandes studieren. Wie im Fall einer Translation, die zwei Kets sind durch einen Operator miteinander verknüpft, wir nennen diesen Operator dem Zeitentwicklungsoperator U (t , t0 ) . Smit gilt U (t , t0 ) α , t = t0 Zum Zeitpunkt t0 erhalten wir α ,t0 = ∑c t a 0 = αt . α a Ansonsten erhalten wir α , t = t0 = ∑ ca (t ) α a Daraus folgt ∑ c (t ) α a = 0 ∑ c (t ) α a a a Aus der Forderung dass die Wahrscheinlichkeit erhalten sein muss α ,t0 2 = α ,t 2 Folgt dass es sich um eine unitäre Operation handelt: α , t0 α , t0 = α , t0 1 α , t0 = α , t0 U †U α , t0 = α , t α , t Es gilt wegen Unitarität U = U † −1 und deswegen U U = 1 . † Um diesen Operator zu linearisieren definiert man eine Reihe des Operators mit einem hermitischen Operator H (Hamiltonoperator). i U (t + dt , t ) = 1 − Hdt + O( dt ) 2 ℏ Nun gilt weiterhin: i i † i i † i2 UU = 1 − Hdt 1 + H dt = 1 − Hdt + H dt − 2 HH † dt 2 = ℏ ℏ ℏ ℏ ℏ † i 1 − (H − H † ) = 1 ℏ 5 Quantenmechanik - Die Schrödingergleichung Aus dieser Bedingung sieht man dass H − H = 0 sein muss, um die Unitarität des † Zeitentwicklungsoperators zu erfüllen. H = H † gilt. D.h. der Hamiltonoperator muss hermitisch sein. Der Zeitentwicklungsoperator U selbst ist dimensionslos, deshalb ergibt sich für den Hamiltonoperator: i U (t + dt , t ) = 1 − Hdt ℏ => [ H ] = [ℏ] Js = = J = [E] [dt ] s [dt ] ≅ s [ℏ] = Js Der Operator H hat also die Dimension einer Energie. Für die Wirkung des Hamiltonoperators ergibt sich schließlich durch Vergleich und Differentialbildung die Schrödingergleichung für den Zeitentwicklungsoperator. i U (t + dt , t )U (t , t0 ) = 1 − Hdt U (t , t0 ) + O(dt ) 2 ℏ i U (t + dt , t )U (t , t0 ) = U (t , t0 ) − Hdt ⋅ U (t , t0 ) + O(dt )2 ℏ Es gilt U (t + dt , t )U (t , t0 ) = U (t + dt , t0 ) weil U (t1 , t2 )U (t2 , t3 ) = U (t1 , t3 ) i U (t + dt , t ) − U (t , t0 ) = − Hdt ⋅ U (t , t0 ) + O(dt ) 2 ℏ Daraus folgt nun U (t + dt , t0 ) − U (t , t0 ) i = − H ⋅ U (t , t0 ) dt ℏ => iℏ ∂ ∂ U (t , t0 ) = H ⋅ U (t , t0 ) => H = iℏ ∂t ∂t Oder Ausführlicher: => iℏ ∂ i ∂ U (t , t0 ) = − H (t , t0 ) => ℏ U (t , t0 ) = −iH ⋅ U (t , t0 ) ∂t ℏ ∂t ∂ U (t , t0 ) = −i 2 H ⋅ U (t , t0 ) ∂t => =-1 6 Quantenmechanik - Die Schrödingergleichung iℏ ∂ U (t , t 0 ) = H ⋅ U (t , t 0 ) ∂t Hieraus folgt nun die Schrödingergleichung für einen allgemeinen Zustand iℏ ∂ U (t , t0 ) α , t0 = H ⋅ U (t , t0 ) α , t0 ∂t Weiters gilt U (t , t0 ) α , t0 = => iℏ α ,t : ∂ α ,t = H α ,t ∂t α ,t Man muss schließlich drei verschiedene Fälle unterscheiden je nachdem, ob es eine Zeitabhängigkeit des Hamiltonoperators gibt oder nicht. U (t − t0 ) = e a) H ist zeitunabhängig b) H ist zeitabhängig aber es gilt [ H (t ), H (t ′)] = 0 U (t − t 0 ) = e i − H ( t −t0 ) ℏ t − i dt ′H ( t ′ ) ℏ t0 ∫ c) H ist zeitabhängig Lösung über Dysen-Reihe Wenn man nun die Darstellung des Hamiltonoperators sucht und weiß, dass es ein Energieoperator sein wird, kann man versuchen aus der klassischen Physik ein Analogon zu finden um dies in den Quantenmechanischen Fall zu übertragen (als Operator). Falls es ein solches Analogon nicht gibt (z.B. Spin) muss man einen Operator erst finden. Im Fall des Hamiltonoperators folgt für den klassischen Fall: Klassische Physik: E = T +V = p2 + V ( x) 2m Das Eigensystem des Hamiltonoperators Hier werden nur Eigensysteme diskutiert, in denen die Eigenkets von H auch die Eigenkets von A sind: [ H , A] = 0 d.h. H und A sind kompatible Operatoren. Im Eigensystem von A gilt: H a = Ea a 7 Quantenmechanik - Die Schrödingergleichung Für den Zeitentwicklungsoperator gilt dann: i i i U (t , t0 ) = exp − Ht = ∑ a a exp − Ht a ' a ' = ∑ a a exp − Eat a ' a ' = ℏ a ,a ' ℏ ℏ a ,a ' i ∑ exp − ℏ E t a a a ,a' i i a a ' a ' = ∑ exp − Eat a δ aa ' a ' = ∑ exp − Eat a a ℏ ℏ a a ,a' Man sieht, dass für eine Basis kompatibler Operatoren die Zeitentwicklung eines Zustandes durch die Zeitentwicklung des Eigenkets vollständig beschrieben ist. α , t0 = ∑ a α , t0 a = ∑ ca (t0 ) a a i a i α , t = ∑ exp − Eat α , t0 = ∑ exp − Eat ca (t0 ) α = ∑ ca (t ) α ℏ ℏ a a a Hieraus geht unmittelbar hervor, dass die Kenntnis eines allgemeinen Zustandes zum Zeitpunkt t = 0 sofort zur Kenntnis eines allgemeinen Zustandes zum Zeitpunkt t führt. Die Exponentialfunktion bedeutet lediglich einen Phasenfaktor und deshalb ca (t ) = ca (t0 ) . Dadurch ist die QM im Bezug auf Zustände eine streng deterministische Theorie. Erst durch die Wahrscheinlichkeitsinterpretation geht dieser Aspekt wieder verloren. Es gibt eine maximale Menge von Operatoren, die mit H kommutieren, durch deren Kenntnis man eine vollständige Beschreibung des Systems vornehmen kann. Für einen Eigenzustand von H gilt: B a .t i i = a, t B a, t = a, t0 U t BU a, t0 = a, t0 exp Eat B exp − Eat a, t0 ℏ ℏ = a , t0 B a , t0 8 Quantenmechanik - Die Schrödingergleichung Da die Zeitabhängigkeit für den Erwartungswert keine Rolle spielt, spricht man hier von stationären Zuständen. Für einen allgemeinen Eigenzustand von H gilt: B ∑ a ,a t a .t i i a ' , t0 ca' exp Ea dt B exp − Ea dt ca a, t0 ℏ ℏ i ' c E exp ( ' − Ea )t a , t0 B a , t0 a a ℏ a ∑c a ,a t = a, t B a, t = a, t0 U t BU a, t0 = ' Da es sich hierbei um eine Überlagerung von Zuständen handelt und diese somit nicht mehr stationär sind, spricht man von einem zeitabhängigen Erwartungswert. An dieser Stelle sei erwähnt, dass Interferenzterme für Wellenpakete zu einer Ungleichung der Form ∆t ⋅ ∆E ≥ iℏ führen. Da es aber keinen Zeitoperator gibt, folgt diese Relation nicht wie etwa die Orts-Impuls-Unschärfe einer Kommutatorbeziehung! Die Genauigkeit der Energie-Messung hängt somit von der Messzeitspanne ab. 9 Quantenmechanik - Die Schrödingergleichung Schrödingerbild vs. Heisenbergbild In der Quantenmechanik lässt sich nicht entscheiden, ob die Wahrscheinlichkeitsverteilung eines Messwertes sich zeitlich ändert, weil sich der Zustand zeitlich ändert oder weil sich der Messapparat zeitlich ändert. Hierin liegt die Unterscheidung zwischen dem Schrödinger- und dem Heisenbergbild. Schrödingerbild Das Schrödingerbild der Quantenmechanik, ist ein Modell für den Umgang mit zeitabhängigen Problemen. Im Schrödingerbild gelten folgende Annahmen: - Zustände sind nicht zeitabhängig: ψ = const - Operatoren sind zeitabhängig: Aˆ = Aˆ (t ) - Die Dynamik des Systems wird mit der Schrödingergleichung beschrieben iℏ ∂ ψ (r , t ) = Hˆψ (r , t ) ∂t Der Zeitentwicklungsoperator Im Schrödingerbild entwickelt sich der Zustand eines Systems also mit der Zeit. Die Entwicklung eines geschlossenen Quantensystems wird durch einen unitären Operator, den Zeitentwicklungsoperator U(t,t0), beschrieben. Der Operator wirkend auf ein Zustandsket zum Zeitpunkt t0 gibt das Zustandsket zu einem späteren Zeitpunkt t wieder ψ (t ) = U (t , t0 ) ψ (t0 ) Für Bras ψ (t ) = ψ (t0 ) U † (t , to ) 10 Quantenmechanik - Die Schrödingergleichung Der Zeitentwicklungsoperator besitzt 3 Eigenschaften: - Der Operator ist unitär: die Norm des Zustandskets darf sich mit der Zeit nicht ändern. ψ (t ) ψ (t ) = ψ (t0 ) U † (t , t0 )U (t , t0 ) ψ (t0 ) daher U (t , t0 )U (t , t0 ) = I † - Offenbar ist U(t0,t0) = I ψ (t0 ) = U (t0 , t0 ) ψ (t0 ) da - Die Zeitentwicklung von t0 zu t kann als Zeitentwicklung von t0 zu einer Zwischenzeit t1 und von t1 zur endgültigen Zeit t. daher U(t,t0) = U(t,t1)U(t1,t0) Differentialgleichung für den Zeitentwicklungsoperator Für t0 = 0 kann die Schrödingergleichung geschrieben werden als iℏ d U (t ) ψ e (0) = HU (t ) ψ e (0) dt Hier ist H der Hamiltonoperator für das System. Da ψ (0) ein konstanter Ket ist (es ist das Zustandsket bei t = 0) sehen wir, dass der Zeitentwicklungsoperator die Schrödingergleichung erfüllt. iℏ d U (t ) = HU (t ) dt Der Hamiltonoperator ist zeitunabhängig und die Lösung der obigen Gleichung lautet U (t ) = e − iHt ℏ Wo wir auch die Tatsache verwendet haben, dass bei t = 0 U(t) sich zum Identitätsoperator vereinfachen muss. Wir erhalten daher ψ (t ) = e − iHt ℏ ψ (0) . ψ (0) ist hier ein beliebiger Ket. Sollte jedoch das Ausgangsket ein Eigenzustand des Hamiltonoperators mit Eigenwert a sein erhalten wir ψ (t ) = e − iat ℏ ψ (0) . 11 Quantenmechanik - Die Schrödingergleichung Wir sehen daher, dass die Eigenzustände des Hamiltonoperators stationäre Zustände sind. Falls der Hamiltonoperator zeitabhängig ist, aber die Hamiltonoperatoren zu unterschiedlichen Zeitpunkten kommutieren, dann kann der Zeitentwicklungsoperator geschrieben werden als U (t ) = e − i t ℏ ∫ H (t′)dt′ 0 Heisenbergbild Die Alternative zum Schrödingerbild ist die Formulierung der Quantenmechanik mit zeitabhängigen Operatoren und zeitunabhängigen Zustandskets. In der Quantenmechanik des Heisenbergbilds ändert sich das Zustandsket ψ nicht mit der Zeit und ein Operator A erfüllt d ∂A A = (iℏ) −1[ A, H ] + dt ∂t classical In mancher Hinsicht ist das Heisenbergbild natürlicher und fundamentaler als das Schrödingerbild, besonders für relativistische Theorien. Insbesondere die Lorentzinvarianz ist ersichtlich im Heisenbergbild. Generell ist auch die Ähnlichkeit mit der klassischen Physik ersichtlicher. Durch Austausch des obigen Kommutators mit der Poissonklammer wird die Heisenberggleichung zu einer Gleichung aus der Hamiltonmechanik. Herleitung der Heisenberggleichung Sei A ein linearer hermitescher Operator. Der Erwartungswert von A für einen gegebenen Zustand ψ (t ) ist gegeben durch A t = ψ (t ) A ψ (t ) oder geschrieben entsprechend der Schrödingergleichung ψ (t ) = e − iHt ℏ ψ (0) 12 Quantenmechanik - Die Schrödingergleichung erhalten wir iHt A t = ψ (0) e ℏ Ae − iHt ℏ ψ (0) wir definieren iHt ℏ A(t ) := e Ae − iHt ℏ Nun iHt iHt iHt − d i i iHtℏ ∂A ℏ ℏ + e A ⋅ ( − H )e ℏ A(t ) = He Ae + dt ℏ ∂t classical ℏ differenzieren entsprechend der Produktregel iHt − i iHt i ∂A ∂A ( HA − AH )e ℏ + e = ( HA(t ) − A(t ) H ) + ℏ ℏ ∂t classical ℏ ∂t classical der letzte Ausdruck gilt, da e − iHt ℏ mit H kompatibel ist i ∂A = [ H , A(t )] + ℏ ∂t classical wir erhalten d i ∂A A(t ) = [ H , A(t )] + dt ℏ ∂t classcial Verwendung der Operatoridentität e B Ae − B = A + [ B, A] + 1 1 [ B,[ B, A]] + [ B,[ B,[ B, A]]] + ... 2! 3! wir sehen, dass man für einen zeitunabhängigen Operator A erhält it t2 it 3 A(t ) = A + [ H , A] − [ H ,[ H , A]] − [ H ,[ H ,[ H , A]]] + ... ℏ 2!ℏ2 3!ℏ3 Aufgrund der Relation zwischen der Poissonklammern und den Kommutatoren gilt diese Beziehung auch für die klassische Mechanik. 13 Quantenmechanik - Die Schrödingergleichung Kommutatorrelationen Offenbar sind die Kommutatorrelationen aufgrund der Zeitabhängigkeit der Operatoren von denen des Schrödingerbildes verschieden. Wir betrachten die Operatoren X(t1), X(t2), P(t1) und P(t2). Die Zeitentwicklung dieser Operatoren hängt vom Hamiltonoperator des Systems ab. Für den eindimensionalen harmonischen Oszillator p 2 mω 2 x 2 H= + 2m 2 Die Entwicklung der Orts- und Impulsoperatoren ist gegeben durch d i p x(t ) = [ H , x(t )] = dt ℏ m d i p (t ) = [ H , p (t )] = − mω 2 x dt ℏ Durch Differenzieren der beiden Gleichung und Lösung mit Randbedingungen p (0) = − mω 2 x(0) p (0) x (0) = m führt zu x(t ) = p0 cos(ωt ) + p0 sin(ωt ) ωm p (t ) = p0 cos(ωt ) − mω x0 sin(ωt ) Nun lassen sich die Kommutatorrelationen direkt berechnen [ x(t1 ), x(t2 )] = iℏ sin(ωt2 − ωt1 ) mω [ p (t1 ), p (t2 )] = iℏmω sin(ωt2 − ωt1 ) [ x (t1 ), p (t2 )] = iℏ cos(ωt2 − ωt1 ) NB: für t1 = t2 erhält man einfach die wohlbekannten kanonischen Kommutatorrelationen. 14 Quantenmechanik - Die Schrödingergleichung Quellen: Fließbach Torsten (2005), Quantenmechanik. Lehrbuch zur Theoretischen Physik 3. München. ISBN 3-8274-1589-6. Claude J. u.a. (2008). Schrödingergleichung. http://de.wikipedia.org/wiki/Schr%C3%B6dingergleichung (16.06.08) ÖAW. Geschichte des Erwin Schrödinger-Preises. http://stipendien.oeaw.ac.at/geschichte-des-erwin-schroedinger-preises (16.06.08) Norbert Swoboda. Quanten-Ästhetik. Formschön und elegant – Visualisierung von Atomen. http://www.kfunigraz.ac.at/communication/unizeit/archiv/2000/heft5/5-00-01.html (16.06.08) www.physicsforums.com (18.06.08) www.physikon.de (18.06.08) http://tpri6b.gsi.de/~vanhees/faq/qm (18.06.08) http://www.kfunigraz.ac.at/communication/unizeit/archiv/2000/heft5/5-00-01.html (18.06.08) http://stipendien.oeaw.ac.at/geschichte-des-erwin-schroedinger-preises (18.06.08) http://de.wikipedia.org/wiki/Schr%C3%B6dingergleichung (18.06.08) 15 Quantenmechanik - Die Schrödingergleichung