Vom Raum in die Ebene Geometrie für den Anschauungsraum
Werbung
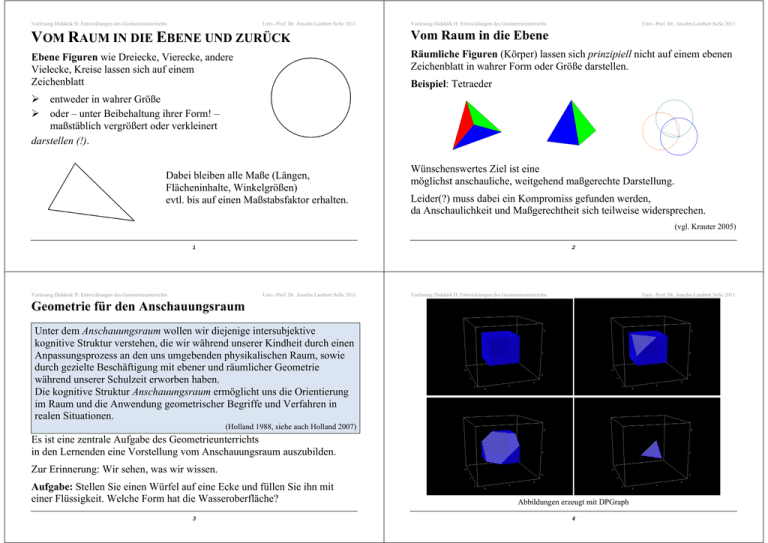
Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 VOM RAUM IN DIE EBENE UND ZURÜCK Vom Raum in die Ebene Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt Räumliche Figuren (Körper) lassen sich prinzipiell nicht auf einem ebenen Zeichenblatt in wahrer Form oder Größe darstellen. Beispiel: Tetraeder ¾ entweder in wahrer Größe ¾ oder – unter Beibehaltung ihrer Form! – maßstäblich vergrößert oder verkleinert darstellen (!). Dabei bleiben alle Maße (Längen, Flächeninhalte, Winkelgrößen) evtl. bis auf einen Maßstabsfaktor erhalten. Wünschenswertes Ziel ist eine möglichst anschauliche, weitgehend maßgerechte Darstellung. Leider(?) muss dabei ein Kompromiss gefunden werden, da Anschaulichkeit und Maßgerechtheit sich teilweise widersprechen. (vgl. Krauter 2005) 1 2 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Geometrie für den Anschauungsraum Unter dem Anschauungsraum wollen wir diejenige intersubjektive kognitive Struktur verstehen, die wir während unserer Kindheit durch einen Anpassungsprozess an den uns umgebenden physikalischen Raum, sowie durch gezielte Beschäftigung mit ebener und räumlicher Geometrie während unserer Schulzeit erworben haben. Die kognitive Struktur Anschauungsraum ermöglicht uns die Orientierung im Raum und die Anwendung geometrischer Begriffe und Verfahren in realen Situationen. (Holland 1988, siehe auch Holland 2007) Es ist eine zentrale Aufgabe des Geometrieunterrichts in den Lernenden eine Vorstellung vom Anschauungsraum auszubilden. Zur Erinnerung: Wir sehen, was wir wissen. Aufgabe: Stellen Sie einen Würfel auf eine Ecke und füllen Sie ihn mit einer Flüssigkeit. Welche Form hat die Wasseroberfläche? 3 Abbildungen erzeugt mit DPGraph 4 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Zur Erinnerung: Schülerinnen und Schüler stellen Körper dar (z. B. als Schrägbild) Einerseits: Zentralperspektive Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Wenn aus Kreisen Ellipsen werden – Teil 1 …. Perspektive Abbildung eines Kreises (z.B. Foto) Vorgabe: Die Darstellung soll möglichst anschaulich sein. Dabei wird ein Körper im Raum durch Projektionsstrahlen, die alle durch ein gemeinsames Zentrum verlaufen, auf eine Ebene projiziert. ¾ ¾ ¾ ¾ anschaulich wenig maßgerecht geradentreu, aber nicht parallelentreu nicht teilverhältnistreu (z.B. die Mitte bleibt nicht immer die Mitte) (vgl. Krauter 2005, und Scheid 2007, Abbildung erzeugt mit Euklid Dynageo) 5 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts 6 Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Schülerinnen und Schüler stellen Körper dar (z. B. als Schrägbild) Einerseits: Zentralperspektive Andererseits: Parallelprojektion ¾ konstruktiv aufwändig ¾ Entspricht der fotografischen Aufnahme Vorgabe: Die Darstellung soll weitgehend maßgerecht sein. Dabei wird ein Körper im Raum durch zueinander parallele Projektionsstrahlen, auf eine Ebene projiziert. ¾ weniger (?) anschaulich ¾ weitgehend maßgerecht ¾ geradentreu (falls Gerade nicht parallel zu Projektionsrichtung) und parallelentreu ¾ teilverhältnistreu (z.B. die Mitte bleibt immer die Mitte) ¾ konstruktiv einfach Realisierung durch Schattenwurf von Kantenmodellen (Knete und Schaschlikspießchen) im Sonnenlicht oder im Abblendlicht eines PKW. Anwendung in technischen Zeichnungen und Bauplänen. (vgl. Krauter 2005 und Scheid 2007) (vgl. Krauter 2005 und Scheid 2007) Abbildung links erzeugt mit Euklid Dynageo, Abbildung rechts: http://www.eiba.tuwien.ac.at/Lehre99/exkursionen/Russland/Schienen.jpg 7 8 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Spezialfälle der Parallelprojektion von besonderer Bedeutung: Wenn aus Kreisen Ellipsen werden – Teil 2 …. Kavalierprojektion (Bildebene vertikal: Wand) Parallelprojektion eines Zylinders ¾ Seitenansicht des Objekts in wahrer Größe ¾ Winkel zur dritten Achse frei wählbar üblich sind 135° (bzw. 45°) ¾ Verkürzungsfaktor frei wählbar üblich sind 21 oder 21 2 Bewegliche Konstruktion unter Ausnutzung der Eigenschaft „parallelentreu“. Welche Rolle spielen die Strahlensätze? Kästchendiagonale nutzen! Mit Winkel und Verkürzungsfaktor experimentieren! (vgl. Krauter 2005 und Scheid 2007) Welche Körper werden hier dargestellt? Abbildungen rechts erzeugt mit dem beweglichen Programm KOERPERGEOMETRIE Was haben die beiden Darstellungen gemeinsam, was unterscheidet sie? (http://www.mathe-schumann.de) 9 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts 10 Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Wie lassen sich Pyramiden und Tetraeder unterscheiden? Spezialfälle der Parallelprojektion von besonderer Bedeutung: Parallelprojektion eines Tetraeders Militärprojektion (Bildebene horizontal: Fußboden) ¾ Grundriss des Objekts in wahrer Größe ¾ Winkel zur dritten Achse frei wählbar üblich sind 120° (bzw. 60°) ¾ Verkürzungsfaktor frei wählbar üblich sind 21 bzw. 23 . (vgl. Krauter 2005 und Scheid 2007) Wie unterscheiden sich diese Darstellungen von den vorhergehenden? Abbildungen rechts erzeugt mit KOERPERGEOMETRIE Konstruktion? 11 12 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Unmögliche Figuren Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Aspekte des Geometrieunterrichts (vgl. Leitidee Raum und Form) ¾ ¾ ¾ ¾ ¾ ¾ Abbildungen: http://www.schneider-andre.net/optische-taeuschungen-unmoegliche-figuren.php Symmetrie Kongruenz Parallelen Koordinaten Konstruktionsaufgabe Darstellungen von Körpern (insbesondere: Grenzen der Darstellungsmöglichkeiten) ¾ Gedankliche Operation mit Körpern ¾ Analyse geometrischer Objekte des Raumes (vgl. auch Ernst 1998 und Scheid 2007) 13 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts 14 Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Noch mehr Möglichkeiten von Unmöglichem Abbildungen: http://www.schneiderandre.net/optische-taeuschungenunmoegliche-figuren.php 15 16 Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Noch mehr Möglichkeiten von Unmöglichem Vorlesung Didaktik II: Entwicklungen des Geometrieunterrichts Univ.-Prof. Dr. Anselm Lambert SoSe 2011 Und nicht zu vergessen: M.C. ESCHER Abbildungen: http://www.schneiderandre.net/optische-taeuschungenunmoegliche-figuren.php 17 Quelle: www.artchive. com bzw. www.mcescher .com 18