Fortsetzung: Arithmetik in Bildern (PDF

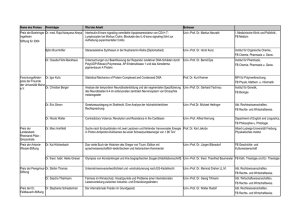
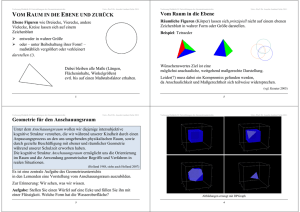
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Lösungen aus der Schule
Strategie: Vorwärts- und Rückwärtsarbeiten
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Weitere klassische
figurierte Zahlen
Hier „sieht“ man eher nichts ...
(STIFEL 1553, 44)
> Dreieckzahl(k)^2 + Dreieckzahl(k+1)^2;
Dreieckzahl(Dreieckzahl(k) + Dreieckzahl(k+1));
2
2
k 1 · § ( k2 ) 2 k
§ ( k1 )
·
¨¨
¸¸ ¨¨
1 ¸¸
2
2
2
2¹ ©
2
©
¹
2
2
„Ist das immer so?“
2
1 ( k2 ) 2 ·
§ ( k1 )
¨¨
¸¸
k 2
2
2
2
2
©
¹ ( k1 ) k 1 ( k2 )
2
4
4
2 4
33
34
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
... aber hier sieht man’s, wenn man zweimal hinschaut
Und wie sieht die Dreieckwurzel (von Stifel) aus?
(Abb. rechts nach: Nelsen 2000, 99)
Weil’s so „lustlich und lieblich“ ist:
L a n g s a m : Die Summe der
„Quadrate“(!) zweier
aufeinanderfolgender
Dreieckzahlen ist eine
Dreieckzahl, deren
Dreieckwurzel die Summe
der beiden Dreieckzahlen ist.
(STIFEL 1553, 46)
Diesen Zusammenhang beschrieben schon
Plutarch von Chäronea und Diophant.
Kuckucksklone
(Becker 1957, 42)
Wir sehen in diesem Münzenbild auch:
4 '(k ) 1
35
k 2 (k 1)2 und ...
36
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Weitere Beispiele (Entnommen aus den Sammlungen von Roger B. Nelsen)
Das magstu probiren
Noch einmal Summe der n ersten ungeraden Zahlen
n
4¦ (2k 1)
(STIFEL 1553, 46)
n
Meint kurz:
¦k
3
2
'(k ) . Ein klarer Gedanke – klar aufgeschrieben?
k 1
k 1
Und wir sehen ein neues Muster: „Siegerpodest“ ...
... vielleicht können wir’s ja brauchen?!
37
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
38
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Etwa dafür
Oder auch dafür
Noch einmal Summe
der n ersten Kuben
Summe von Quadraten
Noch einmal als
Verallgemeinerung der n
ersten ungeraden Zahlen !
4¦ k 3
k 1
(n 2 n )2
(n(n 1))2
In Kombination mit
Woraus folgt:
n
¦k 3
k 1
§ n(n 1) ·
¨
¸
2
©
¹
2
'(n )2
39
((2n 1) 1)2
40
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Dreieck –, Quadrat – ..... ...... ....... ........ Vieleckzahlen
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Sehen Sie Sechseckzahl(summ)en? – Oder mehr?
Die Struktur der k-ten n-Eckzahl verstehen am Beispiel der 6-ten 6-Eckzahl
(Wieder)Erkennen Sie etwas in diesen Bildern?
(Wieder)Erkennen Sie etwas in diesen Zahlen?
Term?
41
42
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Elementarmathematik vom höheren Standpunkt Arithmetik (und Algebra) als Prozess und Produkt Univ.-Prof. Dr. Anselm Lambert
Bleiben wir im Raum – Tetraederzahlen ...
Und jetzt?
Tn
n
n
k 1
k 1
¦ '(k ) ¦ k(n (k 1))
und
Tn
n(n 1)(n 2)
6
Wie muss man den Quader sechsteln?
und
Tn
§n 2 ·
¸¸
¨¨
© 3 ¹
Pascalsches Dreieck?
und .................................................................. und wie sieht’s eigentlich aus mit Dodekaeder zahlen ... und .............................................und.................................
43
44