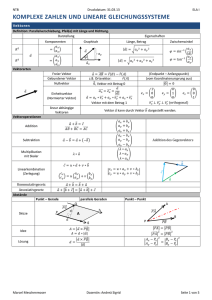
lineare abbildungen

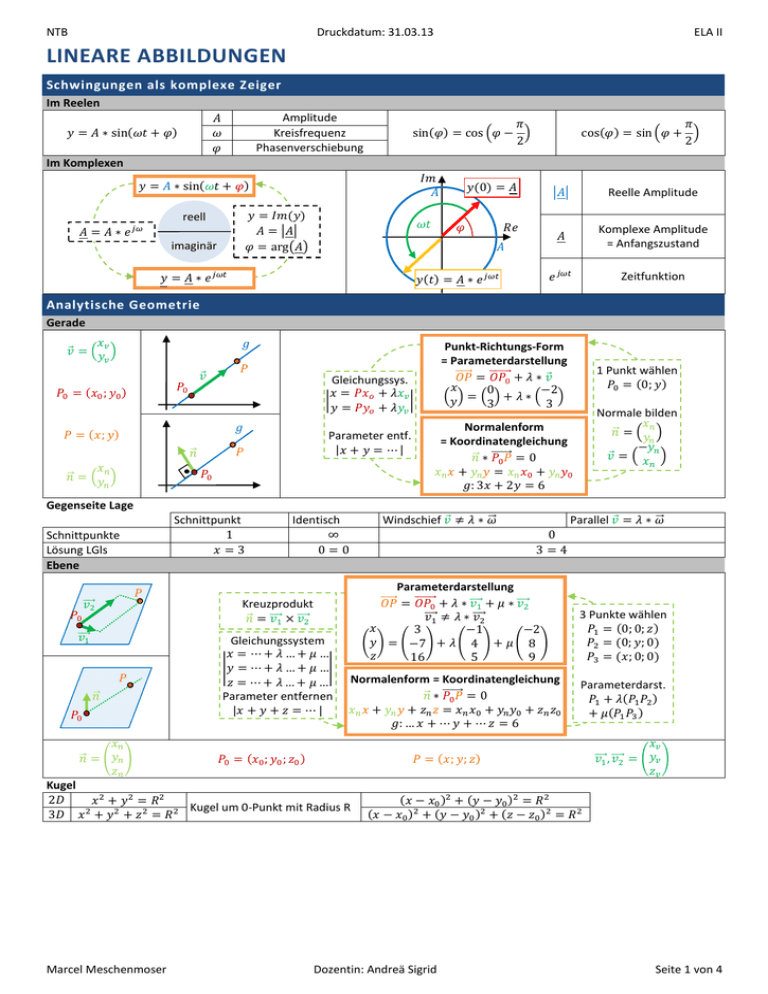
NTB
Druckdatum: 31.03.13
ELA II
LINEARE ABBILDUNGEN
Schwingungen als komplexe Zeiger
Im Reelen
Amplitude
Kreisfrequenz
Phasenverschiebung
Im Komplexen
Reelle Amplitude
reell
Komplexe Amplitude
= Anfangszustand
imaginär
Zeitfunktion
Analytische Geometrie
Gerade
Punkt-Richtungs-Form
= Parameterdarstellung
Gleichungssys.
1 Punkt wählen
Normale bilden
Parameter entf.
Normalenform
= Koordinatengleichung
Gegenseite Lage
Schnittpunkt
Identisch
Windschief
Parallel
Schnittpunkte
Lösung LGls
Ebene
Parameterdarstellung
Kreuzprodukt
3 Punkte wählen
Gleichungssystem
Normalenform = Koordinatengleichung
Parameter entfernen
Parameterdarst.
Kugel
Kugel um 0-Punkt mit Radius R
Marcel Meschenmoser
Dozentin: Andreä Sigrid
Seite 1 von 4
NTB
Spatprodukt / Determinante
Spatprodukt (3-teilige Determinante)
(für Volumenberechnung)
Druckdatum: 31.03.13
Determinante
2-reihig
ELA II
3-reihig
Handregel von Sarrus
Reihenfolge
zyklisches Vertauschen (drehen des Koordinatensystem)
Ansonsten Vorzeichen wechsel (spiegeln des Koordinatensystem)
Matrix / Matrizen
Definition
Matrix
(Grossbuchstabe)
Element einer Matrix
(Kleinbuchstabe)
A=[2 5 7;3 6 1]
A:=matrix([[2,5,7],[3,6,1]])
A(1,2)
->5
A(2,3)
->1
A[1,2]
->5
A[2,3]
->1
size(A)
-> 2 3
linalg::matdim(A) -> [2,3]
Dimension einer Matrix
Spezielle Matrizen
zeros(2,3)
matrix(2,3)
Nullmatrix
diag([4,6,8])
matrix(3,3,[4,6,8],Diagonal)
Diagonalmatrix
(quadratisch)
Symmetr. Matrix
(quadratisch)
eye(3)
matrix::identity(5)
Einheitsmatrix
(quadratisch)
ones(2,4)
2x4
Elementare Matrix-Operationen
Gleichheit
(gleiche Grösse & Inhalt)
Addition
(gleiche Grösse)
isequal(A,B) ->1/0
matrix::equal(A,B) ->true/false
A+B
A+B
2*A
2*A
Multiplikation mit Skalar
A´
linalg::transpose(A)
Transponierte
Marcel Meschenmoser
Dozentin: Andreä Sigrid
Seite 2 von 4
4
1
0
Modul 1
Modul 2
Modul 3
Modul 4
7
1
0
2
1
6
5
3
Syst. 1
Syst. 2
Syst. 3
Teil 2
2
0
2
ELA II
Teil 1
Modul 4
3
0
5
Teil 2
Modul 3
1
3
0
Teil 1
Modul 2
Syst. 1
Syst. 2
Syst. 3
Druckdatum: 31.03.13
Modul 1
NTB
Matrizenmultiplikation
Definition
18
23
5
41
6
40
A*B
A*B
Vorgehen Berechnung
1. Geht es aufgrund Grösse?
2. Grösse der resultierenden
Matrix
3. Ausrechnen
Eigenschaften
Kommutativgesetz
Distributivgesetz
Assoziativgesetz
Nullmatrix
Einheitsmatrix
Transponieren
Inverse Matrix (Matrizendivision gibt es nicht!)
Definition
Anwendung
 Quadratische Matrix

Orthogonale Matrix
Definition
Alle Zeilen-/Spaltenvektoren:
 Die Länge 1 haben
 Paarweise senkrecht(=orthogonal)
aufeinander stehen
(Skalarprodukt = 0)
Berechnung
Gauss-Jordan
(Gauss-Elimination)
Befehle
inv(A)
A^-1
Beispiel
Länge
orthogonal
Satz
Transponierte = Inverse
Rang und Determinante
Rang
Marcel Meschenmoser
Dozentin: Andreä Sigrid
Seite 3 von 4
NTB
Druckdatum: 31.03.13
ELA II
Lineare Abbildungen (= Funktion)
Definition
Muss durch den Ursprung gehen
Funktion mit Vektor
Abbildungsmatrix (nur Zahlen!!)
Komposition
Umkehrung
Spezielle lineare Abbildungen
Singuläre Abbildungen
Operation kann nicht rückgängig gemacht werden
Null-Abbildung
Setzt alles auf null
Projektion auf x
Projiziert auf die x-Achse
Projektion auf y
Projiziert auf die y-Achse
Reguläre Abbildungen
Operation kann rückgängig gemacht werden
Identität
Lässt alles gleich
Orthogonale Abbildung
Längentreu (und winkeltreu)
Rotationsabbildung
(Drehung)
Drehung um den Winkel
Streckung um
Streckung um den Faktor
Koordinatentransformation
1. Neues Koordinatensystem einführen
Erste Achse
Zweite Achse
die geg. Achse
Skalarprodukt
Rotation von Punkt P um die Achse um
Dritte Achse
Kreuzprodukt
2. Einheitsvektoren bilden
3. Abbildung, um auf neues Koordinatensystem zu übertragen
4. Transponierte
5. Rotationsmatrix (z.B.
Achse)
um die z- 6. Ausführen
Punkt P
ins blaue System
Rotation
ins rote System
Marcel Meschenmoser
Dozentin: Andreä Sigrid
Seite 4 von 4