k TB a

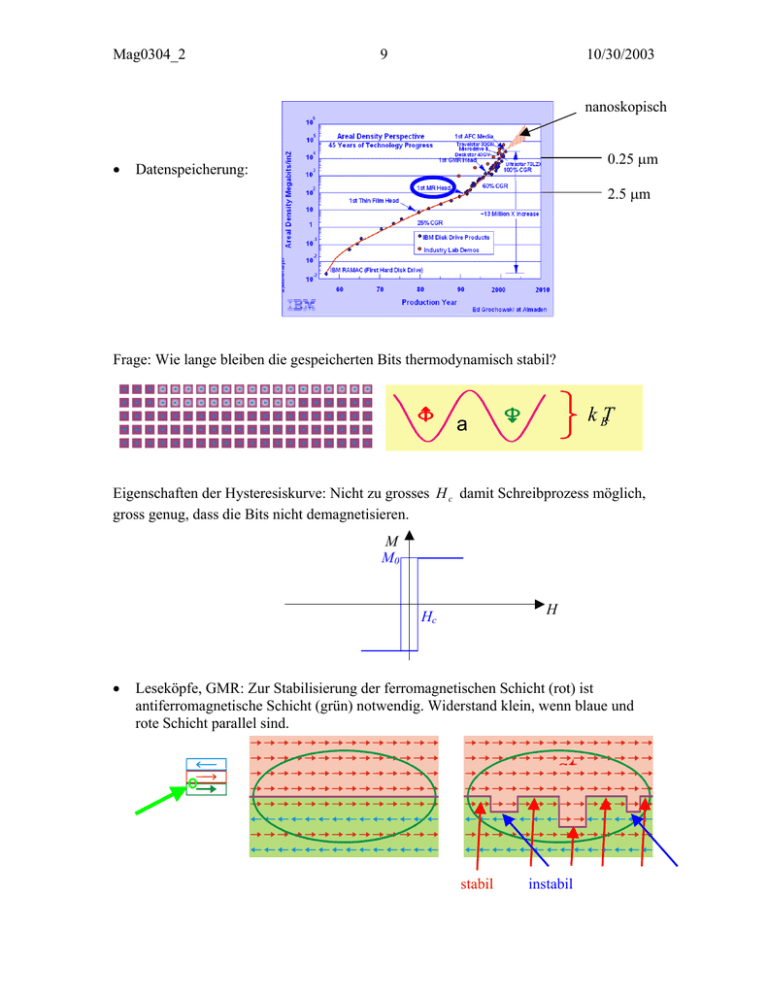
Mag0304_2
9
10/30/2003
nanoskopisch
•
0.25 µm
Datenspeicherung:
2.5 µm
Frage: Wie lange bleiben die gespeicherten Bits thermodynamisch stabil?
k BT
a
Eigenschaften der Hysteresiskurve: Nicht zu grosses H c damit Schreibprozess möglich,
gross genug, dass die Bits nicht demagnetisieren.
M
M0
H
Hc
•
Leseköpfe, GMR: Zur Stabilisierung der ferromagnetischen Schicht (rot) ist
antiferromagnetische Schicht (grün) notwendig. Widerstand klein, wenn blaue und
rote Schicht parallel sind.
st
stabil
instabil
Mag0304_2
10
10/30/2003
Zum Verständnis der Wirkungsweise von magnetischen Komponenten ist die Kenntnis
der atomaren Struktur notwendig.
Probenstab
Sekundärspule
Wie kann man magnetische Struktur messen?
Magnetometer:
ν = 1 MHz
λ = 300 m >> atomare Distanz
keine mikroskopische Information
Probe
Röntgen- oder Neutronenstrahlung:
Magnet
Primärspule
H(r,t)
r
λ ≈ 2 Å : entspricht atomaren Abständen Æ Interferenzerscheinungen
Röntgenstreuung:
2
•
•
 E 

Wechselwirkung ∝ 
2 
 me c 
Streuung proportional zur Anzahl ungepaarter Elektronen und nicht Z.
Beispiel Cu Kα ≈ 8 keV: Magnetische Streuung ist ca. 106 mal schwächer als Streuung
durch Ladungen Æ Synchrotronstrahlung verwenden. Ferromagnetische Strukturen nicht
messbar.
Neutronenstreuung:
Magnetische und nukleare
Wechselwirkung.
Beispiel:
Antiferromagnetismus in MnO (Shull
and Smart, Phys. Rev. 76, 1256 (1949).
Mag0304_2
11
10/30/2003
1.2. Warum ist mikroskopische Information über Magnetismus notwendig?
1.2.1. Magnetisierungsmessungen
Sättigungsmagnetisierung von Ferromagneten liefert magnetisches Moment n B pro Atom
in Einheiten des Bohr’schen Magnetons µ B : M 0 (T = 0) = Nn B µ B . N bezeichnet die
Anzahl Atome pro Volumeneinheit.
Substanz Magnetisierung
bei 0 K (Gauss)
EuS
EuO
Gd
Dy
Fe
Co
Ni
Ni3Al
1220
1920
2060
2920
1740
1446
510
Magnetisches
Curie
Magnetisierung
µ 0 M bei 0 K (T) Moment n B ( µ B ) Temperatur (K)
1.53
16.5
2.41
6.8
69.5
2.59
7.63
292
3.67
10.2
88
2.19
2.22
1043
1.82
1.72
1388
0.64
0.606
627
0.075
41
Die Substanzen in der Tabelle haben alle im wesentlichen L = 0 . Man erwartet also
ganz- oder halbzahlige Werte für n B . Man sieht sofort, dass die (itineranten)
Ferromagnete Fe, Ni, Co und insbesondere Ni3Al deutliche Abweichungen zeigen.
Erklärung: In seltenen Erden Systemen werden die ungepaarten Elektronen in der 4fSchale durch die äusseren Elektronen (5s2p6) abgeschirmt. Direkter Beweis:
Formfaktoren, magnetische Anregungen.
1.2.2. Suszeptibilität
Definition:
M = χH .
Für einen Paramagneten gilt das Curie-Weiss Gesetz:
χ = Ng 2 J ( J + 1) µ 0
µ B2
3k B T
.
J bezeichnet den Bahndrehimpuls und g das gyromagnetische Verhältnis. Aus dem
Curie-Gesetz erhält man das sogenannte effektive magnetische Moment (effective
number of Bohr magnetons)
µ eff = g J ( J + 1) µ B = p eff µ B .
Mag0304_2
12
10/30/2003
Der g-Faktor ist gegeben durch die Landé-Gleichung:
g = 1+
J ( J + 1) + S ( S + 1) − L( L + 1)
2 J ( J + 1)
In der folgenden Tabelle sind einige Werte für p eff bei Raumtemperatur angegeben:
Substanz
3+
Eu
Gd3+
Dy3+
Ni3Al
Config.
Level
6
4f
4f7
4f9
itinerant
7
F0
S7/2
6
H15/2
8
p eff = g J ( J + 1)
p eff = g S ( S + 1)
p eff = g J ( J + 1)
berechnet
berechnet
gemessen
0
7.94
10.63
Bei den seltenen Erden ist die Übereinstimmung der berechneten und gemessenen
Werten gut, mit Ausnahme von Eu3+ bei dem die Energiedifferenz zu höheren JMultiplets klein ist verglichen mit k B T Æ Kristallfeldmessungen mit Neutronen.
In Ni3Al erhält man µ eff = 1.2 µ B >> µ sat = 0.075µ B /Ni Atom (G. G. Lonzarich and L.
Taillefer, J. Phys. C: Solid State Phys. 18, 4339 (1985)).
Suszeptibilität von Dimeren:
Curie-Gesetz:
C
χ=
T
Messung des Anregungsspektrums mit Neutronen.
3.4
8.0
10.6
0.075
Mag0304_2
13
10/30/2003
1.2.3. Spezifische Wärme
 ∂U 
CV = 
 .
 ∂T V
Die spezifische Wärme ist gegeben durch
Die inelastischen Beiträge zur innere Energie U können folgendermassen berechnet
werden:
∑U
j
j
=∑
j
∞
∫ d Eρ
j
(E) g j (E) .
0
ρ j ( E ) ist die Energieeigenwertdichte und g j ( E ) gibt die Besetzungswahrscheinlichkeit
an (Fermi-Dirac Verteilung bzw. Bose-Einstein Verteilung). U j beschreibt inelastische
Anteile, wie zum Beispiel Phononen, Elektronen, Magnonen etc.
Die spezifische Wärme von Ce0.9La0.1Al3 (Schwerelektronensystem) ist ca. 300 mal
grösser als in Kalium. Da CV gegeben ist durch die Verteilung der Anregungen, kann man
durch Messung der inelastischen Streuung mit Neutronen herausfinden, welche Moden
für CV verantwortlich sind. In den folgenden zwei Figuren ist der Koeffizient γ = C / T
aufgetragen.
Das magnetische Anregungsspektrum liefert direkte Information über die spezifische
Wärme.
Mag0304_2
14
10/30/2003
Dramatische Unterschiede werden auch für lokalisierte und itinerante Ferromagnete
beobachtet. Offensichtlich sind die magnetischen Anregungen für EuO und Ni3Al sehr
verschieden.
D. T. Teaney et. al, Phys. Rev. Lett. 20, 722 (1968).
Specific Heat in EuO
Spezifische Wärme von Ni3Al:
TC
1.3. Magnetische Grundbegriffe
Dieser Abschnitt dient dazu, einige wichtige Grundbegriffe und Einheiten zu definieren.
1.3.1. Maxwell’sche Gleichungen
Die elektromagnetischen Eigenschaften werden durch die Maxwell’schen Gleichungen
beschrieben:
∂B
Gesetz von Faraday:
∇×E = −
∂t
Gesetz von Coulomb:
∇⋅D = ρ
∂D
Gesetz von Ampere:
∇×H = j+
∂t
Mag0304_2
15
10/30/2003
B ist quellenfrei:
∇⋅B = 0.
E: elektrische Feldstärke
(V/m)
D: dielektrische Polarisation (As/m2)
H: magnetische Feldstärke
(A/m)
B: magnetische Induktion
(Vs/m2)
j: elektrische Stromdichte
(A/m2).
ρ: elektrische Ladungsdichte (C)
Im Vakuum gilt:
B = µ0H
wobei
µ 0 = 4π ⋅ 10 −7 VsA -1m -1
ε 0 = 8.854 ⋅ 10 −12 AsV-1m -1
und
und
D = ε 0E ,
(Induktionskonstante)
(Dielektrizitätskonstante)
Im Medium führt man die neuen Grössen
P:
M:
elektrische Polarisation (As/m2) und
Magnetisierung (A/m) ein.
Sie sind mit den gemäss den Gleichungen
B = µ 0 (H + M )
und
B = µ 0 µH
D = ε 0 εE ,
und
D = ε 0 E + P oder
miteinander verknüpft. Die Materialkonstanten µ (magnetische Permeabilität) und ε
(Dielektrizitätskonstante) sind im allgemeinen Tensoren. Sie sind nur definiert, wenn
man über einen Bereich von sehr viele Atome mitteln kann (vgl. das Auftreten ε bei der
Diskussion von realen Halbleitern). Die Magnetisierung kann direkt mit der Beziehung
M = χH
berechnet werden ( µ = 1 + χ ). Die magnetische Suszeptibilität χ ist im allgemeinen
wieder ein Tensor 2. Stufe.
Wir werden sehen, dass χ die zentrale Grösse während der ganzen Vorlesung sein wird:
Sie beschreibt das magnetische Verhalten des Mediums.
1.3.2. Magnetische Momente = magnetische Dipole
Das fundamentale Objekt in magnetisierten Materialien ist das magnetische Moment.
zwischen magnetischen Momenten ist es praktisch, magnetische Momente (Einheit: Am2)
einzuführen. Für eine elementare Stromschleife gilt:
Mag0304_2
16
10/30/2003
dµ = IdS .
dµ
Auslöschung
der Ströme
dS
I
Für eine makroskopische Stromschleife erhält man durch Integration
µ = I ∫ dS .
In einem Atom kann eine Stromschleife entstehen, wenn sich ein Elektron mit der Masse
m um den Kern bewegt. Wie gross ist das magnetische Moment?
Der Drehimpuls ist quantisiert:
L = me vr = lh ⇒ vr =
Für den Kreisstrom erhält man
I =−
und für die Fläche
e
=−
τ
S=r π.
lh
.
me
ev
2πr
2
Das Moment beträgt also:
µ = IS =
evr
elh
− ev 2
r π =−
=−
= γL .
2πr
2
2me
Die Zahl γ = −e /(2me ) nennt man das gyromagnetische Verhältnis des Elektrons. µ
und L sind für das Elektron (wegen der negativen Ladung!) antiparallel zueinander.
Elektron:
Allgemein gilt:
L
µL
µ = γL .
Experiment dazu: Einstein-de Haas Effekt (1915).
Mag0304_2
17
Definition: Bohr’sches Magneton
µB =
eh
= 9.274 ⋅ 10 − 24 Am2.
2me
Definition: Nukleares Magneton
µN =
eh
= 5.051 ⋅ 10 − 27 Am2.
2m n
10/30/2003
µ N ist viel kleiner als das Bohr’sche Magneton und spielt normalerweise nur bei tiefsten
Temperaturen eine Rolle.
Ein magnetisches Material ist aus vielen magnetischen Momenten zusammengesetzt und
man definiert die Magnetisierung M (Am-1):
M = nµ .
Wobei n (m-3) die Anzahl der magnetischen Momente µ (Am2) pro Volumeneinheit
angibt.
Elektronen weisen neben dem orbitalen Moment noch ein intrinsisches Moment auf, den
Spin S, der die Werte s = ± 12 annehmen kann. Der Spin führt zu einem magnetischen
Moment, das gegeben ist durch
µ s = − gµ B s ,
wobei der g-Faktor gegeben ist durch g = 2.002 (?).
Ein magnetisches Moment erzeugt eine Feldstärke
H=
1  3(µ ⋅ r)r µ 
− 3

4π  r 5
r 
an der Position r. Auf einen Dipol µ wirkt in einem Magnetfeld B ein mechanisches
Drehmoment
G = µ×B.
dL
= G erhalten wir für die Bewegungsgleichung eines
dt
magnetischen Moments in einem Feld die Differentialgleichung
Ausgehend von der Gleichung
γ
dL
= γG
dt
⇔
dµ
= γµ × B .
dt