Physik des Sehens

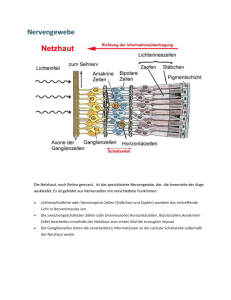
Physik des Sehens
Handout
Seminarvortrag Atom- und Festkörperphysik WS
2008/09
Philip Ketterer ([email protected])
Matthias Engelmann ([email protected])
2. März 2009
1
1
Das Auge
Abbildung 1: Schematische Darstellung des Auges
In Abbildung 1 ist ein Querschnitt des Auges dargestellt. Man erkennt den kugelförmigen Aufbau, der größtenteils durch den Glaskörper gefüllt ist. Die eigentliche Absorptions des Lichts findet
vollständig in der Netzhaut statt.
Einige wesentliche Eigenschaften des Auges sind:
• Optische Eigenschaften
Die Brechkraft des Auges ist die reziproke Brennweite D = f1 und wird in der Einheit
dpt = m−1 angegeben. Der größte Beitrag zur Brechkraft kommt durch die Grenzschicht
Luft-Hornhaut (ca. 49dpt). Die Gesamtbrechkraft beträgt 59dpt. Dies erklärt auch warum
man unter Wasser nur unscharf sehen kann.
• Akkomodation (Änderung der Brechkraft)
Durch den Ciliarmuskel ist das Auge in der Lage den vorderen Krümmungsradius der Linse zu
ändern, womit sich die Brechkraft ändert. Die Differenz der Brechkräfte bezeichnet man als
Akkommodationsbreite. Deren Wert ändert sich im Laufe eines Lebens von ca. 10dpt (Jugendjahre) auf ca. 1dpt (60 Jahre). Grund dafür ist das Wachstum und eine damit einhergehende
Verhärtung der Linse.
• Fehler der Augenoptik
Die Augenoptik unterliegt den für Linsen typischen optischen Abbildungsfehlern. Neben der
sphärischen und chromatischen Abberration kann man auch einen Astigmatismus feststellen.
Letzter ist besonders auffallend wenn man aus geraden Linien bzw. Schraffierungen bestehende
Objekte betrachtet.
2
Abbildung 2: Die Netzhaut
2
Die Netzhaut
In Abbildung 2 ist eine schematische Darstellung der Netzhaut gegeben. Auffallend ist, dass die
einfallenden Photonen zunächst die Nervenzellschicht durchdringen und erst danach auf die Rezeptorzellen treffen. Zwischen den Rezeptor- und den Nervenzellen sind sogenannte Interneurone, die
die Informationen weiterverarbeiten. Man unterscheidet zwei grundlegende Arten von Rezeptorzellen:
• Stäbchen
Stäbchen besitzen eine sehr geringe Reizschwelle, weshalb sie auch sehr geringe Lichtintensitäten wahrnehmen können. Das sogenannte Stäbchensehen findet als vorwiegend bei schwachen Lichtverhältnissen statt und es können keine Farben wahrgenommen werden. Zuständig
für die Photonenabsorption ist das sogenannte Rhodopsin (besteht aus Opsin und Retinal)
in der Zellmembran. Bei hohen Lichtintensitäten wird das Rhodopsin milchig und kann keine
Photonen mehr absorbieren.
• Zapfen
Bei den Zapfen unterscheidet man drei unterschiedliche Typen die jeweils ein anderes Absorptionsspektrum haben. Dies ermöglicht das Farbensehen. Das sogenannte Zapfensehen findet
meist bei ausreichend hoher Lichtintensität (z.B. tagsüber) statt. Die Reizschwelle der Zapfen
ist deutlich höher als die der Stäbchen.
Weiterhin gibt es zwei besondere Stellen der Netzhaut:
• Blinder Fleck
Den Punkt, an dem der innen liegende Sehnerv aus dem Auge heraustritt, bezeichnet man als
den sogenannten blinden Fleck. Dort sind keine Rezeptorzellen vorhanden. Durch Ergänzungseffekte von umliegenden Zellen wird dieser aber selbst bei einäugigem Sehen nicht wahrgenommen.
3
• Fovea centralis
Die Fovea centralis ist eine Vertiefung der Netzhaut im Zentrum mit einem Durchmesser von
ca. 3mm. Sie ist in Abb. 2 mit dargestellt. In diesem Bereich befinden sich ausschließlich
Zapfen in einer sehr dichten Anordnung, so dass lediglich Objekte, auf die dieser Punkt des
Auges gerichtet ist, scharf wahrgenommen werden können.
3
Neuronale Prozesse
Die reale menschliche Sehwahrnehmung lässt sich nicht durch eine reine physikalische Betrachtung des Auges verstehen. Eine Vielzahl von neuronalen Prozessen spielt eine Rolle. Beispielsweise
schafft es das Gehirn, Gegenstände in unterschiedlicher Entfernung, trotz deutlicher Größenunterschiede auf der Netzhaut, in die gleiche Größe zu umzurechnen. Dieses Phänomen bezeichnet
man als Größenkonstanz. Die genauen neuronalen Abläufe im Gehirn konnten bislang nur teilweise
entschlüsselt werden.
4
Farbensehen
Das Sehen von Farben steht mit keiner physikalischen Größe in einem einfach zu beschreibenden
Zusammenhang (ganz anders in der Akustik, dort sind Schallwellen direkt für das Hören von Tönen
verantwortlich). Deshalb muss man sich zum Verständnis des Farbensehens zunächst die physikalische Beschreibung des Farbreizes betrachten. Dies geschieht mit der sogenannten Farbreizfunktion
Φ(λ). Die Farbreizfunktion ist eine skalare Größe und hängt daher nicht direkt vom vektoriellen
Charakter des Lichts (also z.B. Polarisation), sondern zunächst nur von der Wellenlänge λ und
damit von der spektralen Zusammensetzung des ausgesandten Lichts ab:
Φ(λ) = γ(λ) · S(λ)
Dabei ist S(λ) die sogenannte Strahlungsfunktion, die im Wesentlichen eine spektrale Verteilungsfunktion ist, die durch einen willkürlichen Referenzwert geteilt wurde und daher dimensionslos
gesetzt, P0 ist eine
ist. Im Weiteren wird für S(λ) immer die spektrale Leistungsverteilung PP(λ)
0
konstante Leistung. Der Faktor γ liegt zwischen Null und Eins und ist eine materialspezifische
Bilanzgröße, die wesentlich von materialspezifischen Größen bestimmt sein wird (z.B. atomare Zusammensetzung, Absorptions- und Reflexionsfähigkeit, Oberflächenstruktur, ... ).
4.1
Remissionsgrad und additive Farbmischung
Um zu erklären warum bestimmte Flächen unter Beleuchtung eine charakteristische Farbe haben
(zur Vereinfachung geht man natürlich von einer ebenen Fläche aus, die diffus strahlt, d.h. unabhängig von der Einfallsrichtung des Lichts), führt man den sogenannten Remissionsgrad β(λ)
ein. Dieser ist definiert als das Verhältnis der Strahlungsdichte L nach der Reflexion bezogen auf
eine ideal abstrahlende Fläche (diffus und absorptionsfrei), deren technische Umsetzung Weißstandard genannt wird:
β(λ) =
4
L
LW S
Zur Erinnerung: unter der Stahlungsdichte einer Quelle versteht man deren Strahlungsleistung
pro Fläche, die in Richtung der Flächennormalen in eine Raumwinkeleinheit abgestrahlt wird.
Für die Farbreizfunktion Φ von Licht, das von einer Strahlungsquelle mit Strahlungsfunktion S
stammt und von einer Fläche mit Remissionsgrad β reflektiert wird, gilt also:
Φ = S(λ) · β(λ)
Die Wahrnehmung einer farbigen Oberfläche lässt sich also mittels eines Korrekturfaktors β(λ)
beschreiben. Dabei muss man beachten, dass die Farbreizfunktion nur für Wellenlängen von Null
verschieden sein wird, bei denen auch β 6= 0 gilt. Im Wesentlichen kann man sich den Remissionsgrad
β also als eine Art Gewichtungsfaktor vorstellen, der Bilanz darüber zieht welche Wellenlängen von
der Oberfläche durch innere Prozesse ”verschluckt” und welche wieder abgestrahlt werden. Da so
nicht mehr alle Wellenlängen zum Farbreiz beitragen, werden bei gleich bleibendem S verschiedene
Oberflächen im Allgemeinen verschieden farbig wahrgenommen.
Bei der additiven Farbmischung geht man nun davon aus, dass sich die Farbreize im Auge in
ihrer Wirkung addieren. Für den Fall, dass eine Lichtquelle auf eine Fläche strahlt, die nicht nur
einen, sondern mehrere Remissionsgrade besitzt gilt für die Farbreizfunktion:
Φ(λ) = S(λ) ·
N
X
βi
i=1
Bei dieser Formel wurde vorausgesetzt, dass die Bereiche mit unterschiedlichen βi eng benachtbart und nicht sonderlich ausgedehnt sind (also z.B. viele kleine Kreise), so dass das Auge diese
nicht mehr auflösen kann. Dies ist auch der prinzipielle Mechanismus in einem Farbfernseher.
4.2
Transmissionsgrad und subtraktive Farbmischung
Der Transmissionsgrad eines optischen Filters (ein Filter ist ein teilweise transparenter Körper, der
Teile des Spektrums absorbiert) der Dicke d ergibt sich aus dem bekannten Lambertschen Gesetz:
P (d) = P0 · e−αd
Wobei α der Absorptionskoeffizient ist.
Ähnlich wie beim Remissionsgrad definiert man den Transmissiongrad als das Verhältnis der
Leistung P0 des einfallenden Lichtes mit Wellenlänge λ vor und dessen Leistung P (d) nach dem
Durchlaufen des Filters:
τ (λ) =
P0
P (d)
Für N hintereinander liegende Filterschichten gilt daher:
τ (λ) = ΠN
i=1 τi (λ)
Genauere Untersuchungen zeigen, dass das Lambertsche Gesetz von der Konzentration c der
Absorptionszentren im Medium abhängt. Für kleine Konzentrationen gilt das sogenannte LambertBeersche Gesetz:
P = P0 e−σdc
5
Wobei die Größe σ hier wieder eine materialspezifische Konstante darstellt. Durch diese Gleichung werden natürlich auch die Transmissionkoeffizienten τ konzentrationsabhängig. Für die Farbreizfunktion ergibt sich aus den obigen Überlegungen:
Φ(λ) = τ (λ)S(λ)
In Analogie zum Remissiongrad β gilt für die Bedeutung des Transmissionsgrades τ für das
Farbensehen, dass nur die Wellenlängenbereiche zum Farbreiz im Auge beitragen, für die τ 6= 0
gilt. Man kann sich daher wieder vorstellen, dass der Transmissionsgrad als ein Gewichtungsfaktor
wirkt, der aufgrund von inneren Absorptionsprozessen gewisse Anteile im Spektrum verschluckt.
Dadurch ändert sich die spektrale Zusammensetzung des Lichts nach Durchlaufen des Filters und
damit auch die Farbwahrnehmung im Auge. Gemäß dem Lambert-Beerschen Gesetz hängt dieser
Gewichtfaktor nicht nur von der Anzahl und Ausdehnung der Schichten, sondern auch von der
darin vorherrschenden Konzentration der Absoprtionszentren (und damit wesentlich von materialspezifischen Größen) ab.
4.3
Unterschiede und Gemeinsamkeiten beider Farbmischungen
Beide Formen der Farbmischung basieren auf im Medium ablaufenden Absorptionsprozessen, die
mit Hilfe von den Bilanzgrößen β(λ) und τ (λ) beschrieben werden können, die beide wesentlich
von materialspezifischen Größen bestimmt sind. In beiden Fällen erhält man bei konstanter Strahlungsfunktion S ein gesamt β bzw. τ , das aus einzelnen βi bzw. τi zusammengesetzt ist und so die
Farbreizfunktion auf einen bestimmten spektralen Bereich einschränkt. Weiterhin können bei beiden Mischungsarten alle Farben durch drei Grundfarben gemischt werden, die sich bei Mischung im
gleichen Verhältnis zu weiß (additiv) bzw. schwarz (subtraktiv; schwarz bedeutet hier vollständige
Absorption im Filter) überlagern.
Bei der additiven Farbmischung geht man also von einer unbeleuchteten Oberfläche aus und
fügt immer mehr farbige Komponenten hinzu, während man bei der subtraktiven Farbmischung
aus dem einfallenden Licht mittels Filtern immer mehr Komponenten heraus nimmt. Legt man für
die additive Mischung die drei Grundfarben grün, blau, rot und für die subtraktive Farbmischung
magenta, cyan, gelb fest, sind diese im folgenden Sinn zueinander entgegengesetzt: Je zwei der
Grundfarben einer Mischungsart ergeben im gleichen Verhältnis gemischt eine Grundfarbe des
anderen Systems.
5
Literatur
• Wikipedia mit den Artikeln ”Netzhaut”, ”Auge”, ”Akkommodation”
• Christoph von Campenhausen - ”Einführung in die Psychophysik der Wahrnehmung”
• Bergmann, Schäfer - Band ”Optik”
• Demtröder - ”Experimentalphysik 2”
• Thews, Mutschler und Vaupel - ”Anatomie, Physiologie und Pathophysiologie des Menschen”
6