dv isotherme

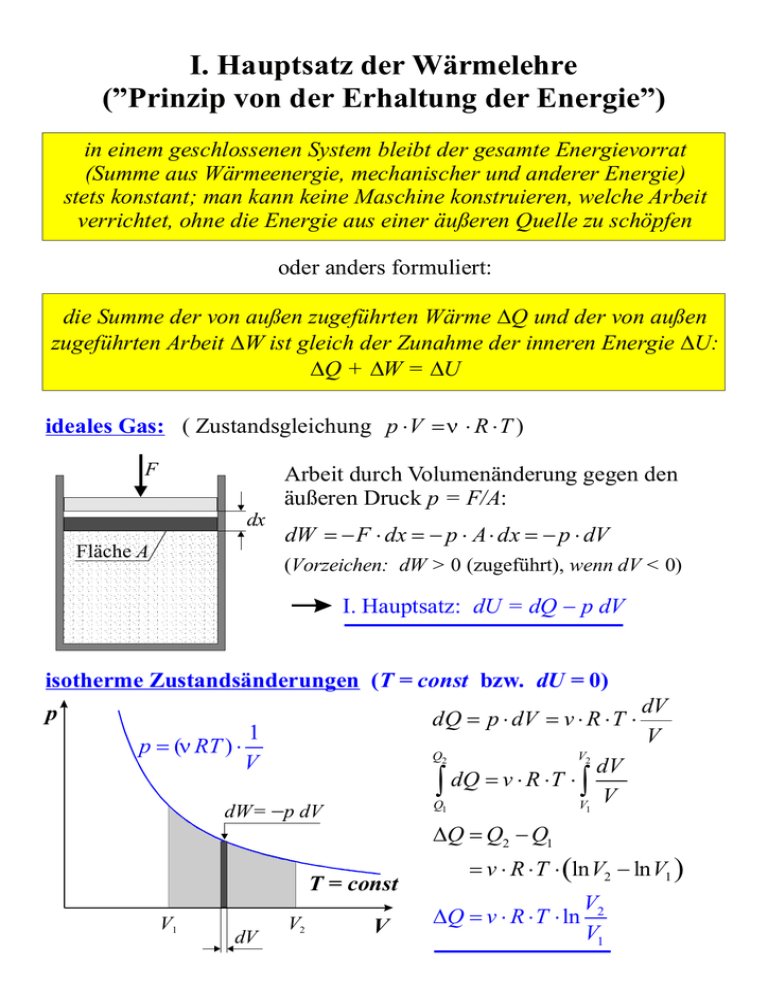
I. Hauptsatz der Wärmelehre
(”Prinzip von der Erhaltung der Energie”)
in einem geschlossenen System bleibt der gesamte Energievorrat
(Summe aus Wärmeenergie, mechanischer und anderer Energie)
stets konstant; man kann keine Maschine konstruieren, welche Arbeit
verrichtet, ohne die Energie aus einer äußeren Quelle zu schöpfen
oder anders formuliert:
die Summe der von außen zugeführten Wärme ∆Q und der von außen
zugeführten Arbeit ∆W ist gleich der Zunahme der inneren Energie ∆U:
∆Q + ∆W = ∆U
ideales Gas: ( Zustandsgleichung p ⋅ V = ν ⋅ R ⋅ T )
F
Arbeit durch Volumenänderung gegen den
äußeren Druck p = F/A:
dx
Fläche A
dW = − F ⋅ dx = − p ⋅ A ⋅ dx = − p ⋅ dV
(Vorzeichen: dW > 0 (zugeführt), wenn dV < 0)
I. Hauptsatz: dU = dQ − p dV
isotherme Zustandsänderungen (T = const bzw. dU = 0)
p
p = (ν RT ) ⋅
dQ = p ⋅ dV = v ⋅ R ⋅ T ⋅
1
V
Q2
V2
dV
V
V1
Q1
∆Q = Q2 − Q1
T = const
dV
V2
∫ dQ = v ⋅ R ⋅ T ⋅ ∫
dW= −p dV
V1
dV
V
V
= v ⋅ R ⋅ T ⋅ (ln V2 − ln V1 )
∆Q = v ⋅ R ⋅ T ⋅ ln
V2
V1
I. Hauptsatz der Wärmelehre
(adiabatische Zustandsänderung eines idealen Gases)
ideales Gas: ( Zustandsgleichung p ⋅ V = ν ⋅ R ⋅ T )
( innere Energie dU = ν ⋅ cmv ⋅ d T )
adiabatische Zustandsänderungen (dQ = 0)
(kein Wärmeaustausch des Systems mit der Umgebung)
I. Hauptsatz
dU = dW= − p dV
ν ⋅ cmv ⋅ d T = −ν ⋅ R ⋅ T ⋅
dV
V
⇒
dT
R dV
=−
⋅
T
cmv V
Integration: ln T = −
R
⋅ ln V + const
cmv
R cmp − cmv cmp
=
=
−1 = γ −1
cmv
cmv
cmv
⇒ ln T = − ln V γ −1 + const ⇒ ln T + ln V γ −1 = ln T ⋅ V γ −1  = const
T ⋅ V γ −1 = const
Anmerkung:
c
f +2
γ = mp =
cmv
f
pV = ν RT ⇒ T =
p
⋅V
νR
p ⋅V γ = const
Pneumatisches Feuerzeug
T ⋅ V γ −1 = T ⋅ V 2 / f = const
wegen γ − 1 =
f +2
2
−1 =
f
f
f Luft = ftrans + f rot = 3 + 2 = 5 (zweiatomige Moleküle)
Carnot'scher Kreisprozeß (I)
Expansion
Kompression
TH
TL
isotherm bei TH
Va
TH
adiabatisch
Vb
TH
Vb
TH
Vc
TL
isotherm bei TL
Vc
TL
Vd
TL
adiabatisch
Vd
TL
p
TH
TL
a
b
d
Va
Vd
c
Vb
Vc
V
Va
TH
Carnot'scher Kreisprozeß (II)
TH
TL
a
Wtot
b
Va
d
Vd
Prozess
a→b
(isotherm)
Vb
c
Vc
V
Volumen V
Arbeit
∆Wab = −v ⋅ R ⋅ TH ⋅ ln
Vb
Va
b→c
∆Wbc = − [U (TH ) − U (TL )]
(adiabatisch)
c→d
(isotherm)
∆Wcd = + v ⋅ R ⋅ TL ⋅ ln
Vc
Vd
d→a
∆Wda = − [U (TL ) − U (TH )]
(adiabatisch)
ausgetauschte
Wärme
Änderung der
inneren Energie
∆Qab = −∆Wab
∆U ab = 0
∆Qbc = 0
∆U bc = ∆Wbc
∆Qcd = −∆Wcd
∆U cd = 0
∆Qda = 0
∆U da = ∆Wda
Bilanz der Arbeit: Wtot = [| ∆Wab | + | ∆Wbc |]− [| ∆Wcd | + | ∆Wda |]

Vb
Vc 
= ν ⋅ R ⋅ TH ⋅ ln − TL ⋅ ln 
Va
Vd 

V
= ν ⋅ R ⋅ [TH − TL ]⋅ ln b
Va
b → c:
TH ⋅ Vbγ −1 = TL ⋅ Vcγ −1
d → a:
TH ⋅ Vaγ −1 = TL ⋅ Vdγ −1
Vb / Va = Vc / Vd
bzw.
ln(Vb / Va ) = ln(Vc / Vd )
Carnot'scher Kreisprozeß (III)
Wärme-Kraft-Maschine:
Umwandlung von Wärme-Energie in mechanische Arbeit
Definition des Wirkungsgrads η:
η=
Wtot von der Maschine verrichtete (= abgegebene) Arbeit
=
QH
aus dem heißen Reservoir aufgenommene Wärme
Wtot = ν ⋅ R ⋅ [TH − TL ]⋅ ln
Vb
Va
QH = ∆Wab = ν ⋅ R ⋅ TH ⋅ ln
⇒
Vb
Va
η=
TH − TL
T
=1− L <1
TH
TH
Richtungsumkehr des Kreisprozesses
Kälte-Maschine, Wärme-Pumpe:
Transport von Wärme vom tieferen auf ein höheres Temperaturniveau
TH
TL
a
Wtot
b
d
Va
Vd
Vb
c
Vc
Volumen V
Definition der Leistungszahl ε einer Wärmepumpe:
ε=
QH
Wtot
=
dem heißen Reservoir zugeführte Wärmemenge
durch die Maschine von außen zugeführte Arbeit
QH = ∆Wba = ν ⋅ R ⋅ TH ⋅ ln
Wtot = ν ⋅ R ⋅ [TH − TL ]⋅ ln
Vb
Va
Vb
Va
⇒
ε=
TH
>1
TH − TL