NMR Vortag im Rahmen des Fortgeschrittenen

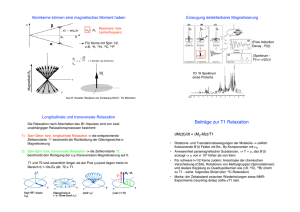
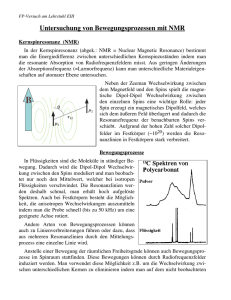
NMR
Vortag im Rahmen des Fortgeschrittenen-Praktikums
Martin Fuchs
1
Motivation
Die Nuclear Magnetic Resonance, oder zu
deutsch Kernspinresonanz ist vor allem durch
die aus der Medizin nicht mehr wegzudenkende Magnetresonanztomographie eine zumindest dem Namen nach weitläug bekannte physikalische Erscheinung. Die Physik
die dahintersteckt ist allerdings ebenso komplex wie spannend und soll in diesem Vortrag
näher beleuchtet werden.
2
Physikalische
Figure 1: Das Stern-Gerlach-Experiment
Grundla- wiederum aus den Spins der am Aufbau
beteiligten Quarks.(siehe Abbildung 2)
gen
2.1
Kernspin
Der Spin als intrinsische Teilcheneigenschaft
wurde erstmals 1925 postuliert um die Ergebnisse des Stern-Gerlach-Experiments zu erklären, bei dem ein Strahl aus Silberatomen im
Magnetfeld nicht wie klassisch erwartet kontiuierloich sondern diskret aufspaltet. Abbildung 1
Nach dem Standardmodell setzt sich der
Kernspin aus den Spins der Neutronen
und Protonen zusammen, und deren spin
Figure 2: Zusammensetzung des Kernspins
1
2.2
Verhalten des Kernspins im
B-Feld
Für uns ist das Verhalten des Kernspin in
äuÿeren Feldern, vor allem in einem äuÿeren
Magnetfeld von Interesse. Bei der Beschreibung dieses Verhaltens hilft uns die Tatsache, dass die Richtung des Spinvektors
der Richtung zugehörigen magnetischen Moments entspricht.
µ
~ Bahn
Figure 3: Der Spin als Projektion des Spinverktors
e ~
L
=
2mc
µ
~ Spin = g
e ~
S
2mc
Wir können uns nun deshalb als Modell des
Spinvektors einen Stabmagneten vorstellen,
der sich in einem Magnetfeld bendet. Dieser
wird versuchen sich entlang der Feldlinien
auszurichten. Da der Spin wie aus der Quantenmechanik bekannt nur die Projektion des
Spinvektors ist (siehe dazu Abbildung 3) und
der Spinvektor im Winkel zur z-Achse steht,
wird dieser der Kreiselgleichung gehorchend
eine Präzessionsbewegung ausführen, welche
sich beschreiben lässt durch ωL = γB0 . ωL
nennt man auch die Lamorfrequenz. Diese
ist, wie aus der Gleichung hervorgeht abhängig von der Stärke des Magnetfeldes und
vom gyromagnetischen Faktor γ der wie in
Tabelle 4 ersichtlich von Kern zu Kern verschieden ist.
Nun präzediert in einer makroskopischen
Probe nicht nur ein Spin sondern eine enorme
Anzahl an Spins mit der gleichen Frequenz
aber in allen möglichen Phasen sowie in
den beiden möglichen Ausrichtungen - entlang der Feldlinien bzw. entgegengesetzt
Figure 4:
dazu. Setzen wir alle diese Spinvektoren
gedanklich auf den Ursprung eines Koordinatensystems so können wir die resultierende
Magnetisierung, auch Nettomagnetisierung
genannt, als Vektorsumme der Einzelspins
betrachten. Veranschaulicht ist das in Abbildung 5.
2.3
Formale Beschreibung
Die eben angesprochenen Tatsachen helfen
uns, das Verhalten der Spins auf einer abstrakteren Ebene zu beschreiben. Wir transformieren die Spins und somit auch die
Netto-Magnetisierung in ein Koordinatensys2
Dieses Phänomen ist als Zeeman-Eekt
bekannt. Der Energieunterschied der der beiden Niveaus beträgt dE = h̄γB0 wobei wir
aber wissen, dass γB0 = ωL . Diese Zustände
können durch Emission bzw. Absorption
eines Photons mit der Energie Epho = h̄ωpho
ineinander übergehen, wobei ωpho = ωL sein
muss. Wir brauchen also für das Wechseln der Zustände resonantes Licht, was den
Begri Kernspinresonanz plausibel macht.
Beim einfachsten Resonanz-Experiment, dem
Continous-Wave-Experiment (cw Abbildung
7) nutzt man diese Tatsache um durch das
langsame Ändern der Wellenlänge von eingestrahltem Licht irgendwann den Resonanzpeak zu nden und so Rückschlüsse auf z.B.
die Teilchenart machen zu können.
Figure 5: Die Netto-Magnetisierung als Vektorsumme der einzelnen Spins
tem, dass mit ωL rotiert, so dass in dem
neuen Koordinatensystem keine Bewegung
stattndet und können somit die Lage (und
für später wichtig: die Bewegung) der Nettomagnetisierung mit Hilfe der sogenannten
Bloch-Kugel zu beschreiben. (Abbildung 6)
Figure 7: Continous Wave Experiment
Figure 6: Bloch-Kugel
2.4
2.5
Resonanz
Relaxationszeiten
Wie oben bereits erwähnt existieren zwei Durch Einstrahlen eines transversalen MagSpineinstellungen, was in einem anliegenden netpulses kann man die Ausrichtung der
B-Feld zu einer Energieaufspaltung führt. Spins und somit des Magnetisierungsvektors
3
(siehe dazu nochmals Abbildung 6) ändern. die Spins, die nach einem Transversalpuls alle
Wählt man die Dauer des Pulses richtig so in Phase präzedieren brauchen, um wieder zu
ist es möglich ein Umklappen um beliebige dephasieren.
Winkel zu erzeugen. Zwei wichtige, weil in
der Praxis ständig angewandte Pulse sind der
90◦ - und 180◦ -Puls, die die Magnetisierung
dementsprechend um 90 bzw 180 Grad klappen. Da das longtudinale Magnetfeld (aucch
B0 -Feld genannt) jedoch nach wie vor anliegt richten sich die Spins nach und nach
wieder entlang der B0 -Feldlinien aus. Diesen
Vorgang bezeichnt man als Relaxation. Bei
der longitudinalen Relaxation betrachten wir
nur die z-Komponente der Magnetisierung
t
deren Änderung durch Mz = M0 (1 − e− T1 )
beschrieben wird (T1 ist hierbei die longituFigure 9: Transversale Relaxation
dinale Relaxationszeit). In Abbildung 8 ist
der zeitliche Verlauf der Änderung grasch
dargestellt. Die transversale Relaxation beIn der Praxis betrachtet man noch die
T 2∗ -Zeit, die Zeit des Free Induction Decay. Durch Inhomogenitäten im B0 -Feld und
lokal induzierte Felder von benachbarten Kernen kommt es dabei zu einer schnelleren Dephasierung (und somit Relaxation) der Spins,
als in der T 2-Zeit angenommen.
2.6
Bloch'sche
Bewegungs-
gleichung
Figure 8: Longitudinale Relaxation
Die oben beschriebenen Vorgänge lassen sich
alle durch die Bloch'schen Gleichungen ausdrücken. Diese wurden vom Nobelpreisträger
Felix Bloch als Bewegungsgleichungen für
den Magnetisierungsvektor eingeführt und
lauten:
trachtet nur die transversale Komponente der
Magnetisierung und ist beschrieben durch
− t
Mxy = Mxy0 e T2 (mit der transversalen Relaxationszeit T2)(Abbildung 9). Hierbei handelt es sich anschaulich um die Zeit, welche
4
Mit den Ergebnissen kann man Rückschlüsse
auf die chemische Struktur der betrachteten
dMx0
Mx0
Probe ziehen. In Abbildung 10 sind die ver= (ω0 − ω)My0 −
dt
T2
(1) schiedenen Resonanzfrequenzen der Kohlenstoatome je nach ihrer Verbindung im
dMy0
My0
Molekül zu sehen.
= (ω0 − ω)Mx0 + 2πγB1 Mz −
dt
T2
(2)
dMz0
Mz − Mz0
= −2πγB1 My0
dt
T1
(3)
3
Anwendungen
Mit den bisher vorgestellten Eigenschaften
der Kernspins im Feld, nämlich der der Resonanz und der Relaxationszeiten, haben wir
schon sehr viel von der Teilchenart und Umgebung abhängige Parameter gefunden.
Diese mikroskopischen Parameter können wir
durch Induktion (denn wir betrachten ja
insbesondere bei den Relaxationszeiten sich
zeitlich ändernde Magnetfelder) in messbare
elektrische Signale umwandeln und somit
auswerten. Zwei Anwendungen sind dabei
besonders hervorzuheben. Die Magnetresonanzspektroskopie und die Magnetresonanztomographie (MRT).
3.1
Figure 10: Chemische Verschiebung
3.2
MR-Tomographie
Bei der Magnetresonanztomographie werden
mit Hilfe der NMR Schnittbilder des (menschlichen) Körpers gewonnen. Dazu müssen
allerdings die empfangenen Signale räumlich
kodiert werden. Das geschieht mit Hilfe von
drei Gradientenspulen, deren Wirkungsweise
aus Bild 11 hervorgeht.
Die technische Umsetzung zeigt Bild 12.
Der supraleitende Magnet erzeugt das statische B0 -Feld, dessen Inhomogenitäten die
Shim-Spulen ausgleichen. Die Gradientenspulen erzeugen die Gradientenfelder und
die Körperspulen induzieren sowohl den B1 Puls, als wie sie auch die Relaxationssignale
aufnehmen.
NMR-Spektroskopie
Bei der NMR-Spektroskopie wird die Tatsache ausgenutzt, dass das Feld am Kernort immer von seiner Umgebung abhängig
ist. Man misst die Resonanzfrequenzen der
Teilchen einer Probe und bestimmt die relative Verschiebung der Resonanzfrequenzen
−νref
zur bekannten Eichfrequenz. δ = νP robe
νref
5
Figure 14: Bildrekonstruktion durch FT
Figure 11: Gradientenspulen zur räumlichen 4 Ausblick
Kodierung
Auch wenn die Grundlagen der NMR schon
lange bekannt sind, ist vor allem die Entwicklung der Bildgebung bei der MRT nach wie
vor ein hochaktuelles Feld und wird es auf
absehbare Zeit auch bleiben.
Figure 12: Technische Umsetzung
Die Bildrekonstruktion geschieht durch
Fouriertransformation der Signale, wobei
durch Manipulationen im Frequenzraum,
dem sogenannten k-Raum, noch einiges an
Qualitätsgewinn möglich ist. (Abbildung 13
und 14
Figure 13: Aufnahme der Signale im k-Raum
6