Höhere Experimentalphysik 1 - Goethe
Werbung

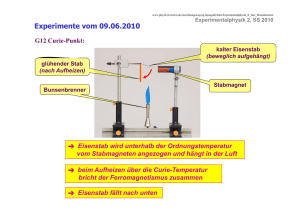
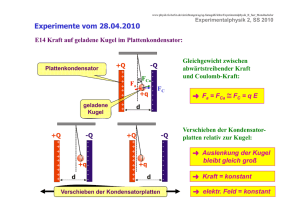
Höhere Experimentalphysik 1 Institut für Angewandte Physik Goethe-Universität Frankfurt am Main 5. Vorlesung 02.12.2016 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Ankündigung Übung Die nächste Übung findet am 21.12. statt! Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Was bisher geschah…. • Erzeugung von Magnetfeldern • Superpositionsprinzip • Einschluss in Magnetfeldern • • • • Solenoid Toroid Tokamak Stellerator • Materie in Magnetfeldern • Diamagnetismus • Paramagnetismus • Ferromagnetismus Felder und Potentiale von zwei Punktladungen Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Beispiel: Bennett-Pinch ohne mit Raumladungskompensation Willard Harrison Bennett 1903 - 1987 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Dielektrika Wie ein elektrisches Feld von Materie beeinflusst wird, hängt von ihrem atomaren Aufbau ab, speziell von Lage und Verschiebbarkeit der Ladungen darin. Dielektrika werden isolierende Stoffe bezeichnet, durch die das elektrische Feld „hindurchgreifen“ kann. Beobachtung: Eine Dielektrikum vergrößert Kondensators. Dazu wird die Dielektrizitätskonstante e eingeführt: die Kapazität eines Sie bezeichnet das Verhältnis der Kapazität des Kondensators mit diesem Isolator bzw. mit Vakuum im Plattenzwischenraum. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Polarisation Die freien Oberflächenladungen auf dem Dielektrikum schwächen das E-Feld und die Spannung bei gegebener Ladung der Platten, erhöhen also die Kapazität C= Q/U des Kondensators. Da das Feld an allen Atomen des Isolators in gleicher Weise angreift, werden deren negative Ladungen relativ zu den positiven verschoben. Genau wie bei der Influenz erzeugt diese Polarisation an den Oberflächen ein makroskopische Ladungsverteilung, die als Dipolmoment dargestellt werden kann. 0 d𝐩 = dV Dielektrische Suszeptibilität a ist die Polarisierbarkeit Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Elektrische Flussdichte Das resultierende elektrische Feld im Plattenkondensator mit Dielektrikum ist gegeben durch 𝑫 = 𝜀0 𝑬 + 𝑷 Im Fall des Vakuums verschwindet die Polarisation d.h. P=0. Mit zunehmender Feldstärke E spannen sich die Dipole auf oder orientieren sich durch das wirkende Drehmoment. Das geht zunächst linear los und sättigt bei höheren Feldstärken. Für den linearen Bereich gilt 𝑫 = 𝜀𝜀0 𝑬 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Polarisation • Verschiebungspolarisation: induzierte Dipole durch E-Felder, gesamte Probe stellt Dipol dar • Orientierungspolarisation: Dipolmomente sind bereits vorhanden aber aufgrund von Wärmebewegung regellos verteilt und werden erst in einem elektrischen Feld ausgerichtet Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Polarisierbarkeit von Atomen in elektrischen Wechselfeldern Da die Masse des positiven Atomkerns relativ schwer ist, werden durch das oszillierende Feld hauptsächlich Elektronen mit einer gewissen Schwingungsamplitude bewegt. Die Bewegungsgleichung der Elektronen im elektrische Wechselfeld Ex=E0xcos(wt) lautet dann Resonanzfrequenz w0/2p Die Lösung dieser Oszillatorgleichung ist mit Diese Auslenkung x entspricht eine oszillierendes Dipolmoment px=qx. Die Polarisierbarkeit a hängt also von der Frequenz des Wechselfeldes ab. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Polarisierbarkeit von Atomen in elektrischen Wechselfeldern Während die statische Polarisierbarkeit (w=0) beträgt, nimmt a in der Nähe der Resonanzfrequenz sehr viel höhere werte an und bei sehr hohen Frequenzen geht a gegen null, weil die Elektronen dem Feld nicht mehr folgen können. Beispiel: Die Suszeptibilität eines Plasma ist definiert als Mithilfe der Plasmafrequenz wird und man kann die Dielektrizitätskonstante aufgeschreiben zu Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Ionosphäre Reflexion bei f=fpe, Wellenausbreitung für f>fpe Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Faradaysches Induktionsgesetz Ein veränderlicher magnetischer Fluss durch eine Oberfläche induziert ein elektrisches Feld in jeder Grenzfläche dieser Oberfläche, und ein veränderliches Magnetfeld induziert ein zirkulierendes elektrisches Feld. M. Faraday, 1831 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Faradaysches Induktionsgesetz Laborsystem Ein Draht fliegt durch ein B-Feld und die Lorentz-Kraft treibt Ladungen nach rechts bis ein Gegenfeld : 𝑞𝑬′′ = −𝑭 = −𝑞𝒗 × 𝑩 erzeugt wird. Bezugssystem Es herrscht ein Feld B, quer dazu ein Feld 𝑬′ = 𝑣 × 𝑩, das durch 𝑬′′ = −𝑣 × 𝑩 kompensiert wird. Die Drahtschleife durch ein homogenes B-Feld. Die E-Felder in den beiden zweigen kompensieren sich. Es entsteht keine Gesamtspannung. Es herrscht ein B-Feld, quer dazu ein EFeld, beide sind homogen. Ein Voltmeter schlägt nicht aus. Die Drahtschleife durch ein inhomogenes B-Feld. Die E-Felder in den beiden zweigen kompensieren sich nicht. Es entsteht eine Gesamtspannung: 𝑈 = 𝑬′ ∙ 𝑑𝑟 = −𝑎 𝐸2 − 𝐸1 B steigt zeitlich an. Es entsteht eine Spannung: 𝑑𝐵 𝑈 = −𝑎𝑏𝑣 = −𝑎𝑏𝐵 𝑑𝑦 𝑈 = −𝜙 = −𝑎𝑣 𝐵2 − 𝐵1 = −𝑎𝑣𝑏 𝑑𝐵 𝑑𝑦 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Versuch: Induktion Wirbelfeld auf einem rotierenden Zylinder im Erdmagnetfeld Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Versuch: Induktion Das gemessene Erdmagnetfeld hatte eine Stärke von: BErd = 56 G. Im ungeschlitzten Zylinder wurde ein Magnetfeld von BInd = 0,06 G erzeugt. Im geschlitzten Zylinder baute sich kein Magnetfeld auf, da die Wirbelströme durch die Schlitze unterbrochen wurden. Höhere Experimentalphysik 1 IAP Anwendungen Der Transformator Goethe-Universität Frankfurt am Main Das Betatron Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Elektromagnetische Wellen • Ruhende elektrische Ladungen erzeugen elektrische Felder, deren Feldlinien in den Ladungen beginnen oder enden: • Der Gesamtfluss durch eine geschlossenen Oberfläche ist Null. • Ströme d.h. bewegte Ladungen, erzeugen Magnetfelder, deren geschlossenen Feldlinien die Ströme umkreisen • Sich ändernde Magnetfelder erzeugen elektrische Felder, deren geschlossene Feldlinien die Änderungsrichtung des Magnetfeldes umkreisen 𝐸 ∙ 𝑑𝑠 = − 𝜕𝐵 ∙ 𝑑𝐴 𝜕𝑡 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Das Amperesche Gesetz Im Ampereschen Gesetz wird ausgesagt, dass jeder Leitungsstrom I von magnetischen Feldlinien umgeben ist: Erweiterung durch Maxwell 1850 Das bedeutet, das Linienintegral über einen beliebigen, geschlossenen Integrationsweg C ist gleich mal dem vom Integrationsweg eingeschlossenen Strom I: Magnetfelder werden von bewegter Ladung erzeugt. Maxwell wies als Erster darauf hin, dass das Gestz in dieser Form bei Wechselstromkreisen mit Kondensator keine eindeutigen Werte von liefert. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Das Amperesche Gesetz - Erweiterung Leitungsstrom in den Kondensator: Wenn man nun auf der rechten Seite von den von der elektrischen Feldstärke abhängigen sogenannten Verschiebungsstrom addieren, erhalten wir in beiden Fällen dieselbe magnetische Feldstärke. Der Verschiebungsstrom ist allgemein gegeben durch Integration über E dA: Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Das Ampere-Maxwellsche Gesetz Ein elektrischer Strom oder ein veränderlicher elektrisches Fluss durch eine Oberfläche produziert ein zirkulierendes magnetisches Feld um jeden Pfad der diese Fläche begrenzt. Integralform: Differentielle Form: Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Das Ampere-Maxwellsche Gesetz Ein veränderliches elektrisches Feld erzeugt ein veränderliches Magnetfeld auch wenn keine Ladungen vorhanden sind und kein Strom fließt. Durch diesen Mechanismus (d.h. veränderliche elektrische Felder induzieren Magnetfelder, veränderliche Magnetfelder induzieren elektrische Felder usw.) können elektromagnetische Wellen selbst durch ein perfektes Vakuum propagieren. Das Einbeziehen des Verschiebungsstroms in das Amperesche Gesetz war der bedeutende Schritt, der es Maxwell erlaubte die bekannten elektromagnetischen Gleichungen zu einer Wellengleichung zu kombinieren und somit „eine dynamische Theorie des elektromagnetischen Feldes“ zu entwickeln. Das Magnetfeld einer freien elektromagnetischen Welle rührt nur vom Verschiebungsstrom! Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Elektromagnetische Wellen Nachdem Maxwell die Existenz von elektromagnetische Wellen vorhergesagt hatte, gelang um 1860 Heinrich Hertz erstmals die Erzeugung von Radiowellen und der Nachweis, dass sie sich mit der Lichtgeschwindigkeit ausbreiten. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Wellengleichungen Bildet man in der zweiten Maxwell Gleichung die Rotation, d.h. (1) mit der Operatoridentität (2) folgt (3) Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Wellengleichungen Die Rotation des Magnetfeldes ist gegeben durch (4) Somit kann man (3) ausdrücken durch (5) Mithilfe des Gaußschen Gesetzes wird aus (5) Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Wellengleichungen Durch das Umstellen der Terme, die das elektrische Feld enthalten folgt (6) Im Fall von ladungs-und stromfreier Region gilt (7) Ebenso lässt sich aus dem Ampereschen Gesetz die Wellengleichung für das Magnetfeld ableiten (8) Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Wellengleichungen Diese Wellengleichungen sind partielle Differentialgleichungen von zweiter Ordnung mit jeweils drei Feldkomponenten. Sie beschreiben elektromagnetische Wellen, die sich z.B. im freien Raum mit Lichtgeschwindigkeit c ausbreiten. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Wellengleichungen Mit den Lösungsansatz einer transversal ebene Welle zeigt sich, dass das elektrische Feld und das magnetische Feld am gleichen Ort und zur gleichen Zeit ihr Maximum erreichen d.h. E und B sind in Phase. Nahfeld E- und B-Feld phasenverschoben um 90° Bildquelle: http://www.meteo.physik.uni-muenchen.de /lehre/crewell/vorles/FE_vorles/FE_29okt04.pdf Fernfeld E- und B-Feld in Phase Bildquelle: http://de.sci.physik.narkive.com/s0TWg3yW/nah-und-fernfeld-von-dipolstrahlung-phasenverschiebung:i.1.1.full Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Erzeugung von EM-Wellen – Hertzscher Dipol Felder sind zunächst im Inneren von Kondensator bzw. Spule konzentriert. Allerdings ändert sich das mit Form des Schwingkreises und die Felder reichen weit nach außen. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Beispiel: Abstrahlcharakteristiken Polar Plot Polar Plot 90 90 120 120 60 0,6 0,8 0,6 150 30 150 30 0,4 0,2 0,4 0,2 0,1 0,2 0,0 0,4 60 0,3 30 0,6 120 0,4 150 0,8 1,0 60 0,8 1,0 90 0,5 1,0 180 Polar Plot 0,2 0 0,0 0,2 0,4 0,6 0,8 1,0 180 0,0 0,5 0,4 0,3 0,2 0,2 0,1 0 0,0 0,1 0,2 0,3 0,4 0,5 180 0,0 1,0 0,8 0,6 0,1 0,4 0,2 0 0,0 0,2 0,4 0,6 0,8 1,0 0,2 0,4 0,2 210 0,4 330 210 0,6 330 210 330 0,3 0,6 0,4 0,8 0,8 240 300 1,0 270 240 300 0,5 270 Die rechte Antenne eilt um T/2 nach Die rechte Antenne eilt um T/4 nach 240 300 1,0 270 Schwingen in Phase Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Energiedichte einer elektromagnetischen Welle Die Energiedichte w der Welle setzt sich aus einem elektrischen und einem magnetischen Anteil zusammen: Wegen folgt =ExB Energiestromdichte S ist gegeben durch und zeigt ebenfalls räumlich periodische Schwankungen wie E und B. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Poynting-Vektor Der Poynting-Vektor (abgeleitet für eine ebene Welle) zeigt in die Ausbreitungsrichtung und sein Betrag gibt die Intensität der elektromagnetischen Welle an: Ganz allgemein gibt der Poynting Vektor den Energiestrom im elektromagnetischen Feld wieder.