Höhere Experimentalphysik 1 - Goethe
Werbung
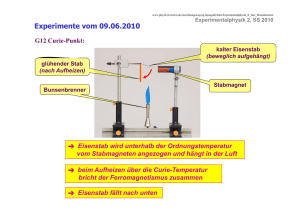
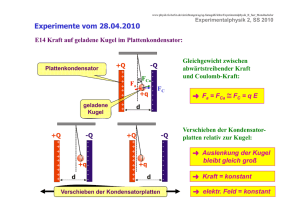
Höhere Experimentalphysik 1 Institut für Angewandte Physik Goethe-Universität Frankfurt am Main 3. Vorlesung 18.11.2016 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Was bisher geschah…. • Bewegte Ladungen • Strom • Gaußsches Gesetz für Magnetfelder • Amperesches Gesetz • Bewegte Ladung im Magnetfeld • Lorentz-Kraft Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Was bisher geschah…. Gesetz von Biot-Savart Anhand der Stromverteilung kann die magnetische Feldverteilung berechnet werden. Der Beitrag dB zum Magnetfeld am Punkt P erzeugt durch einen kleinen elektrischen Strom ist gegeben durch das Biot-Savart-Gesetz: m r dl ist ein Element entlang des Drahtes und r ist der Vektor zwischen Anfangspunkt und zum Punkt m. Man teilt den stromführenden Draht in kurze Elemente dl und berechnet den Feldbetrag dB des Leiterelements an einer Stelle im Abstand r. B steht überall senkrecht auf r und dl. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Was bisher geschah… Felder bewegter Ladungen am Beispiel eines Elektronenstrahls mit homogener Ladungsträgerdichte π π ππ = = 2 π ο°π π0 π£π§ β« π£π₯,π¦ Aus der Lorentz-Kontraktion folgt Ladungsträgerdichte im Laborsystem: π = π0 ο§−1 π ππ = 2 ο°π πΎπ ππ,0 · ππ΄ πΌ πΈ0 = = 2ο°ο₯0 π 2ο°ο₯0 π£π§ π geschwindigkeitsabhängige πΈ = ο§πΈ0 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Anwendung von Helmholtz-Spulen - Kompensation des Erdmagnetfeldes z.B. Karlsruher Tritium Neutrino Experiment (KATRIN) - COLTRIMS magnetisches Führungsfeld - Partikelfallen Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Magnetische Flasche / magnetischer Spiegel Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Magnetische Flasche / magnetischer Spiegel Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Magnetische Fokussierung geladene Teilchen mit π£β₯ β« π£⊥ Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Solenoid Am Rand ist π΅π ≠ 0 π£π§ × π΅π → πΉπ Kick verursacht vf Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Fokussierung mit Solenoid Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Vom Solenoid zum Toroid Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Magneteinschluß - Tokamak ΡΠΎΡΠΎΠΈΠ΄Π°Π»ΡΠ½Π°Ρ ΠΊΠ°ΠΌΠ΅ΡΠ° Π² ΠΌΠ°Π³Π½ΠΈΡΠ½ΡΡ ΠΊΠ°ΡΡΡΠΊΠ°Ρ Andrei D. Sacharow Igor J. Tamm (1921 - 1989) (1895 - 1971) Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern International Thermonuclear Experimental Reactor Zentrale Solenoid Nb3Sn, 6 Modulen Blanket Poloidale Spulen Nb-Ti Divertor Toroidale Spule Nb3Sn Kryopumpen,8 Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Magneteinschluß - Stellerator Lyman Spitzer, Jr. (1914 - 1997) Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einschluss in Magnetfeldern Stellarator Wendelstein 7-X großer Plasmaradius 5.5 m kleiner Plasmaradius 0.53 m Entladungsdauer 30 min Plasmaheizung 14 MW Magnetfeld 3.45 T Plasmamasse 5-30 mg Plasmatemperatur 6-13 keV Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Fadenstrahlröhre Erzeugung eines Elektronenstrahles π · πΈ = ππ ·π π=π πΈππ π = ππ 1 ππ = ππ π£ 2 2 s π£= (1) Glühfilament (2) Wehnelt-Zylinder (3) Lochblende 2ππ ππ πππ Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Fadenstrahlröhre Bewegungsgleichung eines Elektrons im magnetischen Feld Lorentz - Kraft Magnetfeld in z - Richtung ππ π£ = ππ£ π₯ π΅ π π£π₯ = π£π¦ π΅ ππ π π£π¦ = − π£π₯ π΅ ππ (1) (2) π£π§ = 0 π 2 π£π₯ ππ΅ = − ππ‘ 2 ππ (3) 2 π£π₯ ππ΅ ππ΅ π£π₯ = π1 cos π‘ + π2 sin π‘ ππ ππ (1) nach der Zeit ableiten und (2) einsetzen Lösung für vx; vy entsprechend Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Fadenstrahlröhre Kräftegleichgewicht bei der Bewegung eines Elektrons im magnetischen Feld Zentrifugalkraft πΉπ = πΉπΏ ππ π£ 2 = evB π π π΅= ππ Lorentz - Kraft im mitrotierenden Bezugssystem 2ππππ π΅= ππ 1 ππ π΅ = 2π π π Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Fadenstrahlröhre Experimenteller Aufbau Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Fadenstrahlröhre Ergebnisse Beispiel LHC CERN e C ο½ 1,758 ο1011 me kg r = 3cm U = 400V e C ο½ 9,578 ο107 mp kg u = 26,659 km B = 2,25mT Entspricht einem Spulenstrom von ISpule = 3A r = 4243 m B = 63,7mT ? U = 3,5TV = 3,5·1012V Protonen bewegen sich mit nahezu Lichtgeschwindigkeit, deshalb: relativistische Massenzunahme Faktor 7000 B = 5,28T Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Stromdurchflossener Leiter im Magnetfeld Ladungsträgertransport im Magnetfeld ππ π£ = ππ£ π₯ π΅ Lorentz - Kraft auf die ne lA Elektronen im Draht πΉ = −πππ ππ΄π£ π₯ π΅ πΉ = πΌπ π₯ π΅ πΉ =ππ₯π΅ - Unabhängig von mikroskopischen Gegebenheiten des Ladungstransports - Unabhängig vom Vorzeichen der Ladung - Unabhängig von der Anzahl verschiedener Ladungsträgergruppen und deren Geschwindigkeit, denn F ist proportional zum Strom Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Stromwaage Gewichtskraft ππ = ππ£ π₯ π΅ FL- FG πΉπΊ = πΌπ π₯ π΅ πΉπΊ π΅= πΌπ Lorentz - Kraft Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Elektrische und magnetische Felder in Materie Materie im Magnetfeld - das magnetische Moment Das magnetische Moment immer gemeinsam mit einem Bahndrehimpuls L auf. Messung des magnetischen Moments durch das Stern-Gerlach Experiment: Auf einen magnetischen Dipol wirkt im inhomogenen Magnetfeld eine Ablenkkraft, die ihren größten Wert F=m gradB für die Dipole erreicht die antiparallel zum Feld orientiert sind. Daher lässt sich bei bekanntem Feldgradienten aus dem maximalen Ablenkwinkel des Atomstrahls das atomare magnetische Moment bestimmen. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Einstein de Haas Effekt Makroskopischer Nachweis des Elektronenspins Bei der Magnetisierung ändert sich der Spin der Elektronen in einem Material. Da der Spin aber ein Drehimpuls ist und der Gesamtdrehimpuls erhalten ist, wird die Drehimpulsänderung durch die Spinausrichtung durch eine Drehung des Körpers kompensiert. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Magnetisierung der Materie Magnetisierung und Suszeptibilität Die Ausrichtung magnetischer Dipole in einem Material unter der Einwirkung eines äußeren Feld H führt zu einer Magnetisierung. Man definiert die Magnetisierung M mittels ππ π΄= ππ als magnetisches Dipolmoment je Volumeneinheit. Die Magnetisierung addiert sich zum äußeren Feld, und man erhält als Summe die magnetische Flussdichte π© = π0 (π― + π΄) Die Einheit von B ist das Tesla (T) mit 1 T = 1 Vs/m2 . Der Vorfaktor µ0 bezeichnet die Permeabilität des Vakuums Die magnetische Suszeptibilität (v. lat. susceptibilitas „Übernahmefähigkeit“) ist eine einheitenlose physikalische Größe, die die Magnetisierbarkeit von Materie in einem externen Magnetfeld angibt. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Die Magnetisierung der Materie Magnetisierung und Suszeptibilität Im Vakuum, wo es keine Magnetisierung M gibt, kann man H und B als wechselseitig aufeinander skalierbare Größen betrachten. In Materie dagegen ergibt sich π© = π0 π― + ππ π― = π0 1 + ππ π― = π0 ππ π― ππ ist die magnetische Suszeptibilität, die die Magnetisierbarkeit von Materie in einem externen Magnetfeld angibt. An Hand der Suszeptibilität kann eine erste Einteilung der verschiedenen magnetischen Phänomene gegeben werden Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Diamagnetismus (ο£ <0 ) Im diamagnetischen Atom ist die Summe aller magnetischer Momente der Elektronen exakt null. π= ππ = 0 π Jede Elektronenbahn ist von zwei gegenläufigen Elektronen besetzt. Ein diamagnetisches Atom hat deshalb, ohne äusseres B-Feld eine kugelsymmetrische Ladungsverteilung. Diese entsteht, weil sich die einzelnen Elektronenbewegungen über die Zeit ausmitteln. Wenn ein B-Feld eingeschaltet wird, beginnt diese kugelsymmetrische Ladungsverteilung mit der Larmorfrequenz ππ΅ π= π zu präzedieren. Durch diese Präzession im Magnetfeld entsteht ein von null verschiedenes magnetisches Moment m , das zum Diamagnetismus führt. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Paramagnetismus (ο£ > 0 ) Besitzt ein Atom bzw. Molekül bereits ein permanentes Dipolmoment (π ≠ 0), so wird es in einem äußeren Feld ausgerichtet. Die Überlagerung der Dipolmomente vieler Moleküle führt zu einer Magnetisierung, die das äußere Feld verstärkt. Es gilt ο£ > 0 bzw. ο > 1. Solche Stoffe bezeichnet man als paramagnetisch. Man unterscheidet: • Atomaren Paramagnetismus: Er rührt von Atomen oder Molekülen mit teilweise gefüllten Schalen her. Die Suszeptibilität ist temperaturabhängig gemäß πΆ ππ = π π2 wobei πΆ = π0 π 3ππ΅ die Curie-Konstante ist. • Paramagnetismus der Leitungselektronen: Die sich in einem Metall frei bewegenden Ladungsträger besitzen durch ihren Spin ein permanentes magnetisches Moment. Dieser sogenannte Pauli-Paramagnetismus hängt nicht von der Temperatur ab. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Ferromagnetismus Hysterese-Kurve In einem ferromagnetischen Material (Eisen) existieren so genannte Weisssche Bezirke, in denen die atomare magnetische Momente parallel ausgerichtet sind. Ohne äußeres Magnetfeld sind sind die Magnetisierungsrichtungen dieser Bereiche statistisch verteilt und heben sich makroskopisch auf, so dass die Probe nicht magnetisch erscheint. Erhöht man die äußere Feldstärke, so wachsen nicht nur die Weissschen Bezirke, sie richten sich nun auch parallel zum äußeren Feld aus. Die Magnetisierung wächst an bis ein Sättigungszustand eintritt, da alle magnetische Moment der Probe nun parallel zum Feld ausgerichtet sind. Bei abnehmendem äußeren Magnetfeld dreht sich die Magnetisierungsrichtung der Weissschen Bezirke wieder in ihre ursprüngliche Richtung, es bleibt aber bei nicht vorhandenem äußeren Feld eine Restmagnetisierung übrig. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Ferromagnetismus Die ferromagnetischen Eigenschaften gehen jedoch verloren, wenn die CurieTemperatur TC überschritten wird, das Material wird dann paramagnetisch. Analog zum Curie-Gesetz beim Paramagnetismus gilt beim Ferromagnetismus das Curie-Weiss-Gesetz: πΆ π= π−Θ Bei ferromagnetischen Stoffen weicht die Kurve vom Curie-Weiss-Gesetz in der Nähe von Θ ab und geht erst bei TC durch Null. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Dielektrika Wie ein elektrisches Feld von Materie beeinflusst wird, hängt natürlich von ihrem atomaren Aufbau ab, speziell von Lage und Verschiebbarkeit der Ladungen darin. Dielektrika werden isolierende Stoffe bezeichnet, durch die das elektrische Feld „hindurchgreifen“ kann. Beobachtung: Eine Dielektrikum vergrößert die Kapazität eines Kondensators. Dazu wird die Dielektrizitätskonstante ο₯ eingeführt: Sie bezeichnet das Verhältnis der Kapazität des Kondensators mit diesem Isolator bzw. mit Vakuum im Plattenzwischenraum. Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Polarisation Die freien Oberflächenladungen auf dem Dielektrikum schwächen das E-Feld und die Spannung bei gegebener Ladung der Platten, erhöhen also die Kapazität C= Q/U des Kondensators. Da das Feld an allen Atomen des Isolators in gleicher Weise angreift, werden deren negative Ladungen relativ zu den positiven verschoben. Genau wie bei der Influenz erzeugt diese Polarisation an den Oberflächen ein makroskopische Ladungsverteilung, die als Dipolmoment dargestellt werden kann. 0 Dielektrische Suszeptibilität Höhere Experimentalphysik 1 IAP Goethe-Universität Frankfurt am Main Polarisation • Verschiebungspolarisation: induzierte Dipole durch E-Felder • Orientierungspolarisation: Dipolmomente sind bereits vorhanden aber aufgrund von Wärmebewegung regellos verteilt und werden erst in einem elektrischen Feld ausgereichtet
