Physik I+II Formelsammlung - rohde

Formelsammlung Physik I & II
für Studenten der Elektrotechnik
Umfangreiche Formelsammlung analog zur
Physikvorlesung von Prof. Dr. K. Röll für
das erste und zweite Semester
Hinweise auf werksmäßig
eingespeicherte und sonstige
empfehlenswerte TI-Konstanten
Holger Hafke
Andreas Kördel
Stefan Rohde
© 20 03
Inhaltsverzeichnis
2. Eindimensionale Bewegung
2.1 Weg, Geschwindigkeit, Beschleunigung (bei konstanter Kraft)
2.2 Newton Gesetze
2.3 Schiefe Ebene
2.6 Bewegung bei linearer Kraft (Federschwingung)
4
4
4
4
4
3. Energie (Feder)
3.1 mechanische Arbeit
3.2 kinetische und potentielle Energie
3.3 Energieverwaltung
3.4 Energiebilanz der Schwingung
5
5
5
5
5
4. Satelliten und Planeten
4.1 Gravitation
4.3 Bewegung auf Kreisbahnen
4.4 Planeten- und Satellitenbahnen
4.5 Energie auf Satellitenbahnen
6
6
6
6
7
5. Elektrische und magnetische Felder
5.1 Elektrisches Feld
5.2 Energie im elektrischen Feld
5.3 Magnetfelder
8
8
8
8
6. Elektronen und Ionenstrahlen
6.1 Bewegung (parallel) im homogenen elektrischen Feld
6.2 Zweidimensionale Bewegung / Wurf
6.3 Ablenkung im elektrischen Feld
6.4 Energieaufnahme im elektrischen Feld
6.5 Ablenkung im Magnetfeld
9
9
9
9
10
10
7. Impuls
7.1 Impulserhaltung:
7.2 Raketenantrieb
7.3 Stoßvorgänge
11
11
11
11
8. Relativitätstheorie
8.1 Lichtausbreitung / Geschwindigkeit
8.2 Zeitdilatation
8.3 Relativistische Masse & Energie
8.4 Raum und Zeit:
13
13
13
13
13
9. Schwingungen
9.1 Darstellung
9.2 Mechanische & elektrische Schwingungen
9.4 Erzwungene Schwingung, Resonanz
14
14
14
15
10. Wellen
10.1 Darstellung von Wellen
10.2 Wellenphänomene: Schall und Licht
10.3 Ausbreitung von Wellen
10.4 Interferenz
10.5 Dopplereffekt
10.7 Beugung
16
16
16
17
17
18
18
11. Wellen und Quanten
11.1 Thermische Strahlung
11.4 Lichtelektrischer Effekt
11.5 Welle-Teilchen:
19
19
19
20
Universität Kassel - Formelsammlung Physik I+II
2
© H.Hafke, A.Kördel, S.Rohde 2003
12. Atombau
12.1 Bohr-Atommodell
12.2 Energie-Übergänge
12.3 Röntgenstrahlung
21
21
21
21
13. Physik der Gase
13.1 Temperatur und Wärmeenergie
13.2 Atome und Moleküle
13.2 Thermische Energie der Gase
13.4 Zustandsgleichung des idealen Gases
13.5 p-V-Diagramm
22
22
22
22
23
23
14. Thermodynamik
14.1 Mechanische Arbeit
14.2 Energieerhaltung (1.Hauptsatz)
14.4 Wärmekraftmaschine
14.5 Kreisprozesse:
14.6 Reale Gase:
24
24
24
25
25
26
15. Ti-Konstanten
27
Universität Kassel - Formelsammlung Physik I+II
3
© H.Hafke, A.Kördel, S.Rohde 2003
2. Eindimensionale Bewegung
2.1Weg, Geschwindigkeit, Beschleunigung (bei konstanter Kraft)
Weg:
a
s (t ) = s0 + v0 ⋅ t + ⋅ t 2
2
Geschwindigkeit:
v(t ) = s&(t ) = v0 + a ⋅ t
Beschleunigung:
a (t ) = v&(t ) = &&
s (t ) = a =
Freier Fall:
1
h(t ) = h0 − ⋅ g ⋅ t 2
2
s0 = Anfangsweg
v=
∆s
∆t
v0 = Anfangsgeschwindigkeit
F
m
h0 = Anfangshöhe
g=_ g
2.2 Newton Gesetze
Wurf nach oben:
1 v2
su = ⋅ 0
2 g
Schwerkraft:
Fg = − m ⋅ g
tu =
v0
g
u = Umkehrpunkt
Wurf
2.3 Schiefe Ebene
sin α =
(Bewegung bei konstanter Kraft)
S.12
1.2.4
geg
an
geg
, cos α =
, tan α =
hyp
hyp
an
F = m ⋅ g ⋅ sin α
⎧ s0 = 0
⎪
Spezialfall ⎨
v2
s
=
⎪
2 ⋅α
⎩
v0 = 0
s
v0 = 2 ⋅ a ⋅ s
F
FG
α
2.6 Bewegung bei linearer Kraft
(Federschwingung)
Ruhelage:
F0 = m ⋅ g
Auslenkung:
F = −D ⋅ y
(Rücktreibende Kraft)
Fg = ( F0 − D ⋅ y ) − m ⋅ g
Schwingung:
y = y0 ⋅ cos(ω ⋅ t − ϕ )
D = Federkonstante
ω2 =
D
m
v = y& = − y0 ⋅ ω ⋅ sin(ω ⋅ t )
a = &&
y = − y0 ⋅ ω 2 ⋅ cos(ω ⋅ t )
Universität Kassel - Formelsammlung Physik I+II
4
vmax = ω ⋅ y0
© H.Hafke, A.Kördel, S.Rohde 2003
3. Energie (Feder)
3.1 mechanische Arbeit
in s-Richtung bei konstanter Kraft
W = ( F ⋅ cos α ) ⋅ s
bei nicht konstanter Kraft
Wab = ∫ ( F ⋅ cos α ) ⋅ ds = ∫ 1dW
b
W
a
0
1
W = ⋅ D ⋅ x2
2
Arbeit beim Dehnen einer Feder:
F0cos α
Wab
a
ds
s
b
3.2 kinetische und potentielle Energie
g=_ g
kinetische Arbeit:
1
⋅ m ⋅v2
2
W12 = Ek ( 2) − Ek (1)
potentielle Energie:
Ep = m⋅ g ⋅ z
potentielle Arbeit:
W12 = E p ( 2) − E p (1)
1
E p = ⋅ D ⋅ x2
2
Ek =
kinetische Energie:
potentielle Energie der Feder:
3.3 Energieverwaltung
Abgeschlossenes System → Energie bleibt erhalten
E = Ek + E p + Q
(2)
Q12 = − ∫ FR ⋅ ds
Reibung :
(1)
konstante Reibung:
Q = − FR ⋅ s
3.4 Energiebilanz der Schwingung
y = y0 ⋅ cos(ω⋅ t)
1
E P = D ⋅ y2
2
m
E K = ⋅ v0 2
2
Universität Kassel - Formelsammlung Physik I+II
E = EP + EK
F = −D ⋅ y
ω= D/m
5
© H.Hafke, A.Kördel, S.Rohde 2003
M
4. Satelliten und Planeten
m
4.1 Gravitation
r
M ⋅m
r2
im Raum / Newton:
F = −G ⋅
Nahe der Erdoberfläche:
F = − m ⋅ g = −G ⋅
für kugel- oder punktförmige Massen
M ⋅m
RE 2
Æ
g = G⋅
M
r2
G=_ gc
4.3 Bewegung auf Kreisbahnen
s = r ⋅ ϕ (t )
ϕ& = ω
v = s& = r ⋅ ϕ& (t )
v = r ⋅ω
ω=
2 ⋅π
T
vconst =
2 ⋅π ⋅ r
T
volle Umdrehung
v2
= −m ⋅ω 2 ⋅r
r
Zentripetalkraft:
Fz = −m ⋅
Rotationsenergie:
1
Erot = ⋅ I ⋅ ω 2
2
Trägheitsmoment :
I = m ⋅ r2
für Punkt
I=
1
m⋅ r2
2
für Scheibe
I=
2
m⋅ r2
3
für Kugel
4.4 Planeten- und Satellitenbahnen
G⋅M
r
Kreisbahn:
vk =
Umlaufzeit:
T=
3. Kepler Gesetz:
⎛ T2 ⎞ ⎛ r2 ⎞
⎜ ⎟ =⎜ ⎟
⎝ T1 ⎠ ⎝ r1 ⎠
Fluchtgeschwindigkeit:
vF = 2 ⋅ vk =
erdnah : vE =
2⋅π ⋅ r
r3
= 2 ⋅π ⋅
vk
G⋅M
2
Universität Kassel - Formelsammlung Physik I+II
3
G⋅ME
RE
merde
mmond
rerde
2 ⋅G ⋅M
r
6
© H.Hafke, A.Kördel, S.Rohde 2003
4.5 Energie auf Satellitenbahnen
M
potentielle Energie:
kinetische Energie:
Fluchtenergie:
Gesamtenergie:
Meteorit auf Erde:
Satellit zur Kreisbahn:
M ⋅m
E p = −G ⋅
r
1
m
Ek = ⋅ E p = v 2
2
2
m 2
M⋅m
⋅ v ≥ G⋅
2
r
1
Eg = ⋅ E p
2
vend
m
r
G=_ gc
G ⋅ME
= v0 + 2 ⋅
RE
2
+
EPotB
+
EPotA
KinB
KinA
⎛6
⎞ ⎛6
⎞
4E7
4
8 64748
4E74
8 64748
⎜m
⎟
⎜
⎟
M
⋅
m
m
M
⋅
m
2
2
E
E
⎜ ⋅ vKB −G ⋅
⎟ − ⎜ ⋅ vOFL −G ⋅
⎟

RE + h ⎟ ⎜ 2  
RE ⎟
⎜⎜ 2
*
⎟ ⎜
⎟
⎝1444
424444
3⎠ ⎝1444
424444
3⎠
EEnde
E Anfang
* kann vernachlässigt werden
2
Abschuss in Weltraum zum Punkt R: v0 ≥ 2 ⋅
Universität Kassel - Formelsammlung Physik I+II
G⋅M
= 2 ⋅ vK 2
R
7
© H.Hafke, A.Kördel, S.Rohde 2003
5. Elektrische und magnetische Felder
5.1 Elektrisches Feld
Kugel:
F = q⋅E
Q
1
E=
⋅ 2
4 ⋅π ⋅ε 0 r
Q = C ⋅U 0
ε ⋅A
C= 0
d
U
Q
(homogen)
EKond = 0 =
d ε0 ⋅ A
C = 4 ⋅π ⋅ε0 ⋅ R
Dipolmoment:
Q = 4 ⋅ π ⋅ ε 0 ⋅ R ⋅U 0
Q
R
E=
= U0 ⋅ 2
2
r
4 ⋅π ⋅ε0 ⋅ r
r
r
p = Q⋅a
Coulomb-Kraft:
Coulomb Feldstärke:
Plattenkondensator:
Feldstärke:
a = Abstand
ε0=_ε0
5.2 Energie im elektrischen Feld
homogenes Feld:
U=
U0
⋅y
d
⎛ U ⎞
W12 = ⎜ q ⋅ 0 ⎟ ⋅ y = q ⋅ ∆U
⎝ d ⎠
potentielle Energie:
Ep = q ⋅U
Kugel:
Ep =
1
4 ⋅π ⋅ε0
⋅
Q⋅q
R⎞
⎛
= q ⋅U = q ⋅⎜ U 0 ⋅ ⎟
r
r⎠
⎝
5.3 Magnetfelder
im Vakuum:
r
r
B = µ0 ⋅ H
gerader Draht:
H=
I
B=
FB
q⋅v
Schleife:
Spule:
2 ⋅π ⋅ r
I
H=
2⋅ r
N
H =I⋅
l
µ = I ⋅ π ⋅ r2
Universität Kassel - Formelsammlung Physik I+II
8
© H.Hafke, A.Kördel, S.Rohde 2003
6. Elektronen und Ionenstrahlen
6.1 Bewegung (parallel) im homogenen elektrischen Feld
Schwebezustand:
Bewegte Ladung:
q=
m⋅ g m⋅ g
=
⋅d
E
U
E=
U0
d
v=
F = q⋅E
a=
q⋅E
m
a2 ⋅ 2 ⋅ x
q⋅E
2 ⋅ q ⋅ ∆U
= 2⋅
⋅x =
a
m
m
E pot = q ⋅ U
1
Ekin = ⋅ m ⋅ v 2
2
6.2 Zweidimensionale Bewegung / Wurf
Schiefe Ebene:
x = v0 x ⋅ t
1
y = y0 + y0 y ⋅ t − ⋅ a ⋅ y ⋅ t 2
2
2
Parabelgleichung:
⎞ ⎛ x ⎞
⎛v ⎞
1 ⎛
y ( x) = y0 + ⎜ 0 y ⎟ ⋅ x − ⋅ ⎜ g ⋅ sin γ{ ⎟ ⋅ ⎜
⎟ v ⎟
v0 x ⎠
2 ⎜⎝
0x ⎠
⎝{
90° ⎠ ⎝
{
tan(α )
Schiefer Wurf:
v0 =
t
g ⋅ x2
2 ⋅ cos 2 (α ) ⋅ (x ⋅ tan(α) − ∆y)
90
}°
g ⋅ sin γ
⋅x
2⋅ z
Horizontaler Wurf (speziell):
v0 =
Kreisbahn:
α = ω −t
∆y = x ⋅ tan(α) −
z = y(x) − y0
Wurf
g ⋅ x2
2 ⋅ v0 2 ⋅ cos 2 (α)
S.12
1.2.4
6.3 Ablenkung im elektrischen Feld
Ablenkung:
t ⎞
E ⎛}
}
q U ⎜ x2 ⎟
⋅ ⋅⎜
y ( x) = −
⎟
2 ⋅ m d ⎜ v0 2 ⎟
⎜
⎟
⎝
⎠
Austrittswinkel:
tan γ = −
Energieanalysator:
v0 =
2
Universität Kassel - Formelsammlung Physik I+II
q U L
⋅ ⋅
m d v0 2
q=_q
x=L
q U
⋅
⋅L
m d2
9
© H.Hafke, A.Kördel, S.Rohde 2003
6.4 Energieaufnahme im elektrischen Feld
1
1
⋅ m ⋅ v12 + q ⋅ U1 = ⋅ m ⋅ v2 2 + q ⋅ U 2
2424
2424
1
3
1
3
Ekin
Ekin
1442443 144
2443
vorher
Ladung e im Feld:
nachher
Ekin = e ⋅ ∆ U
6.5 Ablenkung im Magnetfeld
r
r r
F = I × B ⋅ l , F = ( I ⋅ B ⋅ sin α ) ⋅ l
(
r
)
r
r
Kraft auf einzelne Ladung (Lorentz-Kraft): Fq = q ⋅ v × B
r=
m⋅v
q⋅B
r
s = n⋅q⋅v
Massenspektrometer:
r=
m
2 ⋅ q ⋅U
⋅
q ⋅ B 1424
m3
V
Ablenkung:
Universität Kassel - Formelsammlung Physik I+II
sin α =
g⋅B
⋅L
m⋅V
10
© H.Hafke, A.Kördel, S.Rohde 2003
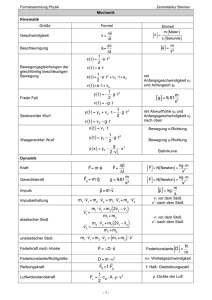
7. Impuls
7.1 Impulserhaltung:
r
dp
=F
dt
r
r
p = m⋅v
7.2 Raketenantrieb
pv = ( m + ∆mGas ) ⋅ v
pn = ∆mGas ⋅ ( v − v0 ) + m ⋅ ( v + ∆v )
m⋅
dv
dm
= −v0
dt
dt
FR = v0
dm
dt
m0
m
Raketengeschwindigkeit:
v = v0 ⋅ ln
Flugzeugantrieb:
mF ⋅ v = mF ⋅ ( v + d ⋅ v ) + d ⋅ mL ⋅ ( vQ − v0 )
mF ⋅
dm
dv
= ( v0 − v ) ⋅ L − α ⋅ v
dt
dt
⎛
⎛ t ⎞⎞
v = vE ⋅ ⎜ 1 − exp ⎜ − ⎟ ⎟
⎝ τ ⎠⎠
⎝
vE = v0 ⋅
m& L
m& L + α
⎛ vE ⎞ ⎛ mF ⎞
⎟⋅⎜
⎟
⎝ v0 ⎠ ⎝ m& L ⎠
τ =⎜
7.3 Stoßvorgänge
p2
m2v 2
=
2⋅m 2⋅m
ideal elastisch:
Ekin =
ideal inelastisch:
p12
pE 2
=
+Q
2 ⋅ m 2 ⋅(m + M )
14243
≈0
m1 − m2
⋅ p1
m1 + m2
1-dimensionaler Stoß:
P1 =
inelastischer Stoß:
P1 + P2 = 0
Universität Kassel - Formelsammlung Physik I+II
⎫
2
2 ⎪
P
P ⎬
Q= 1 + 2 ⎪
2 ⋅ m1 2 ⋅ m2 ⎭
11
P2 =
2 ⋅ m1
⋅ p1
m1 + m2
Ekin1 = Q ⋅
m2
m1 + m2
Ekin 2 = Q ⋅
m1
m1 + m2
© H.Hafke, A.Kördel, S.Rohde 2003
Kernspaltung:
Q = ∆m ⋅ c 2
Aufprall eines Pkw's:
p12
p2 2
=
+Q
2 ⋅ m 2 ⋅ ( m1 + m2 )
Q = Ekin1 ⋅
m2
m1 + m2
⎛
m2 ⎞
Ekin ? = Ekin1 − Q = Ekin ⋅ ⎜1 −
⎟
⎝ m1 + m2 ⎠
2-dimensionaler Stoß:
p12 = P 21 + P2 2 + 2 ⋅ P1 ⋅ P2 ⋅ cos γ
p12 = P12 + P2 2 ⋅
cos γ =
m1
m2
P2 ⎛ m1 − m2 ⎞
⋅⎜
⎟
2 ⋅ P1 ⎝ m2 ⎠
P12
p12 ⎛ m1 − m2 ⎞
=
⋅⎜
Restenergie der stoßenden Masse m1: E =
⎟
2 ⋅ m1 2 ⋅ m1 ⎝ m1 + m2 ⎠
Universität Kassel - Formelsammlung Physik I+II
12
2
© H.Hafke, A.Kördel, S.Rohde 2003
8. Relativitätstheorie
8.1 Lichtausbreitung / Geschwindigkeit
klassisch:
w =u+v
neue Formel:
w=
u+v
u+v
1+ 2
c
8.2 Zeitdilatation
tA =
tB
v2
1− 2
c
t A : ruhend
t B : bewegt
(1 + x) m = 1 + mx ± ... ; x  m, alle m
8.3 Relativistische Masse & Energie
Energie wird überführt in Masse:
dE = c2 ⋅ dm
Ma s s e :
m=
m0
1−
v2
c2
Energie:
E = m ⋅ c2
Ruheenergie:
E 0 = m0 ⋅ c2
Kinetische Energie:
E k = m ⋅ c2 − m0 ⋅ c2
Im elektrische Feld:
Ek = q ⋅ U = e ⋅ U
m 0 : Ruhemasse
e=_q
8.4 Raum und Zeit:
Lorenzkontraktion (bewegter Maßstab):
v2
LA = LB ⋅ 1 − 2
c
Lorenztransformation(bewegter Beobachter): x ' =
x − v⋅t
1−
Gleichzeitigkeit:
Universität Kassel - Formelsammlung Physik I+II
⎛ v⎞
⎜ 2 ⎟ − x1
c
t1' = ⎝ ⎠
v2
1− 2
c
13
v2
c2
⎛ v⎞
t −⎜ 2 ⎟⋅x
⎝c ⎠
t' =
v2
1− 2
c
⎛ v⎞
⎜ 2 ⎟ − x2
c
t '2 = ⎝ ⎠
v2
1− 2
c
© H.Hafke, A.Kördel, S.Rohde 2003
9. Schwingungen
9.1 Darstellung
y = y0 ⋅ cos(ωt − ϕ)
−
2π
⋅ ∆T = −ω⋅ ∆T = −ϕ
T
t ' = t − ∆T
y = (y0 ⋅ cos ϕ) ⋅ cos ωt + (y0 ⋅ sin ϕ) ⋅ sin ωt
14243
14243
A
B
9.2 Mechanische & elektrische Schwingungen
allgemein:
&&
x + 2 ⋅ δ ⋅ x& + ω02 ⋅ x = 0
1. mechanisch:
m ⋅ &&
y= −
D⋅ y −
R ⋅ y&
{
{
rücktreibend Reibung
1444
24443
Schwingungsgleichung für y(t)
2.elektrisch:
UC + UL + UR = 0
Q
+ L ⋅ &I{ + R ⋅ I{ = 0
C
&&
&
Q
Q
144
4
2444
3
Schwingungsgleichung für Q(t )
M *g = D * ∆z
Auto:
Variable
Dämpfung
Eigenfrequenz
allgemein
X
δ
ω0
mechanisch
Y
R
2⋅m
D
m
elektrisch
Q
R
2⋅L
1
L⋅C
Schwingungsgleichung:
x = x 0 ⋅ exp(−δ ⋅ t) ⋅ cos(ωd ⋅ t)
Frequenz:
ωd2 = ω02 − δ2 ≤ ω02
Normalfall:
δ≠0
Kriechfall:
δ > ω0
Grenzfall:
ωd = 0
Spezialfall:
ungedämpfteSchwingung
Universität Kassel - Formelsammlung Physik I+II
δ  ω0
ωd ≈ ω0
nur exp Abfall( Masse m im Honig)
δ = ω0
14
δ=0
© H.Hafke, A.Kördel, S.Rohde 2003
9.4 Erzwungene Schwingung, Resonanz
zusätzliche Kraft:
Fν = F0 ⋅ cos(Ω ⋅ t)
Schwingungsgleichung:
&&
y + 2 ⋅ δ ⋅ y& + ω02 ⋅ y = y0 ⋅ ω02 ⋅ cos(Ω ⋅ t)
Mechanischer Ansatz:
y = y r ⋅ cos(Ω ⋅ t)
1. δ = 0
2. δ ≠ 0
y r = y0 ⋅
ω02
ω02 − Ω 2
ω02
y r = y0 ⋅
(ω02 − Ω 2 ) 2 + 4 ⋅ δ 2 ⋅ Ω 2
Resonanzkurve:
y = y r ⋅ cos(Ω ⋅ t − ϕ)
Resonanzfrequenz:
ω2r = ω02 − δ 2 ≈ ω02
Maximal:
y max =
Halbwertbreite:
∆ω = δ ⋅ 3
elektrisch:
&& + 2 ⋅ δ ⋅ Q
& + ω2 ⋅ Q = Q ⋅ ω2 ⋅ cos(Ω ⋅ t)
Q
0
0
0
y0 ⋅ ω0
2⋅δ
&&
UL = L ⋅ C ⋅ U
C
UR = U0 ⋅
Universität Kassel - Formelsammlung Physik I+II
15
ω02
(ω02 − Ω 2 ) 2 + 4 ⋅ δ 2 ⋅ Ω 2
© H.Hafke, A.Kördel, S.Rohde 2003
10. Wellen
10.1 Darstellung von Wellen
y = y0 ⋅ cos(kx − ωt)
k=
2⋅π
λ
λ
c
T=
f=
c
λ
c=
ω
k
ω=
2⋅π⋅c
λ
ψ = ψ ' ⋅ cos(x − c ⋅ t)
Wellenpuls:
2⋅π
⋅ x)
λ
⎛ 2⋅π
⎞
t > 0; u = u 0 ⋅ cos ⎜
(x − ct) ⎟
⎝ λ
⎠
t = 0; u = u 0 ⋅ cos(
bei festem M:
2⋅π ⎞
⎛
u = u 0 ⋅ cos ⎜ ϕ −
ct ⎟
λ
⎝
⎠
10.2 Wellenphänomene: Schall und Licht
1. elektromagnetische Wellen:
W=
1
⋅ ε 0 ⋅ E 02
2
ε0=_ε0
C0=_c
Intensität:
s=
1
⋅ ε 0 ⋅ E 02 ⋅ c0
2
Brechzahl n in Materie:
λ=
λ0
n
transversal:
ur ur
H⊥K
2. Schallwellen:
Intensität:
3. Zusammenhang mit elektrischen
und magnetischen Größen:
c=
c0
n
ur ur
E⊥H
H=
ε0
⋅E
µ0
⎛1
⎞
W = n ⋅ ⎜ ⋅ m 0 − v02 ⎟
⎝2
⎠
⎛1
⎞
s = W ⋅ cs = ⎜ ⋅ n ⋅ m0 ⋅ u 02 ⎟ ⋅ cs
⎝2
⎠
c0 =
1
ε 0µ 0
Intensität:
1
I = c ⋅ ⋅ ε 0 ⋅ E 02
2
Longitudinale Wellen:
Schall
Energiedichte:
1
1
W = n ⋅ ⋅ m ⋅ v02 = ⋅ρ ⋅ ω2 ⋅ u 02
2
2
(Energietransport pro Zeit und Fläche)
Intensität:
Universität Kassel - Formelsammlung Physik I+II
S = W ⋅c =
1
⋅ρ ⋅ c ⋅ ω2 ⋅ u 02
2
16
© H.Hafke, A.Kördel, S.Rohde 2003
10.3 Ausbreitung von Wellen
y = y0 ⋅ cos(± kx − ωt)
Laufrichtung:
k>0 nach rechts
stehende Welle:
y = cos(kx) ⋅ cos(ωt)
r uur
rr
u = u 0 ⋅ cos(kx − ωt)
ebene Welle:
k<0 nach links
Kugelwelle:
R⎞
⎛
u = ⎜ u*0 ⋅ ⎟ ⋅ cos ( k r ⋅ r − ωt )
r⎠
⎝
Energiedichte:
⎛R⎞
E 0 = E* ⎜ ⎟
⎝r⎠
R=_rc
speziell Lichtwelle:
Energiedichte:
Intensität:
W=
S=
1
⋅ ε 0 ⋅ E 02
2
E 0 : Amplitude der Welle
1
⋅ ε0 ⋅ E 02 ⋅ c
2
10.4 Interferenz
⎛ 2⋅π ⎞
⋅x⎟
1. y1 = cos ⎜
⎝ λ
⎠
⎛ 2⋅π
⎞
2. y 2 = cos ⎜
⋅ (x + ∆x ⎟
⎝ λ
⎠
1+2 bei Überlagerung
rk − ten = k ⋅ λ 0 ⋅ R
Verstärkung für:
∆x = ± n ⋅ λ
Auslöschung für:
∆x =
Beugung am Gitter:
∆x = d ⋅ sin ϑ
Verstärkung für d ⋅ sin ϑ = n ⋅ λ
dünnes Plättchen:
∆x = 2 ⋅ h = n ⋅ λ
Verstärkung für h = n ⋅
λ
2
Verstärkung für h = n ⋅
λ
2
λ 3⋅ λ 5⋅ λ
;
;
...
2 2
2
Michelson Interferometer: ∆x = (l2 − l1 )
2 ⋅ h = (l2 − l1 )
∆x = 2 ⋅ h = n ⋅ λ
Universität Kassel - Formelsammlung Physik I+II
17
© H.Hafke, A.Kördel, S.Rohde 2003
10.5 Dopplereffekt
f0 =
c
λ
⎛ v⎞
f = f 0 ⋅ ⎜1 ± ⎟
⎝ c⎠
(+)Annäherung
(−)Wegbewegung
bewegter Empfänger sieht (c-v)
10.7 Beugung
Auflösungsgrenze:
ε≥
0, 6 ⋅ λ
; n : Brechzahl vor Objektiv
n ⋅ sin α
Näherung:
ε≥
λ
2
Numerische Apertur:
NA = n ⋅ sin α
Fernrohr:
sin λ ≈ tan λ ≈
D2
d
Öffnung :D
Abstand:d
Universität Kassel - Formelsammlung Physik I+II
18
d≤
ε ⋅ ( D 2)
0, 6 ⋅ λ
© H.Hafke, A.Kördel, S.Rohde 2003
11. Wellen und Quanten
11.1 Thermische Strahlung
KB=_k
Absorptionsvermögen:
α (λ )
„ideal schwarz“ α = 1
Emissionsvermögen:
ε (λ )
idealer Strahler ε = 1
∆s = Iλ ⋅ ∆λ; [ Iλ ] =
2 ⋅ π ⋅ c2 ⋅ h
⋅
λ5
W
m3
1
⎛ h ⋅c ⎞
exp ⎜
⎟ −1
⎝ λ ⋅ KB ⋅ T ⎠
Planck’sche Strahlung:
Iλ =
Absolute Temperatur:
T = ( 273 + Θ°C )
Wien-Verschiebungsgesetz:
λ max ⋅ T = 2,93 ⋅10−3 m ⋅ K
Energie-Quant:
E = h ⋅f =
h=_h
Kelvin, K
h ⋅c
λ
Leistungsdichte (Abstrahlung pro Fläche):
S = ε ⋅ σ ⋅ T 4 σ : Stefan Boltzmann Konstante
Abgestrahlte Leistung:
P = A ⋅S = A ⋅ ε ⋅ σ ⋅ T
ε ≤ 1: Emissionsvermögen
Schwarzer Strahler:
⎛ I1 ⎞
⎛ I1 ⎞
⎜ ⎟ =⎜ ⎟
⎝ I 2 ⎠ real ⎝ I 2 ⎠ideal
Abstrahlungsverhältnis:
⎛ T1 ⎞
⎜ ⎟ ;IR-Sensoren
⎝ T2 ⎠
Leuchtkraft von Sternen:
PS
SΘ =
4⋅π⋅3
d2
14
4244
σ =_σ
4
A : strahlende Fläche
PS
PE
=
2
4⋅π⋅d
π ⋅ R E2
4
SE = 1400
W
m2
Leuchtkraft : LΘ
empfangeneStrahlungim Abstand d
rechnerisch auf gesamte Erde bezogen: Tag/Nacht, Äquator/Pole
⇒ S'E =
1
⋅ SE
4
L
R 2 T4 d2 S
= 2 ⋅ 4 = 2 ⋅
L Θ R Θ TΘ d Θ S Θ
11.4 Lichtelektrischer Effekt
E K = (h ⋅ f − h ⋅ f 0 ) =
e ⋅ Ug
{
Spannungsgrenze
Austrittsarbeit, Auslöseenergie:
Universität Kassel - Formelsammlung Physik I+II
W0 = h ⋅ f 0
19
λ≤
h ⋅c
W0 ⋅ e
© H.Hafke, A.Kördel, S.Rohde 2003
11.5 Welle-Teilchen:
Lichtquanten, Photonen:
h=_h
E = h ⋅f
h
p=
λ
m eff ⋅ c 2 = h ⋅ f = h ⋅
m eff =
c
λ
h
λ
Energie und Impulserhaltung:
λ ' − λ = λ c (1 − cos υ)
Teilchen: Elektronen
EK =
λ c :Comton Welle = 2, 2 ⋅10−12 m
2
m2 ⋅ v2
p2
1 ⎛h⎞
=
=
⋅⎜ ⎟
2⋅m
2⋅m
2
⋅
m
⎝ λ3
⎠
1424
Materiewellede Broglie
eV → E = E ⋅ e
E
E → eV =
e
Universität Kassel - Formelsammlung Physik I+II
20
© H.Hafke, A.Kördel, S.Rohde 2003
12. Atombau
12.1 Bohr-Atommodell
2
⎛ 1 ⎞ ⎛ ε ⋅h ⎞ 2 ⎛ 1 ⎞
rn = ⎜ ⎟ ⋅ ⎜ 0
⋅ n = ⎜ ⎟ ⋅ r0 ⋅ n 2
2 ⎟
Z
π
⋅
m
⋅
e
⎝ ⎠ ⎝
⎝ Z⎠
⎠
n : Quantenzahl
h=_h
⎛ m ⋅ e4 ⎞ 1
1
E n = − Z2 ⋅ ⎜
⋅ 2 = − Z2 ⋅ E R ⋅ 2
2
2 ⎟
n
⎝ 8 ⋅ ε0 ⋅ h ⎠ n
fR =
r0 =_rb
ER
h
ER = 2,18 10-18 J = 13,6 eV
12.2 Energie-Übergänge
f = Z2 ⋅ f R ⋅
1
1
− 2
2
n
m
∆E = Z2 ⋅ E R ⋅
m → n : Emission
1
1
− 2
2
n
m
fR =
n → m : Absorption
ER
=Rydbergfrequenz
h
fr
12.3 Röntgenstrahlung
Röntgenbremsstrahlung:
EK = e ⋅ U ≥ h ⋅ f
Grenzfrequenz:
f max =
Grenzwellenlänge:
λ grenz =
Materiewellenlänge:
λ max =
Charakteristische Strahlung (K α ) :
f Kα = (Z − 1) 2 ⋅ f R ⋅
Anregung:
e ⋅ U 0 ≥ (Z − 1) 2 ⋅ E R
Universität Kassel - Formelsammlung Physik I+II
e⋅U
h
h ⋅c
e ⋅ U0
=
c
f max
λ ≥ λ grenz
e=_q
h
h
=
m⋅v p
21
3
4
© H.Hafke, A.Kördel, S.Rohde 2003
13. Physik der Gase
13.1 Temperatur und Wärmeenergie
∆
Q =
{
Energie
⋅ m ⋅ ∆T
c{
spez.Wärme
u=_mp
13.2 Atome und Moleküle
Atommasse:
mA = A ⋅ u
Massenzahl:
A=
+
Z
{
Anz.Pr otonen
Symb
Ar
H2
O
O2
N
{
Anz.Neutronen
1kmol =ˆ Akg
A = 12
C
Z=6
A
40
2
16
32
N = n ⋅ N0
N0 =
Anzahl Moleküle pro kmol:
A ⋅ kg ⋅ mol−1
= 6, 022 ⋅1026 kmol
A⋅u
Avogadrokonstante
N0=_na
13.2 Thermische Energie der Gase
Freiheitsgrade =ˆ Möglichkeit zur Energieaufnahme
E=
Energie pro Atom und pro Freiheitsgrad:
Translation
Rotation
Stoff f
H2
5
He
3
5
N2
5
O2
Ar
3
H2O 6
CO2 5
f
1-atomig
3
2-atomig,
linear
3
2
5
räumlich
3
3
6
Innere Energie:
1
⋅ KB ⋅ T
2
3
f
U = N ⋅ ⋅ KB ⋅ T
2
f
U = n ⋅ ⋅R ⋅T
2
R=_rc
KB=_k
m uuv 3
E K = ⋅ v2 = ⋅ K B ⋅ T
2
2
Gaskonstante:
R = N 0 ⋅ K B = 8,314 ⋅10−3
Maxwellverteilung:
( )
uur
v2
1
2
( )
1
2
( )
1
2
uur
w = 0,83 ⋅ v 2
≥v
( )
uur
v = 0,92 ⋅ v 2
Universität Kassel - Formelsammlung Physik I+II
J
K ⋅ kmol
22
1
2
uur
v ≈ v2
typisch 2000
m
s
© H.Hafke, A.Kördel, S.Rohde 2003
13.4 Zustandsgleichung des idealen Gases
Normaldruck:
p0 = 1, 013bar
Normaltemp:
T0 = °C = 273,15°K
Normalvolumen:
V0 =
Druck:
p=
Flüssigkeit:
p = δ ⋅ g ⋅(h − z)
Gase:
QK
= Ew
Wg
p=
R ⋅ T0
m3
= 22, 4
p0
kmol
F
A
1 Pascal = 1
N
m2
1bar = 105 Pa
N
⋅ KB ⋅ T
V
KB=_k
p ⋅ V = N ⋅ KB ⋅ T
für Anzahl der Atome
p⋅V = n ⋅R ⋅T
für Anzahl der Moleküle
R=_rc
Druck durch Gewicht ≈ 0 , Druck =ˆ Stoß der Moleküle auf Wand (Kolben)
13.5 p-V-Diagramm
p = N ⋅ KB ⋅
1
1
⋅T = n ⋅R ⋅ ⋅T
V
V
Isotherme: T=const.
Isobare:
p=const.
Isochore:
V=const.
Universität Kassel - Formelsammlung Physik I+II
23
© H.Hafke, A.Kördel, S.Rohde 2003
14. Thermodynamik
14.1 Mechanische Arbeit
W = F⋅l
isobarer Vorgang:
W = p ⋅ (V2 − V1 )
W = n ⋅ R ⋅ (T2 − T1 )
isochorer Vorgang:
W=0
isothermer Vorgang:
W12 = n ⋅ R ⋅ T ⋅ ln
Vorzeichen:
(+) Arbeit nach aussen!
V2
V1
R=_rc
(-) Arbeit von aussen!
14.2 Energieerhaltung (1.Hauptsatz)
Wärmeenergie:
Q = ∆U + W
dQ = dU + p ⋅ dV
a) Isochor:
b) Isotherm:
∆V = 0 → W = 0
W=0
⎛f
⎞
Q = ∆U = ⎜ ⋅ n ⋅ R ⎟ ⋅ ∆T
⎝2
⎠
p1 p 2
=
T1 T2
∆T = 0
p1 ⋅ V1 = p 2 ⋅ V2
∆U = 0
Q = W = n ⋅ R ⋅ T ⋅ ln
c) Isobar:
d) Abiatisch:
(thermische Isolation oder
schnelle Vorgänge)
V2
V1
⎛V ⎞
W = p1 ⋅ V1 ⋅ ln ⎜ 2 ⎟
⎝ V1 ⎠
p=const.
W = p ⋅ ∆V
⎛ f+2
⎞
Q= ⎜
⋅ n ⋅ R ⎟ ⋅ ∆T
⎝ 2
⎠
V1 V2
=
T1 T2
Q=0 x=
T2 ⎛ V1 ⎞
=⎜ ⎟
T1 ⎝ V2 ⎠
f +2
f
n⋅R
⋅ ∆T
x −1
Wges = W12 + W23
W=
p1 ⋅ V1x = p 2 ⋅ V2x
p1 ⎛ T1 ⎞ x −1
=⎜ ⎟
p 2 ⎝ T2 ⎠
x
x −1
speziell: Wärme pro kmol
f
⋅n⋅R
2
f +2
p = const. c p =
⋅n⋅R
2
v = const. c v =
Universität Kassel - Formelsammlung Physik I+II
24
© H.Hafke, A.Kördel, S.Rohde 2003
14.4 Wärmekraftmaschine
Stirlingmotor:
(1,2) , (3.4) Isotherm
Q12 = W12 = n ⋅ R ⋅ T1 ⋅ ln
V2
V1
Q34 = W34 = − n ⋅ R ⋅ T3 ⋅ ln
(2,3) , (4,1) Isochor
(+) Heizen
V2
V1
(−) Kühlen
Q 23 =
f
⋅ n ⋅ R ⋅ (T3 − T1 )
2
( −)
Q 41 =
f
⋅ n ⋅ R ⋅ (T1 − T4 )
2
(+)
R=_rc
Q 23 = −Q 41 → ideal = Umschaukeln
Tmax − Tmin
Tmax
Wg
Nutzen
= +
Aufwand Q
Wirkungsgrad:
η=
Stirling ideal:
Wg = W12 + W34
Q + = Q12
Benzinmotor:
(12)(34) Adiabatisch
(23)(41) Isochor
ηtheor
Carnot-Prozeß:
η=
⎛V ⎞
Wg
= + = 1− ⎜ 1 ⎟
Q
⎝ V2 ⎠
x −1
≈ 0, 6
(12)(34) Isotherm
η=
Wg
Q
+
= ηid =
(23)(41) Adiabatisch
Tmax − Tmin
Tmax
14.5 Kreisprozesse:
Energieerhaltung:
Q + + Q − = Wg + ∆
U
{
=0
Leistungsziffer Ew:
Wärmepumpe:
Universität Kassel - Formelsammlung Physik I+II
Qw
= Ew
Wg
25
Kältemaschine:
Qk
= Ew
Wg
© H.Hafke, A.Kördel, S.Rohde 2003
14.6 Reale Gase:
reales Gas für ein mol:
p = pid − ∆p = pid −
Vm = Vid +
d
Vm2
b{
zusätzlich wegen Moleküle
pid Vid = R T
1 kmol:
⎛
a ⎞
⎜ p + 2 ⎟ ( Vm − b ) = R T
Vm ⎠
⎝
V
Volumen Vm =
n
Sonderfall"ideal"
Van-der-Waals Gl. Für id. Gase:
a = 0; b = 0
⎛V⎞
p⎜ ⎟ = R T
⎝n⎠
Universität Kassel - Formelsammlung Physik I+II
26
© H.Hafke, A.Kördel, S.Rohde 2003
15. Ti-Konstanten
Lichtjahr
m
m
, c0 = 2,99793 ⋅108
s
s
m
cs = 331
s
1Lj = 9, 4 ⋅1015 m
Parsec
1Parsec = 3,1⋅1016 m = 3,3Lj
Elektr. Elementarladung
e = 1, 60219 ⋅10−19 A ⋅ s
Lichtgeschwindigkeit
Schallgeschwindigkeit
c = 3 ⋅108
−31
Masse Elektron
m0 = 9,11⋅10 kg
Atomare Masseneinheit
Masse Proton
Masse Neutron
Atommasse
Massenzahl
u = 1, 66 ⋅10−27 kg
Erdbeschleunigung
Energienutzung
Gravitationskonstante
Erdmasse
Permeabilität
Dielektrizitätszahl
Bohrsches Magneton
Elektronenvolt
_c
_q
_me
_mp
_mn
mA = ( Z + N ) ⋅ u
A = (Z + N )
m
g = 9,81 2
s
1t Steinkohle ≈ 29,3·109 J
1kg Kohle ≈ 3·107 J
1l Benzin ≈ 4·107 J
1kWh ≈ 3,6·106 J ≈ 0,1l Benzin
150kWh pro Person pro Tag
N ⋅ m2
G = 6, 67 ⋅10−11
kg 2
M E = 5,98 ⋅1024 kg
V ⋅s
µ0 = 4 ⋅ π ⋅10−7
A⋅ m
A⋅ s
ε 0 = 8,854 ⋅10−12
V ⋅m
−24
µ B = 9,3 ⋅10 A ⋅ m 2
1eV = 1, 6 ⋅10
−19
J
_g
_gc
_µ0
_ε0
_µb
_eV
−
Ruheenergie
e : E0 ≈ 0,5MeV
p + , n : E0 ≈ 1GeV
Wiensche-Konstante
h = 6, 63 ⋅10−34 J ⋅ s
J
k B = 1,38 ⋅10−23
K
W
σ = 5, 67 ⋅10−8 2 4
m ⋅K
−3
2,9 ⋅10 K ⋅ m
Bohr-Radius
r0 = 5,3 ⋅10−11 m
Planck-Konstante
Boltzmann-Konstante
Stephan-BoltzmannKonstante
−18
_h
_k
_σ
(greek S)
_rb
Rydberg-Energie
ER = 2,18 ⋅10
J = 13, 6eV
Rydbergfrequenz
Absoluter Nullpunkt
f R = 3, 29 ⋅1015 Hz
−273°C  0° K
Universität Kassel - Formelsammlung Physik I+II
27
© H.Hafke, A.Kördel, S.Rohde 2003
Normaldruck
Avogrado-Zahl
Gas-Konstante (innere
Energie)
Normalvolumen für
1kmol
Druck
p0 = 1,013bar
1
kmol
J
R = 8,314 ⋅103
kmol ⋅ K
R ⋅ T0
m3
= 22, 413
V0 =
p0
kmol
N
1 2 = 1 Pascal , 1bar = 105 Pascal ,
m
10 N
1bar =
cm 2
N 0 = 6, 022 ⋅1026
Universität Kassel - Formelsammlung Physik I+II
28
_na
_rc
_vm
© H.Hafke, A.Kördel, S.Rohde 2003