Abschnitt 5, 2. Übungsstunde

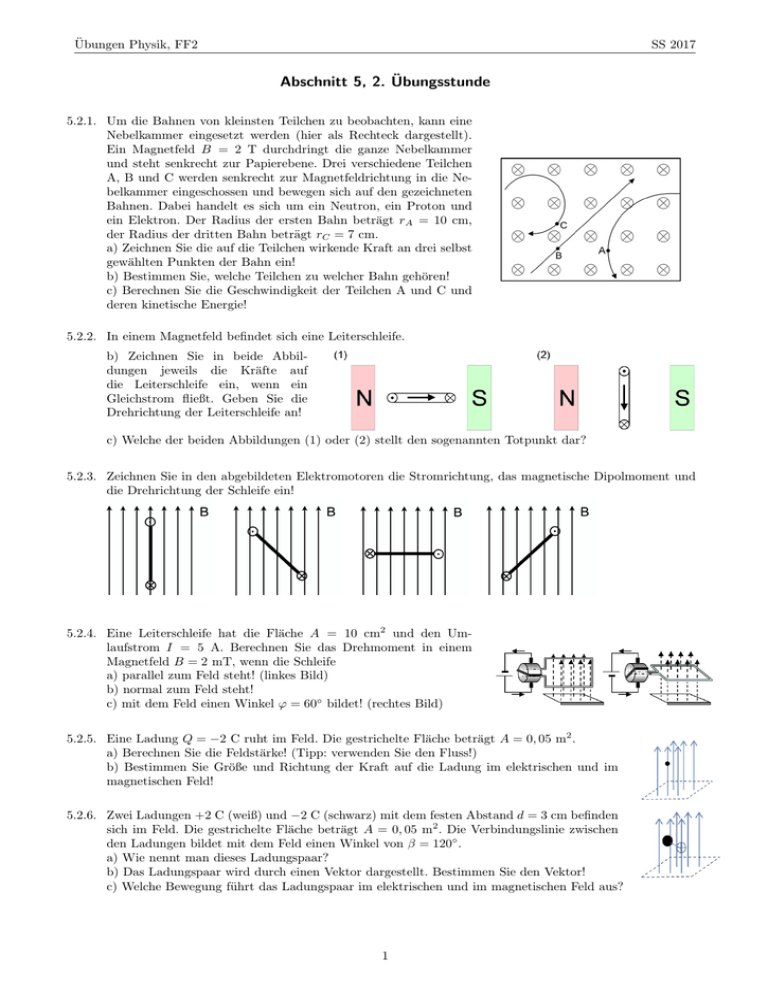
Übungen Physik, FF2
SS 2017
Abschnitt 5, 2. Übungsstunde
5.2.1. Um die Bahnen von kleinsten Teilchen zu beobachten, kann eine
Nebelkammer eingesetzt werden (hier als Rechteck dargestellt).
Ein Magnetfeld B = 2 T durchdringt die ganze Nebelkammer
und steht senkrecht zur Papierebene. Drei verschiedene Teilchen
A, B und C werden senkrecht zur Magnetfeldrichtung in die Nebelkammer eingeschossen und bewegen sich auf den gezeichneten
Bahnen. Dabei handelt es sich um ein Neutron, ein Proton und
ein Elektron. Der Radius der ersten Bahn beträgt rA = 10 cm,
der Radius der dritten Bahn beträgt rC = 7 cm.
a) Zeichnen Sie die auf die Teilchen wirkende Kraft an drei selbst
gewählten Punkten der Bahn ein!
b) Bestimmen Sie, welche Teilchen zu welcher Bahn gehören!
c) Berechnen Sie die Geschwindigkeit der Teilchen A und C und
deren kinetische Energie!
5.2.2. In einem Magnetfeld befindet sich eine Leiterschleife.
b) Zeichnen Sie in beide Abbildungen jeweils die Kräfte auf
die Leiterschleife ein, wenn ein
Gleichstrom fließt. Geben Sie die
Drehrichtung der Leiterschleife an!
c) Welche der beiden Abbildungen (1) oder (2) stellt den sogenannten Totpunkt dar?
5.2.3. Zeichnen Sie in den abgebildeten Elektromotoren die Stromrichtung, das magnetische Dipolmoment und
die Drehrichtung der Schleife ein!
5.2.4. Eine Leiterschleife hat die Fläche A = 10 cm2 und den Umlaufstrom I = 5 A. Berechnen Sie das Drehmoment in einem
Magnetfeld B = 2 mT, wenn die Schleife
a) parallel zum Feld steht! (linkes Bild)
b) normal zum Feld steht!
c) mit dem Feld einen Winkel ϕ = 60◦ bildet! (rechtes Bild)
5.2.5. Eine Ladung Q = −2 C ruht im Feld. Die gestrichelte Fläche beträgt A = 0, 05 m2 .
a) Berechnen Sie die Feldstärke! (Tipp: verwenden Sie den Fluss!)
b) Bestimmen Sie Größe und Richtung der Kraft auf die Ladung im elektrischen und im
magnetischen Feld!
5.2.6. Zwei Ladungen +2 C (weiß) und −2 C (schwarz) mit dem festen Abstand d = 3 cm befinden
sich im Feld. Die gestrichelte Fläche beträgt A = 0, 05 m2 . Die Verbindungslinie zwischen
den Ladungen bildet mit dem Feld einen Winkel von β = 120◦ .
a) Wie nennt man dieses Ladungspaar?
b) Das Ladungspaar wird durch einen Vektor dargestellt. Bestimmen Sie den Vektor!
c) Welche Bewegung führt das Ladungspaar im elektrischen und im magnetischen Feld aus?
1
Übungen Physik, FF2
SS 2017
5.2.7. Die Leiterschleife (Fläche A = 200 cm2 ) mit Umlaufstrom I = 3 A befindet sich in einem
magnetischen Feld B = 4 T. Der Winkel zwischen Fläche und Feldvektor beträgt β = 120◦ .
a) Wien nennt man diese Fläche mit einem Umlaufstrom?
b) Bestimmen Sie den Vektor, durch den diese Fläche mit Umlaufstrom dargestellt wird!
c) Welche Bewegung führt die Schleife im magnetischen Feld aus?
5.2.8. In zwei parallelen Leitern (Abstand r = 8 cm) hat der Strom dieselbe Richtung (I1 = 12 A, I2 = 3 A).
a) Zeichnen sie die Magnetfeder ein, die die beiden Ströme jeweils am Ort des anderen Stroms erzeugen.
Zeichnen sie die Lorentzkräfte ein, die auf die beiden Ströme wirken!
b) Berechnen Sie die Kraft pro Länge zwischen den Leitern!
c) In welcher Entfernung vom ersten Leiter heben sich die Magnetfelder der beiden Ströme gegenseitig
auf? Zeichnen Sie für diesen Punkt die Richtung der Magnetfelder ein!
5.2.9.
a) Wir blicken in Richtung des Stroms eines geradlinigen Leiters.
i) Wie groß ist das Magnetfeld des Leiters und welche Form hat es (Skizze)?
ii) In welche Richtung zeigt der Vektor des Magnetfeldes oberhalb des Leiters und links vom Leiter?
b) Wir blicken in eine Spule (50 cm lange, Durchmesser 1,35 cm, 1000 Windungen) hinein und der
Strom bewegt sich gegen den Uhrzeigersinn.
i) Welche Richtung hat das Magnetfeld? (Skizze)
ii) Das erzeugte Magnetfeld hat eine Größe von 0,3 mT. Wie groß ist der Strom durch die Spule?
5.2.10. In einer Spule mit 800 Windungen, einer Länge von 10 cm und einem Widerstand von 45 Ω soll ein
magnetisches Feld von 12mT erzeugt werden.
a) Skizzieren Sie das Magnetfeld!
b) Welche Spannung muss an die Spule angelegt werden?
c) Man drückt die Spule nun auf eine Länge von 5 cm zusammen. Wie groß ist jetzt das Magnetfeld?
Auszug aus der Formelsammlung:
2
C
ε0 = 8, 854 · 10−12 Nm
2,
1
4πε0
|Qe | = |Qp | = 1, 6 · 10−19 C,
B=
µ0 · I
,
2π · r
B=
2
≈ 1010 Nm
C2 ,
Vs
Vs
µ0 = 1, 256 · 10−6 Am
≈ 4π · 10−7 Am
me = 9, 1 · 10−31 kg,
mp = 1, 67 · 10−27 kg
µ0 · N · I
`
2