Intro Um dieses Kapitel zu vervollständigen, reicht es

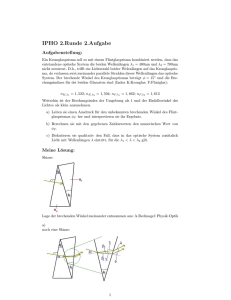
Intro
Um dieses Kapitel zu vervollständigen, reicht es also nicht, ein gerades Vorbeiführen des Fußes am Bot durchführen zu können, sondern irgendwann
möchte man ja auch mal Kurven durchfahren oder auf der Stelle wenden
können. Dazu müssen Kreisbahnen von den Füßen durchfahren werden.
Die bisher hergeleiteten Formeln für die Beinwinkel α und β gelten auch
hierfür:
p
D = b2 + r 2
b
δ = arctan
r
B 2 + D2 − C 2
β = arccos
−δ
2BD
B
γ = arcsin
· sin (β + δ) + δ
C
α = 180o − β − γ
Lediglich der Radius r (im folgenden r1 genannt) wird anders errechnet.
Genau darum soll es im folgenden gehen.
Innere Kreise
r1
τ
(ϕ + τ )
r2
κ
ϕ
Φ
r3 d
c
Man kann also an diesem Bildchen sehen, dass es schon ein bisschen kompliziert wird. Wie gesagt ist der Radius r1 der interessierende. In blau hab
ich mal beispielhaft den maximal möglichen Radius des Beins reingemalt.
1
r2
c
d
τ
...ist der Radius vom Drehpunkt des Bots; er kann frei gewählt
werden, muss aber so groß sein, dass diese Kreisbahn im „Einzugsgebiet“ des Beins liegt
...ist der Abstand in Längsrichtung des Bots der beiden Kreismittelpunkte
...der Abstand dieser Kreismittelpunkte in seitlicher Richtung
...soll wieder der Winkel sein, der vorgegeben wird
Die aufgezählten sollen jetzt die einzigen Größen sein, die vorgegeben werden. So könnte man also mit c und d den Abstand zum Schwerpunkt des
Bots angeben, wenn man um ihn drehen will.
Das etwas hervorgehobene Dreieck im Bildchen soll das Hauptaugenmerk
haben. So lässt sich etwa ganz leicht sein zweiter Schenkel r3 berechnen:
p
r 3 = c2 + d 2
Laut Tafelwerk mit seinem Kosinussatz kann man bereits die gesuchte Größe r1 folgendermaßen hinschreiben:
r12 = r22 + r32 − 2r2 r3 cos(Φ − ϕ)
Dem Sinussatz entsprechend lässt sich ϕ ausrechnen:
r2
sin κ
=
r3
sin (ϕ + τ )
r3
sin κ − τ
ϕ= arcsin
r2
Dabei sind die Winkel, wie man im Bild nach ein- oder zweimaligem Hingucken sieht:
κ= 180o − Φ − τ
c
Φ= arcsin
r2
Dabei kann das ganze auch symmetrisch betrachtet werden. Also auch negative Werte kann man für c einsetzen. Lediglich für negative d gelten diese
Gleichungen nicht mehr. Dieser Fall wird im folgenden betrachtet.
Äußerer Kreis
Für das Durchfahren einer Kreisbahn, deren Mittelpunkt außerhalb der
Grundfläche des Bots liegt muss man diese Betrachtung hier anstellen. Auch
hier hilft das Tafelwerk mit seinen Kosinussätzen weiter, sodass die erste
Form von r1 wieder hingeschrieben werden kann:
r12 = r22 + r32 − 2r2 r3 cos(Φ − ϕ)
2
Φ
ϕ
r3
d
r2
τ
r1
κ
c
Die Länge r3 ist unverändert
p
r 3 = c2 + d 2
Somit ist die einzige übrige Unbekannte der Winkel (Φ − ϕ), der bekanntermaßen irgendwas mit τ enthalten muss.
c
Φ = arcsin
r2
Der Winkel ϕ hingegen ist nicht ganz so einfach zu bestimmen. Hierfür
macht sich der Sinussatz im Tafelwerk wieder nützlich:
sin (τ − Φ)
r2
=
r3
sin κ
Das Bildchen verdeutlicht, wie sich κ zusammen setzt:
Φ
κ
τ
κ = ϕ + (90o − τ ) + 90o = 180o − τ + ϕ
3
Mit dem Sinussatz lässt sich nun also nach ϕ umstellen:
r2
sin (τ − Φ)
=
r3
sin (180o − τ + ϕ)
r3
o
180 − τ + ϕ = arcsin
sin (τ − Φ)
r2
r3
ϕ = arcsin
sin (τ − Φ) + τ − 180o
r2
Allerdings, ich vermute mal auch wieder wegen dieser Sache
(sin 45o = sin 135o ), führt dieser Winkel ϕ in die falsche Richtung, also als
würde man auch hier einen inneren Kreis betrachten (z.B. bei c = 0, τ = 0,
d = 10, r2 = 8 ergibt r1 = 18 statt der gewollten r1 = 2). Für die richtigen
Werte, genügt es einfach die −180o weg zu lassen. Es sind also in Summe
folgende Gleichungen wichtig:
c
Φ= arctan
d
r3
ϕ = arcsin
sin (τ − Φ) + τ
r2
q
r1 = r22 + r32 − 2r2 r3 cos(Φ − ϕ)
Auch hier kann das c wieder positiv und negativ sein, die Gleichungen
können auch mit dem gespiegelten Bild fertig werden.
4
Überprüfung der Ergebnisse
Da stellt sich nun also die Frage: Stimmen die Gleichungen nun jetzt überhaupt? Tolle Sache ist, dass mir eingefallen ist, wie man zeigen kann, was
die Ergebnisse überhaupt darstellen (siehe Excel-Tabelle Spalten X & Y).
Und so kann ich jetzt zeigen: ist doch nicht ganz so sehr richtig, was ich
hier ausgerechnet habe. Allerdings auch nicht falsch. Die Gleichungen sind
also richtig, nur die Gültigkeitsbereiche sind etwas anders. Fangen wir mal
mit dem „inneren Kreis“ an:
Innerer Kreis
κ = 180o − Φ − τ
c
Φ = arcsin
r2
r3
ϕ = arcsin
sin κ − τ
r2
r12 = r22 + r32 − 2r2 r3 cos(Φ − ϕ)
Gültigkeitsbereich:
Für Mittelpunkt „innerhalb“ des Bots: r2 > r3
Das liefert zum Beispiel solche Bilder:
200
150
100
50
0
-200
-150
-100
-50
0
50
Ergebnis für r2 = 150, c = 30, d = 80, (r3 = 85, 44)
5
100
150
200
Für den Mittelpunkt „außerhalb“ des Bots (also genau das, was der „äußere Kreis“ sein sollte): d > r2
Das liefert das hier:
200
150
100
50
0
-200
-150
-100
-50
0
50
100
150
200
Ergebnis für r2 = 250, c = 30, d = 300, (r3 = 301, 5)
Zu beachten wäre, dass hier das c in die negative Richtung läuft, also trotzdem es positiv mit +30 angesetzt wurde sich der Kreismittelpunkt bei −30
befindet.
Damit ist doch nun eigentlich mit einer Klappe zweifach erschlagen wollen. Steht die Frage wozu brauche ich dann noch die Gleichungen des angeblichen „äußeren Kreises“?
Äußerer Kreis
c
Φ = arctan
d
r3
ϕ = arcsin
sin (τ − Φ) + τ
r2
q
r1 = r22 + r32 − 2r2 r3 cos(Φ − ϕ)
Diese Gleichungen sind noch für einen Spezialfall zu gebrauchen, nämlich wenn der Kreismittelpunkt (um den gedreht werden soll) sich nicht
mehr „innerhalb“ des Bots befindet, also wie bei der zweiten Beschränkung der „Innerer Kreis“-Betrachtung, allerdings dessen Forderung nicht
6
erfüllt werden kann, dass d größer ist, als r2 . Somit sind diese Gleichungen
hierfür gut:
d < r2
Das liefert dann z.B. folgendes Ergebnis:
200
150
100
50
0
-200
-150
-100
-50
0
50
100
150
200
Ergebnis für r2 = 90, c = 30, d = 80, (r3 = 85, 44)
Was passiert, wenn man diese Einschränkungen verlässt, das kann jeder
für sich ausprobieren. In diesem Excel-File beinhalten die Spalten G bis K
die ersten Gleichungen (also von „Innerer Kreis“) und die übrigen Spalten
die des „Äußeren Kreises“. Hier in den Diagrammen dargestellt sind also
jeweils die Spalten X und Y.
Grüß
NRicola
7