newtonschen m s
Werbung

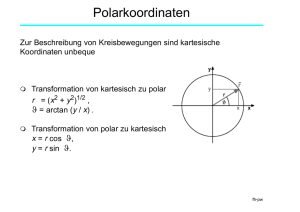
Übersicht p p p Newtonsche Gesetze Inertialsystem Ruhemasse p Übungen zur Kinematik p Übungen zur Dynamik fh-pw Newtonsche Gesetze p Erstes Axiom a = 0, wenn F = ∑ Fi = 0 i Ein Körper verbleibt beschleunigungslos (a=0, v=const.) oder in Ruhe (v=0), wenn die Resultierende der auf ihn wirkenden Kräfte null ist. p Zweites Axiom F = dP dt bzw. F = ma oder a = F m Die zeitliche Änderung des Impulses ist gleich der resultierenden Kraft, die auf den Körper wirkt - bzw.: die Beschleunigung eines Körpers ist indirekt proportional zu seiner Masse und direkt proportional zur resultierenden Kraft. p Drittes Axiom F AB = − FBA Die Kraft mit der ein wechselwirkender Körper auf einen zweiten einwirkt ist immer gleich und entgegengesetzt zu der Kraft, mit der der zweite Körper auf den ersten einwirkt („Actio = Reactio“). fh-pw Inertialsystem Alle Körper, auf die keine resultierende Kraft einwirkt, befinden sich • in Ruhe - oder - • bewegen sich mit konstanter Geschwindigkeit (Galilei, Newton 1. Axiom) Inertialsystem = ein Bezugssystem, in dem das erste Newtonsche Axiom gilt = ein Bezugssystem, das sich mit konstanter Geschwindigkeit bewegt, d.h.: es ist unbeschleunigt und rotiert nicht Beispiel: Kugel bewegt sich auf einer ebenen Fläche in einem Eisenbahnwaggon, wenn dieser sich in Bewegung setzt (Waggon ist kein Inertialsystem!) Erde ist daher (genaugenommen) kein Inertialsystem, kann jedoch in guter Näherung als Inertialsystem angesehen werden fh-pw Ruhemasse m0 Das zweite Newtonsche Axiom (F=ma) gilt nur in einem Inertialsystem F = ∑ Fi = ma i gilt nur für m = const. Relativitätstheorie → relativistische Masse : m(v ) = m0 1− v 2 c 2 Geg. : v = 10% c , c = 2,998 ⋅108 ms −1 Ges : m(v) m (v ) = m0 1 − 0,12 = m0 = 1,005 m0 0,99 m(1% c) = 1,00005 m0 Masse kann als Konstante behandelt werden fh-pw „Aufwärmübung“ Geg. : Autoreifen , R ≈ 32 cm Reifen hat nach etwa 60000 km einen Abrieb von 1 cm Ges. : durchschnittlicher Abrieb bei einer Reifenumdr ehung Abrieb 1cm 10 −2 m 1,67 ⋅ 10 −9 m = = = 6 gefahrenen Meter 60 000 km 60 ⋅10 m m 1,67 ⋅ 10 −9 m Abrieb pro Reifenumdr ehung = 2 m⋅ ≈ 3,3 ⋅ 10 −9 m m Atomradius ≈ 10 -10 m → Abrieb von etwa 33 Atomradie n (oder der Dicke eines Moleküls) fh-pw Übungen: Dimensionsanalyse Umlaufzeit eines Planeten um die Sonne: T T ist abhängig von: Radius der Umlaufbahn (r), Gravitationskonstante (G), Sonnenmasse (m) Ansatz : T ≈ r ⋅G ⋅ m a Dimension : r → L b c (Länge ), 2 r2 L G = F → MLT −2 2 m1m2 M Vergleich der Potenzen : T: 1 = −2b → b = −1 2 L: 0 = a + 3b →a= 3 2 M: 0 = −b + c → c = −1 2 m1m2 F =G 2 r m → M (Masse ), G → ... T T ≈ ( L ⋅ MLT a −2 ⋅M −2 ) ⋅M 2 b ⋅L 3 2 c 1 1 R3 ≈ r ⋅ ⋅ bzw. T ≈ G ⋅m G m R3 exakt : T = 2π G ⋅m fh-pw Übungen: Dimensionsanalyse Masse m ist am Seil mit der Länge R befestigt und rotiert mit Geschwindigkeit v auf einer Kreisbahn F R v Ansatz : F m Ges.: Dimension der Kraft, die vom Seil auf die Masse ausgeübt wird ≈ m a ⋅ vb ⋅ R c (Masse ), Dimension : m → M R→L (Länge ), , v → ... b MLT −2 L ≈ M a ⋅ ⋅ Lc T Vergleich der Potenzen : 2 v ≈ m ⋅ v 2 ⋅ R −1 = m R M: 1= a → a =1 Lösung : T: L: −2 = −b 1= b+c →b= 2 → c = −1 v2 a= Zentripetalbeschleun igung R fh-pw F Übungen: Durchschnittsbeschleunigung Porsche 911: Fahrleistung 0-100 km/h Schaltgetr. 4,2 s Ges.: durchschnittliche Beschleunigung Ges.: zurückgelegter Weg ∆v v − v0 Ansatz : a = = ∆t t − t 0 v0 = 0 m/s v = 100 a= km h 1 Ansatz : x = x0 + v0t + at 2 2 = 100 ⋅ 1000 m 3600 s x= 1 2 6,6 ms −2 ⋅ (4,2 s ) = 58,2 m 2 100 1 ⋅ ms − 2 = 6,6 ms −2 ≈ 67% g 3,6 4,2 fh-pw Übungen: Bremsweg Bei konstanter Beschleunigung gilt : a= ∆v → at = v − v0 ∆t bzw. t= v − v0 a Auto : v = 30 ms −1 Vollbremsu ng : a = −6 ms −2 Ges. : Bremsweg 1 Ausgangsgleichung : x = x0 + v0 t + at 2 2 2 v 2 − v02 v − v0 1 v − v0 x = x0 + v0 + a = x0 + a 2 a 2a v 2 − v02 ∆x = x − x0 = 2a ( v 2 − v02 0 − 30 ms −1 ∆x = = 2a 2 − 6 ms − 2 900 ∆x = m = 75 m 12 ( ) ) 2 fh-pw Übungen: „Fallschirmspringer“ ohne Schirm Fallschirm öffnet sich nicht - der Springer stürzt mit 190 km/h in einen Heuhaufen und wird dort mit konstanter Verzögerung abgebremst. Ein Mensch hält eine maximale Verzögerung von rund 40 g aus. Wie hoch muß der Heuhaufen sein, damit der Springer überleben kann? Ansatz : v 2 − v02 ∆x = (konstante Beschleunigung) 2a Ges. : ∆x Geg. : v0 = 190 km/h, v = 0 km/h, a = 40 g v 2 − v02 0-(190 km/h ) ∆x = = 2a 2 ⋅ (− 40) ⋅ 9,81 ms − 2 2 1 − 190 ms −1 3,6 = − 784,8 ms −2 2 = 3,55 m fh-pw Übungen: 1. Newtonsche Axiom Ein Helikopter bewegt sich mit einer konstanten Geschwindigkeit horizontal nach rechts. Das Gewicht des Helikopters ist 53 800 N. Die Kraft L wird durch die Rotorbewegung erzeugt und schließt einen Winkel von 21° mit der Vertikalen ein. Wie groß ist die Größe der Kraft L ? Wie groß ist die Kraft R durch den Luftwiderstand. 1.Newton : v = 0 oder v = const . wenn ∑F = 0 ∑ F = 0 → L +W + R = 0 Betrachte y - Richtung : L cos θ − W = 0 W 53800 N L= = ≈ 57600 N cos θ 0,93 Betrachte x - Richtung : L sin θ − R = 0 R = 57600 N ⋅ sin θ ≈ 20650 N fh-pw Übungen: 1. Newtonsche Axiom Java-Applet: ../mechanik1/phys/Geskraft.htm • drei Einzelkräfte auswählen • mit der Maus die Richtung und der Länge der Vektoren der Einzelkräfte (blau) anpassen • Gesamtkraft (rot) ermitteln © Walter Fendt, http://home.a-city.de/walter.fendt/phys/indexph.htm fh-pw Übungen: Reibungskräfte Geg. : Haftreibungszahl µ H zwischen Straße und Reifen sei 0,8 Ges. : Was ist der maximalen Neigungswinkel der Straße, so daß das Auto noch nicht wegrutscht? 1) Auto rutscht nicht → Summe der Kräfte = 0 2) Welche Kräfte treten auf? ∑F = F g FR Fg FN θ + FR + FN = 0 Fg θ F N FR es gilt : tanθ = FR F bzw µ H = R max = 0,8 FN FN maximaler Winkel = arctan θ = 38,7° fh-pw Java Applet: Schiefe Ebene file://.../mechanik1/Phys/schiefeebene.htm Fg m a FR θ FN Fgsinθ © Walter Fendt, 24. Februar 1999 FN= Fgcosθ θ Fg fh-pw Übungen: Haftreibung - Gleitreibung Geg. : Auto fährt mit 30 ms -1 , Reibungskoeffizienten zwischen Räder und Straße sind µ H = 0,5 und µ G = 0 ,3 Ges. : Wie weit fährt das Auto noch wenn stark abgebremst und a) die Reifen sích gerade noch drehen und b) die Räder blockieren? m 2. Newtonsche Gesetz : ∑ F = ma v x FH , FG Haft - /Gleitreibung ist proportional zur Normalkraf t FN ∑F = 0 = FN − mg ∑F = ... y x Proportionalitätsfaktor = µ H bzw. µG es gilt : FH ,max = µH FN FG = µG FN fh-pw Übungen: Haftreibung - Gleitreibung v m x FH , FG Blockierte Räder : Rollen : ∑F ∑ Fx = −µ H FN = max ax = x µ F µ mg − H N =− H = −µ H g = m m −0,5 ⋅ 9,81 ms −2 = −4,9 ms −2 ax = = −µ G FN = max µG FN µ mg =− G = −µ G g = m m −0,3 ⋅ 9,81 ms −2 = −2,94 ms −2 − Konstante Beschleunigung: Konstante Beschleunigung: ( ) 2 v 2 − v02 0- 30 ms −1 ∆x = = = 91,8 m 2a 2 − 4,9 ms −2 ( ) ( ) 2 v 2 − v02 0- 30 ms −1 ∆x = = = 153 m −2 2a 2 − 2,94 ms ( ) fh-pw Übungen: Kreisbewegung Geg. : Satellit, h = 350 km, bewegt sich mit konstanter Geschwindigkeit Ges. : Geschwindigkeit des Satelliten ( v), Umlaufzeit (T ), Beschleunigung (aS ) Ann. : Erdradius = 6350 km, Erdmasse = mE , Satellitenmasse = mS Beschleuni gung des Satelliten in 350 km Höhe Kreisbewegung daher : m m Gravitatio nsgesetz : F = G E 2 S = mS ⋅ a r m m Erdoberfläche : mS ⋅ a = G E S2 = mS ⋅ g 6350 m m Umlaufhöhe: mS ⋅ aS = G E S2 6700 v2 Zentripetalbeschleunigung a = r g mE mE 6700 =G G = 63502 67002 6350 aS 2 2 6350 2 aS = g ⋅ = g ⋅ 0.948 ≈ 0,90 ⋅ g 6700 v 2 = aS ⋅ r = 6700 km⋅ 0,90 ⋅ 9,81 ms −2 v = 7620 ms −1 Umlaufzeit : Umlaufweg 2rπ v= = Umlaufzeit T 2rπ 2 ⋅ 6700 ⋅ 3,14 km T= s= = 5524 s = 92 min −1 7620 7620 ms fh-pw Übungen: Konisches Pendel Fres = mg tan θ = ma = mg + FZ Fres θ R = L sin θ R FZ L Fres v θ FZ m mg Geg. : Masse m rotiert an einem Faden mit Länge L Ges. : Periode der Kreisbewegung mg v2 a = (Zentripetalbeschleu nigung) R 2 Rπ Länge des Umfangs v= = → T Schwingung speriode 4 R 2π 2 4π 2 a= = 2 R 2 RT T 4π 2 ma = Fres → m 2 R = mg tan θ T R L T = 2π bzw. T = 2π cosθ g tan θ g T unabhängig von m fh-pw Übungen: Verkoppelte Massen F2 a F1 Seil Seil, Masse des Seils m : Seil, Masse des Seils m = 0 : Fres = ∑ F =F1 + F2 = ma ∑ F =F + F 1 2 = 0 bzw. F1 − F2 = 0 oder F1 = F2 Zugkraft ist an beiden Enden des massenlose n Seils gleich groß fh-pw Übungen: Atwoodsche Fallmaschine F1res = m1a = Z − m1 g F2res = m2a = m2 g − Z Z a Z a m2 m1 F1 F2 Geg. : m1, m2 verbunden durch massenloses Seil Ges. : Zugkraft Z Beschleunigung a addieren : m1a + m2 a = m2 g − m1 g a= m2 − m1 g m1 + m2 (Beschleunigung) m2 − m1 g = Z − m1 g m1a = Z − m1 g → m1 m1 + m2 2m1m2 Z= g (Zugkraft) m1 + m2 fh-pw Moonjump, Bestimmung der Mondbeschleunigung p p p Bestimmung der Mondbeschleunigung Meßpunkte aus der Videosequenz Abgleich mit der theoretischen Kurve durch Wahl der Parameter y0, x0, g Das Programm Moonjump.exe können sie von der Homepage des Authors (Peter Krahmer , Universität Würzburg) laden und anschließend entpacken: http://didaktik.physik.uniwuerzburg.de/ ~pkrahmer /home/programm.html fh-pw