Aufgaben mit Lösungen zum Arbeitsblatt Stochastik II (vermischt)

R. Brinkmann http://brinkmann-du.de
Seite 1
07.06.2017
Aufgaben mit Lösungen zum Arbeitsblatt Stochastik II (vermischt)
1.
Ein Würfel wird einmal geworfen. Es werden zwei Ereignisse festgelegt.
A: Die Augenzahl ist größer als 4
B: Die Augenzahl ist eine ungerade Zahl und größer als 1
Ein neues Ereignis wird wie folgt festgelegt:
C: Die Augenzahl ist größer als 4 oder die Augenzahl ist eine ungerade Zahl
und größer als 1.
Das Ereignis C ist eine Oder – Verknüpfung aus A und B.
Bestimmen Sie die Wahrscheinlichkeit P ( C ).
(aus w_rechnung_07.doc)
E1:
P  C   P  A  B   P  A   P B   P  A  B  
2.
Eine Karte wird aus einem Spiel mit 32 Karten gezogen (Skat).
Welche Wahrscheinlichkeit hat das folgende Ereignis?
E: Die gezogene Karte ist eine Bildkarte oder eine Kreuzkarte.
1 1 1 2 2 1 3 1
      
3 3 6 6 6 6 6 2
(aus w_rechnung_07.doc)
E2:
P E   P  A  B   P  A   P B   P  A  B  
3.
Ein Fahrradschloss (Zahlenschloss) besteht aus vier unabhängig voneinander
beweglichen Rädern, die jeweils 6 Ziffern ( von 1 bis 6 )
enthalten. Das Schloss öffnet sich nur bei einer ganz bestimmten
Zahlenkombination.
Wie viele Stellungen (Zahlenkombinationen) hat das Fahrradschloss und wie
groß ist die Wahrscheinlichkeit, bei der ersten Einstellung das Schloss zu
öffnen?
12 8
3 17



 0,53125
32 32 32 32
(aus w_rechnung_09.doc)
E3: Anzahl der Zahlenkonbinationen: nk  6 4  1296
1
Die Wahrscheinlichkeit mit einem Versuch:
 0,00077
1296
4.
Aus den 26 Buchstaben des Alphabets werden nacheinander blind drei
Buchstaben mit Zurücklegen entnommen. Wie groß ist die Wahrscheinlichkeit
dreimal denselben Buchstaben zu ziehen?
(aus w_rechnung_09.doc)
E4:
Wahrscheinlichkeit, drei gleiche Buchstaben zu ziehen:
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
26
 0,00148
17576
Seite 1 von 13
R. Brinkmann http://brinkmann-du.de
5.
Seite 2
07.06.2017
In einer Lostrommel befinden sich 6 Lose mit den Nummern 1 bis 6.
Ein Spieler zieht nacheinander drei Lose. Zieht er in der Reihenfolge
die Nummern 2, 4 und 6, so hat er gewonnen.
Berechnen Sie die Wahrscheinlichkeit für einen Gewinn.
(aus w_rechnung_09.doc)
E5:
Gewinnwahrscheinlichkeit: P  A  
6.
Aus einem Kartenspiel mit 32 Karten werden 8 Karten gezogen.
Wie groß ist die Wahrscheinlichkeit dafür, dass dies 8 Karo – Karten sind?
1
 0,0083
120
(aus w_rechnung_09.doc)
E6: Die Wahrscheinlichkeit bei 8 Zügen Karo zu ziehen ist etwa 0,000 000 095
7.
Jedes Los gewinnt !
Bei der Abi - Abschlussfeier muss jeder der 50 Teilnehmer ein Los kaufen.
Der 1. Preis hat einen Wert von 100€, der 2. von 25€ und der 3. von 10€.
Jeder, der keinen dieser Gewinne bekommt, erhält einen Trostpreis in Höhe
von 1€. Wie teuer müsste ein Los sein, damit Einnahmen und Ausgaben
überein stimmen? Jedes Los wird für 5€ verkauft. Der Erlös geht ans
Friedensdorf. Wie groß ist der Erlös?
(aus w_rechnung_10.doc )
E7: Jedes Los muss 3,65 € kosten, damit die Ausgaben gedeckt werden.
Bei einem Lospreis von 5 € beträgt der Gewinn 68 €.
8. Eine Urne enthält eine rote, eine schwarze und eine grüne Kugel.
Es wird solange ohne zurücklegen eine Kugel gezogen, bis eine grüne Kugel
erscheint.
Wird die grüne Kugel im 1. Zug gezogen, so ist die Ausspielung 2€.
Wird die grüne Kugel im 2. Zug gezogen, so ist die Ausspielung 1€.
Wird die grüne Kugel im 3. Zug gezogen, so ist die Ausspielung 0€
Wie hoch muss der Einsatz sein, damit es sich um ein faires Spiel handelt?
(aus w_rechnung_10.doc )
E8: Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz 1 € betragen.
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 2 von 13
R. Brinkmann http://brinkmann-du.de
Seite 3
07.06.2017
9. Eine Münze wird 5 mal geworfen und p sei 0,5.
a) Bestimmen Sie die Wahrscheinlichkeitsverteilung der
Zufallsvariablen X: Anzahl der Wappen.
b) Mit welcher Wahrscheinlichkeit wirft man
(1) Höchstens 3 mal Wappen
(2) Weniger als 3 mal Wappen
(3) mindestens 1 mal Wappen
(4) mehr als einmal Wappen?
(aus w_rechnung_11.doc)
E9:
a)
k
0
1
2
3
4
5
1
5 10 10 5
1
PX  k
32 32 32 32 32 32
b) (1) Höchstens 3 mal Wappen
26
P  X  3 
 0,8125
32
(2) Weniger als 3 mal Wappen
16
P  X  3 
 0,5
32
(3) Mindestens 1 mal Wappen
31
P  X  1 
 0,96875
32
(4) Mehr als einmal Wappen
26
P  X  1 
 0,8125
32
10. Ein Multiple – Choice – Test besteht aus 50 Aufgaben mit jeweils 5 Antworten, von
denen nur jeweils eine richtig ist. Mit welcher Wahrscheinlichkeit kann man durch
bloßes Raten folgende Anzahl von Aufgaben richtig beantworten?
a) Mehr als 20 Aufgaben
b) Mindestens 10 und höchstens 20 Aufgaben
c) Weniger als 10 Aufgaben d) Genau 15 Aufgaben
Die Trefferwahrscheinlichkeit pro Aufgabe ist 1/5 = 0,2. Da diese Wahrscheinlichkeit
bei jeder der 50 Aufgaben besteht, kann der Vorgang als 50 stufiger Bernoulli
Versuch betrachtet werden.
Der Auszug aus der kumulierten Binomialverteilung mit n = 50 und p = 0,2 soll als
Hilfestellung genutzt werden.
k PX  k k PX  k k PX  k k P X  k k P X  k
9
10
0, 444
0,584
11
14
0,711
0,939
15
16
0,969
0,986
19
20
0,999
1,000
(aus w_rechnung_11.doc)
E10:
a) Mehr als 20 Aufgaben
P  X  21  0
b) Mindestens 10 höchstens 20
P 10  k  20   0,556
c) Weniger als 10 Aufgaben
P  X  9   0,444
d) Genau 15 Aufgaben
Erstellt von R. Brinkmann 841118780
P  X  15  0,03
19.02.2007 19:25:00
Seite 3 von 13
21
22
1,000
1,000
R. Brinkmann http://brinkmann-du.de
Seite 4
07.06.2017
11. Gegeben ist ein n- stufiger Bernoulli- Versuch mit n = 500 und p = 0,33.
Zu bestimmen ist die Wahrscheinlichkeit für die Anzahl der Erfolge im
Intervall [ 150 ; 180]. Es soll mit einer Genauigkeit von drei Stellen hinter dem
Komma gerechnet werden.
(aus w_rechnung_12.doc 1.)
E11: Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 150 ; 180 ]
beträgt etwa 85,8%
12. Bestimmen Sie die 90% - Umgebung vom Erwartungswert
für n = 550 und p = 0,36
(aus w_rechnung_12.doc 2.)
E12: Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 180 ; 216 ]
beträgt etwa 90%
13. Gegeben ist ein n- stufiger Bernoulli- Versuch. Gesucht ist die
Wahrscheinlichkeit für die Ergebnisse außerhalb von Umgebungen um den
Erwartungswert.
a) n  300 p  0,56 bestimmen Sie P  X  162
b) n  240 p  1/ 3 bestimmen Sie P  X  80
(aus w_rechnung_12.doc 3.
E13:
a) Die Wahrscheinlichkeit für weniger als 162 Erfolge ist etwa 22,4%
b) Die Wahrscheinlichkeit für mehr als 80 Erfolge ist etwa 47,2%
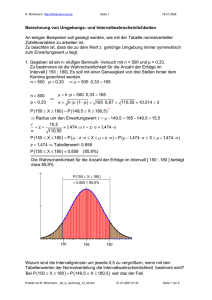
14. Bestimmen Sie die Wahrscheinlichkeit einer nicht symmetrischen Umgebung
vom Erwartungswert. n = 180, p = 0,55, Intervall: [ 89 ... 104 ].
(aus w_rechnung_12.doc 4.)
E14: Die Wahrscheinlichkeit der Erfolge im Intervall [89 ; 104] ist etwa 73,6%
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 4 von 13
R. Brinkmann http://brinkmann-du.de
Seite 5
07.06.2017
Ausführliche Lösungen:
A1: Zuerst bilden wir die Ergebnismengen von A und B.
A  5;6 B  3;5
Nach der Summenregel ist nun P  C   P  A  B   P  A   P B   P  A  B 
zu berechnen.
Dazu benötigen wir noch die Ergebnismenge von A  B.
A  B  5
Die Wahrscheinlichkeiten der einzelnen Ereignisse sind:
1 1 2 1
1 1 2 1
1
PA    
P B     
P A  B 
6 6 6 3
6 6 6 3
6
Damit wird die Wahrscheinlichkeit von C:
1 1 1 2 2 1 3 1
P  C   P  A  B   P  A   P B   P  A  B         
3 3 6 6 6 6 6 2
(aus w_rechnung_07.doc)
A2: Das Ereignis E ist eine Oder- Verknüpfung aus den Ereignissen
A: Die gesuchte Karte ist eine Bildkarte
B: Die gesuchte Karte ist eine Kreuzkarte
Zuerst bestimmen wir die Anzahl der möglichen Ergebnisse von A und B.
A: Es gibt 12 Bildkarten von insgesamt 32 Karten.
B: Es gibt 8 Kreuzkarten von insgesamt 32 Karten.
Nach der Summenregel ist nun P E   P  A  B   P  A   P B   P  A  B 
zu berechnen.
Dazu benötigen wir noch die Anzahl der möglichen Ergebnisse von A  B.
A  B : Es gibt 3 Kreuz - Bildkarten (Bube, Dame, König)
Die Wahrscheinlichkeiten der einzelnen Ereignisse sind:
12
8
3
PA 
P B  
P  A  B 
32
32
32
Damit wird die Wahrscheinlichkeit von E:
12 8
3 17
P  E   P  A  B   P  A   P B   P  A  B  



 0,53125
32 32 32 32
Die Wahrscheinlichkeit dafür, dass die gezogene Karte eine Bild- oder eine
Kreuzkarte ist beträgt etwa 0,53.
(aus w_rechnung_07.doc)
A3: Modellierung mit dem Urnenmodell:
Eine Urne enthält n = 6 Kugeln mit den Nummern 1 bis 6.
Es wird k = 4 mal gezogen mit Zurücklegen.
Die Anzahl der Zahlenkonbinationen beträgt: nk  64  1296
Die Wahrscheinlichkeit mit einem Versuch
1
die richtige Kombination zu finden ist
 0,00077
1296
(aus w_rechnung_09.doc)
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 5 von 13
R. Brinkmann http://brinkmann-du.de
Seite 6
07.06.2017
A4: Modellierung mit dem Urnenmodell:
Eine Urne enthält n = 26 Kugeln mit den Buchstaben A bis Z.
Es wird k = 3 mal gezogen mit Zurücklegen.
Die Anzahl der Buchstabenkonbinationen beträgt: nk  263  17576
Die Wahrscheinlichkeit bei drei Ziehungen z. B. 3 mal den Buchstaben A
1
zu ziehen ist
17576
3 mal B, bzw. C oder irgend einen anderen Buchstaben zu ziehen
hat jeweils die gleiche Wahrscheinlichkeit.
Es gibt mit den 26 Buchstaben des Alphabets insgesamt 26 günstige Fälle.
Damit ist die Wahrscheinlichkeit, drei gleiche Buchstaben zu ziehen:
26
 0,00148
17576
(aus w_rechnung_09.doc)
A5: Zuerst wird die Anzahl der Möglichkeiten berechnet, von diesen gibt es nur
eine, die zum Gewinn führt, nämlich die Zahlenfolge 2, 4, 6.
Es handelt sich um eine geordnete Stichprobe ohne Zurücklegen.
Aus n = 6 Zahlen werden k = 3 Zahlen gezogen.
n!
6! 6  5  4  3  2  1
Anzahl der Möglichkeiten:


 6  5  4  120
3  2 1
n  k  ! 3!
Gewinnwahrscheinlichkeit: P  A  
1
 0,0083
120
(aus w_rechnung_09.doc)
A6: Die Wahrscheinlichkeit bei 8 Zügen jeweils Karo zu ziehen ist:
n  32;k  8  Anzahl der Möglichkeiten:
n
n!
32!
32  31 30  29  28  27  26  25


 10.518.300
 
8  7  6  5  4  3  2 1
 k  k!  n  k  ! 8! 24!
1
PA 
 0,000000095  9,5  10 8
10.518.300
(aus w_rechnung_09.doc)
A7: Der Erwartungswert wird berechnet:
xi
E(X) = 3,64 bedeutet, dass jedes
Los 3,65€ kosten muss,
damit die Ausgaben gedeckt
werden.
100
Bei einem Lospreis von 5 €
und 50 verkauften Losen
entsteht ein Gewinn von
50   5  3,64  68 €
Dieser Betrag geht ans
Friedensdorf.
10
25
1
P  X  xi 
xi  P  X  xi 
1
50
1
50
1
50
47
50
100
50
25
50
10
50
47
50
182
 3,64
50
Erwartungswert E  X 
(aus w_rechnung_10.doc )
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 6 von 13
R. Brinkmann http://brinkmann-du.de
Seite 7
07.06.2017
A8:
Mit Hilfe des dreistufigen Baumdiagramms und der Pfadregel errechnet man die
Wahrscheinlichkeiten dafür eine grüne Kugel zu ziehen.
1
Ausspielung
1/2
Zug Ergebnisse
P
X
1
1/2
1/3
1
2€
 g
3
1
1/2
1 1 1
1/3
2
 
1€
 sg ; rg
6 6 3
1/2
1 1 1
3
0€
 srg ; rsg  
1/3
6 6 3
2. Zug
1. Zug
E  X  2 
3. Zug
1
1
1
 1  0   1
3
3
3
Der Erwartungswert der Ausspielung ist E(X) = 1.
Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz 1 € betragen.
(aus w_rechnung_10.doc )
A9 Das Problem kann als 5 – stufiger Bernoulli– Versuch betrachtet werden
a) mit n = 5 und p = 0,5. Gesucht ist P(X = k) für k = 0, 1, 2, 3, 4, 5
k PX  k
0
5  1   1 
0     
0  2   2 
1
1
5  1 
  
 1  2 
5  1 
2   
 2  2 
2
5  1 
3   
3  2 
3
 1
 
2
5 0
5 1
 1
 
2
52
 1
 
2
5 3
4
5  1  1
4     
4  2   2 
5  1 
5   
5  2 
5
5
1
1
 1
 1 1    5 
 0,03125
32
2
2
 1
 
2
4
5  1  1
1
5
 1
    5   5 5 
 0,15625
1 2 2
32
2
2

54  1

2  1  2 

543  1

3  2  1  2 

5432  1  1
1
5
 1
     5   5 5 
 0,15625
4  3  2 1  2   2 
32
2
2

5  4  3  2 1  1 

5  4  3  2  1  2 
54
2
3
5
1 10
 1
 1
    10     10  5 
 0,3125
32
2
2
2
3
2
5
1 10
 1
 1
    10     10  5 
 0,3125
32
2
2
2
4
5 5
Erstellt von R. Brinkmann 841118780
5

1
5
5
0
5
1
1
 1
 1
    1    1  1 5 
 0,03125
32
2
2
2
19.02.2007 19:25:00
Seite 7 von 13
R. Brinkmann http://brinkmann-du.de
Seite 8
07.06.2017
A9 (1) Höchstens 3 mal Wappen bedeutet:
b)
1
5 10 10 26
P  X  3 




 0,8125
32 32 32 32 32
(2) Weniger als 3 mal Wappen bedeutet:
1
5 10 16
P  X  3 



 0,5
32 32 32 32
(3) Mindestens 1 mal Wappen bedeutet:
5 10 10 5
1 31
P  X  1 





 0,96875
32 32 32 32 32 32
(4) Mehr als 1 mal Wappen bedeutet:
10 10 5
1 26
P  X  1 




 0,8125
32 32 32 32 32
(aus w_rechnung_11.doc)
A10: a) P  X  21  P  X  50   P  X  20   1  1  0
Die Wahrscheinlichkeit durch bloßes Raten mehr als 20 Aufgaben
richtig zu beantworten ist kleiner als 0,001 (0,1%).
b) P 10  k  20   P  X  20   P  X  9   1 0,444  0,556
Die Wahrscheinlichkeit durch bloßes Raten mindestens 10 und
höchstens 20 Aufgaben richtig zu beantworten ist 0,556 (55,6%).
c) P  X  9   0,444 direkt aus der Tabelle ablesbar.
Die Wahrscheinlichkeit durch bloßes Raten weniger als 10 Aufgaben
richtig zu beantworten ist 0,444 (44,4%).
d) P  X  15   P  X  15   P  X  14   0,969  0,939  0,03
Die Wahrscheinlichkeit durch bloßes Raten genau 15 Aufgaben richtig
zu beantworten ist 0,03 (3%).
(aus w_rechnung_11.doc)
A11:
  n  p  500  0,33  165
n  500

p  0,33
  n  p  1  p   165  0,67  110,55  10,514  3
 ... 150...165...180 ... Intervall ist symmetrisch zum Erwartungswert
P 150  X  180   P 149,5  X  180,5 
*)
 Radius um den Erwartungswert: r    149,5  165  149,5  15,5
r
15,5
z
 1, 474  r  z    1, 474  

110,55
P 150  X  180   P    z    X    z     P    1, 474    X    1, 474   
z  1, 474  Tabellenwert: 0,858
P 150  X  180   0,858
85,8% 
Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 150 ; 180 ] beträgt
etwa 85,8%
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 8 von 13
R. Brinkmann http://brinkmann-du.de
Seite 9
07.06.2017
P 150  X  180 
 0,855
150
85,5%
165
180
A12:
  n  p  550  0,36  198
n  550

p  0,36
  n  p  1  p   198  0,64  126,72  11,257  3
P    z    X    z     0,90
Der dazugehörige z- Wert wird aus der Tabelle abgelesen für P  0,90
z  1,64  Umgebungsradius: r  z    1,64  126,72  18,46
  z    198  18,46  179,54  180
  z    198  18,46  216,46  216
Das Intervall soll symmetrisch zum Erwartungswert   198 liegen.
Wir wählen: P 180  X  216 
Es ist zu prüfen, ob das Intervall  180...198...216  der Forderung (90%) entspricht.
P 180  X  216   P 179,5  X  216,5 
r
18,5
r  18,5  
 r  1,64    z  1,64
 11,257
P 180  X  216   0,899
Die Wahrscheinlichkeit für die Anzahl der Erfolge im Intervall [ 180 ; 216 ] beträgt
etwa 90%
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 9 von 13
R. Brinkmann http://brinkmann-du.de
Seite 10
07.06.2017
90%
179,5
180
190
216 216,5
A13a:
n  300
p  0,56

  n  p  300  0,56  168
  n  p  1  p   168  0,44  73,92  8,598  3
Zu bestimmen ist die Wahrscheinlichkeit für das Intervall [0 ; 161].
Aus der Tabelle kann nur die Wahrscheinlichkeit für ein um den Erwartungswert
symmetrisches Intervall abgelesen werden, dieses enthält die Werte
[162 .... 168 ... 174 ]. Daran anschließend folgt das
Intervall [175 .... 300], welches aus Symmetriegründen die gleiche Größe wie
[0 ; 161] hat. Es gilt folgender Ansatz:
[ { 0 ... 161 } {162 ... 168 ... 174 } { 175 ... 300}]
1
P  X  162   P  X  161  1  P 161,5  X  174,5  
2
r
6,5
Radius : r  168  161,5  6,5   z 
 0,756  r  0,756  

73,92
mit z  0,76 wird
P 161,5  X  174,5   P    z    X    z     0,553
und damit wird
1
1
P  X  162   1  0,553    0, 447  0,2235
2
2
Die Wahrscheinlichkeit für weniger als 162 Erfolge ist etwa 22,4%
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 10 von 13
R. Brinkmann http://brinkmann-du.de
Seite 11
07.06.2017
P  X  162   0,224  22,4%
162
A13b:
1
  n  p  240   80
n  240
3

1
p
2
160
  n  p  1  p   80  
 7,303  3
3
3
3
 0 ... 79 79,5 ... 80 ... 80,5  81 ... 240 
1
P  X  80   1  P  79,5  X  80,5  
2
r
0,5
Radius : r  80  79,5  0,5   z 
 0,068  r  0,07  

160
3
mit z  0,07 wird
P  79,5  X  80, 5   P    z    X    z     0,056
und damit wird
P  X  80   0,5  1  0,056   0,5  0,944  0, 472
Die Wahrscheinlichkeit für mehr als 80 Erfolge ist etwa 47,2%
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 11 von 13
R. Brinkmann http://brinkmann-du.de
Seite 12
07.06.2017
P  X  80   0,472  47,2%
81
A14:
  n  p  180  0,55  99
n  180

p  0,55
  n  p  1  p   99  0, 45  44,55  6,675  3
bestimmen Sie P  89  X  104 
  89...93  94...99...104  105 ...109 
Ansatz: P  89  X  104   P  89  X  93   P  94  X  104 
1
P  89  X  109   P  94  X  104  
2
1
P  89  X  104   P  89  X  109   P  94  X  104    P  94  X  104 
2
1
 P  89  X  109   P  94  X  104  
2
P  89  X  109   P  88,5  X  109,5 
P  89  X  93  
r  10,5 
r
10,5
z
 1,57  r  1,57  

6,675
P  89  X  109   0,884
P  94  X  104   P  93,5  X  104,5 
r
5,5
z
 0,82  r  0,82  

6,675
P  94  X  104   0,588
r  5,5 
1
0,884  0,588   0,736
2
Die Wahrscheinlichkeit der Erfolge im Intervall [89 ; 104] ist etwa 73,6%
P  89  X  104  
Erstellt von R. Brinkmann 841118780
19.02.2007 19:25:00
Seite 12 von 13
R. Brinkmann http://brinkmann-du.de
Seite 13
07.06.2017
P  89  X  104   0,736  73,6%
89
Erstellt von R. Brinkmann 841118780
99
104
19.02.2007 19:25:00
Seite 13 von 13