Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1

Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
S. 1/8
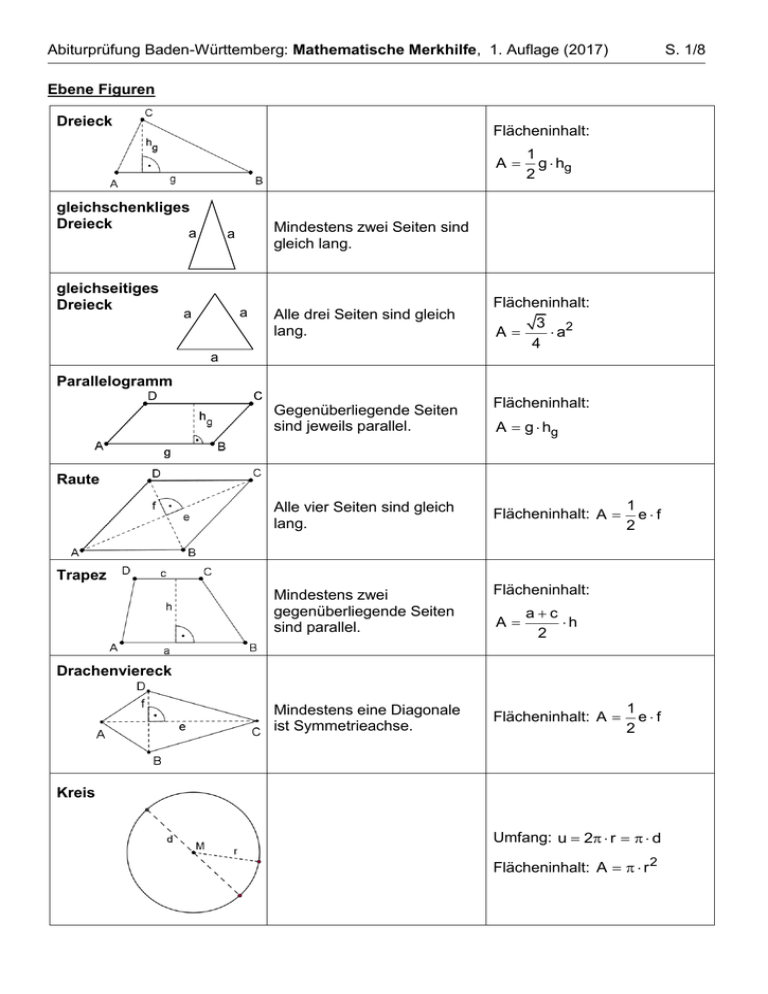
Ebene Figuren
Dreieck
Flächeninhalt:
A
gleichschenkliges
Dreieck
a
gleichseitiges
Dreieck
Mindestens zwei Seiten sind
gleich lang.
a
a
a
1
g  hg
2
Alle drei Seiten sind gleich
lang.
Flächeninhalt:
3 2
A
a
4
a
Parallelogramm
Gegenüberliegende Seiten
sind jeweils parallel.
Flächeninhalt:
Alle vier Seiten sind gleich
lang.
Flächeninhalt: A 
Mindestens zwei
gegenüberliegende Seiten
sind parallel.
Flächeninhalt:
Mindestens eine Diagonale
ist Symmetrieachse.
Flächeninhalt: A 
A  g  hg
Raute
1
ef
2
Trapez
A
ac
h
2
Drachenviereck
1
ef
2
Kreis
Umfang: u  2  r    d
Flächeninhalt: A    r 2
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
S. 2/8
Körperberechnungen
Prisma
Volumen: V  G  h
Zylinder
Volumen: V  G  h    r 2  h
Flächeninhalt der Mantelfläche: M  2  r  h
Quader
Volumen: V  a  b  c
Länge der Raumdiagonalen: e  a2  b2  c 2
Pyramide
Volumen: V 
1
Gh
3
Volumen: V 
1
  r2  h
3
Kegel
Flächeninhalt der Mantelfläche: M    r  s
Kugel
Volumen: V 
4
  r3
3
Oberflächeninhalt: O  4  r 2
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
g
Elementargeometrie
S. 3/8
h
b
Strahlensätze
ab c d

a
c
a c
 ;
b d
Falls g || h, gilt:
v
a
ab v

a
u
u
c
d
Winkelsummensatz
Die Summe der Innenwinkel im Dreieck beträgt 180°.
Satz des Thales
Liegt C auf dem Halbkreis über AB,
so ist der Winkel bei C ein rechter Winkel.
Rechtwinkliges Dreieck
Satz des Pythagoras a2  b2  c 2
Trigonometrie
sin  
a
b
a
, cos   , tan  
c
c
b
tan  
sin 
, (sin )2  (cos )2  1
cos 
Winkelfunktionen
sin
Gradmaß 
0
Bogenmaß x
0
sin
0
cos
1
30
45
60
90
1

6
1
2
1
3
2
1

4
1
2
2
1
2
2
1

3
1
3
2
1
2
1

2
1
cos
0
Potenzen und Logarithmen
Potenzen
0
x 1
x
xa  xb  xab
xa
a
a
a
x  y  (x y)
Logarithmen
a
loga (b) 
ln(b)
ln(a)
xb
xa

 1
 
x n   n x
1
xa
 x a b
 xa 
b
 xab
a
x
 
ya  y 
loga (1)  0
loga (bx )  x  loga (b)
 1
loga     loga (b)
b
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
S. 4/8
Terme und Gleichungen
 a  b 2
Binomische Formeln
Quadratische Gleichung
Potenzgleichungen
 a2  2ab  b2
2
x px  q  0
p
p
x1;2       q
2
2
a x2  b x  c  0
x1;2 
xn  a (a > 0)
falls n gerade:
x1;2   n a
falls n ungerade:
x na
falls n ungerade:
x   n a
2
x n  a (a < 0)
Exponentialgleichungen
 a  b  a  b  a2  b2
b  b2  4ac
2a
ax  b  x  loga (b) ( a,b  0 )
Geraden in der Ebene
y  mx  c
y  yP
m Q
xQ  xP
Hauptform
Steigung
Punktsteigungsform
y  m  (x  xQ )  yQ
Parallele zur y-Achse
x u
Steigungswinkel 
m  tan 
Orthogonalität
mg  mh  1  g  h
Ableitungen
f(x)
f'(x)
g(x)  h(x)
g'(x)  h'(x)
Faktorregel
c  g(x)
c  g'(x)
Potenzregel
xr
r  xr 1
Produktregel
u(x)  v(x)
u'(x)  v(x)  u(x)  v '(x)
u(v(x))
u'(v(x))  v '(x)
Ableitungsregel
Summenregel
Kettenregel
Spezielle Ableitungen
 x
'

1
2 x
'
1
 1
x  2
 
x
 sin x  '  cos x
 cos x  '   sin x
 ex 
'
 ex
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
Untersuchung von Funktionen und Graphen
Symmetrie
Spiegelung
Achsensymmetrie zur y-Achse

f (x)  f(x)
Punktsymmetrie zum Ursprung

f (x)   f(x) für alle x
an der x-Achse:
y   f(x)
an der y-Achse:
y  f(x)
Verschiebung um c in x-Richtung:
y  f ( x  c)
um d in y-Richtung:
y  f (x)  d
Streckung
Monotonie
Hochpunkt
oder
Tiefpunkt
oder
Wendepunkt
oder
für alle x
1
in x-Richtung:
b
y  f b  x 
mit Faktor a in y-Richtung:
y  a  f (x)
f '(x)  0 für alle x I 
f streng monoton wachsend auf I
f '(x)  0 für alle x I 
f streng monoton fallend auf I
mit Faktor
H( x0 | f(x0 )) , falls
f '(x0 )  0 und
Vorzeichenwechsel "+ nach –" von f ' bei x0
f '(x0 )  0 und
f ''(x0 )  0
T( x0 | f(x0 )) , falls
f '(x0 )  0 und
Vorzeichenwechsel "– nach +" von f ' bei x0
f '(x0 )  0 und
f ''(x0 )  0
W ( x0 | f(x0 )) , falls
f ''(x0 )  0 und
Vorzeichenwechsel von f '' bei x0
f ''(x0 )  0 und
f '''(x0 )  0
Tangente
Steigung mt  f '(u)
Normale
Steigung mn 
1
f '(u)
y  f '(u)(x  u)  f(u)
y
1
(x  u)  f(u)
f '(u)
allgemeine Sinusfunktion
f(x)  a  sin  b(x  c)  d
(Amplitude
|a| , Periode
2
)
b
S. 5/8
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
Integralrechnung
x
Integralfunktion
Ia (x)   f(u) du
a
Hauptsatz
Ia '(x)  f(x)
b
b
 f(x) dx  F(x)  F(b)  F(a)
a
a
t
Bestandsfunktion
F(t)  F(t0 )   f(x) dx
t0
b
Mittelwert
1
m
f(x) dx
ba
a
Volumen eines
Rotationskörpers
b
V      f(x)  dx
2
a
Stammfunktionen
Regel
Funktion
Stammfunktion
Summenregel
f(x)  g(x)
F(x)  G(x)
k  f(x)
k  F(x)
Lineare Verkettung
f a  x  b
Spezialfälle
x r (r  1)
1
 F a  x  b
a
1
 xr 1
r 1
Faktorregel
1
(x  0)
x
ln(x)
sin x
 cos x
cos x
sin x
ex
ex
Differenzialgleichung
Funktionsterm
Wachstumsfunktionen
linear
f '(t)  k
f(t)  k  t  c
exponentiell
f '(t)  k  f(t)
f(t)  a  ekt
beschränkt
f '(t)  k   S  f(t)
f(t)  S  a  ekt
S. 6/8
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
S. 7/8
Analytische Geometrie
Mittelpunkt der
Strecke AB
 a  b a  b2 a3  b3 
M 1 1| 2
|
2
2 
 2
Betrag eines Vektors
| a | a12  a22  a32
Einheitsvektor
a0 
Skalarprodukt
a  b  a1 b1  a2 b2  a3 b3
1
a
|a|
a  b  | a |  | b |  cos 
Winkel zwischen
zwei Vektoren
cos  
Orthogonalität
a  b  ab  0
Geradengleichung
g: x  p  r  u
Ebenengleichungen
Parameterform
E: x  p  r  u  s  v

ab
|a||b|

Normalenform
E: x  p  n  0
Koordinatenform
E: a x1  b x2  c x3  d
Schnittwinkel
Gerade – Gerade
Gerade – Ebene
Ebene – Ebene
cos  
| u1  u2 |
| u1 |  | u2 |
|un|
|u|| n|
| n1  n2 |
cos  
| n1 |  | n2 |
sin  
Abstandsberechnungen
AB  (b1  a1)2  (b2  a2 )2  (b3  a3 )2
Punkt – Punkt
d(A;B) 
Punkt – Ebene
HNF von E:  x  p   n0  0 bzw.


d(Q;E)  q  p  n0
Windschiefe Geraden
bzw.
a x1  b x2  c x3  d
0
a2  b2  c 2
d(Q;E) 
a q1  b q2  c q3  d
g: x  p  r  u ; h: x  q  s  v


d(g;h)  q  p  n0 , wobei n0  u und n0  v
a2  b 2  c 2
Abiturprüfung Baden-Württemberg: Mathematische Merkhilfe, 1. Auflage (2017)
S. 8/8
Wahrscheinlichkeit
Gegenereignis
P(A)  1  P(A)
Additionssatz
P(A  B)  P(A)  P(B)  P(A  B)
Spezieller Multiplikationssatz
P(A  B)  P(A)  P(B)
A , B unabhängig
Pfadregeln für Baumdiagramme
Die Wahrscheinlichkeiten längs eines Pfades werden multipliziert.
Die Wahrscheinlichkeiten der einzelnen Pfade werden addiert.
Erwartungswert einer Zufallsvariable X mit den Werten x1,x2 ,...,xn :
E(X)  x1  P(X  x1)  x2  P(X  x2 )  ...  xn  P(X  xn )
Binomialverteilung:
n
Formel von Bernoulli P(X  k)     pk  (1  p)nk
k 
E(X)  n  p
Erwartungswert
Statistische Tests
Beim Testen einer Hypothese H0 können folgende Fehler auftreten:
H0 ist wahr
H0 ist falsch
H0 wird verworfen
Fehler 1. Art
richtige Entscheidung
H0 wird nicht verworfen
richtige Entscheidung
Fehler 2. Art
Als Signifikanzniveau  bezeichnet man den Wert, den die Wahrscheinlichkeit für den
Fehler 1. Art nicht überschreiten darf.
Einseitiger Signifikanztest
Nullhypothese H0
Gegenhypothese H1
Ablehnungsbereich
linksseitiger Test
p  p0
p  p0
{0;1;...;g}
rechtsseitiger Test
p  p0
p  p0
{g;g  1;...;n}
Hinweis:
Die Merkhilfe stellt keine Formelsammlung im klassischen Sinn dar. Bezeichnungen werden nicht
erklärt und Voraussetzungen für die Gültigkeit der Formeln in der Regel nicht dargestellt.