1.3.8.5 Gekoppelte Schwingkreise verhalten sich wie gekoppelte

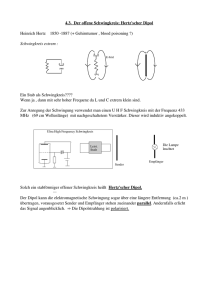
1.3.8.5 Gekoppelte Schwingkreise verhalten sich wie gekoppelte
mechanische Pendel
Zwei induktiv gekoppelte LC-Kreise verhalten sich analog zu zwei gekoppelten
Federn/Pendeln. Wie in der Mechanik kommt es zu einer Schwebung.
Wird der Kondensator des 1.
Kreises aufgeladen, fängt
dieser an zu schwingen. Über
die
Kopplung
(mttels
Eisenjoch
wie
beim
Transformator (oberes Bild)
oder
durch
Ineinanderschieben
der
Spulen (unteres Bild)) fängt
der 2. Kreis ebenfalls an zu
schwingen, wodurch dem 1.
Kreis (Schwingungs-)Energie
entzogen wird, bis nur noch
der 2. Kreis schwingt; dann
kehrt sich der Vorgang um.
Quelle: Staudt 2, Abb. 6.135, S.145
Schwebungen zeigen sich nur bei zwei nahe beieinander liegenden
Eigenfrequenzen. Wie bei den Federn sind diese dadurch charakterisiert, dass in
einem Fall die Systeme (Mechanik: Masse; hier: Ströme) in Phase (ϕ = 0°) bzw.
gerade in Gegenphase (ϕ = 180°) oszillieren. Die Schwebefrequenz ist wieder
ωSchwebung = ω2 – ω1.
1.3.8.6 Abstrahlung transversaler elektromagnetischer Wellen von einem
offenen Schwingkreis: Hertz’scher Dipol
Obwohl in einem Schwingkreis hochfrequente elektromagnetische Schwingungen
auftreten, ist er für eine Abstrahlung elektromagnetischer Wellen nicht geeignet;
d.h. sie bleiben im Schwingkreis gefangen und können sich nicht als Radio- oder
Fernsehwellen im Raum ausbreiten, da sich elektrisches und magnetisches Feld
fast ausschließlich im Inneren von Kondensator und Spule ausbilden. Um
elektromagnetische Wellen abstrahlen zu können, wird eine Antenne benötigt,
die auch „(Hertz’scher) Dipol“ genannt wird. (Mit Dipol ist nicht der elektrische µel
oder magnetische µmag Dipol gemeint.) Dabei handelt es sich um einen
gestreckten Leiter, der als „offener“ Schwingkreis angesehen werden kann, bei
dem Kapazität C und Induktivität L nicht mehr getrennt, sondern über den
ganzen Dipol gleichmäßig verteilt sind. Im gewissen Sinne ist ein solcher Dipol
damit die rudimentärste bzw. abstrahierte Form eines LC-Schwingkreises.
Übergang vom geschlossenen LC-Schwingkreis durch
dessen Vereinfachung und Öffnung zwischen den
Kondensatorplatten zu einem lang gestreckten Draht.
Quellen: Demtröder, Abb. 6-14, S170 und Physik
Gesamtband, S.184.
E5.17 gekoppelte
Schwingung
Beim „Öffnen" des Kondensators und dem Übergang von den
Kondensatorplatten und der Spule zu einem gestreckten Draht, dem Dipol bzw.
der (Dipol-)Antenne, verringern sich Kapazität und Induktivität der Anordnung
ganz erheblich. Ein Dipol hat damit eine höhere Eigenfrequenz als der LCSchwingkreis, aus dem man sich ihn entstanden denken kann.
Änderung des elektromgnetischen Feldverteilung beim Übergang vom LC-Schwingkreis (a) mit räumlich
begrenzten elektrischen und magnetischen Feldern über eine einzelne Leiterschleife (b) zum Dipol (c),
dem offenen Schwingkreis mit Feldern, die weit in den Raum hinausreichen (und sich vom Dipol ablösen
können). Quelle: Demtröder, Abb. 6.15, S.170.
Im LC-Schwingkreis werden die Elektronen durch die Spule hindurch periodisch
im Rhythmus der Hochfrequenz zwischen den Kondensatorplatten beschleunigt
(a). Im Dipol schwingen die Elektronen im Rhythmus der Hochfrequenz zwischen
den Dipolenden (c).
Zeitlicher Verlauf der E und B-Felder im Dipol. Quelle: Staudt, Abb. 6.141, S.152
Nach einer viertel Periode (t = 1/4T) besteht an einem Ende des Dipols ein
Elektronenüberschuss und am anderen ein Elektronenmangel. Zu diesem
Zeitpunkt existiert ein starkes elektrisches Feld (c: E-Feldlinien). Im mittleren Teil
des Dipols ist jeweils eine Viertelperiode später (t = 1/2T) die Stromstärke am
größten. Dabei schwingen die Elektronen am stärksten: Es besteht ein starkes
magnetisches Feld (c: B-Feldlinien).
Elektrische Feldlinien E und Magnetfeldlinien B stehen dabei immer senkrecht
aufeinander.
Wie bei einem geschlossenen Schwingkreis tritt auch bei einem Dipol eine
Phasenverschiebung zwischen Spannung U(t) und Stromstärke I(t) um eine
viertel Periode (1/4T) auf.
Wie lässt sich nun überhaupt eine Schwingung in
einem solchen geraden Draht (dem Dipol)
erzeugen? Der Dipol kann durch kapazitive oder
galvanische
Kopplung
oder
durch
elektromagnetische Induktion zum Schwingen
angeregt werden. Im letzteren Fall wird dazu der
mittlere Teil des Dipols vom Magnetfeld der Spule
eines separaten LC-Schwingkreises durchsetzt.
Induktive Kopplung eines LCDadurch kommt es zur Energieübertragung vom Kreises an einen Dipol der Länge l.
Schwingkreis auf den Dipol (s.a. Faraday’sches
Gesetz V11).
Ganz analog zur Erzeugung stehender
Wellen auf einer Violinen-Saite,
werden
bei
einer
bestimmten
Erregerfrequenz, der Eigenfrequenz ν0
des Dipols, im Dipol stehende
Stromwellen erzeugt. Diese Resonanz
tritt genau dann ein, wenn die halbe
Wellenlänge λ/2 der Erregung (oder
ein n-Faches davon) genau der Länge
l des Drahtes entspricht, d.h. für
l = n⋅
λErreger
2
mit
λ=
c
ν
=
Ausbreitungsgeschw. der Welle
Frequenz
wobei
c,
Ausbreitungsgeschwindigkeit,
Lichtgeschwindigkeit ist.
die
die
a) y-Auslenkung einer schwingenden Saite
(Mechanik) und stehende Stromwelle einer
Ladungs-Schwingung in einem geraden Draht
(Antenne, Dipol). Die Längen von Saite und Dipol
sind dabei halb so groß wie die Wellenlänge λ. Die
Stromverteilung I(z, t0) und die Spannungsverteilung
U(z, t0) sind für einen Zeitpunkt t0 angegeben. b) Der
Strombauch der stehenden Welle kann mit Hilfe von
Glühlämpchen bestätigt werden, die in der Mitte des
Dipols am hellsten leuchten, an den Enden
dagegen gar nicht. Quellen: Demtröder, Abb. 6.18,
S. 172 und Gesamtband Physik, S. 187.
M.a.W.: Schwingt ein Dipol mit seiner Eigenfrequenz, dann hat die
elektromagnetische Welle im Dipol eine Wellenlänge, die doppelt so lang wie der
Dipol ist. Beispiel: Abmessungen der Antenne eines Ultrakurzwellen (UKW)
Radiosenders [meist FM (frequency modulated)], der bei 92,0 MHz (gewöhnlich
zwischen 87 und 107 MHz) empfangen werden kann:
m
s ≈ 3,3 m .
λ=
6 1
92, 0 ⋅10
s
2,99 ⋅108
Quelle: Gesamtband Physik, S. 191
Die im Dipol erzeugten Wellen und daran geknüpften E- bzw. B-Felder können
sich vom Dipol ablösen und in den Raum ausbreiten.
Abschnüren geschlossener elektrischer Feldlinien (Wirbelfeld) vom Dipol und Ausbreitung im Raum.
Ablösen der magnetischen Feldlinien vom Dipol und Ausbreitung im Raum. Quelle: Physik Gesamtband,
S. 184.
Oszillation, Orientierung und Ablösen von E- und B-Feld. Quelle: Heywang, Physik für techn. Berufe,
S.361
Elektromagnetische (EM) Welle, (die sich vom Dipol der Länge h und vergleichsweise kleinen Breite dx
ablöst,) dargestellt durch einen Ausbreitungsstrahl in x-Richtung und zwei Wellenfronten, die eine
Wellenlänge λ voneinander entfernt sind. Darunter dieselbe Welle als „Schnappschuss“ der beiden
sinusförmig oszillierenden E- und B-Felder, die beide senkrecht zueinander und ebenfalls senkrecht zur
Ausbreitungsrichtung der Wellenfront stehen (E, B und Ausbreitungsrichtung folgen der Rechte-HandRegel): es handelt sich also um eine Transversalwelle (s.a. 1. Semester). Die Wellenfronten breiten sich
mit der Geschwindigkeit c aus, die der Lichtgeschwindigkeit entspricht. Fernfeld: E- und B-Feld sind in
weiter Entfernung zum Dipol nicht zueinander phasenverschoben: Wellenbäuche, Nulldurchgänge und
Wellentäler fallen also zeitlich zusammen. Nahfeld: In direkter Nähe zum Dipol, d.h. beim Ablöseprozess,
sind E- und B-Feld dagegen um 90° zueinander phasenverschoben, d.h. d.h. um eine viertel Periode T
zueinander versetzt (Wellenmaxima/-minima von E-Feld fallen mit Nulldurchgängen von B-Feld (magn.
Flussdichte) zusammen) (nicht gezeigt). Mit zunehmendem Abstand vom Dipol verringert sich diese
Phasenverschiebung, d.h. das Nahfeld geht kontinuierlich in das Fernfeld über. Quelle: Halliday, Abb. 345, S.971