Bahnradius - twintech.ch

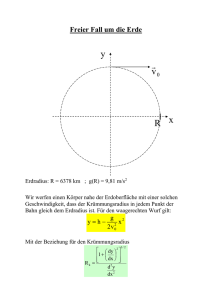
Bahnradius
Es soll die Bahn eines geworfenen Balls mit der Flugbahn eines Gewehrgeschosses verglichen werden.
Der Ball werde 10 Meter weit geworfen und erreiche dabei eine maximale Höhe von 2,5 Metern.
Mit dem Gewehr werde auf eine Distanz von 300 Metern geschossen. Wenn das Geschoss eine
Geschwindigkeit von 800 ms−1 hat, erreicht es eine maximale Höhe von 17 Zentimetern über der
Ziellinie. Der Luftwiderstand wird in beiden Fällen nicht berücksichtigt. Der Körper bewegt sich
somit „kräftefrei“ im Gravitationsfeld, d.h. ausser der Gravitationskraft wirkt keine andere Kraft
auf den Körper.
........................................................
..........
........
........
.......
......
.......
.....
......
.
.
.
.
.....
...
.
.....
.
.
...
....
.
.
.
....
.
..
.....
.........................................................................................................................................................................................................................
..............................................................................................................
..........................................................................................
.......................................................................................
..
Abbildung 1: Vergleich der Flugbahnen eines geworfenen Balls und eines
Gewehrgeschosses (nicht maßstäblich)
Es scheint offensichtlich zu sein, dass die Wurfbahn des Balls weitaus stärker gekrümmt ist als die
Flugbahn des Gewehrgeschosses.
Für eine flache Flugbahn kann die Bahn durch ein Kreisbogenstück approximiert werden. Damit
lässt sich der Krümmungsradius R der Bahn leicht berechnen (s. Abbildung 2).
......................................................................................................
................
....................
..............
................
...........
..............
...........
............
.
.
.
.
.
.
.
.
.
..........
.....
.
.
.
.
.
.......
.
.
.
.
...
h
A
A
s/2
A
A
A
A
A
A
A
A
A
A
A
A
A
¢
A ¢
A¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
¢
R
Abbildung 2: Krümmungsradius der Flugbahn
Krümmungsradius der Bahn eines kräftefreien Körpers in einem Gravitationsfeld
Wenn s die Wurfweite und h die Wurfhöhe bezeichnen, ergibt sich sofort
³ s ´2
2
(R − h) +
= R2 .
2
2
(1)
Ausmultiplizieren und Vereinfachen liefert:
−2 R h + h2 +
³ s ´2
2
= 0.
(2)
Für eine flache Flugbahn ist h2 ¿ R h, und der Term h2 kann vernachlässigt werden. Damit wird
R=
s2
.
8h
(3)
Diese auf Grund von Näherungen hergeleitete Beziehung liefert für den Scheitelpunkt einer Wurfparabel mit der Wufweite s und der Wurfhöhe h den richtigen Wert des Krümmungsradius. Sie
kann daher auch für den Ball verwendet werden, obwohl seine Flugbahn nicht flach ist.
Für die betrachteten Beispiele beträgt der Krümmungsradius der Wurfbahn des Balls 5 m, während
die Flugbahn des Gewehrgeschosses einen Krümmungsradius von über 66 km aufweist.
Werden die beiden Bahnen jedoch im vierdimensionalen Raum-Zeit-Kontinuum vergleichen, ergibt
sich ein völlig anderes Resultat 1 . Zu den drei Raumdimensionen mit den Achsen x, y und z
kommt die Zeitdimension hinzu, für die zweckmässigerweise nicht die Zeit t, sondern die mit der
Lichtgeschwindigkeit multiplizierte Zeit ct als Achse verwendet wird.
Während der Körper (beispielsweise) in Richtung der x-Achse fliegt, bewegt er sich zudem im
Raum-Zeit-Kontinuum in Richtung der ct-Achse. Die „Wurfweite“ d in der vierdimensionalen
Raum-Zeit ergibt sich aus der im dreimdimensionalen Raum gemessenen Wurfweite s durch
p
(4)
d = s2 + (c t)2 .
In den betrachteten Beispielen ist die während der Flugzeit t zurückgelegte Strecke ct weitaus
grösser als die in x-Richtung durchlaufene Strecke s. Näherungsweise gilt daher
d ≈ ct,
(5)
d2
8h
(6)
(c t)2
.
8h
(7)
und für den Krümmungsradius
R=
ergibt sich
R=
Die maximale Flughöhe h wird nach der halben Flugzeit erreicht, weshalb
µ ¶
g t 2
h=
2 2
(8)
gesetzt werden kann (g ist die Erdbeschleunigung). Damit wird
R=
c2
c2 t2
.
µ ¶2 =
g
g t
8
2 2
1
Ch.W. Misner, K.S. Thorne, J.A. Wheeler, „Gravitation“, W.H. Freeman and Company, New York, 1973,
S. 32.
(9)
Krümmungsradius der Bahn eines kräftefreien Körpers in einem Gravitationsfeld
3
Somit gilt allgemein für beliebige Wurfbahnen:
R=
c2
g
(10)
Wird mit R = R̃ c der Krümmungsradius durch die Lichtzeit R̃ ausgedrückt, ergibt sich:
c
.
g
(11)
2, 998 · 108
s = 3, 06 · 107 s .
9, 81
(12)
R̃ =
Mit c = 2, 998 · 108 ms−1 und g = 9, 81 ms−2 wird
R̃ =
In einem Gravitationsfeld mit einer Feldstärke von 9, 81 ms−2 haben also alle Wurfbahnen einen
Krümmungsradius von nahezu einem Lichtjahr (genauer: 354 Lichttage).
Es stellt sich die Frage, ob das auch für einen Satelliten gilt.
Für einen Satelliten, der die Erde auf einer Kreisbahn mit Radius r umfliegt, ist
m v2
= mg,
r
(13)
wobei g hier als die im Abstand r vom Erdzentrum herrschende Gravitationsfeldstärke betrachtet
werden kann. Daraus ergibt sich für die Geschwindigkeit:
v=
√
gr.
(14)
t=
2πr
,
v
(15)
r
(16)
Die Umlaufszeit ist
also
t = 2π
r
.
g
Im vierdimensionalen Raum-Zeit-Kontinuum beschreibt der Satellit eine Schraubenlinie um die
ct-Achse.
ct
r
2π h
Abbildung 3: Satellitenbahn im vierdimensionalen Raum-Zeit-Kontinuum
Krümmungsradius der Bahn eines kräftefreien Körpers in einem Gravitationsfeld
4
Wird die Ganghöhe mit 2 π h bezeichnet, gilt für den Krümmungsradius der Schraubenlinie die
Beziehung
r2 + h2
R=
.
(17)
r
Die Ganghöhe ist gleich c t:
2πh = ct.
(18)
Also gilt
ct
,
2π
und daher ist für einen Satelliten r ¿ h. Deshalb kann R durch
h=
R=
h2
r
(19)
(20)
approximiert werden. Einsetzen der Gleichungen (19) und (16) liefert
R=
c2 4 π 2 r
c2
c2 t2
=
=
,
4 π2 r
4 π2 r g
g
(21)
also wieder die allgemeine Beziehung (10). Die Beziehung gilt also tatsächlich auch für einen
Satelliten.
Anhang
Krümmungsradius einer Raumkurve
Eine Raumkurve kann durch
~r = ~r(t) = (x(t), y(t), z(t))
(22)
dargestellt werden. Die Richtung der Tangente an die Kurve wird durch den Tangentenvektor
dx dy dz
d~r
= (ẋ, ẏ, ż) = ( , , )
~r˙ =
dt
dt dt dt
gegeben, dessen Betrag sich aus
sµ ¶
µ ¶2 µ ¶2
p
dx 2
dy
dy
1p
ds
2
˙
˙
|~r | = ~r =
+
+
=
(dx)2 + (dy)2 + (dz)2 ) =
dt
dt
dt
dt
dt
(23)
(24)
ergibt. s ist die Bogenlänge. Es gilt somit:
dt
1
=
.
ds
|~r˙ |
(25)
Der Ortsvektor kann als Funktion der Bogenlänge betrachtet werden:
~r = ~r(s) .
(26)
Die Ableitung des Ortsvektors nach der Bogenlänge ist
~r 0 =
d~r
d~r dt
1
=
= ~r˙
.
ds
dt ds
|~r˙ |
(27)
Krümmungsradius der Bahn eines kräftefreien Körpers in einem Gravitationsfeld
5
Somit ist
der Vektor ~r 0 ist ein Einheitsvektor.
Die Krümmung ist definiert als
Da
|~r 0 | = 1 ,
(28)
κ = |~r 00 | .
(29)
2
¯ 0¯
¯
¯ 0
¯
¯
¯
¯ ¯ ¯
¯ d~r ¯
¯ ∆~r 0 ¯
¯ ~r ∆ϕ ¯
¯ ∆ϕ ¯ ¯ dϕ ¯
¯
¯
¯
¯
¯
¯
¯
¯=¯ ¯,
κ = |~r | = ¯
= lim
= lim
= lim
ds ¯ ∆s→0 ¯ ∆s ¯ ∆s→0 ¯ ∆s ¯ ∆s→0 ¯ ∆s ¯ ¯ ds ¯
00
(30)
kann die Krümmung als Drehgeschwindigkeit der Tangente (Winkeländerung pro Bogenlänge) interpretiert werden.
Die Ableitung von
wird
1
1
dt
=p
=
˙
ds
|~r |
~r˙ 2
˙¨
d2 t
1 1
˙ ~¨r dt = − ~r ~r .
=
−
2
~
r
ds2
2 (~r˙ )3/2
ds
~r˙ 2
(31)
(32)
Damit ergibt sich für die Ableitung von
dt
~r 0 = ~r˙
ds
der Ausdruck
~r = ~¨r
00
µ
dt
ds
¶2
~¨r
~r˙ ~¨r ˙
d2 t
−
~r .
+ ~r˙ 2 =
ds
~r˙ 2 ~r˙ 2
(33)
(34)
Kreis
Ein Kreis kann durch
~r = (r cos t, r sin t)
(35)
~r˙ = (−r sin t, r cos t)
(36)
~¨r = (−r cos t, −r sin t) .
(37)
~r˙ 2 = r2 sin2 t + r2 cos2 t = r2
(38)
~r˙ ~¨r = r2 sin t cos t − r2 cos t sin t = 0 .
(39)
dargestellt werden.
Die Ableitungen sind
und
Damit wird
und
Somit ist
~r 00 =
und
(~r 00 )2 =
(−r cos t, −r sin t)
r2
r2 cos2 t + r2 sin2 t
1
= 2.
r4
r
(40)
(41)
2
Siehe z.B.: B. Klotzek, „Einführung in die Differentialgeometrie“, Verlag Harri Deutsch, Thun und Frankfurt
am Main, 1977.
Krümmungsradius der Bahn eines kräftefreien Körpers in einem Gravitationsfeld
Für die Krümmung
κ = |~r 00 | =
ergibt sich damit die Beziehung
p
(~r 00 )2
6
(42)
1
.
r
Die Krümmung eines Kreises ist gleich dem Reziprokwert des Kreisradius.
κ=
(43)
Wurfparabel
y
...................................
................
..........
..........
........
.......
......
......
......
.
.
.
.
.
.....
....
.
.....
.
.
.....
...
.
.
.
.....
..
.
.
.
.
....
....
x
Abbildung 4: Wurfparabel
Eine Wurfparabel mit der Wurfweite s und der Wurfhöhe h wird durch die Gleichung
y=−
4h 2 4h
x
x +
s2
s
(44)
oder die Parameterdarstellung
~r = (t, −
4h 2 4h
t +
t)
s
s
(45)
beschrieben. Aus (45) folgt
und
8h
4h
~r˙ = (1, − 2 t +
)
s
s
(46)
8h
~¨r = (0, − 2 ) .
s
(47)
~r˙ = (1, 0)
(48)
~r˙ ~¨r = 0 .
(49)
An der Stelle t = s/2 ist
und
Damit ergibt sich aus (29) und (34)
8h
.
(50)
s2
Der Krümmungsradius R ist definiert als der Radius eines Kreises mit gleicher Krümmung. Somit
ist
s2
.
(51)
R=
8h
κ = |~r 00 | =
Krümmungsradius der Bahn eines kräftefreien Körpers in einem Gravitationsfeld
7
Schraubenlinie
Eine Schraubenlinie wird durch die Parameterdarstellung
~r = (r cos t, r sin t, h t)
(52)
gegeben. Die Ganghöhe ist 2 π h. Für die Ableitungen ergibt sich
~r˙ = (−r sin t, r cos t, h)
(53)
~¨r = (−r cos t, −r sin t, 0) .
(54)
~r˙ 2 = r2 sin2 t + r2 cos2 t + h2 = r2 + h2
(55)
~r˙ ~¨r = r2 sin t cos t − r2 cos t sin t = 0 .
(56)
und
Es folgt
und
Einsetzen der Gleichungen (54), (55) und (56) in die Beziehung (34) ergibt
~r 00 =
(−r cos t, −r sin t, 0)
.
r 2 + h2
(57)
Quadrieren liefert
(~r 00 )2 =
r2 cos2 t + r2 sin2 t
r2
=
.
(r2 + h2 )2
(r2 + h2 )2
(58)
Damit ergibt sich schliesslich für die Krümmung die Beziehung
κ=
r
.
r2 + h2
(59)
R=
r2 + h2
.
r
(60)
Somit ist
16. Juni 2009
A. Ruh