Übungsfolien - WWZ - Universität Basel

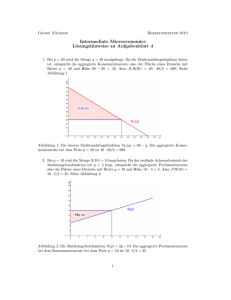
Übung 4: Gleichgewicht und Effizienz in
Wettbewerbsmärkten
Georg Nöldeke
Wirtschaftswissenschaftliche Fakultät, Universität Basel
Intermediate Microeconomics HS 11
Übung 4
1 / 35
Marktnachfrage und aggregierte Konsumentenrente
Aufgabe 1
Worum geht es?
Sie verstehen, wie man die aggregierte Konsumentenrente in einem
Wettbewerbsmarkt aus der Marktnachfragefunktion bzw. aus der
inversen Marktnachfragefunktion bestimmt.
In einem Wettbewerbsmarkt ist die aggregierte
Konsumentenrente KR(p) gleich der Fläche zwischen Preis und
Marktnachfragefunktion bis zu der Menge, die bei dem Preis p
nachgefragt wird.
In Berechnungen wird durchweg das Beispiel einer linearen
Marktnachfragefunktion betrachtet, bei der KR(p) als
Dreiecksfläche bestimmt werden kann.
2 / 35
Marktnachfrage und aggregierte Konsumentenrente
Aufgabe 1
Abbildung: Die inverse Marktnachfragefunktion PD (q) = 60 − q. Die
aggregierte Konsumentenrente bei dem Preis p = 20 ist 40 · 40/2 = 800.
3 / 35
Marktangebot und aggregierte Produzentenrente
Aufgabe 2
Worum geht es?
Sie verstehen, wie man die aggregierte Produzentenrente in einem
Wettbewerbsmarkt aus der Marktangebotsfunktion bzw. aus der
inversen Marktangebotsfunktion bestimmt.
In einem Wettbewerbsmarkt ist die aggregierte Produzentenrente
PR(p) gleich der Fläche zwischen Marktangebotsfunktion und
Preis bis zu der Menge, die bei dem Preis p angeboten wird.
In Berechnungen wird durchweg das Beispiel einer linearen
Marktangebotsfunktion betrachtet, bei der PR(p) als
Dreiecksfläche bestimmt werden kann.
4 / 35
Marktangebot und aggregierte Produzentenrente
Aufgabe 2
Abbildung: Die Marktangebotsfunktion S(p) = 2p − 10. Die aggregierte
Produzentenrente bei dem Konsumentenrente bei dem Preis p = 10 ist
10 · 5/2 = 25.
5 / 35
Marktangebot und aggregierte Produzentenrente
Aufgabe 3
Worum geht es?
Sie verstehen, wie man die Marktangebotsfunktion aus Angaben über
die Anzahl der Unternehmen und ihre Kostenfunktionen bestimmt.
1
Aus den Kostenfunktionen erhält man die Angebotsfunktionen der
einzelnen Unternehmen.
2
Aus Addition der einzelnen Angebotsfunktionen erhält man die
Marktangebotsfunktion.
Achtung: Niemals inverse Angebotsfunktionen addieren, um die
inverse Marktangebotsfunktion zu bestimmen!
6 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 4
Worum geht es?
Sie verstehen, wie eine Veränderung eines Mengensteuersatzes den
aggregierten Handelsgewinn und seine Bestandteile beeinflusst und
können in dem Beispiel linearer Marktangebots- und
Marktnachfragefunktionen entsprechende Berechnungen anstellen.
Aggregierte Konsumentenrente ist fallend in τ.
Aggregierte Produzentenrente ist fallend in τ.
Steuereinnahmen sind zuerst steigend, dann fallend in τ.
Aggregierte Handelsgewinne sind fallend in τ.
Auswirkung einer Erhöhung des Steuersatzes auf die
aggregierten Handelsgewinne ist um so grösser, je höher der
Steuersatz bereits ist.
7 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 4(a)
Berechnungen im linearen Beispiel:
1
Um zu bestimmen, wie
die aggregierte Konsumentenrente
die aggregierte Produzentenrente
die Steuereinnahmen
von τ abhängen, ist zuerst das Wettbewerbsgleichgewicht mit
Besteuerung zu bestimmen: q ∗ (τ), pd∗ (τ), ps∗ (τ).
2
Anschliessend bestimmt man
die aggregierte Konsumentenrente mit der Formel für die
entsprechende Dreiecksfläche bei Menge q ∗ (τ) und Preis pd∗ (τ).
die aggregierte Produzentenrente mit der Formel für die
entsprechende Dreiecksfläche bei Menge q ∗ (τ) und Preis ps∗ (τ).
die Steuereinnahmen als Produkt τ · q ∗ (τ).
8 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 4(b)
Aggregierte Handelsgewinne und Zusatzlast
Die aggregierten Handelsgewinne mit Besteuerung sind als
HG∗ (τ) = KR ∗ (τ) + PR ∗ (τ) + T ∗ (τ)
definiert.
Die Zusatzlast der Besteuerung ist der Verlust an aggregierten
Handelsgewinnen, der im Vergleich zu dem
Wettbewerbsgleichgewicht ohne Besteuerung entsteht:
Z (τ) = HG∗ (0) − HG∗ (τ).
Die Zusatzlast kann auch direkt durch Flächenbestimmung
berechnet werden, da sie einem Dreieck mit Höhe τ und Länge
q ∗ (0) − q ∗ (τ) entspricht.
9 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 4(b)
Beachte:
Alle Formeln, die in dieser Aufgabe berechnet wurden, gelten
ohne Änderung für Mengensubventionen.
Dabei −τ > 0 der Satz, mit dem jede Einheit subventioniert wird.
10 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 5
Abbildung: Wettbewerbsgleichgewicht mit fixem Angebot.
11 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 5
Abbildung: Bei fixem Angebot entsteht keine Zusatzlast der Besteuerung, da
die Mengensteuer keinen Einfluss auf die Allokation des Gutes hat.
12 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6
Worum geht es?
Sie verstehen die Wohlfahrtsverluste, die durch Stützungspreise und
Ausgleichszahlungen verursacht werden und können Sie in Beispielen
mit linearer Marktangebots- und Marktnachfragefunktion berechnen.
13 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(a)
Wettbewerbsgleichgewicht
Marktnachfragefunktion (im relevanten Bereich): D(p) = 100 − p
Marktangebotsfunktion: S(p) = 3p.
Wettbewerbspreis: D(p∗ ) = S(p∗ ) ⇒ p∗ = 25.
Wettbewerbsmenge: q ∗ = D(25) = S(25) = 75.
Aggregierte Handelsgewinne im Wettbewerbsgleichgewicht =
Aggregierte Produzentenrente im GG + Aggregierte
Konsumentenrente im GG.
Aggregierte Produzentenrente: PR(25) = 75 · 25/2
Aggregierte Konsumentenrente: KR(25) = 75 · 75/2
Aggregierte Handelsgewinne = 75 · 100/2 = 3750.
14 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(a)
Abbildung: Wettbewerbspreis, Wettbewerbsmenge, aggregierte
Konsumentenrente und aggregierte Produzentenrente zu Aufgabe 6(a). Die
aggregierten Handelsgewinne sind die Summe aus aggregierter
Konsumenten- und Produzentenrente.
15 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(b)
Unterstützungspreis (mit Vernichtung des Überschusses):
Preis auf p = 30 festgesetzt.
Überschussangebot wird vom Staat aufgekauft.
Differenz zwischen angebotener und nachgefragter Menge wird
vernichtet.
Frage: Staatliche Ausgaben?
Antwort: 30 · [S(30) − D(30)].
16 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(b)
Abbildung: Angebotene und nachgefragte Menge bei p = 30 und die
resultierenden Staatsausgaben (schraffierte Fläche) zu Aufgabe 6(b). Die
Staatsausgaben sind 30 · [S(30) − D(30)] = 30 · 20 = 600.
17 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(b)
Wohlfahrtsanalyse:
PR(30) = 30 · 90/2 = 1350.
KR(30) = 70 · 70/2 = 2450.
Die aggregierten Handelsgewinne sind:
HG = KR(30) + PR(30) − 600 = 3200.
Im Vergleich zu der Wettbewerbssituation sind die aggregierten
Handelsgewinne also um 550 gefallen.
18 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(b)
Abbildung: Die grüne Fläche stellt den Wohlfahrtsverlust zu Aufgabe 6(b) dar.
Dieses ist der Teil der Staatsausgaben, dem kein Zugewinn an Rente
gegenüber steht. Der Zugewinn an Rente in Höhe von 50 ist die Fläche des
verbleibenden, schraffierten Dreiecks.
19 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(c)
Ausgleichszahlung:
Produzenten verkaufen Menge S(30) = 90.
Bestimmung des Gleichgewichtspreis: D(p) = 90 ⇒ p = 10.
Bestimmung der Staatsausgaben: 90 · [30 − 10] = 1800.
Für die Wohlfahrtsanalyse wird noch benötigt: KR(10) = 4050.
Die aggregierten Handelsgewinne sind
KR(10) + PR(30) − 1800 = 3600.
20 / 35
Markteingriffe und Wohlfahrtsverlust
Aufgabe 6(c)
Abbildung: Grafische Darstellung zu Aufgabe 6(c): Bei p̃ = 10 entspricht die
durch die Konsumenten nachgefragte Menge der zum Preis p = 30
angebotenen Menge. Die Staatsausgaben entsprechen der schraffierten
Fläche. Der Wohlfahrtsverlust ist die grüne Fläche.
21 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 7
Worum geht es?
Bedingung für profitablen Marktzutritt mit quasifixen Kosten verstehen
und anwenden können.
1
Marktzutritt ist profitabel, wenn der Outputpreis grösser als die
minimalen Durchschnittskosten eines aktiven Unternehmens sind.
2
Marktzutritt ist profitabel, wenn die kurzfristige Produzentenrente
eines aktiven Unternehmens grösser als die Kosten des
Marktzutritts sind.
22 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 7
Zwei Lösungsansätze:
1
Bestimme die effiziente Betriebsgrösse ŷ eines aktiven
Unternehmens und die damit verbundenen Durchschnittskosten
AC(ŷ ). Gilt p ≥ AC(ŷ ) ist Marktzutritt optimal.
2
Bestimme die kurzfristige Angebotsmenge s(p) eines aktiven
Unternehmens bei p. Gilt p · s(p) − VC(s(p)) ≥ F , so ist
Marktzutritt optimal.
23 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 7
In dieser Aufgabe ist der zweite Lösungsansatz einfacher.
Grenzkosten: MC(y ) = 40 + 100y .
Grenzkosten gleich Preis p = 140 setzen ⇒ y = 1.
Resultierende Produzentenrente 140 − VC(1) = 140 − 90 = 50.
Da 50 < F = 80 ist ist es besser, inaktiv zu sein.
24 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8
Worum geht es?
Bestimmung von kurzfristigen Wettbewerbsgleichgewicht sowie
langfristigen Wettbewerbsgleichgewicht mit Marktzutritt.
Kochrezept für langfristiges Wettbewerbsgleichgewicht mit Marktzutritt:
1
2
3
4
Bestimme die effiziente Betriebsgrösse ŷ eines aktiven
Unternehmens.
Bestimme die dazugehörigen minimalen Durchschnittskosten p̂.
Dieses ist der langfristige Wettbewerbspreis p∗ = p̂
Bestimme die bei p∗ nachgefragte Menge. Dieses ist die
langfristige Wettbewerbsmenge: q ∗ = D(p∗ )
Teile q ∗ durch ŷ, um die Anzahl der aktiven Unternehmen zu
bestimmen: m∗ = q ∗ /ŷ.
25 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8
Kostenfunktion für aktive Unternehmen:
C(y ) = 100 + 100y + 4y 2 .
Marktnachfragefunktion (im relevanten Bereich): D(p) = 1000 − p.
Kurzfristiges Wettbewerbsgleichgewicht in Abhängigkeit von der
Anzahl m der aktiven Unternehmen?
Langfristiges Wettbewerbsgleichgewicht?
26 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(a)
Bestimmung des kurzfristigen Wettbewerbsgleichgewichts:
Grenzkostenfunktion eines aktiven Unternehmen bestimmen:
MC(y ) = 100 + 8y .
Gleichung p = MC(y) nach y auflösen: Angebotsfunktion eines
Unternehmens im relevanten Bereich: s(p) = (p − 100)/8.
Angebotsfunktion eines Unternehmens mit Anzahl der
Unternehmen multiplizieren: Marktangebotsfunktion mit m aktiven
Unternehmen:
p − 100
Sm (p) = m
8
Kurzfristiges Wettbewerbsgleichgewicht mit
Marktnachfragefunktion und Marktangebotsfunktion bestimmen:
∗
pm
=
8000 + 100m
900m
∗
, qm
=
.
m+8
m+8
27 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(a)
Abbildung: Marktnachfragefunktion und kurzfristige Marktangebotsfunktionen
für m = 20, m = 50 und m = 100. Kurzfristiger Wettbewerbspreis und
Wettbewerbsmenge liegen in dem jeweiligen Schnittpunkt der kurzfristigen
Marktangebotsfunktionen mit der Marktnachfragefunktion.
28 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(b)
Bestimmung des langfristigen Wettbewerbsgleichgewichts:
1
Bestimme die effiziente Betriebsgrösse: ŷ = 5.
2
Bestimme die minimalen Durchschnittskosten: p̂ = 140
3
Bestimme die Menge, die bei p̂ nachgefragt wird: q ∗ = 860.
4
Bestimme die Anzahl der Unternehmen, die erforderlich sind, um
q ∗ zu minimalen Durchschnittskosten zu produzieren: m∗ = 172.
29 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(b)
Abbildung: Der kurzfristige Wettbewerbspreis als Funktion der Anzahl der
aktiven Unternehmen in Relation zu den minimalen Durchschnittskosten.
m∗ = 172.
30 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(b)
Ein alternativer Lösungsansatz:
Aus der Angebotsfunktion eines aktiven Unternehmens lässt sich
die kurzfristige Produzentenrente eines solchen Unternehmens
bei Preis p als Dreiecksfläche bestimmen:
(p − 100)
1
1
=
(p − 100)2 .
pr = (p − 100) ·
2
8
16
Im langfristigen Wettbewerbsgleichgewicht erzielen die aktiven
Unternehmen Nullgewinne, so dass die Produzentenrente den
Marktzutrittskosten entsprechen muss:
1 ∗
(p − 100)2 = 100 ⇒ p∗ = 140.
16
q ∗ und m∗ können dann wie zuvor aus der
Marktnachfragefunktion bestimmt werden.
Beachte: Dieser Ansatz ist insbesondere dann nützlich, wenn es
keine explizite Information zur Kostenfunktion gibt.
31 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(c)
Komparative Statik des langfristigen Wettbewerbsgleichgewichts:
Eine Verschiebung der Marktnachfragefunktion lässt die
minimalen Durchschnittskosten und damit p∗ sowie die
Gleichgewichtsproduktionsmenge eines einzelnen Unternehmens
unverändert. Jedoch wird sich die Gleichgewichtsmenge und
damit die Anzahl der aktiven Unternehmen ändern.
Eine Verschiebung der Kostenfunktion ändert die effiziente
Betriebsgrösse und die minimalen Durchschnittskosten, so dass
die Auswirkungen auf alle Gleichgewichtsbedingungen zu
untersuchen sind.
32 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 8(c)
Beispiel: Anstieg der Marktzutrittskosten auf Grund einer Gebühr.
Die effiziente Betriebsgrösse sowie die minimalen
Durchschnittskosten steigen an.
Also steigt der Gleichgewichtspreis.
Die Gleichgewichtsmenge sowie die Gleichgewichtsanzahl der
aktiven Unternehmen fallen.
Zusatzfrage: Was sind die Wohlfahrtsauswirkungen?
Langfristige Produzentenrente bleibt unverändert (gleich Null).
Aggregierte Konsumentenrente fällt.
Es entstehen Staatseinnahmen durch die Gebühren.
Der Gesamteffekt auf die Handelsgewinne ist negativ.
33 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 9
Worum geht es?
Bestimmung der Produzentenrente aus der Angebotsfunktion
eines Unternehmens.
Verwendung dieser Information zur Bestimmung des langfristigen
Wettbewerbsgleichgewichts.
34 / 35
Langfristiges Marktgleichgewicht und Marktzutritt
Aufgabe 9
Angebotsfunktion eines aktiven Unternehmens ist s(p) = p.
Kurzfristige Produzentenrente eines aktiven Unternehmens ist
somit pr (p) = p2 /2.
Aus der Bedingung pr (p) = F folgt hier p∗ = 2.
Aus D(2) = 8 und s(2) = 2 folgt, dass im langfristigen
Wettbewerbsgleichgewicht 4 Unternehmen aktiv sind.
35 / 35