Intermediate Microeconomics Lösungshinweise zu

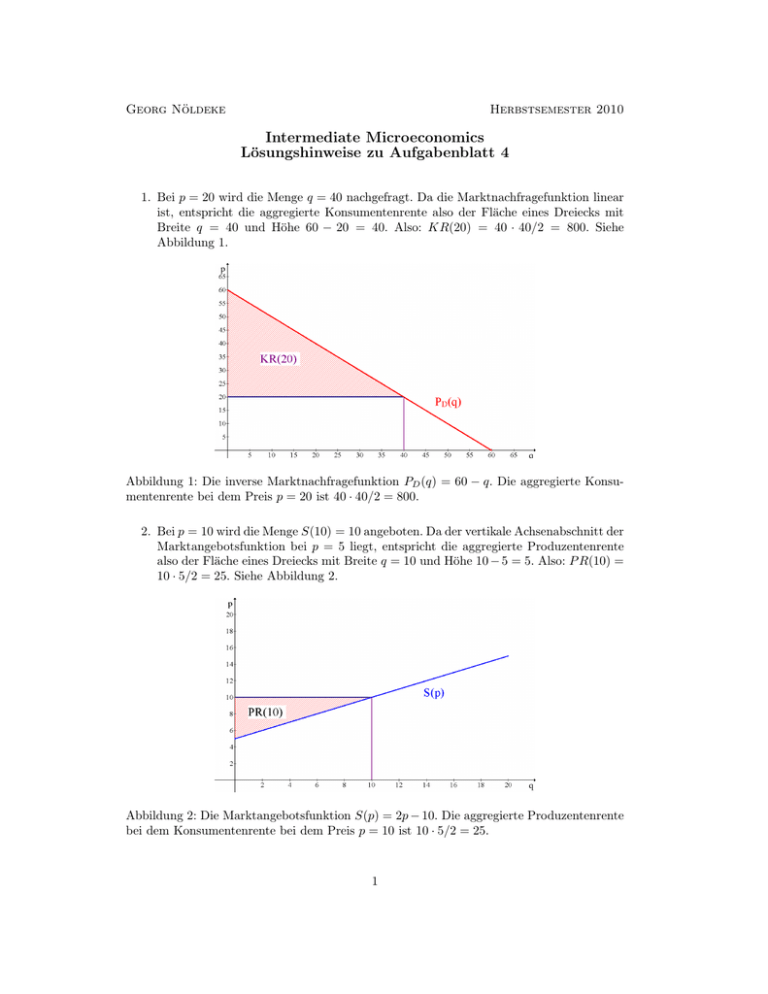
Georg Nöldeke
Herbstsemester 2010
Intermediate Microeconomics
Lösungshinweise zu Aufgabenblatt 4
1. Bei p = 20 wird die Menge q = 40 nachgefragt. Da die Marktnachfragefunktion linear
ist, entspricht die aggregierte Konsumentenrente also der Fläche eines Dreiecks mit
Breite q = 40 und Höhe 60 − 20 = 40. Also: KR(20) = 40 · 40/2 = 800. Siehe
Abbildung 1.
Abbildung 1: Die inverse Marktnachfragefunktion PD (q) = 60 − q. Die aggregierte Konsumentenrente bei dem Preis p = 20 ist 40 · 40/2 = 800.
2. Bei p = 10 wird die Menge S(10) = 10 angeboten. Da der vertikale Achsenabschnitt der
Marktangebotsfunktion bei p = 5 liegt, entspricht die aggregierte Produzentenrente
also der Fläche eines Dreiecks mit Breite q = 10 und Höhe 10 − 5 = 5. Also: P R(10) =
10 · 5/2 = 25. Siehe Abbildung 2.
Abbildung 2: Die Marktangebotsfunktion S(p) = 2p − 10. Die aggregierte Produzentenrente
bei dem Konsumentenrente bei dem Preis p = 10 ist 10 · 5/2 = 25.
1
3. Die Grenzkostenfunktion eines jeden Unternehmens ist M C(y) = 6y, so dass die Angebotsfunktion eines Unternehmens s(p) = p/6 ist. Da es 24 solcher Unternehmen
gibt, ist die Marktangebotsfunktion S(p) = 4p. Aus der Markträumungsbedingung
D(p∗ ) = S(p∗ ) folgt p∗ = 6.
4. Die Gleichgewichtsmenge q ∗ (τ ) ist durch die Lösung der Gleichung PD (q ∗ (τ ))−PS (q ∗ (τ )) =
τ gegeben. Also:
A−τ
.
A − aq ∗ (τ ) − bq ∗ (τ ) = τ ⇒ q ∗ (τ ) =
a+b
Der resultierende Konsumentenpreis ist
p∗d (τ ) = PD (q ∗ (τ )) =
bA + aτ
.
a+b
Der resultierende Produzentenpreis ist
p∗s (τ ) = PS (q ∗ (τ )) =
bA − bτ
.
a+b
(a) Die aggregierte Konsumentenrente bei dem Steuersatz τ ist (Dreiecksflächenberechnung!)1
2
a A−τ
1 A − τ a(A − τ )
∗
∗
∗
=
.
KR (τ ) = q (τ ) · (A − pd (τ ))/2 =
2 a+b a+b
2 a+b
Für die aggregierte Produzentenrente bei dem Steuersatz τ erhält man entsprechend:
2
b A−τ
P R∗ (τ ) = q ∗ (τ ) · p∗s (τ )/2 =
.
2 a+b
Die Steuereinnahmen sind
T ∗ (τ ) = q ∗ (τ ) · τ = τ
A−τ
.
a+b
Siehe hierzu auch Abbildung 3.
(b) Die Zusatzlast der Besteuerung entspricht der Differenz zwischen den aggregierten Handelsgewinnen im Wettbewerbsgleichgewicht ohne Besteuerung und den
aggregierten Handelsgewinnen in der Situation mit Besteuerung und kann entsprechend berechnet werden. Die aggregierten Handelsgewinne im Wettbewerbsgleichgewicht lassen sich dadurch bestimmen, dass man in die Formeln aus der
vorhergehenden Teilaufgabe τ = 0 einsetzt. Man erhält:
HG∗ (0) = KR∗ (0) + P R∗ (0) =
1 A2
.
2a+b
Die aggregierten Handelsgewinne in der Situation mit Besteuerung sind
HG∗ (τ ) = KR∗ (τ ) + P R∗ (τ ) + T ∗ (τ ) =
1 (A − τ )2 + 2τ (A − τ )
1 A2 − τ 2
=
.
2
a+b
2 a+b
Die Zusatzlast der Besteuerung ist daher
Z(τ ) = HG∗ (0) − HG∗ (τ ) =
1 τ2
.
2a+b
1 Die folgende Berechnung lässt sich vereinfachen, wenn man bemerkt, dass der Preis p∗ (τ ) um den Betrag
d
a · q ∗ (τ ) unterhalb von A liegen muss. Also ist die aggregierte Konsumentenrente durch aq ∗ (τ )2 /2 gegeben.
2
Abbildung 3: Die Bestandteile der aggregierten Handelsgewinne und die Zusatzlast als Funktion des Steuersatzes. Die Grafik stellt einen Fall mit b = 3a dar, so dass die aggregierte
Produzentenrente das Dreifache der aggregierten Konsumentenrente beträgt.
Siehe hierzu auch Abbildung 3.
Einfacher als durch den obigen Rechenansatz kann die Zusatzlast als Dreiecksfläche bestimmt werden. Grafisch ist die Zusatzlast der Besteuerung durch ein
Dreieck mit der Höhe τ und Breite q ∗ (0) − q ∗ (τ ) = τ /(a + b) gegeben. Die entsprechende Dreiecksfläche entspricht gerade dem zuvor berechneten Wert von
Z(τ ).
(c) Die Ableitung der Zusatzlast ist
Z 0 (τ ) =
τ
.
a+b
Für τ > 0 ist diese Ableitung streng positiv. Dieses besagt, dass die Zusatzlast
um so grösser ist, je höher der Steuersatz ist. Zudem ist die Ableitung steigend
in τ . Dieses besagt, dass der Wohlfahrtsverlust aus der Erhöhung der Steuer um
eine Einheit um so grösser ist, je höher der Ausgangssteuersatz ist. Für τ = 0
gilt Z 0 (τ ) = 0. Dieses bedeutet, dass die Einführung einer kleinen Mengensteuer fast keinen Wohlfahrtsverlust verursacht. (Der Grund ist, dass die marginale
Zahlungsbereitschaft der Konsumenten im Wettbewerbsgleichgewicht ohne Besteuerung mit den Grenzkosten der Unternehmen übereinstimmt, so dass durch
eine kleine Reduktion der gehandelten Mengen kaum Handelsgewinne verloren
gehen.) Zuletzt ist noch bemerkenswert, dass der Anstieg der Zusatzlast (und die
Zusatzlast selbst) um so geringer ist, je grösser die Steigung der inversen Marktnachfragefunktion und der inversen Marktangebotsfunktion ist. (Der Grund ist,
dass die Mengenänderung, die durch eine Erhöhung der Steuer ausgelöst wird,
um so geringer ist, je steiler diese Funktionen verlaufen.)
5. Ist das Angebot vollkommen unelastisch, so lässt die Einführung einer Mengensteuer die aggregierten Handelsgewinne unverändert. Die aggregierte Konsumentenrente
bleibt unverändert, da der Konsumentenpreis unverändert bleibt. Die aggregierte Produzentenrente fällt genau um den Betrag der Steuereinnahmen.
6. (a) Der Wettbewerbspreis ist durch die Bedingung D(p∗ ) = S(p∗ ) bestimmt. Hier
3
also:
100 − p∗ = 3p∗ ⇒ p∗ = 25.
Die Wettbewerbsmenge ist die Menge, die zum Wettbewerbspreis sowohl nachgefragt wie angeboten wird, q ∗ = D(p∗ ) = S(p∗ ). Hier also
q ∗ = 75.
Abbildung 4: Wettbewerbspreis, Wettbewerbsmenge und aggregierter Handelsgewinne (als
Summe von aggregierter Konsumentenrente und aggregierter Produzentenrente beim Wettbewerbspreis) zu Aufgabe 6 (a).
Die aggregierten Handelsgewinne in einem Wettbewerbsgleichgewicht entsprechen
der Summe aus aggregierter Konsumentenrente und aggregierter Produzentenrente zum Wettbewerbspreis und damit der Fläche zwischen der inversen Marktnachfragefunktion und der inversen Marktangebotsfunktion bis zur Menge q ∗ . Diese
Fläche kann man wie folgt bestimmen: Die aggregierte Konsumentenrente bei
p∗ = 25 ist ein rechtwinkliges Dreieck mit Höhe 75 und Länge 75, so dass
KR∗ = 75 · 75/2
gilt. Die aggregierte Produzentenrente bei p∗ = 25 ist ein rechtwinkliges Dreieck
mit Höhe 25 und und Länge 75, so dass
P R∗ = 75 · 25/2
gilt. Addiert man die beiden Ausdrücke erhält man
HG∗ = 75 · 100/2 = 3750.
4
(b) Bei dem Unterstützungspreis p = 30 werden S(30) = 90 Einheiten angeboten und
D(30) = 70 Einheiten nachgefragt. Der Staat muss also 20 Einheiten zum Preis
von 30 aufkaufen. Die resultierenden Ausgaben sind 600.
Die aggregierte Produzentenrente ist
P R(30) = 30 · 90/2 = 1350.
Die aggregierte Konsumentenrente ist
KR(30) = 70 · 70/2 = 2450.
Die Staatsausgaben wurden bereits als 600 bestimmt, so dass die aggregierten
Handelsgewinne
HG = 1350 + 2450 − 600 = 3200
betragen. Im Vergleich zum Wettbewerbsgleichgewicht werden die aggregierten
Handelsgewinne also um 550 Einheiten reduziert. (Anders gesagt: Die staatlichen
Ausgaben in Höhe von 600 erhöhen die Summe von aggregierter Konsumentenund Produzentenrente lediglich um 50 Einheiten.)
Abbildung 5: Angebotene und nachgefragte Menge bei p = 30 und die resultierenden Staatsausgaben (schraffierte Fläche) zu Aufgabe 6 (b).
(c) Der Wettbewerbspreis in dieser Situation ist p̃ = 10, da hier D(p̃) = S(30) = 90
gilt. Der Staat muss also eine Ausgleichszahlung von 30 − 10 = 20 Geldeinheiten
auf 90 Einheiten leisten, so dass Ausgaben in der Höhe von 90 · 20 = 1800 entstehen. Wie in Teilaufgabe (b) beträgt die aggregierte Produzentenrente 1350. Die
aggregierte Konsumentenrente ist nun
KR(10) = 90 · 90/2 = 4050.
5
Die Staatsausgaben wurden bereits als 1800 bestimmt, so dass die aggregierten
Handelsgewinne
HG = 1350 + 4050 − 1800 = 3600
betragen. Im Vergleich zum Wettbewerbsgleichgewicht werden die aggregierten
Handelsgewinne also um 150 Einheiten reduziert - die Handelsgewinne sind jedoch
um 400 Einheiten höher als in der Situation aus Teilaufgabe (b).
Abbildung 6: Grafische Darstellung zu Aufgabe 6 (c): Bei p̃ = 10 entspricht die nachgefragte
Menge der zum Preis p = 30 angebotenen Menge. Die Staatsausgaben entsprechen der
schraffierten Fläche.
7. Das Unternehmen sollte in den Markt eintreten, wenn sich dadurch ein Gewinn erzielen lässt. Ob dies der Fall ist, lässt sich wie folgt überprüfen: Man unterstellt zunächst,
das Unternehmen tritt in den Markt ein und bestimmt die in diesem Fall gewinnmaximierende Outputmenge und den resultierenden Gewinn. Ist dieser positiv, sollte das
Unternehmen eintreten. Ist der Gewinn negativ, sollte das Unternehmen dem Markt
fern bleiben.
Die Grenzkostenfunktion des aktiven Unternehmens ist durch M C(y) = 40 + 100y
gegeben und verläuft damit steigend. Ist das Unternehmen in den Markt eingetreten, ist die gewinnmaxierende Outputmenge also durch die Bedingung p = 40 + 100y
bestimmt. Mit p = 140 folgt hieraus y = 1. Der Gewinn bei dieser Outputmenge ist
140 − F − C(1) = 140 − 80 − 90 = −30
und somit negativ. Also sollte das Unternehmen nicht in den Markt eintreten.
Alternativer Lösungsansatz: Bestimme die minimalen Durchschnittskosten und
vergleiche sie mit dem Preis. Sind die minimalen Durchschnittskosten kleiner als der
6
Preis, sollte das Unternehmen eintreten. Anderenfalls sollte es inaktiv bleiben. Zur Bestimmung der minimalen Durchschnittskosten ist zunächst die effiziente Betriebsgrösse
ŷ zu bestimmen. Diese ist hier durch die Lösung des Problems
min AC(y) =
y≥0
80
+ 40 + 50y
y
gegeben. Die Bedingung erster Ordnung lautet:2
−
√
80
+ 50 = 0 ⇒ ŷ = 1.6.
ŷ 2
Die minimalen Durchschnittskosten sind also
√
80
AC(ŷ) = √
+ 40 + 50 1.6 ≈ 166.5
1.6
und liegen damit oberhalb des Preis p = 140. Wie zuvor ist die Schlussfolgerung, dass
das Unternehmen inaktiv bleiben sollte.
8. (a) Die Grenzkostenfunktion eines aktiven Unternehmens ist
M C(y) = 100 + 8y,
verläuft also streng steigend. Die Angebotsfunktion eines aktiven Unternehmens
ist also durch
0
für p < 100
s(p) =
(p − 100)/8 für p ≥ 100.
gegeben.
Sind m Unternehmen im Markt aktiv, so ist die Marktangebotsfunktion für p ≥
100 also durch
p − 100
Sm (p) = m
8
gegeben. Für p < 100 ist das Marktangebot gleich Null.
Der kurzfristige Wettbewerbspreis p∗m ist durch die Bedingung D(p∗m ) = Sm (p∗m )
bestimmt. Hier gilt also
1000 − p∗m = m
p∗m − 100
8000 + 100m
⇒ p∗m =
8
m+8
mit entsprechender Wettbewerbsmenge
∗
qm
= D(p∗m ) = 1000 − p∗m =
900m
.
m+8
(b) Um die Anzahl der Unternehmen zu bestimmen, die in einem langfristigen Wettbewerbsgleichgewicht aktiv sind, ist zuerst der langfristige Wettbewerbspreis zu
2 Anstatt
die Bedingung erster Ordnung herzuleiten, kann man auch direkt die Tatsache benutzen, dass die
effiziente Betriebsgrösse im Schnittpunkt von Grenzkostenfunktion und Durchschnittskostenfunktion liegt,
also durch die Gleichung
80
M C(ŷ) = AC(ŷ) ⇔ 100y =
+ 50y
y
gegeben ist.
7
Abbildung 7: Marktnachfragefunktion und kurzfristige Marktangebotsfunktionen für m =
20, m = 50 und m = 100 zu Aufgabe 8 (a). Kurzfristiger Wettbewerbspreis und Wettbewerbsmenge liegen in dem jeweiligen Schnittpunkt der kurzfristigen Marktangebotsfunktionen mit der Marktnachfragefunktion.
bestimmen. Dieser ist durch das Minimum der Durchschnittskosten gegeben. Das
entsprechende Minimierungsproblem3 ist
min
y>0
100
+ 100 + 4y
y
mit Bedingung erster Ordnung
−
100
+ 4 = 0 ⇒ 4y 2 = 100 ⇒ y = 5.
y2
Die Menge, bei der die Durchschnittskosten minimiert werden, ist also ŷ = 5.
Setzt man diese Menge in die Durchschnittskostenfunktion ein, erhält man den
langfristigen Wettbewerbspreis:
p∗ =
100
+ 100 + 4 · 5 = 140.
5
Die Marktnachfrage zu diesem Preis bestimmt die langfristige Wettbewerbsmenge
als q ∗ = D(140) = 860. Da jedes Unternehmen im Markt zu diesem Preis die
Menge ŷ = s(140) = 5 anbietet und im Gleichgewicht die angebotene Menge mit
der nachgefragten Menge übereinstimmt, muss
860 = m∗ 5 ⇒ m∗ = 172
gelten. Die Anzahl der Unternehmen, die in einem langfristigen Wettbewerbsgleichgewicht in diesem Markt aktiv sind, ist also 172.
3 Die
Beobachtung aus der vorhergehenden Fussnote gilt hier entsprechend.
8
Abbildung 8: Zu Aufgabe 8 (b): Der kurzfristige Wettbewerbspreis als Funktion der Anzahl
der aktiven Unternehmen in Relation zu den minimalen Durchschnittskosten: Für m <
172 liegt der Wettbewerbspreis oberhalb von min AC(y), so dass die aktiven Unternehmen
streng positive Gewinne erzielen und sich der Marktzutritt für inaktive Unternehmen lohnt.
Für m > 172 liegt der Wettbewerbspreis unterhalb von min AC(y), so dass die aktiven
Unternehmen Verluste erleiden und sich daher der Marktaustritt lohnt.
(c) Die Kostenfunktion eines aktiven Unternehmens ist nun durch
C(y) = 400 + 100y + 4y 2
gegeben. Die Durchschnittskosten sind entsprechend
AC(y) =
400
+ 100 + 4y
y
und werden bei der effizienten Betriebsgrösse ŷ = 10 minimiert. Die dazugehörigen
minimalen Durchschnittskosten sind p∗ = 180. Der langfristige Wettbewerbspreis
steigt auf Grund der Gebühr also von 140 auf 180 an. Da D(180) = 820 ist, fällt
die langfristige Wettbewerbsmenge von 860 auf q ∗ = 820. Die Anzahl der aktiven
Unternehmen fällt von 172 auf m∗ = 82 = 820/10.
9. In einem langfristigen Wettbewerbsgleichgewicht erzielen alle aktiven Unternehmen
Nullgewinne. Ihre kurzfristigen Fixkosten müssen also mit ihrer kurzfristigen Produzentenrente übereinstimmen. Diese Beobachtung ermöglicht es, die Aufgabe auch ohne
Herleitung der Kostenfunktion zu lösen, da sich die kurzfristige Produzentenrente direkt aus der Angebotsfunktion eines aktiven Unternehmens als p2 /2 bestimmen lässt.
Der langfristige Wettbewerbspreis ist also durch die Gleichung 2 = p2 /2 als p∗ = 2 bestimmt. Bei diesem Preis ist die Marktnachfrage gleich 8. Da jedes aktive Unternehmen
bei p∗ = 2 die Menge 2 anbietet, folgt dass es im langfristigen Wettbewerbsgleichgewicht 4 aktive Unternehmen gibt.
Alternativer Lösungsweg: Da die Angebotsfunktion streng steigend und stetig ist,
stimmt die inverse Angebotsfunktion mit der Grenzkostenfunktion überein. Also ist
die Grenzkostenfunktion eines aktiven Unternehmens durch M C(y) = y gegeben. Da
9
die Fläche unter den Grenzkosten den variablen Kosten entspricht, ist die Kostenfunktion eines aktiven Unternehmens durch C(y) = 2 + 0.5y 2 gegeben. Die dazugehörigen
Durchschnittskosten sind AC(y) = 2/y + 0.5y und werden bei ŷ = 2 minimiert. Da
AC(ŷ) = 2 ist der langfristige Wettbewerbspreis p∗ = 2. Der Rest des Arguments ist
wie zuvor.
10